Skip to main content
Global

14.6: Kanuni ya Archimedes na Buoyancy

  1. Last updated
  2. Save as PDF
  • Page ID
    177037

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Kufafanua nguvu ya buoyant
    • Kanuni ya Serikali ya Archimedes
    • Eleza uhusiano kati ya wiani na kanuni ya Archimedes

    Wakati kuwekwa kwenye maji, vitu vingine vinaelea kutokana na nguvu ya buoyant. Nguvu hii ya buoyant inatoka wapi? Kwa nini ni kwamba baadhi ya mambo kuelea na wengine hawana? Je! Vitu vinavyozama hupata msaada wowote kutoka kwenye maji? Je! Mwili wako umejaa anga, au ni balloons ya heliamu tu walioathirika (Kielelezo\(\PageIndex{1}\))?

    Kielelezo A ni kuchora ya nanga ya meli iliyokuwa chini ya maji karibu na baadhi ya vichaka bahari. Kielelezo B ni picha ya manowari inayozunguka na kuamka pande tatu. Kielelezo C ni picha ya balloons nyingi za rangi zinazozunguka hewa.
    Kielelezo\(\PageIndex{1}\): (a) Hata vitu vinavyozama, kama nanga hii, vinasaidiwa na maji wakati wa kuzama. (b) Submarines na wiani adjustable (mizinga ballast) ili waweze kuelea au kuzama kama taka. (c) Balloons iliyojaa Heliamu hupanda juu ya masharti yao, na kuonyesha athari ya hewa ya buoyant. (mikopo b: mabadiliko ya kazi na Allied Navy; mikopo c: mabadiliko ya kazi na “Crystl” /Flickr)

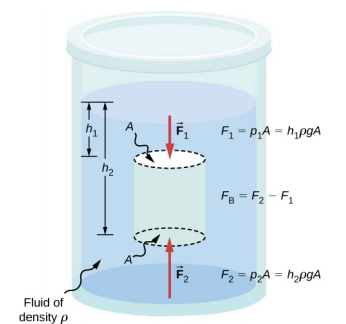
    Majibu ya maswali haya yote, na wengine wengi, yanategemea ukweli kwamba shinikizo huongezeka kwa kina katika maji. Hii ina maana kwamba nguvu ya juu chini ya kitu katika maji ni kubwa kuliko nguvu ya kushuka juu ya kitu. Kuna nguvu ya juu, au nguvu ya buoyant, juu ya kitu chochote katika maji yoyote (Kielelezo\(\PageIndex{2}\)). Ikiwa nguvu ya buoyant ni kubwa kuliko uzito wa kitu, kitu kinaongezeka kwenye uso na kinaelea. Ikiwa nguvu ya buoyant ni chini ya uzito wa kitu, kitu kinazama. Ikiwa nguvu ya buoyant inalingana na uzito wa kitu, kitu kinaweza kubaki kusimamishwa kwa kina chake cha sasa. Nguvu ya buoyant daima iko sasa, ikiwa kitu kinaelea, kinazama, au kinasimamishwa katika maji.

    Buoyant nguvu

    Nguvu ya buoyant ni nguvu ya juu juu ya kitu chochote katika maji yoyote.

    Kielelezo ni kuchora schematic ya silinda kujazwa na maji na kufunguliwa kwa anga upande mmoja. Kitu cha kufikiri na eneo la uso A, ambalo ni ndogo kuliko eneo la uso wa silinda, linaingia ndani ya maji. Umbali kati ya juu ya maji na juu ya kitu ni h1. Umbali kati ya juu ya maji na chini ya kitu ni h2. Vikosi vya F1 na F2 vinatumika juu na chini ya kitu, kwa mtiririko huo.
    Kielelezo\(\PageIndex{2}\): Shinikizo kutokana na uzito wa ongezeko la maji kwa kina kwa sababu\(p = h \rho g\). Mabadiliko haya katika shinikizo na kuhusishwa nguvu zaidi chini ya silinda ni kubwa kuliko nguvu kushuka juu ya silinda. Tofauti katika matokeo ya nguvu katika nguvu ya buoyant F B. (Vikosi vya usawa kufuta.)

    Kanuni ya Archimedes

    Jinsi nguvu kubwa ni nguvu ya buoyant? Ili kujibu swali hili, fikiria juu ya kile kinachotokea wakati kitu kilichojaa kimeondolewa kwenye maji, kama ilivyo kwenye Mchoro\(\PageIndex{3}\). Kama kitu hakuwa katika maji, nafasi kitu ulichukua itakuwa kujazwa na maji kuwa uzito w fl. Uzito huu unasaidiwa na maji ya jirani, hivyo nguvu ya buoyant lazima iwe sawa w fl, uzito wa maji yaliyohamishwa na kitu.

    Kanuni ya Archimedes

    Nguvu ya buoyant juu ya kitu ni sawa na uzito wa maji ambayo hutoka. Katika fomu ya equation, kanuni ya Archimedes ni

    \[F_{B} = w_{fl},\]

    ambapo F B ni nguvu ya buoyant na w fl ni uzito wa maji yaliyohamishwa na kitu.

    Kanuni hii inaitwa jina la mwanahisabati wa Kigiriki na mvumbuzi Archimedes (ca 287—212 KK), aliyesema kanuni hii muda mrefu kabla ya dhana za nguvu zilianzishwa vizuri.

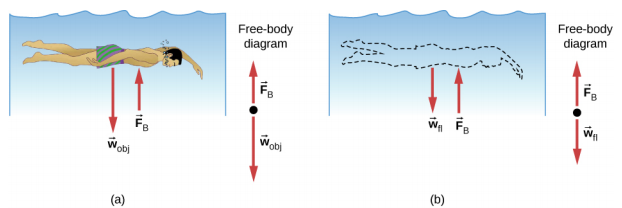
    Kielelezo A ni kuchora kwa mtu aliyeingia ndani ya maji. Nguvu wobj inaonyeshwa na mtu, nguvu Fb hutumiwa na maji kwa mtu. Kielelezo B ni kuchora ambayo mtu hubadilishwa na maji. Sasa Nguvu ya wfl inaonyeshwa na maji ambayo yamebadilisha mtu, nguvu Fb inabakia sawa.
    Kielelezo\(\PageIndex{3}\): (a) kitu kilichojaa katika uzoefu wa maji nguvu ya buoyant F B. Ikiwa F B ni kubwa kuliko uzito wa kitu, kitu kinaongezeka. Ikiwa F B ni chini ya uzito wa kitu, kitu kinazama. (b) Ikiwa kitu kinaondolewa, kinabadilishwa na maji yenye uzito w fl. Kwa kuwa uzito huu unasaidiwa na maji ya jirani, nguvu ya buoyant lazima iwe sawa na uzito wa maji yaliyohamishwa.

    Kanuni ya Archimedes inahusu nguvu ya buoyancy ambayo husababisha wakati mwili umejaa ndani ya maji, iwe sehemu au kabisa. Nguvu ambayo hutoa shinikizo la vitendo vya maji kwenye mwili perpendicular kwa uso wa mwili. Kwa maneno mengine, nguvu kutokana na shinikizo chini imeelezwa, wakati juu, nguvu kutokana na shinikizo imeelezwa; majeshi kutokana na shinikizo pande yanaelezea mwili.

    Kwa kuwa chini ya mwili ni kwa kina zaidi kuliko juu ya mwili, shinikizo kwenye sehemu ya chini ya mwili ni kubwa kuliko shinikizo kwenye sehemu ya juu, kama inavyoonekana kwenye Mchoro\(\PageIndex{2}\). Kwa hiyo nguvu ya juu ya wavu hufanya mwili. Nguvu hii ya juu ni nguvu ya buoyancy, au tu buoyancy.

    Mshangao wa “Eureka” (maana yake “Nimeipata”) mara nyingi umehesabiwa kwa Archimedes kama alivyofanya ugunduzi ambao utasababisha kanuni ya Archimedes. Wengine wanasema yote yalianza katika bafu. Kusoma hadithi, kuchunguza Scientific American kujifunza zaidi.

    Kanuni ya Wiani na Archimedes

    Ikiwa utaacha pua ya udongo ndani ya maji, itazama. Lakini ukitengeneza udongo huo wa udongo katika sura ya mashua, utaelea. Kwa sababu ya sura yake, mashua ya udongo huhamisha maji zaidi kuliko pua na hupata nguvu kubwa ya buoyant, ingawa umati wake ni sawa. Vile vile ni kweli kwa meli za chuma.

    Uzito wa wastani wa kitu ni nini hatimaye huamua kama inaelea. Ikiwa wiani wa kitu ni chini ya ule wa maji yaliyo karibu, itaelea. Sababu ni kwamba maji, yenye wiani mkubwa, ina wingi zaidi na hivyo uzito zaidi kwa kiasi sawa. Nguvu ya buoyant, ambayo inalingana na uzito wa maji yaliyohamishwa, hivyo ni kubwa kuliko uzito wa kitu. Vivyo hivyo, kitu denser kuliko maji kuzama.

    Kiwango ambacho kitu kinachozunguka kinaingia kinategemea jinsi wiani wa kitu unavyolingana na wiani wa maji. Katika Kielelezo\(\PageIndex{4}\), kwa mfano, meli iliyofunguliwa ina wiani wa chini na chini yake imejaa ikilinganishwa na meli hiyo wakati imefungwa. Tunaweza hupata kujieleza kiasi kwa sehemu iliyokuwa kwa kuzingatia wiani. Sehemu iliyojaa ni uwiano wa kiasi kilichojaa kwa kiasi cha kitu, au

    \[fraction\; submerged = \frac{V_{sub}}{V_{obj}} = \frac{V_{fl}}{V_{obj}} \ldotp\]

    Kiasi kilichojaa sawa na kiasi cha maji yaliyohamishwa, ambayo tunaita V fl. Sasa tunaweza kupata uhusiano kati ya densities kwa kubadili\(\rho = \frac{m}{V}\) katika kujieleza. Hii inakupa

    \[\frac{V_{fl}}{V_{obj}} = \frac{\frac{m_{fl}}{\rho_{fl}}}{\frac{m_{obj}}{\rho_{obj}}},\]

    ambapo\(\rho_{obj}\) ni wiani wastani wa kitu na\(\rho_{fl}\) ni wiani wa maji. Kwa kuwa kitu kinaelea, umati wake na ule wa maji yaliyohamishwa ni sawa, hivyo hufuta kutoka kwa usawa, wakiacha

    \[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}} \ldotp\]

    Tunaweza kutumia uhusiano huu kupima msongamano.

    Kielelezo A ni kuchora ya meli unloaded yaliyo juu katika maji. Kielelezo B ni kuchora kwa meli iliyobeba inayozunguka ndani ya maji.
    Kielelezo\(\PageIndex{4}\): Meli iliyofunguliwa (a) inaelea juu katika maji kuliko meli iliyobeba (b).
    Mfano 14.4: Kuhesabu Wastani wa Wastani

    Tuseme mwanamke wa kilo 60.0-anaelea katika maji safi na 97.0% ya kiasi chake kilichomwa wakati mapafu yake yamejaa hewa. Wiani wake wa wastani ni nini?

    Mkakati

    Tunaweza kupata wiani wa mwanamke kwa kutatua equation

    \[fraction\; submerged = \frac{\rho_{obj}}{\rho_{fl}}\]

    kwa wiani wa kitu. Hii mavuno

    \[\rho_{obj} = \rho_{person} = (fraction\; submerged) \cdotp \rho_{fl} \ldotp\]

    Tunajua sehemu zote zilizomo na wiani wa maji, hivyo tunaweza kuhesabu wiani wa mwanamke.

    Suluhisho

    Kuingia maadili inayojulikana katika kujieleza kwa wiani wake, tunapata

    \[\rho_{person} = 0.970 \cdotp 10^{3}\; kg/m^{3} = 970\; kg/m^{3} \ldotp\]

    Umuhimu

    Uzito wa mwanamke ni chini ya wiani wa maji. Tunatarajia hili kwa sababu yeye inaelea.

    Mbalimbali chini wiani vitu au vitu kuelea katika maji ya juu-wiani: mafuta juu ya maji, moto-hewa puto katika anga, kidogo ya cork katika mvinyo, barafu katika maji chumvi, na moto nta katika “taa lava,” kwa jina wachache. Mfano usio wazi ni safu za mlima zinazozunguka juu ya ukanda wa juu-wiani na vazi chini yao. Hata Dunia inayoonekana imara ina sifa za maji.

    Upimaji Wiani

    Moja ya mbinu za kawaida za kuamua wiani zinaonyeshwa kwenye Kielelezo\(\PageIndex{5}\).

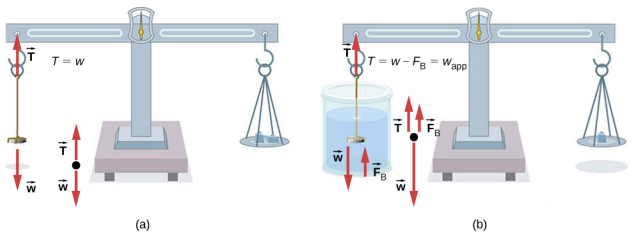
    Kielelezo A ni kuchora kwa sarafu katika hewa iliyopimwa kwa kiwango cha mwongozo. Uwiano mkubwa hutumiwa kusawazisha sarafu. Kielelezo B ni kuchora kwa sarafu moja katika maji iliyopimwa kwa kiwango cha mwongozo. Uwiano mdogo hutumiwa kusawazisha sarafu.
    Kielelezo\(\PageIndex{5}\): (a) Sarafu inapimwa hewa. (b) uzito dhahiri ya sarafu imedhamiria wakati ni kabisa iliyokuwa katika maji ya wiani inayojulikana. Vipimo hivi viwili hutumiwa kuhesabu wiani wa sarafu.

    Kitu, hapa sarafu, kinapimwa hewani na kisha kinapimwa tena huku kikiwa ndani ya kioevu. Uzito wa sarafu, dalili ya uhalali wake, unaweza kuhesabiwa kama wiani wa maji unajulikana. Tunaweza kutumia mbinu hiyo ili kuamua wiani wa maji kama wiani wa sarafu unajulikana.

    Mahesabu haya yote yanategemea kanuni ya Archimedes, ambayo inasema kwamba nguvu ya buoyant juu ya kitu ni sawa na uzito wa maji yaliyohamishwa. Hii, kwa upande wake, ina maana kwamba kitu kinaonekana kupima chini wakati umejaa; tunaita kipimo hiki uzito wa kitu kinachoonekana. Kitu kinakabiliwa na kupoteza uzito dhahiri sawa na uzito wa maji yaliyohamishwa. Vinginevyo, kwa mizani ambayo hupima wingi, kitu kinakabiliwa na kupoteza kwa wingi sawa na wingi wa maji yaliyohamishwa. Hiyo ni, dhahiri kupoteza uzito sawa na uzito wa maji makazi yao, au dhahiri molekuli hasara sawa wingi wa maji makazi yao.