14.5: Kanuni ya Pascal na Hydraulics

Last updated
Save as PDF

Page ID: 177036

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kanuni ya hali ya Pascal
Eleza matumizi ya kanuni ya Pascal
Kupata uhusiano kati ya vikosi katika mfumo wa majimaji

Mwaka 1653, mwanafalsafa wa Kifaransa na mwanasayansi Blaise Pascal alichapisha Treatise yake juu ya Msawazo wa Liquids, ambako alijadili kanuni za maji ya tuli. Maji ya tuli ni maji yasiyo na mwendo. Wakati maji hayapita, tunasema kwamba maji yana katika usawa wa tuli. Ikiwa maji ni maji, tunasema ni katika usawa wa hydrostatic. Kwa maji katika usawa wa tuli, nguvu ya wavu kwenye sehemu yoyote ya maji lazima iwe sifuri; vinginevyo maji yataanza kuzunguka.

Uchunguzi wa Pascal-tangu kuthibitishwa kijaribio-hutoa msingi wa majimaji, mojawapo ya maendeleo muhimu zaidi katika teknolojia ya kisasa ya mitambo. Pascal aliona kuwa mabadiliko katika shinikizo yanayotumiwa kwenye maji yaliyofungwa yanaambukizwa bila kupunguzwa katika maji na kuta za chombo chake. Kwa sababu hii, mara nyingi tunajua zaidi juu ya shinikizo kuliko kiasi kingine cha kimwili katika maji. Aidha, kanuni ya Pascal ina maana kwamba shinikizo la jumla katika maji ni jumla ya shinikizo kutoka vyanzo tofauti. Mfano mzuri ni maji kwa kina hutegemea kina cha maji na shinikizo la angahewa.

Kanuni ya Pascal

Kanuni ya Pascal (pia inajulikana kama sheria ya Pascal) inasema kwamba wakati mabadiliko ya shinikizo yanatumiwa kwenye maji yaliyofungwa, hupitishwa bila kupunguzwa kwa sehemu zote za maji na kuta za chombo chake. Katika maji yaliyofungwa, kwa kuwa atomi za maji ni huru kuhamia, zinatumia shinikizo kwa sehemu zote za maji na kuta za chombo. Mabadiliko yoyote katika shinikizo yanaambukizwa bila kupunguzwa.

Kumbuka kuwa kanuni hii haisemi kwamba shinikizo ni sawa katika sehemu zote za kiowezi—ambayo si kweli, kwani shinikizo katika maji karibu na Dunia hutofautiana na urefu. Badala yake, kanuni hii inatumika kwa mabadiliko katika shinikizo. Tuseme unaweka maji katika chombo cha cylindrical cha urefu H na eneo la msalaba A ambalo lina pistoni inayohamishika ya molekuli m (Kielelezo\(\PageIndex{1}\)). Kuongeza uzito Mg juu ya pistoni huongeza shinikizo juu na\(\frac{Mg}{A}\), tangu uzito wa ziada pia hufanya juu ya eneo A la kifuniko:

\[\Delta p_{top} = \frac{Mg}{A} \ldotp\]

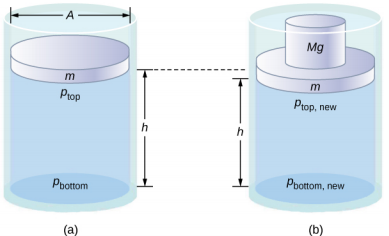
Kielelezo A ni kuchora schematic ya silinda iliyojaa maji na kufunguliwa kwa anga upande mmoja. Disk ya molekuli m na eneo la uso A sawa na eneo la uso wa silinda linawekwa kwenye chombo. Umbali kati ya disk na chini ya silinda ni h Kielelezo B ni kuchora schematic ya silinda na disk ya ziada ya molekuli Mg kuwekwa atop molekuli m kusababisha molekuli m kuhamia chini. — Kielelezo\(\PageIndex{1}\): Shinikizo katika mabadiliko ya maji wakati maji yanasisitizwa. (a) Shinikizo kwenye safu ya juu ya maji ni tofauti na shinikizo kwenye safu ya chini. (b) Kuongezeka kwa shinikizo kwa kuongeza uzito kwa pistoni ni sawa kila mahali, kwa mfano, p _juu _mpya - p _juu = p _chini _mpya - p _chini.

Kwa mujibu wa kanuni ya Pascal, shinikizo wakati wote katika maji hubadilika kwa kiasi sawa,\(\frac{Mg}{A}\). Hivyo, shinikizo chini pia huongezeka kwa\(\frac{Mg}{A}\). Shinikizo chini ya chombo ni sawa na jumla ya shinikizo la anga, shinikizo kutokana na maji, na shinikizo hutolewa na wingi. Mabadiliko katika shinikizo chini ya chombo kutokana na wingi ni

\[\Delta p_{bottom} = \frac{Mg}{A} \ldotp\]

Kwa kuwa mabadiliko ya shinikizo ni sawa kila mahali katika maji, hatuhitaji tena usajili ili kutaja mabadiliko ya shinikizo kwa juu au chini:

\[\Delta p = \Delta p_{top} = \Delta p_{bottom} = \Delta p_{everywhere} \ldotp\]

Masimulizi

Pascal ya Barrel ni maandamano makubwa ya kanuni ya Pascal. Tazama simulation ya jaribio la Pascal la 1646, ambalo alionyesha madhara ya kubadilisha shinikizo katika maji.

Matumizi ya Kanuni ya Pascal na Mifumo ya Hydraulic

Mifumo ya majimaji hutumiwa kuendesha breki za magari, vifungo vya majimaji, na mifumo mingine mingi ya mitambo (Kielelezo\(\PageIndex{2}\)).

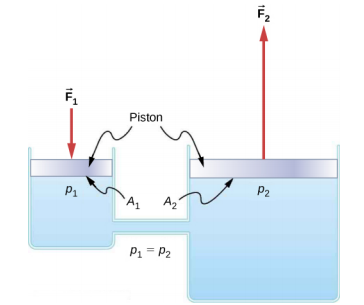
Mchoro wa schematic wa mfumo wa majimaji na mitungi miwili iliyojaa maji, imefungwa na pistoni na kushikamana na tube. Nguvu ya chini F1 kwenye pistoni ya kushoto na eneo la uso A1 inajenga mabadiliko katika shinikizo ambalo husababisha nguvu ya juu F2kwenye pistoni sahihi na eneo la uso A2. Eneo la uso A2 ni kubwa kuliko eneo la uso A1. — Kielelezo\(\PageIndex{2}\): Mfumo wa majimaji ya kawaida na mitungi miwili iliyojaa maji, imefungwa na pistoni na kushikamana na tube inayoitwa mstari wa majimaji. Nguvu ya kushuka\(\vec{F}_{1}\) kwenye pistoni ya kushoto inajenga mabadiliko katika shinikizo ambalo hupitishwa bila kupunguzwa kwa sehemu zote za maji yaliyofungwa. Hii inasababisha nguvu zaidi\(\vec{F}_{2}\) kwenye pistoni sahihi ambayo ni kubwa kuliko\(\vec{F}_{1}\) kwa sababu pistoni sahihi ina eneo kubwa la uso.

Tunaweza kupata uhusiano kati ya majeshi katika mfumo huu rahisi wa majimaji kwa kutumia kanuni ya Pascal. Kumbuka kwanza kwamba pistoni mbili katika mfumo zina urefu sawa, kwa hiyo hakuna tofauti katika shinikizo kutokana na tofauti kwa kina. Shinikizo kutokana na F ₁ inayofanya eneo A ₁ ni tu

\(p_{1} = \frac{F_{1}}{A_{1}}\), kama inavyoelezwa na\(p = \frac{F}{A}\).

Kwa mujibu wa kanuni ya Pascal, shinikizo hili linatumiwa bila kupunguzwa katika maji na kuta zote za chombo. Hivyo, shinikizo p ₂ linaonekana kwenye pistoni nyingine ambayo ni sawa na p ₁. Hiyo ni, p ₁ = p ₂. Hata hivyo, tangu p ₂ =\(\frac{F_{2}}{A_{2}}\), tunaona hiyo

\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp \label{14.12}\]

Equation hii inahusiana uwiano wa nguvu na eneo katika mfumo wowote wa majimaji, isipokuwa kwamba pistoni ni katika urefu sawa wima na kwamba msuguano katika mfumo ni duni.

Mifumo ya majimaji inaweza kuongeza au kupunguza nguvu iliyotumiwa kwao. Ili kufanya nguvu kubwa, shinikizo hutumiwa kwenye eneo kubwa. Kwa mfano, kama silinda kushoto kutumika 100-N nguvu katika Kielelezo 14.16 na silinda haki ina eneo la mara tano zaidi, pato nguvu 500 N. mifumo ya majimaji ni sawa na levers rahisi, lakini wana faida kwamba shinikizo inaweza kutumwa kwa njia ya mistari tortuously ikiwa na kadhaa maeneo kwa mara moja.

Jack ya majimaji ni mfumo wa majimaji. Jack ya majimaji hutumiwa kuinua mizigo nzito, kama vile ile inayotumiwa na mitambo ya magari ili kuongeza gari. Inajumuisha maji yasiyotumiwa katika tube ya U iliyofungwa na pistoni inayohamishika kila upande. Sehemu moja ya U-tube ni nyembamba kuliko nyingine. Nguvu ndogo inayotumiwa juu ya eneo ndogo inaweza kusawazisha nguvu kubwa zaidi upande mwingine juu ya eneo kubwa (Kielelezo\(\PageIndex{3}\)).

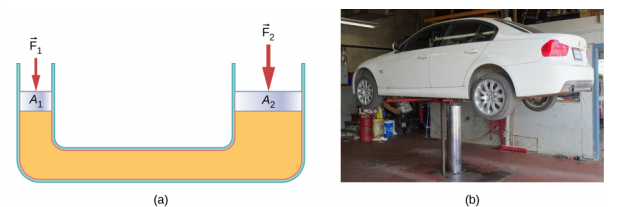
Kielelezo A ni kuchora schematic ya tube U kujazwa na maji. Nguvu ya chini F1 inatumika upande wa kushoto na eneo la uso A1. Nguvu ya chini F2 inatumika upande wa kulia na eneo la uso A2. Eneo la uso A2 ni kubwa kuliko eneo la uso A1.Kielelezo B ni picha ya gari la abiria lililowekwa kwenye jack ya majimaji. — Kielelezo\(\PageIndex{3}\): (a) Jack hydraulic kazi kwa kutumia nguvu (F ₁, F ₂) kwa maji incompressible katika U-tube, kwa kutumia piston zinazohamishika (A ₁, A ₂) kila upande wa tube. (b) Jacks za majimaji hutumiwa kwa kawaida na mitambo ya gari ili kuinua magari ili matengenezo na matengenezo yaweze kufanywa.

Kutoka kanuni ya Pascal, inaweza kuonyeshwa kuwa nguvu inahitajika kuinua gari ni chini ya uzito wa gari:

\[F_{1} = \frac{A_{1}}{A_{2}} F_{2},\]

ambapo F ₁ ni nguvu inayotumika kuinua gari, A ₁ ni eneo la msalaba wa pistoni ndogo, A ₂ ni eneo la msalaba wa pistoni kubwa, na F ₂ ni uzito wa gari.

Mfano\(\PageIndex{1}\): Calculating Force on Wheel Cylinders: Pascal Puts on the Brakes

Fikiria mfumo wa majimaji ya magari umeonyeshwa kwenye Kielelezo\(\PageIndex{4}\). Tuseme nguvu ya 100 N inatumika kwa pedal iliyovunja, ambayo hufanya silinda ya pedal (kutenda kama silinda “bwana”) kupitia lever. Nguvu ya 500 N inatumiwa kwenye silinda ya pedal. Shinikizo lililoundwa katika silinda ya pedal linapitishwa kwenye mitungi minne ya gurudumu Silinda ya kanyagio ina kipenyo cha sentimita 0.500 na kila silinda ya gurudumu ina kipenyo cha sentimita 2.50. Tumia ukubwa wa nguvu F ₂ iliyoundwa katika kila mitungi ya gurudumu.

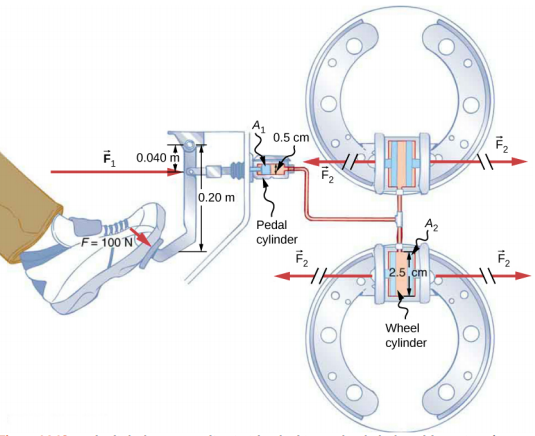
Kielelezo ni kuchora schematic ya mfumo wa kuvunja majimaji. Mguu hutumiwa kwenye kanyagio la kuvunja na nguvu F1. Inapitishwa kwenye silinda ya pedal na eneo la A1 la cm 0.5. Silinda ya Pedal imeshikamana na mfumo wa majimaji na mitungi miwili ya gurudumu na eneo la A2 la cm 2.5. Wheel mitungi kujenga pato nguvu F2. — Kielelezo\(\PageIndex{4}\): Breki za majimaji hutumia kanuni ya Pascal. Dereva hupiga kanyagio la kuvunja, akitumia nguvu inayoongezeka kwa lever rahisi na tena kwa mfumo wa majimaji. Kila moja ya mitungi ya gurudumu inayofanana inapata shinikizo sawa na, kwa hiyo, hujenga pato sawa la nguvu F ₂. Sehemu za mviringo za mviringo za mitungi ya pedal na gurudumu zinawakilishwa na A ₁ na A ₂, kwa mtiririko huo

Mkakati

Tunapewa nguvu F ₁ iliyotumiwa kwenye silinda ya pedal. Sehemu za msalaba A ₁ na A ₂ zinaweza kuhesabiwa kutoka kwa kipenyo chao kilichopewa. Kisha tunaweza kutumia uhusiano wafuatayo ili kupata nguvu F ₂:

\[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp\]

Kuendesha hii algebraically kupata F ₂ upande mmoja na mbadala inayojulikana maadili.

Suluhisho

Kanuni ya Pascal inayotumika kwa mifumo ya majimaji hutolewa na\(\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}}\):

\[\begin{split} F_{2} & = \frac{A_{2}}{A_{1}} F_{1} = \frac{\pi r_{2}^{2}}{\pi r_{1}^{2}} F_{1} \\ & = \frac{(1.25\; cm)^{2}}{(0.250\; cm)^{2}} \times 500\; N = 1.25 \times 10^{4}\; N \ldotp \end{split}\]

Umuhimu

Thamani hii ni nguvu inayotumiwa na kila moja ya mitungi minne ya gurudumu. Kumbuka kwamba tunaweza kuongeza mitungi wengi gurudumu kama tunataka. Ikiwa kila mmoja ana kipenyo cha sentimita 2.50, kila mmoja atafanya 1.25 x 10 ⁴ N. mfumo rahisi wa majimaji, kama mfano wa mashine rahisi, unaweza kuongeza nguvu lakini hauwezi kufanya kazi zaidi kuliko ilivyofanyika juu yake. Kazi ni nguvu mara umbali wakiongozwa, na silinda gurudumu hatua kwa njia ya umbali ndogo kuliko silinda kanyagio. Zaidi ya hayo, magurudumu zaidi aliongeza, ndogo umbali kila hatua moja. Mifumo mingi ya majimaji - kama vile breki za nguvu na zile zilizo katika bulldozers-zina pampu ya motorized ambayo kwa kweli inafanya kazi nyingi katika mfumo.

Zoezi\(\PageIndex{1}\)

Je, vyombo vya habari vya majimaji bado vinatumika vizuri ikiwa gesi inatumiwa badala ya kioevu?