13.6: Sheria za Kepler za Mwendo wa Sayari

Last updated
Save as PDF

Page ID: 176746

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Eleza sehemu za conic na jinsi zinahusiana na mwendo wa orbital
Eleza jinsi kasi ya orbital inahusiana na uhifadhi wa kasi ya angular
Kuamua kipindi cha obiti ya elliptical kutoka kwa mhimili wake mkuu

Kwa kutumia data sahihi zilizokusanywa na Tycho Brahe, Johannes Kepler alichambua kwa makini nafasi za anga za sayari zote zinazojulikana na Mwezi, akipanga nafasi zao kwa vipindi vya mara kwa mara. Kutokana na uchambuzi huu, aliandaa sheria tatu, ambazo tunazungumzia katika sehemu hii.

Sheria ya Kwanza ya Kepler

Mtazamo uliopo wakati wa Kepler ulikuwa kwamba njia zote za sayari zilikuwa za mviringo. Takwimu za Mars ziliwasilisha changamoto kubwa kwa mtazamo huu na kwamba hatimaye ilimhimiza Kepler kuacha wazo maarufu. Sheria ya kwanza ya Kepler inasema kwamba kila sayari inakwenda pamoja na duaradufu, huku Jua liko kwenye lengo la duaradufu. ellipse hufafanuliwa kama seti ya pointi zote kama kwamba jumla ya umbali kutoka kila hatua hadi foci mbili ni mara kwa mara. Kielelezo\(\PageIndex{1}\) kinaonyesha ellipse na inaelezea njia rahisi ya kuunda.

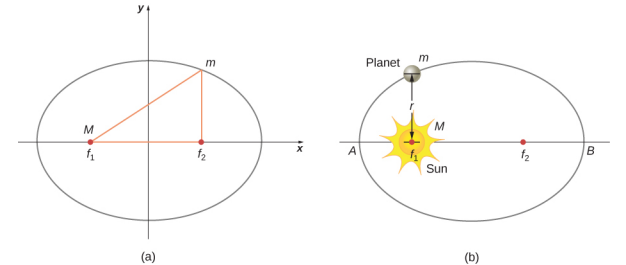
Kielelezo a inaonyesha mfumo wa kuratibu x y na duaradufu unaozingatia asili na foci f 1 upande wa kushoto na f 2 upande wa kulia, wote kwenye mhimili x. Focus f 1 pia kinachoitwa M. uhakika juu ya lengo f 2 ni kinachoitwa m. pembetatu haki sumu na f 1, f 2, na m ni inavyoonekana katika nyekundu. Kielelezo b inaonyesha duaradufu sawa, na jua inavyoonekana na kinachoitwa kama M na kama Sun katika f 1. Masi ya sayari m inavyoonyeshwa hapo juu f 1, kwa umbali wa wima r kutoka f 1. Eneo ambapo duaradufu inakabiliana na mhimili usawa upande wa kushoto inaitwa kama hatua A, na mahali ambapo duaradufu huingilia mhimili usawa upande wa kulia ni kinachoitwa kama hatua B. — Kielelezo\(\PageIndex{1}\): (a) duaradufu ni pembe ambayo jumla ya umbali kutoka hatua kwenye pembe hadi foci mbili (f ₁ na f ₂) ni mara kwa mara. Kutoka kwa ufafanuzi huu, unaweza kuona kwamba ellipse inaweza kuundwa kwa njia ifuatayo. Weka siri katika kila lengo, kisha uweke kitanzi cha kamba karibu na penseli na pini. Kuweka kamba kufundishwa, hoja penseli kuzunguka katika mzunguko kamili. Ikiwa foci mbili zinachukua sehemu moja, matokeo ni mduara-kesi maalum ya duaradufu. (b) Kwa obiti ya duaradufu, ikiwa m <<<M, basi m inafuata njia ya elliptical na M kwa lengo moja. Zaidi zaidi, wote m na M huhamia katika ellipse yao wenyewe kuhusu kituo cha kawaida cha wingi.

Kwa njia za elliptical, hatua ya mbinu ya karibu ya sayari hadi Jua inaitwa perihelion. Ni kinachoitwa hatua A katika Kielelezo\(\PageIndex{1}\). Hatua ya mbali ni aphelion na inaitwa hatua B katika takwimu. Kwa obiti ya Mwezi kuhusu Dunia, pointi hizo huitwa perigee na apogee, kwa mtiririko huo.

duaradufu ina aina kadhaa hisabati, lakini wote ni kesi maalum ya equation zaidi ya jumla kwa sehemu conic. Kuna sehemu nne tofauti za conic, zote zinazotolewa na equation

\[\frac{\alpha}{r} = 1 + e \cos \theta \ldotp \label{13.10}\]

vigezo\(r\) na\(\theta\) ni inavyoonekana katika Kielelezo\(\PageIndex{2}\) katika kesi ya duaradufu. Vipindi α na e vinatambuliwa na nishati ya jumla na kasi ya angular ya satellite kwa hatua fulani. Mara kwa mara e inaitwa eccentricity. Maadili ya\(\alpha\) na e kuamua ni sehemu gani ya nne za conic inawakilisha njia ya satellite.

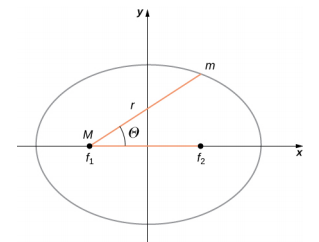
Mfumo wa kuratibu x y na duaradufu unaozingatia asili na foci f 1 upande wa kushoto na f 2 upande wa kulia, wote kwenye mhimili wa x, huonyeshwa. Focus f 1 pia inaitwa M. uhakika juu ya duaradufu katika roboduara ya kwanza ni kinachoitwa m. sehemu ya usawa kuunganisha foci f 1 na f 2, na sehemu ya kuunganisha f 1 na m inavyoonekana katika nyekundu. Pembe kati ya makundi hayo ni kinachoitwa Theta. — Kielelezo\(\PageIndex{2}\): Kama hapo awali, umbali kati ya sayari na jua ni\(r\), na angle kipimo kutoka x-axis, ambayo ni pamoja na mhimili mkubwa wa duaradufu, ni\(\theta\).

Moja ya ushindi halisi wa sheria ya Newton ya gravitation zima, na nguvu sawia na inverse ya umbali squared, ni kwamba wakati ni pamoja na sheria yake ya pili, ufumbuzi kwa njia ya satellite yoyote ni sehemu conic. Kila njia iliyochukuliwa na m ni moja ya sehemu nne za conic: mduara au duaradufu kwa njia zilizofungwa au zilizofungwa, au parabola au hyperbola kwa njia zisizo na mipaka au wazi. Sehemu hizi za conic zinaonyeshwa kwenye Kielelezo\(\PageIndex{3}\).

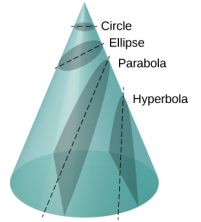
Koni na sehemu zake za conic zinaonyeshwa. Juu kukata usawa ni kivuli na mstari uliopigwa umeonyeshwa kwenye shading. Sehemu hii ni lebo mduara. Chini ya hii kukata diagonal na mstari huonyeshwa. Mstari na kukata huingiliana pande za koni. Sehemu hii imeandikwa ellipse. Ifuatayo ni kukata diagonal na mstari unaoingiliana pande na chini ya koni na ni kinachoitwa parabola. Sehemu ya mwisho ni mstari wa wima na kivuli kilichokatwa kinachoitwa hyperbola — Kielelezo\(\PageIndex{3}\): Mwendo wote unaosababishwa na nguvu ya mraba inverse ni moja ya sehemu nne za conic na imedhamiriwa na nishati na mwelekeo wa mwili unaohamia

Ikiwa nishati ya jumla ni hasi, basi 0 ≤ e <1, na Equation\ ref {13.10} inawakilisha obiti iliyofungwa au imefungwa ya ama duaradufu au mduara, ambapo e = 0. [Unaweza kuona kutoka Equation 13.10 kwamba kwa e = 0, r =\(\alpha\), na hivyo radius ni mara kwa mara.] Kwa ellipses, eccentricity ni kuhusiana na jinsi mviringo mviringo inaonekana. Mduara una usawa wa sifuri, wakati ellipse ndefu sana, inayotolewa nje ina eccentricity karibu na moja.

Ikiwa nishati ya jumla ni sifuri, basi e = 1 na njia ni parabola. Kumbuka kwamba satellite yenye nishati ya jumla ya sifuri ina kasi ya kutoroka. (Parabola hutengenezwa tu kwa kupiga koni sambamba na mstari wa tangent kando ya uso.) Hatimaye, ikiwa nishati ya jumla ni chanya, basi e> 1 na njia ni hyperbola. Njia hizi mbili za mwisho zinawakilisha njia zisizo na mipaka, ambapo m hupita kwa M mara moja na mara moja tu. Hali hii imezingatiwa kwa comets kadhaa ambazo zinakaribia jua na kisha kusafiri mbali, kamwe kurudi.

Sisi funge wenyewe kwa kesi ambayo molekuli ndogo (sayari) huzunguka kubwa zaidi, na hivyo stationary, wingi (Sun), lakini Equation 13.10 pia inatumika kwa raia yoyote mbili gravitationally kuingiliana. Kila molekuli athari nje halisi sawa-umbo sehemu conic kama nyingine. Sura hiyo imedhamiriwa na nishati ya jumla na kasi ya angular ya mfumo, na katikati ya wingi wa mfumo ulio kwenye lengo. Uwiano wa vipimo vya njia mbili ni inverse ya uwiano wa raia wao.

Masimulizi

Unaweza kuona uhuishaji wa vitu viwili vya kuingiliana kwenye ukurasa wangu wa Solar System kwenye Phet. Chagua chaguo la kupangilia Sun na Sayari. Unaweza pia kuona ngumu zaidi matatizo mbalimbali ya mwili kama vile. Unaweza kupata njia halisi ya Mwezi kushangaza kabisa, lakini ni kutii sheria rahisi za Newton za mwendo.

Orbital Transfers

Watu wamefikiri kusafiri kwenye sayari nyingine za mfumo wetu wa jua tangu ziligunduliwa. Lakini tunawezaje kufanya hivyo vizuri? Njia yenye ufanisi zaidi iligunduliwa mwaka wa 1925 na Walter Hohmann, iliyoongozwa na riwaya maarufu ya sayansi ya uongo wa wakati huo. Njia hii sasa inaitwa uhamisho wa Hohmann. Kwa kesi ya kusafiri kati ya njia mbili za mviringo, uhamisho ni pamoja na “uhamisho” wa ellipse ambayo inakataza kikamilifu njia hizo kwenye aphelion na perihelion ya duaradufu. Kielelezo\(\PageIndex{4}\) inaonyesha kesi kwa ajili ya safari kutoka obiti ya dunia na ile ya Mars. Kama hapo awali, Jua liko kwenye lengo la duaradufu.

Kwa duaradufu yoyote, mhimili wa nusu kuu hufafanuliwa kama nusu jumla ya perihelion na aphelion. Katika Kielelezo\(\PageIndex{4}\), mhimili wa nusu kuu ni umbali kutoka kwa asili hadi upande wowote wa duaradufu kando ya mhimili wa x-axis, au nusu moja tu ya mhimili mrefu (inayoitwa mhimili mkubwa). Kwa hiyo, kusafiri kutoka kwenye mzunguko mmoja wa mviringo wa radius r ₁ hadi mzunguko mwingine wa mviringo wa radius r ₂, aphelion ya duaradufu ya uhamisho itakuwa sawa na thamani ya obiti kubwa, wakati perihelion itakuwa obiti ndogo. Mhimili wa nusu kuu, uliotajwa, kwa hiyo hutolewa na\(a = \frac{1}{2} (r_{1} + r_{2})\).

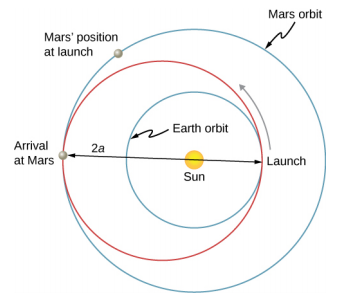
Mfano wa jua na njia tatu kuzunguka huonyeshwa. Njia zote tatu ni mviringo. Obiti ya ndani inazingatia jua na inaitwa Obiti ya Dunia. Obiti ya kati haijazingatia jua. Inafanana na obiti ya dunia kwenye hatua iliyoitwa “Uzinduzi” kwa haki ya jua. Mshale unaonyesha uzinduzi ni juu na kushoto. Kipenyo cha obiti kinaitwa kama umbali 2 a na huonyeshwa kutoka hatua ya uzinduzi upande wa kulia hadi hatua iliyoandikwa “Kuwasili Mars” upande wa kushoto. Jua liko juu ya kipenyo hiki. Obiti ya nje ni katikati ya jua na inaitwa Mars obiti. Obiti hii inafanana na obiti ya kati kwenye hatua iliyowekwa alama kama “Kuwasili Mars.” Hatua katika quadrant ya pili (iko saa moja kwa moja kutoka hatua ya kuwasili) inaitwa nafasi ya Mars wakati wa uzinduzi. — Kielelezo\(\PageIndex{4}\): Uhamisho duaradufu ina perihelion yake katika obiti ya dunia na aphelion katika obiti Mars '.

Hebu tuchukue kesi ya kusafiri kutoka Dunia hadi Mars. Kwa sasa, tunapuuza sayari na tunadhani tuko peke yake katika obiti ya Dunia na tunataka kuhamia kwenye obiti ya Mars. Kutoka Equation 13.9, kujieleza kwa jumla ya nishati, tunaweza kuona kwamba jumla ya nishati kwa spacecraft katika obiti kubwa (Mars) ni kubwa (chini hasi) kuliko ile kwa obiti ndogo (Dunia). Ili kuhamia kwenye duaradufu ya uhamisho kutoka kwenye obiti ya Dunia, tutahitaji kuongeza nishati yetu ya kinetic, yaani, tunahitaji kuongeza kasi. Njia yenye ufanisi zaidi ni kasi ya haraka sana kwenye njia ya mviringo ya mviringo, ambayo pia iko kwenye njia ya duaradufu wakati huo. (Kwa kweli, kuongeza kasi inapaswa kuwa instantaneous, kama vile mviringo na elliptical orbits ni congruent wakati wa kuongeza kasi. Katika mazoezi, kuongeza kasi ya mwisho ni ya kutosha kwamba tofauti sio kuzingatia muhimu.) Mara baada ya kufika katika obiti Mars, unahitaji mwingine kuongeza kasi ya kuhamia katika obiti kwamba, au wewe kukaa juu ya obiti elliptical na tu kuanguka nyuma perihelion ambapo ulianza. Kwa safari ya kurudi, unarudia tu mchakato na kuongeza retro katika kila hatua ya uhamisho.

Kufanya hoja kwenye duaradufu ya uhamisho na kisha tena, tunahitaji kujua kila kasi ya mzunguko wa mzunguko na kasi ya uhamisho wa obiti kwenye perihelion na aphelion. kuongeza kasi required ni tu tofauti kati ya mviringo obiti kasi na elliptical obiti kasi katika kila hatua. Tunaweza kupata mviringo orbital kasi kutoka Equation 13.7. Kuamua kasi kwa duaradufu, tunasema bila ushahidi (kama ilivyo zaidi ya upeo wa kozi hii) kwamba jumla ya nishati kwa obiti ya elliptical ni

\[E = - \frac{GmM_{S}}{2a}\]

ambapo M _S ni wingi wa Jua na a ni mhimili wa nusu-kuu. Kwa kushangaza, hii ni sawa na Equation 13.9 kwa njia za mviringo, lakini kwa thamani ya mhimili wa nusu kuu kuchukua nafasi ya radius orbital. Kwa kuwa tunajua nishati uwezo kutoka Equation 13.4, tunaweza kupata nishati kinetic na hivyo kasi zinahitajika kwa kila hatua juu ya duaradufu. Tunaiacha kama tatizo la changamoto ili kupata kasi hizo za uhamisho kwa safari ya Dunia-kwa-Mars.

Tunamaliza mjadala huu kwa kuonyesha maelezo machache muhimu. Kwanza, hatujahesabu nishati ya uwezo wa mvuto kutokana na Dunia na Mars, au mechanics ya kutua kwenye Mars. Katika mazoezi, hiyo lazima iwe sehemu ya mahesabu. Pili, muda ni kila kitu. Hutaki kufika kwenye obiti ya Mars ili kujua haipo. Lazima tuondoke Dunia kwa wakati sahihi kama vile Mars itakuwa katika aphelion ya ellipse yetu ya uhamisho kama sisi kufika. Nafasi hiyo inakuja kila baada ya miaka 2. Na kurudi inahitaji muda sahihi pia. Safari ya jumla itachukua chini ya miaka 3! Kuna chaguzi nyingine kwamba kutoa kwa ajili ya transit kasi, ikiwa ni pamoja na mvuto kusaidia flyby ya Venus. Lakini chaguzi hizi nyingine huja na gharama za ziada katika nishati na hatari kwa astronauts.

Kumbuka

Ziara tovuti hii (https://openstaxcollege.org/l/21plantripmars) kwa maelezo zaidi kuhusu mipango ya safari ya Mars.

Sheria ya Pili ya Kepler

Sheria ya pili ya Kepler inasema kwamba sayari inafuta maeneo sawa kwa nyakati sawa, yaani, eneo lililogawanyika kwa wakati, linaloitwa kasi ya areal, ni mara kwa mara. Fikiria Kielelezo\(\PageIndex{5}\). Wakati inachukua sayari kuhamia kutoka nafasi A hadi B, kuenea nje ya eneo A ₁, ni wakati hasa kuchukuliwa kuondoka kutoka nafasi C hadi D, yanayojitokeza eneo A ₂, na kuhamia kutoka E hadi F, kuenea nje eneo A ₃. Maeneo haya ni sawa: A ₁ = A ₂ = A ₃.

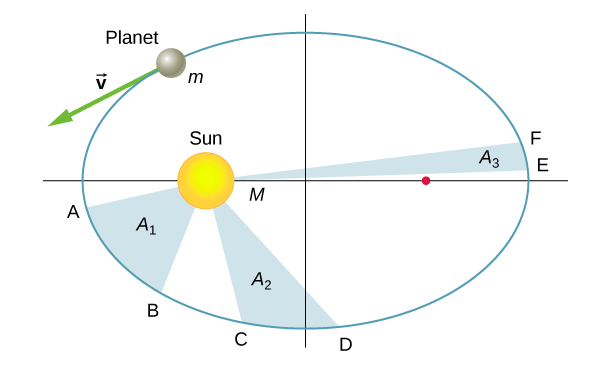
Mfumo wa kuratibu x y unaonyeshwa kwa jua, pia huitwa kama M, kwenye mhimili x upande wa kushoto wa asili na hatua isiyojulikana kwa haki ya asili. Sayari, iliyoandikwa pia kama m, inavyoonekana katika quadrant ya pili. mshale, kinachoitwa v, hadi kutoka sayari na pointi chini na kushoto, tangent kwa obiti. Pointi A, B, C, D, E, na F zimeandikwa kwenye obiti. Pointi A na B ziko katika roboduara ya tatu. Eneo la eneo lililofafanuliwa na A B na jua linaitwa A 1. Pointi C na D ziko kwenye obiti upande wowote wa mhimili — y. Eneo la eneo lililofafanuliwa na C D na jua linaitwa A 2. Pointi E na F ziko katika roboduara ya kwanza. Eneo la mkoa lililofafanuliwa na E F na jua linaitwa A 3. Vipande viwili vya A B vina umbali mkubwa kati yao na ni karibu zaidi na jua. E F ina umbali mdogo kati yao na ni mbali zaidi na jua. — Kielelezo\(\PageIndex{5}\): Mikoa ya kivuli iliyoonyeshwa ina maeneo sawa na inawakilisha muda huo huo.

Kulinganisha maeneo yaliyo kwenye takwimu na umbali uliotembea kando ya duaradufu katika kila kesi, tunaweza kuona kwamba ili maeneo yawe sawa, sayari lazima iharakishe inapokaribia Jua na kupunguza kasi inapoondoka. Tabia hii inafanana kabisa na equation yetu ya uhifadhi, Equation\ ref {13.5}. Lakini tutaonyesha kwamba sheria ya pili ya Kepler ni kweli matokeo ya uhifadhi wa kasi ya angular, ambayo inashikilia mfumo wowote wenye nguvu za radial tu.

Kumbuka ufafanuzi wa kasi ya angular kutoka kwa kasi ya Angular,\(\vec{L} = \vec{r} \times \vec{p}\). Kwa kesi ya mzunguko wa mwendo,\(\vec{L}\) ni kasi ya angular ya sayari kuhusu Jua,\(\vec{r}\) ni vector nafasi ya sayari kipimo kutoka Sun, na\(\vec{p}\) = m\(\vec{v}\) ni instantaneous linear kasi wakati wowote katika obiti. Tangu sayari hatua pamoja duaradufu,\(\vec{p}\) daima tangent kwa duaradufu.

Tunaweza kutatua kasi ya mstari katika vipengele viwili: sehemu ya radial\(\vec{p}_{rad}\) kando ya mstari hadi Jua, na sehemu ya\(\vec{p}_{perp}\) perpendicular kwa\(\vec{r}\). Bidhaa ya msalaba kwa kasi ya angular inaweza kuandikwa kama

\[\begin{align*} \vec{L} &= \vec{r} \times \vec{p} \\[4pt] &= \vec{r} \times (\vec{p}_{rad} + \vec{p}_{perp}) \\[4pt] &= \vec{r} \times \vec{p}_{rad} + \vec{r} \times \vec{p}_{perp} \ldotp \end{align*}\]

Neno la kwanza upande wa kulia ni sifuri kwa sababu\(\vec{r}\) ni sawa na\(\vec{p}_{rad}\), na katika kipindi cha pili\(\vec{r}\) ni perpendicular kwa\(\vec{p}_{perp}\), hivyo ukubwa wa bidhaa msalaba hupunguza

\[L = rp_{perp} = rmv_{perp}.\]

Kumbuka kuwa kasi ya angular haitegemei\(p_{rad}\). Kwa kuwa nguvu ya mvuto iko tu katika mwelekeo wa radial, inaweza kubadilika tu\(p_{rad}\) na sio\(p_{perp}\); kwa hiyo, kasi ya angular inapaswa kubaki mara kwa mara.

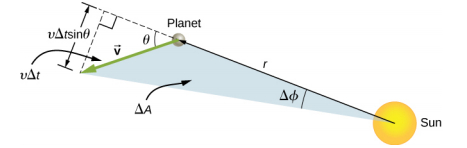
Mchoro kuonyesha jua na sayari kutengwa na r umbali. vector kasi ya sayari ni umeonyesha kama mshale akizungumzia katika angle obtuse kwa umbali r kati ya jua na sayari. line kuunganisha jua na sayari ni kupanuliwa nyuma sayari kama mstari dashed, na mstari mwingine dashed ni inayotolewa kutoka ncha ya mshale kasi kwa upanuzi dashed ya r. mistari dashed kukutana katika pembe ya kulia na kuunda pembetatu na mshale kasi kutengeneza hypotenuse na sayari kwa moja vertex. Pembe karibu na sayari inaitwa theta. hypotenuse pia kinachoitwa v delta t, na upande kinyume sayari kinachoitwa v delta t dhambi theta. Eneo la pembetatu lililofafanuliwa na jua, sayari na ncha ya mshale wa kasi huitwa Delta A, na angle karibu na jua inaitwa delta phi. — Kielelezo\(\PageIndex{6}\): Kipengele cha eneo\(\Delta\) A kilichotolewa kwa wakati\(\Delta\) t kama sayari inapita kupitia angle\(\Delta \phi\). Pembe kati ya mwelekeo wa radial na\(\vec{v}\) ni\(\theta\).

Sasa fikiria Kielelezo\(\PageIndex{6}\). Eneo ndogo la triangular\(\Delta A\) linatolewa kwa wakati\(\Delta t\). Kasi iko njiani na inafanya angle\(\theta\) na mwelekeo wa radial. Kwa hiyo, kasi ya perpendicular hutolewa na\(v_{perp}= v\sin \theta\). sayari hatua umbali\(\Delta\) s = v\(\Delta\) tsin\(\theta\) makadirio pamoja mwelekeo perpendicular kwa\(r\). Kwa kuwa eneo la pembetatu ni nusu ya msingi (\(r\)) mara urefu (\(\Delta s\)), kwa uhamisho mdogo, eneo hutolewa na

\[\Delta A = \frac{1}{2} r \Delta s. \nonumber\]

Kubadilisha\(\Delta s\), kuzidisha\(m\) kwa namba na denominator, na upya upya, tunapata

\[\Delta A = \frac{1}{2} r \Delta s = \frac{1}{2} r (v \Delta t \sin \theta) = \frac{1}{2m} r (mv \sin \theta \Delta t) = \frac{1}{2m} r (mv_{perp} \Delta t) = \frac{L}{2m} \Delta t \ldotp\]

kasi ya eneo ni tu kiwango cha mabadiliko ya eneo kwa wakati, hivyo tuna

\[ \text{areal velocity} = \frac{\Delta A}{\Delta t} = \frac{L}{2m} \ldotp\]

Kwa kuwa kasi ya angular ni mara kwa mara, kasi ya eneo lazima pia iwe mara kwa mara. Hii ni hasa sheria ya pili ya Kepler. Kama ilivyo kwa sheria ya kwanza ya Kepler, Newton alionyesha ilikuwa matokeo ya asili ya sheria yake ya mvuto.

Masimulizi

Unaweza kuona toleo animated ya Kielelezo\(\PageIndex{6}\), na mengine mengi ya mifano kwa michoro ya kuvutia kama vile, katika Shule ya Fizikia (Chuo Kikuu cha New South Wales) tovuti.

Sheria ya Tatu ya Kepler

Sheria ya tatu ya Kepler inasema ya kwamba mraba wa kipindi hicho ni sawia na mchemraba wa mhimili wa nusu-kuu wa obiti. Katika Orbits Satellite na Nishati, sisi inayotokana Kepler ya sheria ya tatu kwa ajili ya kesi maalum ya obiti mviringo. Equation\ ref {13.8} inatupa kipindi cha mzunguko wa mviringo wa radius r kuhusu Dunia:

\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.5.5}\]

Kwa ellipse, kumbuka kwamba mhimili wa nusu kuu ni nusu ya jumla ya perihelion na aphelion. Kwa obiti ya mviringo, mhimili wa nusu-kuu (\(a\)) ni sawa na radius kwa obiti. Kwa kweli, Equation\ ref {13.5.5} inatupa sheria ya tatu ya Kepler kama sisi tu kuchukua nafasi\(r\)\(a\) na mraba pande zote mbili.

\[T^{2} = \frac{4 \pi^{2}}{GM} a^{3} \label{13.11}\]

Tumebadilisha wingi wa Dunia kwa ujumla zaidi\(M\), tangu equation hii inatumika kwa satelaiti zinazozunguka molekuli yoyote kubwa.

Mfano\(\PageIndex{1}\): Orbit of Halley’s Comet

Tambua mhimili wa nusu-kuu wa obiti ya kimondo cha Halley, kutokana na kwamba unafika kwenye perihelion kila baada ya miaka 75.3. Ikiwa perihelion ni 0.586 AU, ni nini aphelion?

Mkakati

Tunapewa kipindi, ili tuweze kupanga upya Equation\ ref {13.11}, kutatua kwa mhimili wa nusu kuu. Kwa kuwa tunajua thamani ya perihelion, tunaweza kutumia ufafanuzi wa mhimili wa nusu kuu, iliyotolewa mapema katika sehemu hii, ili kupata aphelion. Tunaona kwamba 1 Unit Astronomical (AU) ni radius wastani wa obiti ya Dunia na hufafanuliwa kuwa 1 AU = 1.50 x 10 ¹¹ m.

Suluhisho

Kupanga upya Equation\ ref {13.11} na kuingiza maadili ya kipindi cha kimondo cha Halley na masi ya Jua, tuna

\[\begin{split} a & = \left(\dfrac{GM}{4 \pi^{2}} T^{2}\right)^{1/3} \\ & = \left(\dfrac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.00 \times 10^{30}\; kg)}{4 \pi^{2}} (75.3\; yr \times 365\; days/yr \times 24\; hr/day \times 3600\; s/hr)^{2}\right)^{1/3} \ldotp \end{split}\]

Hii inazalisha thamani ya 2.67 x 10 ¹² m au 17.8 AU kwa mhimili wa nusu-kuu. Mhimili wa nusu kuu ni nusu ya jumla ya aphelion na perihelion, hivyo tuna

\[\begin{split} a & = \frac{1}{2} (aphelion + perihelion) \\ aphelion & = 2a - perihelion \ldotp \end{split}\]

Kubadilisha maadili, tumegundua kwa mhimili wa nusu kuu na thamani iliyotolewa kwa perihelion, tunapata thamani ya aphelion kuwa 35.0 AU.

Umuhimu

Edmond Halley, kisasa cha Newton, kwanza alishukiwa kuwa comets tatu, zilizoripotiwa mwaka 1531, 1607, na 1682, zilikuwa kweli kimondo sawa. Kabla Tycho Brahe alifanya vipimo vya comets, iliaminika kuwa walikuwa matukio ya wakati mmoja, labda machafuko katika anga, na kwamba hawakuathiriwa na jua. Halley alitumia mechanics mpya ya Newton kutabiri kurudi kwake kwa kimondo kimondo mwaka 1758.

Mazoezi\(\PageIndex{1}\)

Obiti karibu ya mviringo ya Saturn ina radius wastani wa takriban 9.5 AU na ina kipindi cha miaka 30, ilhali Uranus wastani wa takriban 19 AU na ina kipindi cha miaka 84. Je, hii ni sambamba na matokeo yetu kwa comet Halley?