13.4: Nishati ya uwezo wa mvuto na Nishati ya Jumla

Malengo ya kujifunza

• Kuamua mabadiliko katika nishati ya uwezo wa mvuto juu ya umbali mkubwa
• Kuomba uhifadhi wa nishati kuamua kasi ya kutoroka
• Kuamua kama miili astronomical ni mvuto amefungwa

Tulijifunza nguvu za uwezo wa mvuto katika Nishati ya Uwezo na Uhifadhi wa Nishati, ambapo thamani ya\(g\) kubaki mara kwa mara. Sasa tunaendeleza maneno ambayo yanafanya kazi juu ya umbali kama vile g sio mara kwa mara. Hii ni muhimu kwa usahihi kuhesabu nishati zinazohitajika kuweka satelaiti katika obiti au kuwatuma kwenye misioni katika nafasi.

Gravitational uwezo Nishati zaidi ya Dunia

Tulifafanua kazi na nishati ya uwezo, hapo awali. Ufanisi wa ufafanuzi huo ni urahisi ambao tunaweza kutatua matatizo mengi kwa kutumia uhifadhi wa nishati. Nishati ya uwezo ni muhimu hasa kwa nguvu zinazobadilika na msimamo, kama nguvu ya mvuto inafanya juu ya umbali mkubwa. Katika Nishati ya Uwezo na Uhifadhi wa Nishati, tulionyesha kuwa mabadiliko katika nishati ya uwezo wa mvuto karibu na uso wa Dunia ni

\[ \Delta U = mg(y_2− y_1) \label{simple}\]

Hii inafanya kazi vizuri sana ikiwa\(g\) haibadilika kwa kiasi kikubwa kati ya y ₁ na y ₂. Tunarudi kwenye ufafanuzi wa kazi na nishati inayoweza kupata maneno ambayo ni sahihi juu ya umbali mkubwa. Kumbuka kwamba kazi (W) ni muhimu ya bidhaa dot kati ya nguvu na umbali. Kimsingi, ni bidhaa ya sehemu ya nguvu pamoja nyakati makazi yao kwamba makazi yao. Tunafafanua\(\Delta u\) kama hasi ya kazi iliyofanywa na nguvu tunayoshirikisha na nishati inayoweza. Kwa usahihi, tunapata maneno ya kusonga molekuli m kutoka umbali r ₁ kutoka katikati ya Dunia hadi umbali r ₂. Hata hivyo, matokeo yanaweza kuzalishwa kwa vitu viwili vinavyobadilisha kujitenga kwao kutoka thamani moja hadi nyingine.

Kielelezo\(\PageIndex{1}\): Kazi muhimu, ambayo huamua mabadiliko katika nishati ya uwezo, inaweza kupimwa kando ya njia iliyoonyeshwa nyekundu.

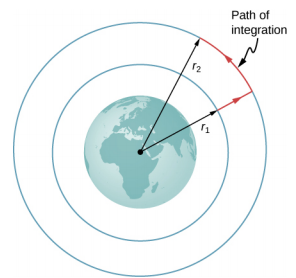
Fikiria Kielelezo\(\PageIndex{1}\), ambacho tunachukua m kutoka umbali r ₁ kutoka katikati ya Dunia hadi umbali ambao ni r ₂ kutoka katikati. Mvuto ni nguvu ya kihafidhina (ukubwa wake na mwelekeo ni kazi za eneo tu), hivyo tunaweza kuchukua njia yoyote tunayotaka, na matokeo ya hesabu ya kazi ni sawa. Tunachukua njia iliyoonyeshwa, kwa kuwa inaeleza sana ushirikiano. Sisi kwanza kuhamia radially nje kutoka umbali r ₁ kwa umbali r ₂, na kisha hoja pamoja na arc ya mduara mpaka sisi kufikia nafasi ya mwisho. Wakati wa sehemu radial,\(\vec{F}\) ni kinyume na mwelekeo sisi kusafiri pamoja d\(\vec{r}\), hivyo

\[E = K_1 + U_1 = K_2 + U_2\]

Pamoja na arc,\(\vec{F}\) ni perpendicular kwa d\(\vec{r}\), hivyo\(\vec{F}\; \cdotp d \vec{r}\) = 0. Hakuna kazi iliyofanywa tunapohamia pamoja na arc. Kutumia maneno kwa nguvu ya mvuto na kutambua maadili kwa\(\vec{F}\; \cdotp d \vec{r}\) pamoja makundi mawili ya njia yetu, tuna

\[ \begin{align} \Delta U &= - \int_{r_{1}}^{r_{2}} \vec{F}\; \cdotp d \vec{r} \\[4pt] &= GM_{E} m \int_{r_{1}}^{r_{2}} \frac{dr}{r^{2}} \\[4pt] &= GM_{E} m \left(\dfrac{1}{r_{1}} - \dfrac{1}{r_{2}}\right) \ldotp \label{eq13.3} \end{align} \]

Tangu\(\Delta U = U_2 − U_1\) tunaweza kupitisha kujieleza rahisi kwa\(U\):

\[U = - \frac{GM_{E} m}{r} \ldotp \label{13.4}\]

Kumbuka vitu viwili muhimu na ufafanuzi huu. Kwanza,\(U → 0\) kama\(r → \infty\). Nishati ya uwezo ni sifuri wakati raia wawili ni mbali sana. Tu tofauti katika\(U\) ni muhimu, hivyo uchaguzi wa\(U = 0\) kwa\(r = \infty\) ni moja tu ya urahisi. (Kumbuka kwamba katika matatizo ya mvuto mapema, ulikuwa huru kuchukua\(U = 0\) juu au chini ya jengo, au mahali popote.) Pili, kumbuka\(U\) kuwa inazidi kuwa mbaya zaidi kama raia kupata karibu. Hiyo ni sawa na yale uliyojifunza kuhusu nishati ya uwezo katika Nishati ya Uwezo na Uhifadhi wa Nishati. Kama raia wawili wanajitenga, kazi nzuri lazima ifanyike dhidi ya nguvu ya mvuto, na hivyo,\(U\) huongezeka (inakuwa chini ya hasi). Raia wote huanguka pamoja chini ya ushawishi wa mvuto, kuanguka kutoka juu hadi nishati ya chini.

Mfano\(\PageIndex{1}\): Lifting a Payload

Ni kiasi gani cha nishati kinachohitajika kuinua gari la Soyuz 9000-kg kutoka kwenye uso wa Dunia hadi urefu wa ISS, kilomita 400 juu ya uso?

Mkakati

Tumia Equation\ ref {eq13.3} ili kupata mabadiliko katika nishati ya uwezo wa malipo. Kiasi hicho cha kazi au nishati kinapaswa kutolewa ili kuinua malipo.

Suluhisho

Kuzingatia ukweli kwamba tunaanza kwenye uso wa Dunia na kuishia saa kilomita 400 juu ya uso, mabadiliko katika\(U\) ni

\[ \begin {align*} \Delta U &= U_{orbit} - U_{Earth} \\[4pt] &= - \dfrac{GM_{E} m}{R_{E} + 400\; km} - \left(- \dfrac{GM_{E} m}{R_{E}}\right) \ldotp \end{align*}\]

Sisi kuingiza maadili

• \(m = 9000\; kg\)
• \(M_{E} = 5.96 \times 10^{24}\; kg\)
• \(R_{E} = 6.37 \times 10^{6}\; m\)

na kubadilisha 400 km katika 4.00 x 10 ⁵ m. tunapata\(\Delta U = 3.32 \times 10^{10} J\). Ni chanya, kuonyesha ongezeko la nishati ya uwezo, kama tunavyotarajia.

Umuhimu

Kwa mtazamo, fikiria kwamba wastani wa matumizi ya nishati ya kaya ya Marekani mwaka 2013 ilikuwa 909 kWh kwa mwezi. Hiyo ni nishati ya

\[909\; kWh \times 1000\; W/kW \times 3600\; s/h = 3.27 \times 10^{9}\; J\; per\; month \ldotp \nonumber\]

Hivyo matokeo yetu ni matumizi ya nishati sawa na miezi 10. Hata hivyo, hii ni nishati tu zinazohitajika ili kuongeza kilomita 400 payload. Ikiwa tunataka Soyuz kuwa katika obiti ili iweze kukutana na ISS na sio tu kuanguka nyuma duniani, inahitaji nishati nyingi za kinetic. Kama tunavyoona katika sehemu inayofuata, nishati hiyo ya kinetic ni mara tano\(\Delta\) ile ya U. Aidha, nishati zaidi hutumiwa kuinua mfumo wa propulsion yenyewe. Nafasi ya kusafiri sio nafuu.

Zoezi\(\PageIndex{1}\)

Kwa nini usitumie kujieleza rahisi katika Equation\ ref {rahisi} badala? Hitilafu ingekuwa muhimu kiasi gani? (Thamani\(g\) ya kilomita 400 juu ya Dunia ni 8.67 m/s ².)

Uhifadhi wa Nishati

Katika Nishati ya Uwezo na Uhifadhi wa Nishati, tulielezea jinsi ya kutumia uhifadhi wa nishati kwa mifumo yenye nguvu za kihafidhina. Tuliweza kutatua matatizo mengi, hasa yale yanayohusisha mvuto, zaidi tu kutumia uhifadhi wa nishati. Kanuni hizo na mikakati ya kutatua matatizo hutumika sawa hapa. Mabadiliko tu ni kuweka kujieleza mpya kwa ajili ya nishati uwezo katika uhifadhi wa nishati equation,

\[E_{tot} = K_1 + U_1 = K_2 + U_2.\]

\[\frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \label{13.5}\]

Kumbuka kwamba tunatumia M, badala ya M _E, kama ukumbusho kwamba hatuzuiliwi na matatizo yanayohusisha Dunia. Hata hivyo, bado tunadhani kwamba m <<<M. (Kwa matatizo ambayo hii si kweli, tunahitaji kuingiza nishati ya kinetic ya raia wote na kutumia uhifadhi wa kasi ili kuhusisha kasi kwa kila mmoja. Lakini kanuni inabakia sawa.)

kutoroka kasi

Kasi ya kutoroka mara nyingi hufafanuliwa kuwa kasi ya chini ya awali ya kitu ambacho kinahitajika kutoroka uso wa sayari (au mwili wowote mkubwa kama mwezi) na kamwe kurudi. Kama kawaida, tunadhani hakuna nishati iliyopotea kwa anga, lazima iwe na yoyote.

Fikiria kesi ambapo kitu kinachozinduliwa kutoka kwenye uso wa sayari na kasi ya awali iliyoongozwa mbali na sayari. Kwa kasi ya chini inahitajika kutoroka, kitu kingekuja kupumzika kwa mbali sana, yaani, kitu kinatoa mwisho wa nishati yake ya kinetic kama inafikia infinity, ambapo nguvu ya mvuto inakuwa sifuri. Tangu U → 0 kama r →\(\infty\), hii inamaanisha nishati ya jumla ni sifuri. Kwa hiyo, tunapata kasi ya kutoroka kutoka kwenye uso wa mwili wa angani wa M na radius R kwa kuweka nishati ya jumla sawa na sifuri. Juu ya uso wa mwili, kitu iko\(r_1 = R\) na kina kasi ya kutoroka\(v_1 = v_{esc}\). Inafikia\(r_2 = \infty\) kwa kasi\(v_2 = 0\). Kubadilisha katika Equation\ ref {13.5}, tuna

\[\frac{1}{2} mv_{esc}^{2} - \frac{GMm}{R} = \frac{1}{2} m0^{2} - \frac{GMm}{\infty} = 0 \ldotp\]

Kutatua kwa kasi ya kutoroka,

\[v_{esc} = \sqrt{\frac{2GM}{R}} \ldotp \label{13.6}\]

Taarifa kwamba\(m\) ina kufutwa nje ya equation. Kasi ya kutoroka ni sawa kwa vitu vyote, bila kujali wingi. Pia, hatuzuiliwi kwenye uso wa sayari; R inaweza kuwa hatua yoyote ya kuanzia zaidi ya uso wa sayari.

Mfano\(\PageIndex{2}\): Escape from Earth

Je! Kasi ya kutoroka kutoka kwenye uso wa Dunia ni nini? Fikiria hakuna kupoteza nishati kutoka upinzani wa hewa. Linganisha hii na kasi ya kutoroka kutoka Jua, kuanzia obiti ya Dunia.

Mkakati

Tunatumia Equation 13.6, kufafanua wazi maadili ya R na M. kutoroka Dunia, tunahitaji wingi na radius ya Dunia. Kwa kukimbia Jua, tunahitaji wingi wa Jua, na umbali wa orbital kati ya Dunia na Jua.

Suluhisho

Kubadilisha maadili kwa wingi wa dunia na radius moja kwa moja kwenye Equation 13.6, tunapata

\[ \begin {align*} v_{esc} &= \sqrt{\frac{2GM}{R}} \\[4pt] &= \sqrt{\frac{2 (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{6.37 \times 10^{6}\; m}} \\[4pt] &= 1.12 \times 10^{4}\; m/s \ldotp \end{align*}\]

Hiyo ni kuhusu 11 km/s au 25,000 mph. Ili kuepuka Jua, kuanzia obiti ya Dunia, tunatumia R = R _ES = 1.50 x 10 ¹¹ m na M _Sun = 1.99 x 10 kilo ³⁰. Matokeo yake ni v _esc = 4.21 x 10 ⁴ m/s au kuhusu 42 km/s.

Umuhimu

Kasi inayohitajika kutoroka Jua (kuondoka mfumo wa jua) ni karibu mara nne kasi ya kutoroka kutoka kwenye uso wa dunia. Lakini kuna msaada katika kesi zote mbili. Dunia inazunguka, kwa kasi ya karibu 1.7 km/s kwenye ikweta, na tunaweza kutumia kasi hiyo kusaidia kutoroka, au kufikia obiti. Kwa sababu hii, makampuni mengi ya nafasi ya kibiashara yanadumisha vifaa vya uzinduzi karibu na ikweta. Ili kuepuka Jua, kuna msaada zaidi. Dunia inahusu Jua kwa kasi ya takriban 30 km/s Kwa uzinduzi katika mwelekeo kwamba Dunia ni kusonga, tunahitaji tu ziada 12 km/s. matumizi ya mvuto kusaidia kutoka sayari nyingine, kimsingi mbinu mvuto kombeo, inaruhusu probes nafasi kufikia kasi zaidi. Katika mbinu hii ya kombeo, gari inakaribia sayari na inaharakishwa na mvuto wa mvuto wa sayari. Ina kasi yake kubwa zaidi katika hatua ya karibu zaidi ya mbinu, ingawa inapungua kwa kipimo sawa kama inavyoondoka. Lakini kuhusiana na sayari, kasi ya gari mbali kabla ya mbinu, na kwa muda mrefu, ni sawa. Kama maelekezo ni kuchaguliwa kwa usahihi, ambayo inaweza kusababisha ongezeko kubwa (au kupungua kama inahitajika) katika kasi ya gari jamaa na wengine wa mfumo wa jua.

Nishati na vitu vyenye mvuto

Kama ilivyoelezwa hapo awali, kasi ya kutoroka inaweza kuelezwa kama kasi ya awali ya kitu ambacho kinaweza kutoroka uso wa mwezi au sayari. Kwa ujumla, ni kasi katika nafasi yoyote kama nishati ya jumla ni sifuri. Ikiwa nishati ya jumla ni sifuri au zaidi, kitu kinakimbia. Ikiwa jumla ya nishati ni hasi, kitu hakiwezi kutoroka. Hebu tuone kwa nini ndio kesi.

Kama ilivyoelezwa hapo awali, tunaona kwamba\(U → 0\) kama\(r → \infty\). Kama jumla ya nishati ni sifuri, basi kama m fika thamani ya r kwamba inakaribia infinity, U inakuwa sifuri na hivyo lazima nishati kinetic. Kwa hiyo, m huja kupumzika mbali sana na M. ina “tu alitoroka” M. kama nishati ya jumla ni chanya, basi nishati ya kinetic inabakia\(r = \infty\) na hakika m haina kurudi. Wakati nishati ya jumla ni sifuri au zaidi, basi tunasema kuwa m haifai kwa M.

Kwa upande mwingine, ikiwa nishati ya jumla ni hasi, basi nishati ya kinetic inapaswa kufikia sifuri kwa thamani fulani ya mwisho ya r, ambapo U ni hasi na sawa na nishati ya jumla. Kitu hawezi kamwe kuzidi umbali huu wa mwisho kutoka M, kwa kuwa kufanya hivyo itahitaji nishati ya kinetic kuwa hasi, ambayo haiwezekani. Tunasema m ni mvuto amefungwa kwa M.

Tumerahisisha mjadala huu kwa kudhani kwamba kitu kiliongozwa moja kwa moja mbali na sayari. Nini ni ajabu ni kwamba matokeo inatumika kwa kasi yoyote. Nishati ni kiasi cha scalar na hivyo Equation\ ref {13.5} ni equation scalar-mwelekeo wa kasi haina jukumu katika uhifadhi wa nishati. Inawezekana kuwa na mfumo wa kufungwa kwa mvuto ambapo raia hawawezi “kuanguka pamoja,” lakini kudumisha mwendo wa orbital kuhusu kila mmoja.

Tuna moja muhimu uchunguzi wa mwisho. Mapema tulisema kwamba ikiwa nishati ya jumla ni sifuri au zaidi, kitu kinakimbia. Kwa kusema, Equation\ ref {13.5} na Equation\ ref {13.6} kuomba vitu uhakika. Zinatumika kwa ukubwa wa mwisho, vitu vya ulinganifu wa spherically vilevile, ikiwa ni pamoja na kwamba thamani ya\(r\) katika Equation\ ref {13.5} daima ni kubwa kuliko jumla ya radii ya vitu viwili. Ikiwa r inakuwa chini ya jumla hii, basi vitu vinagongana. (Hata kwa maadili makubwa ya r, lakini karibu na jumla ya radii, nguvu mvuto mawimbi inaweza kusababisha athari kubwa kama vitu vyote ni ukubwa wa sayari. Sisi kuchunguza madhara ya mawimbi katika Vikosi vya Tidal.) Hakuna nishati nzuri wala hasi huzuia raia wa ukubwa wa mwisho kutoka kwenye mgongano. Kwa vitu halisi, mwelekeo ni muhimu.

Mfano\(\PageIndex{3}\): How Far Can an Object Escape?

Hebu tuchunguze mfano uliotangulia tena, ambapo tulihesabu kasi ya kutoroka kutoka Dunia na Jua, kuanzia obiti ya Dunia. Tulibainisha kuwa Dunia tayari ina kasi ya orbital ya 30 km/s Kama tunavyoona katika sehemu inayofuata, hiyo ni kasi ya tangential inahitajika kukaa katika obiti ya mviringo. Ikiwa kitu kilikuwa na kasi hii katika umbali wa obiti ya Dunia, lakini kilikuwa kikiongozwa moja kwa moja mbali na Jua, ingekuwa umbali gani utasafiri kabla ya kupumzika? Puuza madhara ya mvuto wa miili mingine yoyote.

Mkakati

Kitu kina nguvu za awali za kinetic na uwezo ambazo tunaweza kuhesabu. Wakati kasi yake inafikia sifuri, iko umbali wake wa juu kutoka Jua. Tunatumia Equation 13.5, uhifadhi wa nishati, ili kupata umbali ambao nishati ya kinetic ni sifuri.

Suluhisho

Msimamo wa awali wa kitu ni radius ya dunia ya obiti na kasi ya awali inapewa kama 30 km/s. kasi ya mwisho ni sifuri, hivyo tunaweza kutatua kwa umbali katika hatua hiyo kutoka uhifadhi wa nishati equation. Kutumia R _ES = 1.50 x 10 ¹¹ m na M _Sun = 1.99 x 10 kilo ³⁰, tuna

\[\begin{split} \frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} & = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \\ \frac{1}{2} \cancel{m} (30\; km/s)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{1.50 \times 10^{11}\; m} & = \frac{1}{2} m(0)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{r_{2}} \end{split}\]

ambapo molekuli m cancels. Kutatua kwa r ₂ tunapata r ₂ = 3.0 x 10 ¹¹ m Kumbuka kuwa hii ni umbali wa kwanza kutoka Jua na inatuchukua nyuma ya obiti ya Mars, lakini sio kabisa kwa ukanda wa asteroid.

Umuhimu

Kitu katika kesi hii kilifikia umbali hasa mara mbili umbali wa awali wa orbital. Tutaona sababu ya hii katika sehemu inayofuata tunapohesabu kasi ya mzunguko wa mviringo.

Zoezi\(\PageIndex{3}\)

Kudhani wewe ni katika spacecraft katika obiti kuhusu Sun katika obiti ya dunia, lakini mbali na Dunia (ili iweze kupuuzwa). Unawezaje kuelekeza kasi yako tangential kwa mwelekeo radial kama kwamba unaweza kisha kupita kwa obiti Mars? Ni nini kinachohitajika kubadili tu mwelekeo wa kasi?