13.3: Gravitation Karibu na uso wa Dunia

Malengo ya kujifunza

• Eleza uhusiano kati ya G na g ya mara kwa mara
• Kuamua wingi wa mwili wa astronomical kutoka kwa kasi ya kuanguka kwa bure kwenye uso wake
• Eleza jinsi thamani ya g inatofautiana kutokana na eneo na mzunguko wa Dunia

Katika sehemu hii, tunaona jinsi sheria ya Newton ya uvunjaji inatumika kwenye uso wa sayari na jinsi inavyounganisha na kile tulichojifunza mapema kuhusu kuanguka kwa bure. Pia tunachunguza madhara ya mvuto ndani ya miili ya spherical.

Uzito

Kumbuka kwamba kasi ya kitu cha kuanguka bure karibu na uso wa Dunia ni takriban g = 9.80 m/s ². Nguvu inayosababisha kasi hii inaitwa uzito wa kitu, na kutoka kwa sheria ya pili ya Newton, ina thamani mg. Uzito huu umepo bila kujali kama kitu kiko katika kuanguka kwa bure. Sasa tunajua kwamba nguvu hii ni nguvu ya mvuto kati ya kitu na Dunia. Ikiwa tunabadilisha mg kwa ukubwa wa\(\vec{F}_{12}\) sheria ya Newton ya uharibifu wa ulimwengu wote, m kwa m ₁, na M _E kwa m ₂, tunapata equation ya scalar

\[mg = G \frac{m M_{E}}{r^{2}} \label{13.1}\]

ambapo r ni umbali kati ya vituo vya wingi wa kitu na Dunia. Radi ya wastani ya Dunia ni takriban kilomita 6370. Kwa hiyo, kwa vitu ndani ya kilomita chache za uso wa Dunia, tunaweza kuchukua\(r = R_E\) (Kielelezo\(\PageIndex{1}\)). Masi m ya kitu hufuta, na kuacha

\[g = G \frac{M_{E}}{r^{2}} \ldotp \label{13.2}\]

Hii inaelezea kwa nini raia wote huanguka kwa kasi sawa. Tumepuuza ukweli kwamba Dunia pia inaharakisha kuelekea kitu kilichoanguka, lakini hiyo inakubalika kwa muda mrefu kama masi ya Dunia ni kubwa zaidi kuliko ile ya kitu.

Kielelezo\(\PageIndex{1}\): Tunaweza kuchukua umbali kati ya vituo vya wingi wa Dunia na kitu juu ya uso wake kuwa radius ya Dunia, isipokuwa ukubwa wake ni kidogo sana kuliko radius ya Dunia.

Mfano\(\PageIndex{1}\): Masses of Earth and Moon

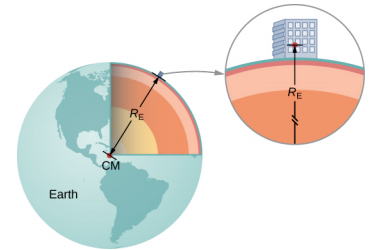
Je! Umewahi kujiuliza jinsi tunavyojua wingi wa Dunia? Hakika hatuwezi kuiweka kwa kiwango. Maadili ya g na radius ya Dunia yalipimwa kwa usahihi wa kuridhisha karne zilizopita.

1. Tumia maadili ya kawaida ya g, R _E, na Equation\ ref {13.2} ili upate masi ya Dunia.
2. Tathmini thamani ya g kwenye Mwezi. Tumia ukweli kwamba Mwezi una radius ya kilomita 1700 (thamani ya usahihi huu iliamua karne nyingi zilizopita) na kudhani ina wiani sawa wa wastani kama Dunia, 5500 kg/m ³.

Mkakati

Kwa maadili inayojulikana ya g na R _E, tunaweza kutumia Equation\ ref {13.2} ili kupata M _E. Kwa Mwezi, tunatumia dhana ya wiani sawa wa wastani ili kuamua wingi kutoka kwa uwiano wa kiasi cha Dunia na Mwezi.

Suluhisho

1. Kupanga upya Equation\ ref {13.2}, tuna $$ M_ {E} =\ frac {g R_ {E} ^ {2}} {G} =\ frac {(9.80\; m/s^ {2}) (6.37\ mara 10^ {6}\;\ cdotp m^ {2} /kg^ {2}} = 5.95\ mara 10^ {24}\; kilo\ ldotp$$
2. Kiasi cha tufe ni sawia na radius cubed, hivyo uwiano rahisi unatupa $$\ frac {M_ {M}} {M_ {E}} =\ frac {R_ {M} ^ {3}} {R_ {E} ^ {3}}\ rightarrow M_ {M} =\ kushoto (\ dfrac {(1.7\ mara 10^ {6}\ m) ^ {3}} {(6.37\ mara 10^ {6}\; m) ^ {3}}\ haki) (5.95\ mara 10^ {24}\; kg) = 1.1\ mara 10^ {23}\; kilo\ LDOTP $Tunatumia sasa Ulinganisho\ ref {13.2}. $g_ {M} = G\ frac {M_ {M} {r_ {M} ^ {2}} = (6.67\ mara 10^ {-11}\; N\;\ cdotp m^ {2} /kg^ {2})\ kushoto (\ dfrac {1.1\ mara 10^ {23}\; kg} {(1.7\ mara 10^ {6}\; m) ^ {2}}\ haki) = 2.5\; m/s^ {2} $$

Umuhimu

Mara tu Cavendish aliamua thamani ya G mwaka 1798, wingi wa Dunia unaweza kuhesabiwa. (Kwa kweli, hiyo ilikuwa lengo kuu la majaribio ya Cavendish katika nafasi ya kwanza.) Thamani tuliyohesabu kwa g ya Mwezi si sahihi. Uzito wa wastani wa Mwezi ni kweli 3340 kg/m ³ na g = 1.6 m/s ² juu ya uso. Newton alijaribu kupima masi ya Mwezi kwa kulinganisha athari za Jua kwenye mawimbi ya bahari ya Dunia ikilinganishwa na ile ya Mwezi. Thamani yake ilikuwa sababu ya mbili ndogo mno. Maadili sahihi zaidi kwa g na wingi wa Mwezi hutoka kwa kufuatilia mwendo wa spacecraft ambayo imezunguka Mwezi. Lakini wingi wa Mwezi unaweza kuamua kwa usahihi bila kwenda Mwezi. Dunia na mzunguko wa Mwezi kuhusu kituo cha kawaida cha wingi, na vipimo vya angani vya makini vinaweza kuamua eneo hilo. Uwiano wa masi ya Mwezi kwa Dunia ni uwiano wa [umbali kutoka kituo cha kawaida cha masi hadi kituo cha Mwezi] hadi [umbali kutoka kituo cha kawaida cha masi hadi kituo cha dunia].

Baadaye katika sehemu hii, tutaona kwamba wingi wa miili mingine ya astronomical pia inaweza kuamua na kipindi cha satelaiti ndogo zinazozunguka. Lakini mpaka Cavendish kuamua thamani ya G, raia wa miili hii yote haijulikani.

Mfano\(\PageIndex{2}\): Gravity above Earth’s Surface

ni thamani ya g 400 km juu ya uso wa dunia, ambapo International Space Station ni katika obiti?

Suluhisho

Kutumia thamani ya M _E na kutambua radius ni r = R _E + 400 km, tunatumia Equation\ ref {13.2} ili kupata g. kutoka Equation\ ref {13.2} tuna

\[g = G \frac{M_{E}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \left(\dfrac{5.96 \times 10^{24}\; kg}{(6.37 \times 10^{6} + 400 \times 10^{3}\; m)^{2}}\right) = 8.67\; m/s^{2} \ldotp\]

Umuhimu

Mara nyingi tunaona video ya wanaanga katika vituo vya nafasi, inaonekana kuwa na uzito. Lakini wazi, nguvu ya mvuto inawafanya. Kulinganisha thamani ya g sisi tu mahesabu ya kwamba duniani (9.80 m/s ²), tunaona kwamba astronauts katika International Space Station bado 88% ya uzito wao. Wao huonekana tu kuwa na uzito kwa sababu wao ni katika kuanguka bure. Sisi kurudi hii katika Orbits Satellite na Nishati.

Zoezi\(\PageIndex{1}\)

Uzito wako juu ya jengo refu unalinganishaje na hilo kwenye ghorofa ya kwanza? Je! Unafikiri wahandisi wanahitaji kuzingatia mabadiliko katika thamani ya g wakati wa kubuni msaada wa miundo kwa jengo kubwa sana?

Uwanja wa mvuto

Equation\ ref {13.2} ni equation ya scalar, ikitoa ukubwa wa kuongeza kasi ya mvuto kama kazi ya umbali kutoka katikati ya masi inayosababisha kuongeza kasi. Lakini tungeweza kubakia fomu ya vector kwa nguvu ya mvuto katika Equation\ ref {13.1}, na kuandika kuongeza kasi katika fomu ya vector kama

\[\vec{g} = G \frac{M}{r^{2}} \hat{r} \ldotp\]

Sisi kutambua uwanja vector kuwakilishwa na\(\vec{g}\) kama uwanja mvuto unasababishwa na molekuli M. tunaweza picha shamba kama inavyoonekana Kielelezo\(\PageIndex{2}\). Mstari huelekezwa radially ndani na ni kusambazwa kwa usawa juu ya wingi.

Kielelezo\(\PageIndex{2}\): Uwakilishi wa tatu-dimensional wa uwanja wa mvuto ulioundwa na molekuli M Kumbuka kwamba mistari ni kusambazwa kwa usawa katika pande zote. (Sanduku limeongezwa tu kwa misaada katika taswira.)

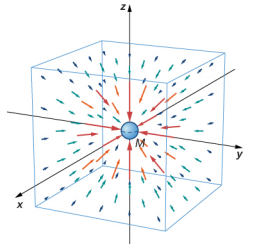
Kama ilivyo kweli kwa shamba lolote la vector, mwelekeo wa\(\vec{g}\) ni sawa na mistari ya shamba wakati wowote. Nguvu ya\(\vec{g}\) wakati wowote ni inversely sawia na nafasi ya mstari. Njia nyingine ya kusema hii ni kwamba ukubwa wa shamba katika eneo lolote ni sawa na idadi ya mistari ambayo hupita eneo la uso wa kitengo, kwa ufanisi wiani wa mistari. Kwa kuwa mistari ni sawa na nafasi katika pande zote, idadi ya mistari kwa eneo la uso wa kitengo umbali r kutoka kwa wingi ni idadi ya mistari iliyogawanywa na eneo la uso wa eneo la radius r, ambayo ni sawa na r 2. Kwa hiyo, picha hii inawakilisha kikamilifu sheria ya mraba inverse, pamoja na kuonyesha mwelekeo wa shamba. Katika picha ya shamba, tunasema kuwa molekuli m inakabiliana na uwanja wa mvuto wa molekuli M. tutatumia dhana ya mashamba kwa faida kubwa katika sehemu za baadaye juu ya electromagnetism.

Uzito wa dhahiri: Uhasibu wa Mzunguko wa Dunia

Kama tulivyoona katika Maombi ya Sheria Newton, vitu kusonga kwa kasi ya mara kwa mara katika mduara na kuongeza kasi centripetal kuelekezwa kuelekea katikati ya mduara, ambayo ina maana kwamba kuna lazima kuwe na nguvu wavu kuelekezwa kuelekea katikati ya mduara huo. Kwa kuwa vitu vyote vilivyo juu ya uso wa Dunia vinapitia mduara kila baada ya masaa 24, kuna lazima iwe na nguvu ya centripetal ya wavu kwenye kila kitu kilichoelekezwa kuelekea katikati ya mduara huo.

Hebu tuangalie kwanza kitu cha molekuli m iko kwenye equator, imesimamishwa kwa kiwango (Kielelezo\(\PageIndex{3}\)). Kiwango kina nguvu ya juu\(\vec{F}_{s}\) mbali na kituo cha dunia. Hii ni kusoma kwa kiwango, na hivyo ni uzito wa dhahiri wa kitu. Uzito (mg) unaelekea katikati ya Dunia. Ikiwa Dunia haikugeuka, kasi itakuwa sifuri na, kwa hiyo, nguvu ya wavu itakuwa sifuri, na kusababisha F _s = mg. Hii itakuwa kusoma kweli ya uzito.

Kielelezo\(\PageIndex{3}\): Kwa mtu amesimama kwenye equator, kasi ya centripetal (ac) iko katika mwelekeo sawa na nguvu ya mvuto. Katika latitude\(\lambda\), angle kati ya ac na nguvu ya mvuto ni\(\lambda\) na ukubwa wa ac hupungua na\(\cos \lambda\).

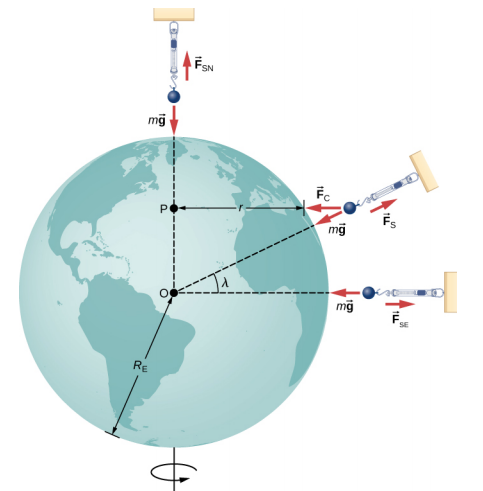
Kwa mzunguko, jumla ya majeshi haya yanapaswa kutoa kasi ya centripetal,\(a_c\). Kwa kutumia sheria ya pili ya Newton, tuna

\[\sum F = F_{s} - mg = ma_{c} \quad where\; a_{c} = - \frac{v^{2}}{r} \ldotp \label{13.3}\]

Kumbuka kuwa _c inaelezea mwelekeo sawa na uzito; kwa hiyo, ni hasi. kasi tangential v ni kasi katika ikweta na r ni R _E. Tunaweza kuhesabu kasi tu kwa kutambua kwamba vitu kwenye ikweta vinasafiri mzunguko wa Dunia katika masaa 24. Badala yake, hebu kutumia kujieleza mbadala kwa _c kutoka Motion katika mbili na Tatu Vipimo. Kumbuka kwamba kasi ya tangential inahusiana na kasi ya angular (\(\omega\)) na v = r\(\omega\). Hivyo, tuna _c = -r\(\omega\) ². Kwa kupanga upya Equation 13.3 na kubadilisha r = R _E, uzito dhahiri katika ikweta ni

\[F_{s} = m (g - R_{E} \omega^{2}) \ldotp\]

Kasi ya angular ya Dunia kila mahali ni

\[\omega = \frac{2 \pi\; rad}{24\; hr \times 3600\; s/hr} = 7.27 \times 10^{-5}\; rad/s \ldotp\]

Kubadilisha maadili ya R _E na\(\omega\), tuna R _E\(\omega\) ² = 0.0337 m/s ². Hii ni 0.34% tu ya thamani ya mvuto, hivyo ni wazi marekebisho madogo.

Mfano\(\PageIndex{3}\): Zero Apparent Weight

Je, Dunia ingekuwa na kasi gani kwa ajili ya wale walio katika ikweta kuwa na uzito wa dhahiri wa sifuri? Urefu wa siku utakuwa muda gani?

Mkakati

Kutumia Equation\ ref {13.3}, tunaweza kuweka uzito dhahiri (F _s) kwa sifuri na kuamua kasi centripetal required. Kutoka hapo, tunaweza kupata kasi katika ikweta. Urefu wa siku ni wakati unaohitajika kwa mzunguko mmoja kamili.

Suluhisho

Kutoka Equation\ ref {13.2}, tuna\(\sum\) F = F _s - mg = ma _c, hivyo kuweka F _s = 0, tunapata g = _c. Kutumia maneno kwa _c, kubadilisha nafasi ya radius ya Dunia na thamani ya kawaida ya mvuto, tunapata

\[\begin{split} a_{c} & = \frac{v^{2}}{r} = g \\ v & = \sqrt{gr} = \sqrt{(9.80\; m/s^{2})(6.37 \times 10^{6}\; m)} = 7.91 \times 10^{3}\; m/s \ldotp \end{split}\]

Kipindi cha T ni wakati wa mzunguko mmoja kamili. Kwa hiyo, kasi ya tangential ni mzunguko umegawanyika na T, kwa hiyo tuna

\[\begin{split} v & = \frac{2 \pi r}{T} \\ T & = \frac{2 \pi r}{v} = \frac{2 \pi (6.37 \times 10^{6}\; m)}{7.91 \times 10^{3}\; m/s} = 5.06 \times 10^{3}\; s \ldotp \end{split}\]

Hii ni dakika 84.

Umuhimu

Tutaona baadaye katika sehemu hii kwamba kasi hii na urefu wa siku pia itakuwa kasi ya orbital na kipindi cha satellite katika obiti kwenye uso wa dunia. Ilhali obiti hiyo haikuwezekana karibu na uso wa Dunia kutokana na upinzani wa hewa, hakika inawezekana maili mia chache tu juu ya Dunia.

Matokeo Mbali na Ikweta

Katika miti, _c → 0 na Fs = mg, kama ilivyo bila mzunguko. Katika latitude nyingine yoyote\(\lambda\), hali ni ngumu zaidi. Kasi ya centripetal inaelekezwa kuelekea hatua P katika takwimu, na radius inakuwa\(r = R_E \cos \lambda\). Jumla ya vector ya uzito na\(\vec{F}_{s}\) lazima ielekeze kuelekea hatua P, kwa hiyo haifai\(\vec{F}_{s}\) tena katikati ya Dunia. (Tofauti ni ndogo na imeenea katika takwimu.) Bob bob daima inaelezea pamoja na mwelekeo huu uliopotea. Majengo yote yamejengwa iliyokaa pamoja na mwelekeo huu uliopotea, sio pamoja na radius kupitia katikati ya Dunia. Kwa majengo marefu zaidi, hii inawakilisha kupotoka kwa miguu michache juu.

Pia ni muhimu kutambua kwamba Dunia sio nyanja kamili. Mambo ya ndani ni sehemu ya kioevu, na hii inaboresha Dunia bulging katika equator kutokana na mzunguko wake. Radi ya Dunia ni takriban kilomita 30 zaidi kwenye ikweta ikilinganishwa na miti. Imeachwa kama zoezi la kulinganisha nguvu ya mvuto kwenye fito na ile kwenye ikweta kwa kutumia Equator\ ref {13.2}. Tofauti ni sawa na tofauti kutokana na mzunguko na iko katika mwelekeo huo. Inaonekana, unaweza kupoteza “uzito” kwa kuhamia kwenye kitropiki.

Gravity Mbali na uso

Mapema tulisema bila ushahidi kwamba sheria ya gravitation inatumika kwa vitu vyenye usawa, ambapo wingi wa kila mwili hufanya kama ilivyokuwa katikati ya mwili. Tangu Equation\ ref {13.2} imetokana na Equation\ ref {13.1}, pia ni halali kwa mgawanyo wa wingi wa ulinganifu, lakini milinganyo yote ni halali tu kwa maadili ya\(r ≥ R_E\). Kama tulivyoona katika Mfano 13.4, kwenye kilomita 400 juu ya uso wa Dunia, ambapo Kituo cha Kimataifa cha Space kinazunguka, thamani ya\(g\) ni 8.67 m/s ². (Tutaona baadaye kwamba hii pia ni kasi ya centripetal ya ISS.)

Kwa\(r < R_E\), Equation\ ref {13.1} na Equation\ ref {13.2} si halali. Hata hivyo, tunaweza kuamua g kwa kesi hizi kwa kutumia kanuni inayotokana na sheria ya Gauss, ambayo ni chombo chenye nguvu cha hisabati ambacho tunasoma kwa undani zaidi baadaye katika kozi. Matokeo ya sheria ya Gauss, kutumika kwa gravitation, ni kwamba tu wingi ndani r inachangia nguvu mvuto. Pia, umati huo, kama hapo awali, unaweza kuchukuliwa kuwa iko katikati. Athari ya mvuto wa wingi nje r ina athari zero wavu.

Matukio mawili ya kuvutia sana hutokea. Kwa sayari ya spherical na wiani wa mara kwa mara, wingi ndani ya r ni mara wiani kiasi ndani ya r. molekuli hii inaweza kuchukuliwa iko katikati. Kubadilisha M _E na wingi tu ndani ya r, M =\(\rho\) x (kiasi cha nyanja), na R _E na r, Equation\ ref {13.2} inakuwa

\[g = G \frac{M_{E}}{R_{E}^{2}} = G \frac{\rho \left(\dfrac{4}{3} \pi r^{3}\right)}{r^{2}} = \frac{4}{3} G \rho \pi r \ldotp\]

Thamani ya g, na hivyo uzito wako, hupungua kwa mstari unapotoka chini ya shimo katikati ya sayari ya spherical. Katikati, wewe ni uzito, kama wingi wa sayari huchota sawa katika pande zote. Kweli, wiani wa Dunia sio mara kwa mara, wala Dunia haina imara kote. Kielelezo\(\PageIndex{4}\) inaonyesha wasifu wa\(g\) kama Dunia alikuwa na wiani mara kwa mara na profile uwezekano zaidi kulingana na makadirio ya wiani inayotokana na data seismic.

Kielelezo\(\PageIndex{4}\): Kwa r <RE, thamani ya g kwa kesi ya wiani wa mara kwa mara ni mstari wa kijani wa moja kwa moja. Mstari wa bluu kutoka PREM (Mfano wa Kwanza wa Kumbukumbu ya Dunia) labda ni karibu na wasifu halisi wa g.

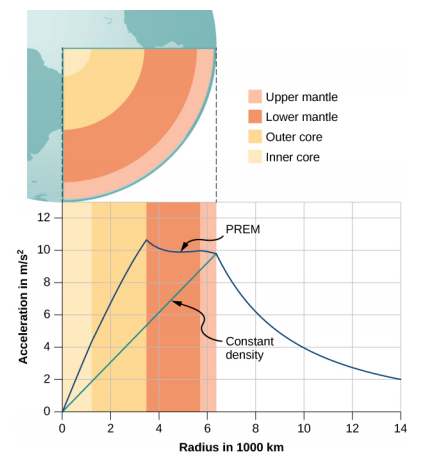
Kesi ya pili ya kuvutia inahusisha kuishi kwenye sayari ya shell ya spherical. Hali hii imependekezwa katika hadithi nyingi za sayansi za uongo. Kupuuza masuala muhimu ya uhandisi, shell inaweza kujengwa na radius taka na jumla ya wingi, kama kwamba g juu ya uso ni sawa na Dunia.Je, unaweza nadhani nini kinatokea mara moja kushuka katika lifti ndani ya shell, ambapo hakuna molekuli kati yako na katikati? Ni faida gani hii itatoa kwa kusafiri umbali mkubwa kutoka sehemu moja kwenye nyanja hadi nyingine? Na hatimaye, ingekuwa na athari gani ikiwa sayari ilikuwa inazunguka?