16.3: Ndege Mawimbi ya umeme

Last updated
Save as PDF

Page ID: 176583

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

MALENGO YA KUJIFUNZA

Mwishoni mwa sehemu hii, utaweza:

Eleza jinsi equations ya Maxwell inavyotabiri maelekezo ya jamaa ya mashamba ya umeme na mashamba magnetic, na mwelekeo wa uenezi wa mawimbi ya umeme ya ndege
Eleza jinsi equations ya Maxwell inavyotabiri kwamba kasi ya uenezi wa mawimbi ya umeme katika nafasi ya bure ni kasi ya mwanga
Tumia ukubwa wa jamaa wa mashamba ya umeme na magnetic katika wimbi la ndege ya umeme
Eleza jinsi mawimbi ya umeme yanavyozalishwa na kugunduliwa

Mawimbi ya mitambo yanasafiri kwa njia ya kati kama kamba, maji, au hewa. Pengine utabiri muhimu zaidi wa milinganyo ya Maxwell ni kuwepo kwa mashamba ya pamoja ya umeme na magnetic (au sumakuumeme) yanayoeneza kupitia angani kama mawimbi ya sumakuumeme. Kwa sababu equations ya Maxwell inashikilia nafasi ya bure, mawimbi ya umeme yaliyotabiriwa, tofauti na mawimbi ya mitambo, hauhitaji kati ya uenezi wao.

Matibabu ya jumla ya fizikia ya mawimbi ya umeme ni zaidi ya upeo wa kitabu hiki. Tunaweza, hata hivyo, kuchunguza kesi maalum ya wimbi la umeme linaloenea kupitia nafasi ya bure pamoja na x -axis ya mfumo wa kuratibu uliopewa.

Mawimbi ya umeme katika Mwelekeo mmoja

Wimbi la umeme lina shamba la umeme, linaloelezwa kama kawaida kwa suala la nguvu kwa malipo kwa malipo ya kituo, na shamba la magnetic, linaloelezwa kwa nguvu kwa malipo kwa malipo ya kusonga. Sehemu ya sumakuumeme inadhaniwa kuwa kazi ya x -kuratibu tu na wakati. Sehemu ya y ya shamba la umeme huandikwa kama\(E_y (x,t)\), sehemu ya z ya shamba la magnetic kama\(B_z (x,t)\), nk Kwa sababu tunachukua nafasi ya bure, hakuna malipo ya bure au mikondo, ili tuweze kuweka\(Q_{in} = 0\) na\(I = 0\) katika equations ya Maxwell.

Hali ya transverse ya mawimbi ya umeme

Tunachunguza kwanza sheria ya Gauss kwa mashamba ya umeme inamaanisha kuhusu maelekezo ya jamaa ya uwanja wa umeme na mwelekeo wa uenezi katika wimbi la umeme. Fikiria uso wa Gaussia kuwa uso wa sanduku la mstatili ambao sehemu ya msalaba ni mraba wa upande l na ambao upande wa tatu una urefu\(\Delta x\), kama inavyoonekana kwenye Mchoro\(\PageIndex{1}\). Kwa sababu uwanja umeme ni kazi tu ya x na t, y -sehemu ya shamba umeme ni sawa juu ya wote juu (kinachoitwa Side 2) na chini (kinachoitwa Side 1) ya sanduku, ili michango hizi mbili kwa flux kufuta. Hoja inayofanana pia inashikilia mtiririko wa wavu kutoka kwa z -sehemu ya shamba la umeme kupitia Pande 3 na 4. Flux yoyote ya wavu kupitia uso kwa hiyo inakuja kabisa kutoka kwa sehemu ya x ya shamba la umeme. Kwa sababu uwanja umeme hana y - au z -utegemezi,\(E_x(x,t)\) ni mara kwa mara juu ya uso wa sanduku na eneo A na ina thamani uwezekano tofauti\(E_x (x + \Delta x, t)\) ambayo ni mara kwa mara juu ya uso kinyume cha sanduku.

Kutumia sheria Gauss ya anatoa

\[\text{Net flux} = - E_x (x,t) A + E_x (x + \Delta x, t) A = \dfrac{Q_{in}}{\epsilon_0} \label{16.13}\]

\(A = l \times l\)wapi eneo la nyuso za mbele na nyuma za uso wa mstatili. Lakini malipo iliyoambatanishwa ni\(Q_{in} = 0\), hivyo flux ya sehemu hii ya wavu pia ni sifuri, na Equation\ ref {16.13} ina maana\(E_x (x,t) = E_x (x + \Delta x, t)\) kwa yoyote\(\Delta x\). Kwa hiyo, ikiwa kuna sehemu ya x ya shamba la umeme, haiwezi kutofautiana na x. shamba sare ya aina hiyo ingekuwa tu superposed artificially juu ya wimbi kusafiri, kwa mfano, kwa kuwa na jozi ya sahani sambamba kushtakiwa. Sehemu hiyo haiwezi\(E_x(x,t)\) kuwa sehemu ya wimbi la sumakuumeme linaloenea kando ya x -axis; hivyo\(E_x(x,t) = 0\) kwa wimbi hili. Kwa hiyo, vipengele pekee vya nonzero vya uwanja wa umeme ni\(E_y(x,t)\) na\(E_z(x,t)\) perpendicular kwa mwelekeo wa uenezi wa wimbi.

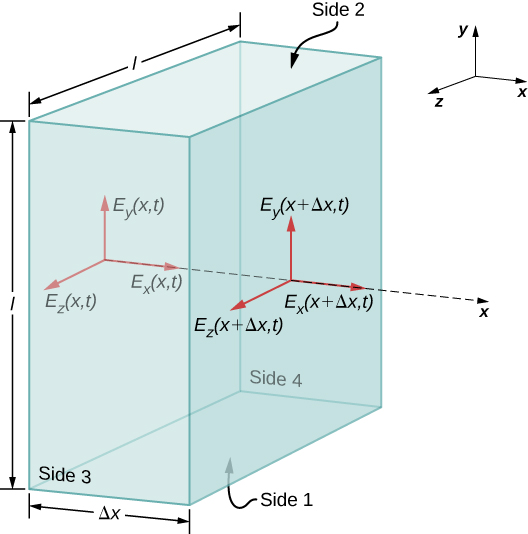
Kielelezo inaonyesha sanduku mstatili wa vipimo l na l na delta x. juu na chini pande, sambamba na ndege xz ni kinachoitwa upande 2 na upande 1 mtiririko. Pande za mbele na nyuma, sambamba na ndege ya xy zimeandikwa upande 3 na upande wa 4 kwa mtiririko huo. Mishale mitatu inatoka kwenye hatua upande wa kushoto. Hizi ni pamoja x, y na z mhimili na ni mtiririko kinachoitwa E subscript x mabano x, t mabano, E subscript y mabano x, t mabano na E subscript z mabano x, t mabano. Mishale mitatu zaidi inatoka mahali ambapo mhimili wa x unaingilia upande wa kulia wa sanduku. Hizi, pia, ni pamoja na mhimili x, y na z na ni mtiririko kinachoitwa E subscript x mabano x plus delta x, t mabano, E Subscript y mabano x plus delta x plus delta x, t mabano na E Subscript z mabano x plus delta x, t mabano. — Kielelezo\(\PageIndex{1}\): The surface of a rectangular box of dimensions \(l \times l \times \Delta x\) is our Gaussian surface. The electric field shown is from an electromagnetic wave propagating along the x-axis.

A similar argument holds by substituting E for B and using Gauss’s law for magnetism instead of Gauss’s law for electric fields. This shows that the B field is also perpendicular to the direction of propagation of the wave. The electromagnetic wave is therefore a transverse wave, with its oscillating electric and magnetic fields perpendicular to its direction of propagation.

The speed of propagation of electromagnetic waves

We can next apply Maxwell’s equations to the description given in connection with Figure 16.2.3 in the previous section to obtain an equation for the E field from the changing B field, and for the B field from a changing E field. We then combine the two equations to show how the changing E and B fields propagate through space at a speed precisely equal to the speed of light.

First, we apply Faraday’s law over Side 3 of the Gaussian surface, using the path shown in Figure \(\PageIndex{2}\). Because \(E_x(x,t) = 0\), we have

\[\oint \vec{E} \cdot d\vec{s} = - E_y(x,t)l + E_y(x + \Delta x,t)l.\]

Assuming \(\Delta x\) is small and approximating \(E_y (x + \Delta x,t)\) by

\[E_y (x + \Delta x,t) = E_y (x,t) + \dfrac{\partial E_y(x,t)}{\partial x} \Delta x,\]

we obtain

\[\oint \vec{E} \cdot d\vec{s} = \dfrac{\partial E_y (x,t)}{\partial x} (l\Delta x).\]

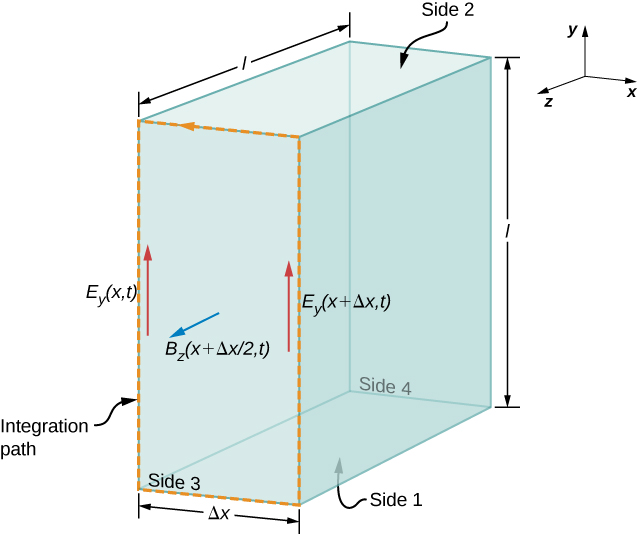
Figure shows a rectangular box of dimensions l by l by delta x. The top and bottom sides, parallel to the xz plane are labeled side 2 and side 1 respectively. The front and back sides, parallel to the xy plane are labeled side 3 and side 4 respectively. The boundary of side 3 is labeled integration path. Two arrows along side 3, pointing upwards in the positive y direction are labeled E subscript y parentheses x,t parentheses and E subscript y parentheses x plus delta x,t parentheses. An arrow on the left side of the box, pointing in the positive z direction is labeled B subscript z parentheses x plus delta x by 2,t parentheses. — Kielelezo\(\PageIndex{2}\): Tunatumia sheria ya Faraday mbele ya mstatili kwa kutathmini\(\oint \vec{E} \cdot d\vec{s}\) kando ya makali ya mstatili wa Side 3 katika mwelekeo ulioonyeshwa, kuchukua uwanja wa B kuvuka uso kuwa takriban thamani yake katikati ya eneo lililopita.

Kwa sababu\(\Delta x\) ni ndogo, mtiririko wa magnetic kupitia uso unaweza kuhesabiwa na thamani yake katikati ya eneo lililopita, yaani\(B_z\left(x + \dfrac{\Delta x}{2}, t\right)\). Flux ya uwanja B kupitia Face 3 ni kisha uwanja B mara eneo hilo,

\[\oint_S \vec{B} \cdot \vec{n} dA = B_z \left(x + \dfrac{\Delta x}{2}, t\right) (l \Delta x). \label{16.14}\]

Kutoka kwa sheria ya Faraday,

\[\oint \vec{E} \cdot d\vec{s} = -\dfrac{d}{dt} \int_S \vec{B} \cdot \vec{n} dA.\label{16.15}\]

Kwa hiyo, kutoka equations\ ref {16.13} na\ ref {16.14},

\[\dfrac{\partial E_y (x,t)}{\partial x} (l \Delta x) = - \dfrac{\partial}{\partial t} \left[ B_z \left( x + \dfrac{\Delta x}{2}, t\right) \right] (l\Delta x).\]

Kufuta\(l \Delta x\) na kuchukua kikomo kama\(\Delta x = 0\), sisi ni wa kushoto na

\[\dfrac{\partial E_y (x,t)}{\partial x} = - \dfrac{\partial B_z(x,t)}{\partial t}. \label{16.16}\]

Tunaweza kuwa kutumika sheria Faraday badala ya uso juu (kuhesabiwa 2) katika Kielelezo\(\PageIndex{2}\), ili kupata equation kusababisha

\[\dfrac{\partial B_z(x,t)}{\partial t} = - \dfrac{\partial E_y (x,t)}{\partial x}. \label{16.17}\]

Hii ni equation inayoelezea shamba la E linalotegemea spatially lililozalishwa na uwanja wa B unategemea wakati.

Halafu tunatumia sheria ya Ampère-Maxwell (na\(I = 0\)) juu ya nyuso mbili sawa (Surface 3 na kisha Surface 2) ya sanduku mstatili wa Kielelezo\(\PageIndex{2}\). Kutumia Equation 16.2.16,

\[\oint \vec{B} \cdot d\vec{s} = \mu_0 \epsilon_0 (d/dt) \int_S \vec{E} \cdot n \, da\]

kwa uso 3, na kisha uso 2, mavuno equations mbili

\[\dfrac{\partial E_y (x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_z (x,t)}{\partial t}, \label{16.18}\]

\[\dfrac{\partial B_z(x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_y (x,t)}{\partial t}. \label{16.19}\]

Equations hizi zinaelezea uwanja wa B unaotegemea anga unaozalishwa na shamba la E linalotegemea wakati.

Sisi ijayo kuchanganya equations kuonyesha kubadilisha uwanja B kuzalisha shamba E na equation kuonyesha kubadilisha E shamba kuzalisha uwanja B. Kuchukua derivative ya Equation\ ref {16.16} kuhusiana na x na kutumia Equation\ ref {16.26} anatoa

\[\dfrac{\partial^2E_y}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial E_y}{\partial x}\right) = - \dfrac{\partial}{\partial x}\left(\dfrac{\partial B_z}{\partial t}\right) = - \dfrac{\partial}{\partial t}\left(\dfrac{\partial B_z}{\partial x}\right) = \dfrac{\partial}{\partial t}\left(\epsilon_0 \mu_0 \dfrac{\partial E_y}{\partial t}\right)\]

\[\dfrac{\partial^2E_y}{\partial x^2} = \epsilon_0 \mu_0 \dfrac{\partial^2 E_y}{\partial t^2}\]

Hii ni fomu iliyochukuliwa na equation ya jumla ya wimbi kwa wimbi la ndege yetu. Kwa sababu equations kuelezea wimbi kusafiri katika baadhi kama-haijulikani kasi c, tunaweza kudhani sehemu shamba ni kila kazi ya x — ct kwa wimbi kusafiri katika x -direction, yaani,

\[E_y (x,t) = f(\xi) \, where \, \xi = x - ct. \label{16.21}\]

Imeachwa kama zoezi la hisabati kuonyesha, kwa kutumia utawala wa mnyororo kwa upambanuzi, kwamba Equations\ ref {16.17} na\ ref {16.18} inamaanisha

\[1 = \epsilon_0 \mu_0 c^2.\]

Kasi ya wimbi la umeme katika nafasi ya bure hutolewa kwa suala la upungufu na permittivity ya nafasi ya bure na

\[c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}. \label{16.22}\]

Tunaweza tu kwa urahisi kuwa na kudhani wimbi sumakuumeme na sehemu shamba\(E_z (x,t)\) na\(B_y (x,t)\). Aina hiyohiyo ya uchambuzi na Equation\ ref {16.25} na\ ref {16.24} ingeonyesha pia kwamba kasi ya wimbi la sumakuumeme ni\(c = 1/\sqrt{\epsilon_0\mu_0}\).

Fizikia ya kusafiri mashamba ya umeme ilifanywa na Maxwell mwaka 1873. Alionyesha kwa njia ya jumla zaidi kuliko derivation yetu ya kwamba mawimbi ya sumakuumeme daima husafiri katika nafasi ya bure kwa kasi iliyotolewa na Equation\ ref {16.18}. Kama sisi kutathmini kasi\(c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}\), tunaona kwamba

\[c = \dfrac{1}{\sqrt{\left(8.85 \times 10^{-12} \dfrac{C^2}{N \cdot m^2}\right)\left(4\pi \times 10^{-7} \dfrac{T \cdot m}{A}\right)}} = 3.00 \times 10^8 m/s,\]

ambayo ni kasi ya mwanga. Fikiria msisimko kwamba Maxwell lazima kuwa waliona wakati aligundua equation hii! Alikuwa amepata uhusiano wa msingi kati ya matukio mawili yanayoonekana yasiyohusiana: mashamba ya umeme na mwanga.

Zoezi\(\PageIndex{1}\)

Ulinganisho wa wimbi ulipatikana kwa (1) kutafuta shamba la E lililozalishwa na shamba la kubadilisha B, (2) kutafuta uwanja wa B uliozalishwa na shamba la kubadilisha E, na kuchanganya matokeo mawili. Ni ipi kati ya equations ya Maxwell ilikuwa msingi wa hatua (1) na ni ipi ya hatua (2)?

Jibu (hatua ya 1): Sheria ya Faraday
Jibu (hatua ya 2): sheria ya Ampère-Maxwell

Jinsi Mashamba ya E na B yanahusiana

Hadi sasa, tumeona kwamba viwango vya mabadiliko ya vipengele tofauti vya mashamba ya E na B vinahusiana, kwamba wimbi la umeme ni transverse, na kwamba wimbi linaenea kwa kasi c. Sisi ijayo tunaonyesha nini equations ya Maxwell inamaanisha kuhusu uwiano wa ukubwa wa shamba la E na B na maelekezo ya jamaa ya mashamba ya E na B.

Sasa tunazingatia ufumbuzi wa Equation\ ref {16.16} kwa namna ya mawimbi ya ndege kwa uwanja wa umeme:

\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t). \label{16.23}\]

Tumechukua wimbi kwa hiari kusafiri katika+x -mwelekeo na kuchagua awamu yake ili nguvu ya shamba ya juu hutokea kwa asili kwa wakati\(t = 0\). Sisi ni haki katika kuzingatia sines tu na cosines kwa njia hii, na kuzalisha matokeo, kwa sababu theorem ya Fourier ina maana tunaweza kueleza wimbi lolote, ikiwa ni pamoja na hata kazi za hatua za mraba, kama superposition ya sines na cosines.

Katika hatua yoyote maalum katika nafasi, uwanja E oscillates sinusoidally katika mzunguko angular\(\omega\) kati\(+E_0\) na\(-E_0\) na sawa, uwanja B oscillates kati\(+B_0\) na\(-B_0\). Amplitude ya wimbi ni thamani ya juu ya\(E_y(x,t)\). Kipindi cha oscillation T ni wakati unaohitajika kwa oscillation kamili. frequency f ni idadi ya oscillations kamili kwa kitengo cha muda, na ni kuhusiana na mzunguko angular\(\omega\) na\(\omega = 2\pi f\). Urefu wa wavelength\(\lambda\) ni umbali unaofunikwa na mzunguko mmoja kamili wa wimbi, na namba ya wimbi k ni idadi ya wavelengths inayofaa katika umbali wa\(2\pi\) katika vitengo vinavyotumiwa. Kiasi hiki kinahusiana kwa njia sawa na kwa wimbi la mitambo:

\[\omega = 2\pi f, \, \, f = \dfrac{1}{T}, \, \, k = \dfrac{2\pi}{\lambda}, \, \, and \, \, c = f\lambda = \omega/k.\]

Kutokana na kwamba suluhisho la\(E_y\) ina fomu iliyoonyeshwa katika Equation\ ref {16.20}, tunahitaji kuamua\(B\) shamba linaloambatana nayo. Kutoka Equation\ ref {16.24}, sehemu ya shamba la magnetic\(B_z\) lazima itii

\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial E_y}{\partial x}\]

\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial}{\partial x} E_0 \, \cos \, (kx - \omega t) = kE_0 \, sin\, (kx - \omega t). \label{16.24}\]

Kwa sababu suluhisho la muundo wa B -shamba la wimbi linaenea katika+x -mwelekeo kwa kasi sawa c kama muundo wa E- shamba, lazima iwe kazi ya\(k(x - ct) = kx - \omega t\). Hivyo, sisi kuhitimisha kutoka Equation\ ref {16.21} kwamba\(B_z\) ni

\[B_z(x,t) = \dfrac{k}{\omega} E_0 \, \cos \, (kx - \omega t) = \dfrac{1}{c}E_0 \, \cos \, (kx - \omega t).\]

Matokeo haya yanaweza kuandikwa kama

\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t)\]

\[B_z(x,t) = B_0 \, \cos \, (kx - \omega t) \label{16.25}\]

\[\dfrac{E_y}{B_z} = \dfrac{E_0}{B_0} = c. \label{16.26}\]

Kwa hiyo, kilele cha mashamba ya E na B sanjari, kama vile mabwawa ya wimbi, na kila hatua, mashamba ya E na B yana uwiano sawa na kasi ya mwanga c. Wimbi la ndege lina fomu iliyoonyeshwa kwenye Kielelezo\(\PageIndex{3}\).

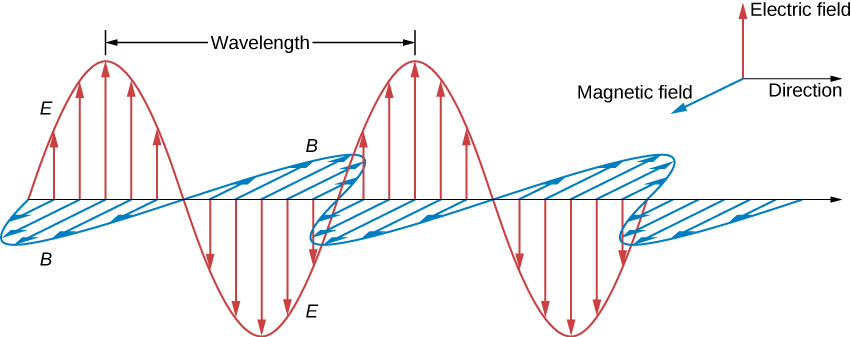
Kielelezo kinaonyesha chanya x mwelekeo kama mwelekeo wa uenezi. Mwelekeo wa y chanya umeandikwa uwanja wa umeme na mwelekeo mzuri wa z unaitwa shamba la magnetic. wimbi sine katika ndege xy ni kinachoitwa E. uwanja mishale umeme na misingi yao juu ya mhimili x na vidokezo vyao juu ya wimbi E. wimbi nyingine sine kinachoitwa B ni katika ndege xz. Mishale ya shamba la magnetic ina misingi yao kwenye mhimili x na vidokezo vyao juu ya wimbi B. mawimbi E na B yana wavelength sawa na iko katika awamu na kila mmoja. — Kielelezo\(\PageIndex{3}\): The plane wave solution of Maxwell’s equations has the B field directly proportional to the E field at each point, with the relative directions shown.

Example \(\PageIndex{1}\): Calculating B-Field Strength in an Electromagnetic Wave

What is the maximum strength of the B field in an electromagnetic wave that has a maximum E-field strength of 1000 V/m?

Strategy

To find the B-field strength, we rearrange Equation \ref{16.23} to solve for \(B\), yielding

\[B = \dfrac{E}{c}. \nonumber\]

Solution We are given E, and c is the speed of light. Entering these into the expression for B yields

\[B = \dfrac{1000 \, V/m}{3.00 \times 10^8 \, m/s} = 3.33 \times 10^{-6} T. \nonumber\]

Significance

The B-field strength is less than a tenth of Earth’s admittedly weak magnetic field. This means that a relatively strong electric field of 1000 V/m is accompanied by a relatively weak magnetic field.

Changing electric fields create relatively weak magnetic fields. The combined electric and magnetic fields can be detected in electromagnetic waves, however, by taking advantage of the phenomenon of resonance, as Hertz did. A system with the same natural frequency as the electromagnetic wave can be made to oscillate. All radio and TV receivers use this principle to pick up and then amplify weak electromagnetic waves, while rejecting all others not at their resonant frequency.

Exercise \(\PageIndex{2}\)

What conclusions did our analysis of Maxwell’s equations lead to about these properties of a plane electromagnetic wave:

the relative directions of wave propagation, of the E field, and of B field,
the speed of travel of the wave and how the speed depends on frequency, and
the relative magnitudes of the E and B fields.

Answer a: The directions of wave propagation, of the E field, and of B field are all mutually perpendicular.
Answer b: The speed of the electromagnetic wave is the speed of light \(c = 1/\sqrt{\epsilon_0\mu_0}\) independent of frequency.
Answer c: The ratio of electric and magnetic field amplitudes is \(E/B = c\).

Production and Detection of Electromagnetic Waves

A steady electric current produces a magnetic field that is constant in time and which does not propagate as a wave. Accelerating charges, however, produce electromagnetic waves. An electric charge oscillating up and down, or an alternating current or flow of charge in a conductor, emit radiation at the frequencies of their oscillations. The electromagnetic field of a dipole antenna is shown in Figure \(\PageIndex{4}\). The positive and negative charges on the two conductors are made to reverse at the desired frequency by the output of a transmitter as the power source. The continually changing current accelerates charge in the antenna, and this results in an oscillating electric field a distance away from the antenna. The changing electric fields produce changing magnetic fields that in turn produce changing electric fields, which thereby propagate as electromagnetic waves. The frequency of this radiation is the same as the frequency of the ac source that is accelerating the electrons in the antenna. The two conducting elements of the dipole antenna are commonly straight wires. The total length of the two wires is typically about one-half of the desired wavelength (hence, the alternative name half-wave antenna), because this allows standing waves to be set up and enhances the effectiveness of the radiation.

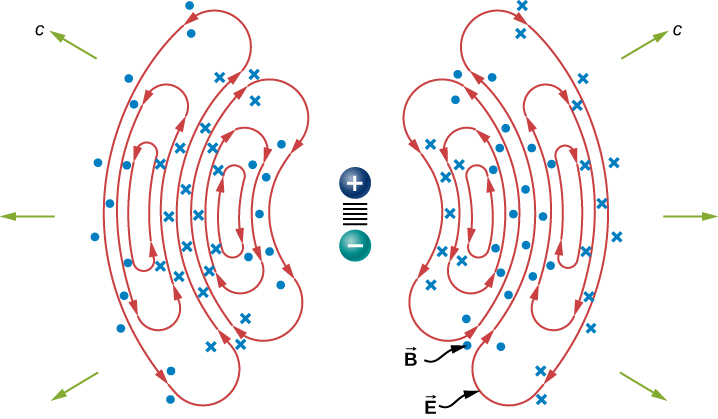
Figure shows positive and negative terminals in the centre. Surrounding this on either side are electric field loops labeled E. Magnetic field lines B are shown as dots and crosses. Arrows labeled C radiate outward. — Kielelezo\(\PageIndex{4}\): Mwendo wa oscillatory wa mashtaka katika antenna ya dipole hutoa mionzi ya umeme.

Mstari wa uwanja wa umeme katika ndege moja huonyeshwa. Sehemu ya magnetic ni perpendicular kwa ndege hii. Sehemu hii ya mionzi ina ulinganifu wa cylindrical karibu na mhimili wa dipole. Mstari wa shamba karibu na dipole hauonyeshwa. Mfano sio sare kabisa kwa pande zote. Ishara yenye nguvu iko katika mwelekeo perpendicular kwa mhimili wa antenna, ambayo itakuwa ya usawa ikiwa antenna imewekwa kwa wima. Kuna kiwango cha sifuri kando ya mhimili wa antenna. Mashamba yanayogunduliwa mbali na antenna yanatoka kwenye mashamba ya umeme na magnetic yanayobadilishana na kusafiri kama mawimbi ya sumakuumeme. Mbali na antenna, mipaka ya wimbi, au nyuso za awamu sawa kwa wimbi la umeme, ni karibu spherical. Hata mbali na antenna, mionzi huenea kama mawimbi ya ndege ya umeme.

Mawimbi ya sumakuumeme hubeba nishati mbali na chanzo chao, sawa na wimbi la sauti linalobeba nishati mbali na wimbi lililosimama kwenye kamba ya gitaa. Antenna ya kupokea ishara za umeme hufanya kazi kwa reverse. Mawimbi ya umeme yanayoingia husababisha mikondo ya oscillating katika antenna, kila mmoja kwa mzunguko wake mwenyewe. Mpokeaji wa redio ni pamoja na mzunguko wa tuner, ambao mzunguko wa resonant unaweza kubadilishwa. Tuner hujibu sana kwa mzunguko uliotaka lakini sio wengine, kuruhusu mtumiaji kutazama matangazo yaliyohitajika. Vipengele vya umeme huongeza ishara inayotengenezwa na elektroni zinazohamia. Ishara hiyo inabadilishwa kuwa muundo wa sauti na/au video.

Kumbuka

Kutumia simulation hii kutangaza mawimbi ya redio. Wiggle elektroni transmita manually au kuwa ni oscillate moja kwa moja. Onyesha shamba kama pembe au vectors. Chati ya mstari inaonyesha nafasi za elektroni kwenye mtoaji na kwenye mpokeaji.