14.5: Mzunguko wa RL
- Page ID
- 176354
Mwishoni mwa sehemu hii, utaweza:
- Kuchambua nyaya zilizo na inductor na kupinga katika mfululizo
- Eleza jinsi ya sasa na voltage exponentially kukua au kuoza kulingana na hali ya awali
Mzunguko na upinzani na kujitegemea hujulikana kama mzunguko wa RL. Kielelezo\(\PageIndex{1a}\) kinaonyesha mzunguko wa RL unao na kupinga, inductor, chanzo cha mara kwa mara cha emf, na swichi\(S_1\) na\(S_2\). Wakati\(S_1\) imefungwa, mzunguko huo ni sawa na mzunguko mmoja wa kitanzi unao na kupinga na inductor iliyounganishwa kwenye chanzo cha emf (Kielelezo\(\PageIndex{1b}\)). Wakati\(S_1\) unafunguliwa na\(S_2\) kufungwa, mzunguko unakuwa mzunguko wa kitanzi kimoja na kupinga tu na inductor (Kielelezo\(\PageIndex{1c}\)).
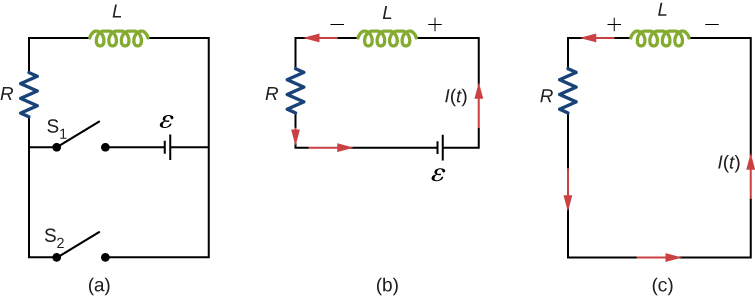
Sisi kwanza tunazingatia mzunguko wa RL wa Kielelezo\(\PageIndex{1b}\). Mara baada\(S_1\) ya\(S_2\) kufungwa na kufunguliwa, chanzo cha emf hutoa sasa katika mzunguko. Ikiwa hapakuwa na inductance binafsi katika mzunguko, sasa ingeongezeka mara moja kwa thamani ya kutosha ya\(\epsilon/R\). Hata hivyo, kutokana na sheria ya Faraday, sasa kuongezeka hutoa emf\(V_L = -L(dI/dt)\) katika inductor. Kwa mujibu wa sheria ya Lenz, emf iliyosababishwa inakabiliana na ongezeko la sasa na inaongozwa kama inavyoonekana katika takwimu. Matokeo yake,\(I(t)\) huanza saa sifuri na huongezeka kwa thamani ya mwisho kwa thamani yake ya mwisho.
Kutumia utawala wa kitanzi cha Kirchhoff kwenye mzunguko huu, tunapata
\[\epsilon - L\dfrac{dI}{dt} - IR = 0, \label{eq1}\]
ambayo ni ya kwanza ili tofauti equation kwa\(I(t)\). Angalia kufanana kwake na equation kwa capacitor na kupinga katika mfululizo (angalia RC Circuits). Vile vile, suluhisho la Equation\ ref {eq1} linaweza kupatikana kwa kufanya mbadala katika milinganyo inayohusiana na capacitor kwa inductor. Hii inatoa
\[ \begin{align} I(t) &= \dfrac{\epsilon}{R}(1 - e^{-Rt/L}) \\[4pt] &= \dfrac{\epsilon}{R}(1 - e^{-t/\tau_L}),\label{eq3} \end{align}\]
wapi
\[\tau_L = L/R \label{eq5}\]
ni mara kwa mara ya mara kwa mara ya mzunguko.
Ya sasa\(I(t)\) imepangwa katika Kielelezo\(\PageIndex{2a}\). Inaanza saa sifuri, na kama\(t \rightarrow \infty\),\(I(t)\)\(\epsilon/R\) inakaribia kwa urahisi. Emf ikiwa\(V_L(t)\) ni moja kwa moja sawia na\(dI/dt\), au mteremko wa curve. Kwa hiyo, wakati wa ukubwa wake mara baada ya swichi kutupwa, emf ikiwa inapungua kwa sifuri kwa wakati kama sasa inakaribia thamani yake ya mwisho ya\(\epsilon/R\). Mzunguko huo unakuwa sawa na kupinga kushikamana kwenye chanzo cha emf.
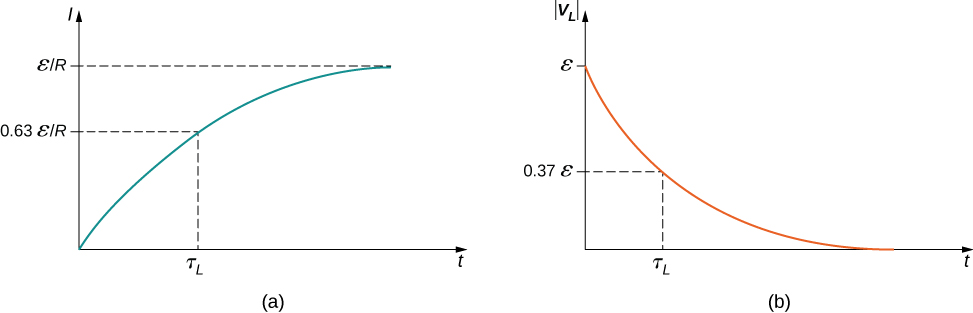
Nishati iliyohifadhiwa katika uwanja wa magnetic wa inductor ni
\[U_L = \dfrac{1}{2}LI^2.\]
Kwa hiyo, kama sasa inakaribia kiwango cha juu cha sasa\(\epsilon/R\), nishati iliyohifadhiwa katika inductor huongezeka kutoka sifuri na haipatikani kwa kiwango cha juu\(L(\epsilon/R)^2 /2\).
Wakati wa mara kwa mara\(\tau_L\) unatuambia jinsi kasi ya sasa inavyoongezeka kwa thamani yake ya mwisho. Katika\(t = \tau_L\), sasa katika mzunguko ni, kutoka Equation\ ref {eq3},
\[I(\tau_L) = \dfrac{\epsilon}{R}(1 - e^{-1}) = 0.63 \dfrac{\epsilon}{R},\]
ambayo ni\(63\%\) ya mwisho\(\epsilon/R\). Kidogo cha muda wa kuingiza mara kwa mara\(\tau_L = L/R\), mbinu za sasa za haraka zaidi\(\epsilon/R\).
Tunaweza kupata utegemezi wa muda wa voltage ikiwa katika inductor katika mzunguko huu kwa kutumia\(V_L(t) = -L(dI/dt)\) na Equation\ ref {eq3}:
\[V_L(t) = -L\dfrac{dI}{dt} = -\epsilon e^{-t/\tau_L}.\]
Ukubwa wa kazi hii imepangwa katika Kielelezo\(\PageIndex{2b}\). Thamani kubwa ya\(L(dI/dt)\) ni\(\epsilon\); hutokea wakati\(dI/dt\) ni kubwa, ambayo ni mara baada ya\(S_1\) kufungwa na\(S_2\) kufunguliwa. Katika njia ya hali ya kutosha,\(dI/dt\) hupungua hadi sifuri. Matokeo yake, voltage katika inductor pia hutoweka kama\(t \rightarrow \infty\).
Wakati wa mara kwa mara\(\tau_L\) pia unatuambia jinsi ya haraka kuoza kwa voltage. Kwa ukubwa\(t = \tau_L\) wa voltage ikiwa ni
\[|V_L(\tau_L)| = \epsilon e^{-1} = 0.37 \epsilon = 0.37 V(0).\]
Kwa hiyo voltage katika inductor inashuka hadi juu\(37\%\) ya thamani yake ya awali baada ya mara kwa mara mara. Muda mfupi wa mara kwa mara\(\tau_L\), kasi zaidi voltage inapungua.
Baada ya muda wa kutosha umepita ili sasa imefikia thamani yake ya mwisho, nafasi za swichi katika Kielelezo\(\PageIndex{1a}\) zinabadilishwa, kutupa mzunguko katika sehemu (c). Katika\(t = 0\), sasa katika mzunguko ni\(I(0) = \epsilon/R\). Kwa utawala wa kitanzi cha Kirchhoff, tunapata
\[IR + L\dfrac{dI}{dt} = 0.\]
Suluhisho la equation hii ni sawa na suluhisho la equation kwa capacitor kuruhusu, na mbadala sawa. Ya sasa kwa wakati t ni basi
\[I(t) = \dfrac{\epsilon}{R}e^{-t/\tau_L}.\]
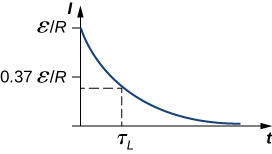
Ya sasa huanza\(I(0) = \epsilon/R\) na inapungua kwa wakati kama nishati iliyohifadhiwa katika inductor imefutwa (Kielelezo\(\PageIndex{3}\)).
Utegemezi wa wakati wa voltage katika inductor unaweza kuamua kutoka\(V_L = -L(dI/dt)\):
\[V_L(0) = \epsilon e^{-t/\tau_L}. \label{14.32}\]
Voltage hii ni ya awali\(V_L(0) = \epsilon\), na inaharibika hadi sifuri kama ya sasa. Nishati iliyohifadhiwa katika uwanja wa magnetic ya inductor\(LI^2/2\), pia inapungua kwa muda kwa muda, kwa kuwa inaharibiwa na joto la Joule katika upinzani wa mzunguko.
Katika mzunguko wa Kielelezo\(\PageIndex{1a}\), basi\(\epsilon = 2.0 \, V, \, R = 4.0 \, \Omega\), na\(L = 4.0 \, H\). Kwa\(S_1\) kufungwa na\(S_2\) kufunguliwa (Kielelezo\(\PageIndex{1b}\)), (a) ni wakati gani wa mzunguko? (b) Ni nini sasa katika mzunguko na ukubwa wa emf ikiwa katika inductor saa\(t = 0,\) saa\(t = 2.0 \tau_L\), na kama\(t \rightarrow \infty\)?
Mkakati
Muda wa mara kwa mara kwa inductor na kupinga katika mzunguko wa mfululizo huhesabiwa kwa kutumia Equation\ ref {eq5}. Ya sasa kupitia na voltage katika inductor ni mahesabu na matukio ya kina kutoka Equation\ ref {eq3} na Equation\ ref {14.32}.
Suluhisho
- Mara kwa mara ya mara kwa mara ni\[\tau_L = \dfrac{L}{R} = \dfrac{4.0 \, H}{4.0 \, \Omega} = 1.0 \, s.\]
- Ya sasa katika mzunguko wa Kielelezo\(\PageIndex{1b}\) huongezeka kulingana na Equation\ ref {eq3}:\[I(t) = \dfrac{\epsilon}{R}(1 - e^{-t/\tau_L}). \nonumber\]\[(1 - e^{-t/\tau_L}) = (1 - 1) = 0; \, so \, I(0) = 0. \nonumber\] Katika\(t = 0\), Katika\(t = 2.0 \tau_L\) na\(t \rightarrow \infty\), tuna, kwa mtiririko huo,\[I(2.0\tau_L) = \dfrac{\epsilon}{R}(1 - e^{-2.0}) = (0.50 \, A)(0.86) = 0.43 \, A \nonumber\] na\[I(\infty) = \dfrac{\epsilon}{R} = 0.50 \, A. \nonumber\] Kutoka Equation\ ref {14.32}, ukubwa wa emf ikiwa huharibika kama\[|V_L(t)| = \epsilon e^{-t/\tau_L}. \nonumber\] At\(t = 0\), \(t = 2.0 \tau_L\), na kama\(t \rightarrow \infty\), sisi kupata\[|V_L(0)| = \epsilon = \, V,\]\[|V_L(2.0 \tau_L)| = (2.0 \, V) e^{-2.0} = 0.27 \, V\] na\[|V_L(\infty)| = 0.\nonumber\]
Umuhimu
Ikiwa wakati wa kipimo ulikuwa mkubwa zaidi kuliko mara kwa mara, hatuwezi kuona kuoza au ukuaji wa voltage katika inductor au resistor. Mzunguko ungefikia haraka maadili yasiyo ya kawaida kwa haya yote (Kielelezo\(\PageIndex{4}\)).
Baada ya sasa katika mzunguko wa RL wa Mfano\(\PageIndex{1}\) umefikia thamani yake ya mwisho, nafasi za swichi zinabadilishwa ili mzunguko uwe ule ulioonyeshwa kwenye Mchoro\(\PageIndex{1c}\).
- Inachukua muda gani sasa kushuka kwa nusu thamani yake ya awali?
- Inachukua muda gani kabla ya nishati iliyohifadhiwa katika inductor imepungua hadi thamani yake\(1.0 \%\) ya juu?
Mkakati
Ya sasa katika inductor sasa itapungua kama kupinga dissipates nishati hii. Kwa hiyo, sasa huanguka kama kuoza kwa maonyesho. Tunaweza pia kutumia uhusiano huo kama badala ya nishati katika formula inductor ili kujua jinsi nishati inapungua kwa vipindi tofauti wakati.
Suluhisho
- Pamoja na swichi kuachwa, sasa itapungua kulingana\[I(t) = \dfrac{\epsilon}{R}e^{-t/\tau_L} = I(0)e^{-t/\tau_L}.\nonumber\] na Wakati t wakati sasa ni nusu thamani yake ya awali, tuna\[I(t) = 0.50 I(0)\space so \, e^{-t/\tau_L} = 0.50,\nonumber\] na\[t = -[\ln(0.50)]\tau_L = 0.69 (1.0 \, s) = 0.69 \, s\nonumber\] ambapo tumetumia inductive wakati mara kwa mara kupatikana katika Mfano\(\PageIndex{1}\).
- Nishati iliyohifadhiwa katika inductor inapewa na\[U_L(t) = \dfrac{1}{2}L[I(t)]^2 = \dfrac{1}{2}L\left(\dfrac{\epsilon}{R} e^{-t/\tau_L}\right)^2 = \dfrac{L\epsilon^2}{2R^2}e^{-2t/\tau_L}.\nonumber\] Ikiwa nishati inapungua kwa thamani yake\(1.0\%\) ya awali kwa wakati t, tuna\[U_L(t) = (0.010)U_L(0) \, or \, \dfrac{L\epsilon^2}{2R^2} e^{-2t/\tau_L} = (0.010)\dfrac{L\epsilon^2}{2R^2}.\nonumber\] Baada ya kufuta maneno na kuchukua logarithm ya asili ya pande zote mbili, tunapata\[-\dfrac{2t}{\tau_L} = \ln(0.010),\] hivyo\[t = -\dfrac{1}{2} \tau_L \ln(0.010).\nonumber\] Tangu\(\tau_L = 1.0 \, s\), wakati unachukua nishati kuhifadhiwa katika inductor kupungua kwa thamani yake\(1.0\%\) ya awali ni\[t = -\dfrac{1}{2}(1.0 \, s)\ln(0.010) = 2.3 \, s.\nonumber\]
Umuhimu
Hesabu hii inafanya kazi tu ikiwa mzunguko una kiwango cha juu cha sasa katika hali (b) kabla ya hali hii mpya. Vinginevyo, tunaanza na sasa ya chini ya awali, ambayo itaharibika kwa uhusiano huo.
Thibitisha kwamba RC na L/R zina vipimo vya muda
- Ikiwa sasa katika mzunguko wa Kielelezo\(\PageIndex{1b}\) huongezeka hadi thamani yake\(90\%\) ya mwisho baada ya 5.0 s, ni nini wakati wa kuingiza mara kwa mara?
- Ikiwa\(R = 20 \, \Omega\), ni thamani gani ya kujitegemea?
- Ikiwa\(R = 20 \, \Omega\) kupinga inabadilishwa na\(R = 100 \, \Omega\) kupinga, ni wakati gani unachukuliwa kwa sasa kufikia thamani yake\(90\%\) ya mwisho?
- Jibu
-
a. 2.2 s; b. 43 H; c. 1.0 s
Kwa mzunguko wa katika Kielelezo\(\PageIndex{1b}\), onyesha kwamba wakati hali ya kutosha imefikiwa, tofauti katika nguvu za jumla zinazozalishwa na betri na zimeharibika katika kupinga ni sawa na nishati iliyohifadhiwa katika uwanja wa magnetic wa coil


