14.4: Nishati katika uwanja wa Magnetic

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza jinsi nishati inaweza kuhifadhiwa katika uwanja wa magnetic
• Kupata equation kwa ajili ya nishati kuhifadhiwa katika cable Koaxial, kutokana na wiani magnetic nishati

Nishati ya capacitor imehifadhiwa katika uwanja wa umeme kati ya sahani zake. Vile vile, inductor ina uwezo wa kuhifadhi nishati, lakini katika uwanja wake wa magnetic. Nishati hii inaweza kupatikana kwa kuunganisha wiani wa nishati magnetic,

\[u_m = \dfrac{B^2}{2\mu_0}\]

juu ya kiasi sahihi. Ili kuelewa wapi fomu hii inatoka, hebu tuchunguze solenoid ya muda mrefu, ya cylindrical ya sehemu iliyopita. Tena kwa kutumia usio solenoid makadirio, tunaweza kudhani kwamba shamba magnetic kimsingi ni mara kwa mara na kutolewa na\(B = \mu_0 nI\) kila mahali ndani ya solenoid. Hivyo, nishati iliyohifadhiwa katika solenoid au kiasi cha wiani wa nishati ya magnetic ni sawa na

\[U = u_m(V) = \dfrac{(\mu_0nI)^2}{2\mu_0}(Al) = \dfrac{1}{2}(\mu_0n^2Al)I^2. \label{14.19}\]

Pamoja na badala ya Equation 14.3.12, hii inakuwa

\[\boxed{U = \dfrac{1}{2}LI^2.}\]

Ingawa inayotokana na kesi maalum, equation hii inatoa nishati kuhifadhiwa katika uwanja magnetic ya inductor yoyote. Tunaweza kuona hili kwa kuzingatia inductor ya kiholela kwa njia ambayo sasa ya kubadilisha inapita. Kwa papo yoyote, ukubwa wa emf ikiwa ni\(\epsilon = Ldi/dt\), ambapo i ni sasa ikiwa katika mfano huo. Kwa hiyo, nguvu kufyonzwa na inductor ni

\[P = \epsilon i = L\dfrac{di}{dt}i.\]

Nishati ya jumla iliyohifadhiwa kwenye uwanja wa magnetic wakati ongezeko la sasa kutoka 0 hadi mimi kwa muda kutoka 0 hadi t inaweza kuamua kwa kuunganisha maneno haya:

\[U = \int_0^t Pdt' = \int_0^t L\dfrac{di}{dt'}idt' = L\int_0^l idi = \dfrac{1}{2}LI^2. \label{14.22}\]

Mfano\(\PageIndex{1}\): Self-Inductance of a Coaxial Cable

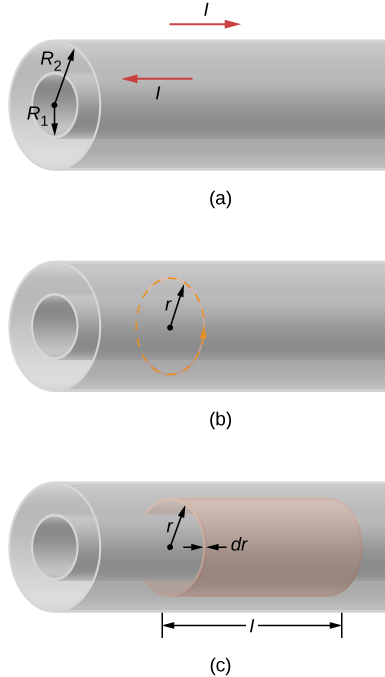
Kielelezo\(\PageIndex{1}\) kinaonyesha shells mbili za muda mrefu, za cylindrical za radii\(R_1\) na\(R_2\). Kama ilivyojadiliwa katika Capitance juu ya capacitance, usanidi huu ni uwakilishi rahisi wa cable coaxial. Capitance kwa urefu wa kitengo cha cable tayari imehesabiwa. Sasa (a) kuamua nishati ya magnetic iliyohifadhiwa kwa urefu wa kitengo cha cable coaxial na (b) tumia matokeo haya ili kupata inductance binafsi kwa urefu wa kitengo cha cable.

Kielelezo\(\PageIndex{1}\): (a) Cable coaxial inawakilishwa hapa na mbili mashimo, conductors centric cylindrical ambayo sasa umeme inapita katika pande tofauti. (b) Uwanja wa magnetic kati ya waendeshaji unaweza kupatikana kwa kutumia sheria ya Ampère kwenye njia iliyopigwa. (c) Shell ya cylindrical hutumiwa kupata nishati ya magnetic iliyohifadhiwa kwa urefu l ya cable.

Mkakati

Sehemu ya magnetic ndani na nje ya cable coaxial imedhamiriwa na sheria ya Ampère. Kulingana na uwanja huu wa magnetic, tunaweza kutumia Equation\ ref {14.22} kuhesabu wiani wa nishati ya shamba la magnetic. Nishati ya magnetic inahesabiwa na sehemu muhimu ya wiani wa nishati ya magnetic mara kiasi tofauti juu ya shell cylindrical. Baada ya ushirikiano unafanywa, tuna suluhisho la fomu iliyofungwa kwa sehemu (a). Self-inductance kwa urefu wa kitengo imedhamiriwa kulingana na matokeo haya na Equation\ ref {14.22}.

Suluhisho

1. Tunaamua shamba la magnetic kati ya waendeshaji kwa kutumia sheria ya Ampère kwenye njia ya mviringo iliyopigwa iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1b}\). Kwa sababu ya ulinganifu cylindrical,\(\vec{B}\) ni mara kwa mara katika njia, na\[\oint \vec{B} \cdot d\vec{l} = B(2\pi r) = \mu_0 I.\] hii inatupa\[B = \dfrac{\mu_0I}{2\pi r}. \nonumber\] Katika kanda nje cable, maombi sawa ya sheria Ampère inaonyesha kwamba\(B = 0\), kwa kuwa hakuna sasa wavu misalaba eneo imepakana na njia ya mviringo ambapo\(r > R_2\). Hoja hii pia inashikilia wakati\(r < R_1\); yaani, katika kanda ndani ya silinda ya ndani. Nishati zote za magnetic za cable zinahifadhiwa kati ya waendeshaji wawili. Kwa kuwa wiani wa nishati ya shamba la magnetic ni\[u_m = \dfrac{B^2}{2\mu_0}\nonumber\] nishati iliyohifadhiwa katika shell ya cylindrical ya radius ya ndani r, radius ya nje\(r + dr\) na urefu l (angalia sehemu (c) ya takwimu) ni\[u_m = \dfrac{\mu_0I^2}{8\pi^2 r^2}.\nonumber\] Hivyo, nishati ya jumla ya shamba la magnetic katika urefu l ya cable ni\[U = \int_{R_1}^{R_2} dU = \int_{R_1}^{R_2} \dfrac{\mu_0I^2}{8\pi^2r^2}(2\pi rl)dr = \dfrac{\mu_0I^2l}{4\pi} ln \dfrac{R_2}{R_1},\nonumber\] na nishati kwa urefu wa kitengo ni\((\mu_0I^2 / 4\pi)ln(R_2/R_1).\)
2. Kutoka Equation\ ref {14.22},\[U = \dfrac{1}{2}LI^2,\] ambapo L ni inductance binafsi ya urefu l ya cable coaxial. Kulinganisha equations mbili zilizopita, tunaona kwamba kujitegemea kwa urefu wa kitengo cha cable ni\[\dfrac{L}{l} = \dfrac{\mu_0}{2\pi}\ln\dfrac{R_2}{R_1}.\nonumber\]

Umuhimu

Inductance kwa urefu wa kitengo inategemea tu radii ya ndani na nje kama inavyoonekana katika matokeo. Ili kuongeza inductance, tunaweza kuongeza radius ya nje (\(R_2\)) au kupunguza radius ya ndani (\(R_1\)). Katika kikomo kama radii mbili zinakuwa sawa, inductance inakwenda sifuri. Katika kikomo hiki, hakuna cable coaxial. Pia, nishati ya magnetic kwa urefu wa kitengo kutoka sehemu (a) ni sawa na mraba wa sasa.

Zoezi\(\PageIndex{1}\)

Ni kiasi gani cha nishati kinachohifadhiwa katika inductor ya Mfano 14.3.1 baada ya sasa kufikia thamani yake ya juu?

Suluhisho

0.50 M