12.A: Vyanzo vya Magnetic Fields (Majibu)
- Page ID
- 175788
Angalia Uelewa Wako
12.1. Mita 1.41
12.2. \(\displaystyle \frac{μ_0I}{2R}\)
12.3. 4 amps inapita nje ya ukurasa
12.4. Wote wana nguvu kwa kila kitengo urefu wa\(\displaystyle 9.23×10^{−12}N/m\)
12.5. Mita 0.608
12.6. Katika kesi hizi integrals kuzunguka kitanzi Ampèrian ni vigumu sana kwa sababu hakuna ulinganifu, hivyo njia hii ingekuwa na manufaa.
12.7. a. 1.00382;
b. 1.00015
12.8. a\(\displaystyle 1.0×10^{−4}T\);.
b. 0.60 T;
c.\(\displaystyle 6.0×10^3\)
Maswali ya dhana
1. Faida ya sheria ya Biot-Savart ni kwamba inafanya kazi na shamba lolote la magnetic zinazozalishwa na kitanzi cha sasa. Hasara ni kwamba inaweza kuchukua muda mrefu.
3. Ikiwa ungeenda mwanzo wa sehemu ya mstari na uhesabu angle\(\displaystyle θ\) kuwa takriban\(\displaystyle 0°\), waya inaweza kuchukuliwa kuwa usio na kipimo. Hukumu hii ni msingi pia juu ya usahihi unahitaji katika matokeo.
5. Ungependa kuhakikisha mikondo inapita perpendicular kwa kila mmoja.
7. Mstari wa shamba la magnetic hutoa mwelekeo wa shamba la magnetic wakati wowote katika nafasi. Uzito wa mistari ya magnetic shamba inaonyesha nguvu ya shamba la magnetic.
9. spring inapunguza kwa urefu tangu kila coil na kuwa na kaskazini pole zinazozalishwa magnetic shamba karibu na pole kusini ya coil ya.
11. Sheria ya Ampère ni halali kwa njia zote zilizofungwa, lakini si muhimu kwa kuhesabu mashamba wakati uwanja wa magnetic zinazozalishwa unakosa ulinganifu ambao unaweza kutumiwa na uchaguzi mzuri wa njia.
13. Ikiwa hakuna sasa ndani ya kitanzi, hakuna shamba la magnetic (angalia sheria ya Ampère). Nje ya bomba, kunaweza kuwa na sasa iliyofungwa kupitia bomba la shaba, hivyo shamba la magnetic haliwezi kuwa sifuri nje ya bomba.
15. Sumaku ya bar itakuwa sumaku mbili, kila mmoja na miti yao ya kaskazini na kusini. Hakuna monopoles magnetic au sumaku moja pole.
Matatizo
17. \(\displaystyle 5.66×10^{−5}T\)
19. \(\displaystyle B=\frac{μ_oI}{8}(\frac{1}{a}−\frac{1}{b})\)nje ya ukurasa
21. \(\displaystyle a=\frac{2R}{π}\); sasa katika waya kwa haki lazima inapita kati ya ukurasa.
23. 20 A
25. Wote majibu na ukubwa wa uwanja magnetic ya\(\displaystyle 4.5×10^{−5}T\).
27. Katika P1, uwanja wa magnetic wavu ni sifuri. Katika P2,\(\displaystyle B=\frac{3μ_oI}{8πa}\) kwenye ukurasa.
29. Shamba la magnetic ni kiwango cha chini kwa umbali na waya wa juu, au nusu ya njia kati ya waya.
31. a.\(\displaystyle F/l=8×10^{−6}\) N/m mbali na waya mwingine;
b.\(\displaystyle F/l=8×10^{−6}\) N/m kuelekea waya mwingine
33. \(\displaystyle B=\frac{μ_oIa}{2πb^2}\)katika ukurasa
35. 0.019 m
37. \(\displaystyle 6.28×10^{−5}T\)
39. \(\displaystyle B=\frac{\mu_{o} I R^{2}}{\left(\left(\frac{d}{2}\right)^{2}+R^{2}\right)^{3 / 2}}\)
41. a.\(\displaystyle μ0I;\)
b. 0;
c\(\displaystyle μ0I\);
d. 0
43. a\(\displaystyle 3μ_0I\);.
b. 0;
c\(\displaystyle 7μ_0I\);
d.\(\displaystyle −2μ_0I\)
45. katika radius R
47.
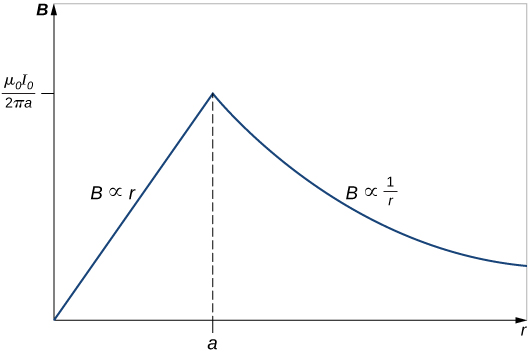
49. \(\displaystyle B=1.3×10^{−2}T\)
51. takriban nane zamu kwa cm
53. \(\displaystyle B=\frac{1}{2}μ_0nI\)
55. 0.0181 A
57. 0.0008 T
59. 317.31
61. \(\displaystyle 2.1×10^{−4}A⋅m^2\)\(\displaystyle 2.7A\)
63. 0.18 T
Matatizo ya ziada
65. \(\displaystyle B=6.93×10^{−5}T\)
67. \(\displaystyle 3.2×10^{−19}N\)katika arc mbali na waya
69. a. juu na chini\(\displaystyle B=μ_0j\), katikati\(\displaystyle B=0\);
b. juu na chini\(\displaystyle B=0\), katikati\(\displaystyle B=μ_0j\)
71. \(\displaystyle \frac{dB}{B}=−\frac{dr}{r}\)
73. a. 52778 zamu;
b. 0.10 T
75. \(\displaystyle B_1(x)=\frac{μ_0IR^2}{2(R^2+z^2)^{3/2}}\)
77. \(\displaystyle B=\frac{μ_0σω}{2}R\)
79. chimbuko
81. chimbuko
83. Kama umbali wa radial unakwenda kwa infinity, mashamba ya magnetic ya kila formulae haya huenda sifuri.
85. a\(\displaystyle B=\frac{μ_0I}{2πr}\);.
b.\(\displaystyle B=\frac{μ_0J_0r^2}{3R}\)
87. \(\displaystyle B(r)=μ_0NI/2πr\)
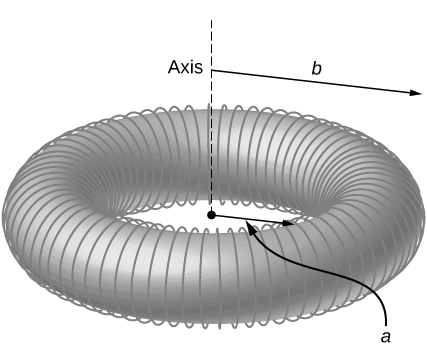
Changamoto Matatizo
89. \(\displaystyle B=\frac{μ_0I}{2πx}\).
91. a\(\displaystyle B=\frac{μ_0σω}{2}[\frac{2h^2+R^2}{\sqrt{R^2+h^0}}]\);.
b.\(\displaystyle B=4.09×10^{−5}T\), 82% ya shamba la magnetic duniani


