12.7: Solenoids na Toroids
- Page ID
- 175866
Mwishoni mwa sehemu hii, utaweza:
- Kuanzisha uhusiano kwa jinsi shamba magnetic ya solenoid inatofautiana na umbali na sasa kwa kutumia sheria zote za Biot-Savart na sheria ya Ampère
- Kuanzisha uhusiano kwa jinsi shamba magnetic ya toroid inatofautiana na umbali na sasa kwa kutumia sheria ya Ampère
Vifaa viwili vya kawaida na muhimu vya umeme huitwa solenoids na toroids. Kwa namna moja au nyingine, ni sehemu ya vyombo vingi, vikubwa na vidogo. Katika sehemu hii, tunachunguza uwanja wa magnetic mfano wa vifaa hivi.
Solenoids
Jeraha la waya mrefu kwa namna ya coil ya helical inajulikana kama solenoid. Solenoids hutumiwa kwa kawaida katika utafiti wa majaribio wanaohitaji mashamba ya magnetic. Solenoid kwa ujumla ni rahisi upepo, na karibu na kituo chake, shamba lake la magnetic ni sare kabisa na moja kwa moja sawa na sasa katika waya.
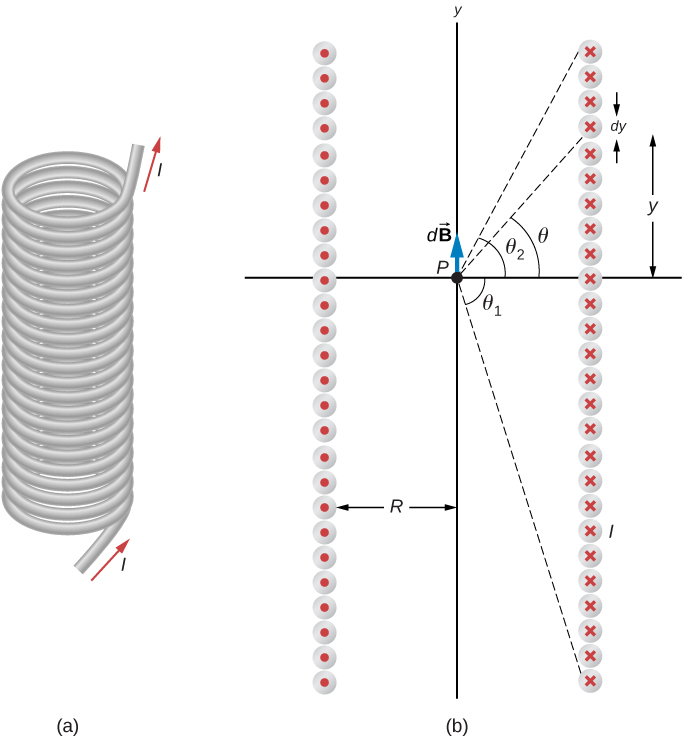
Kielelezo\(\PageIndex{1}\) kinaonyesha solenoid yenye N zamu ya waya tightly jeraha juu ya urefu L. Sasa mimi inapita kwenye waya wa solenoid. Idadi ya zamu kwa urefu wa kitengo ni N/L; kwa hiyo, idadi ya zamu katika dy ya urefu usio na kipimo ni (N/L) inarudi. Hii inazalisha sasa
\[dI = \frac{NI}{L} dy. \label{12.24}\]
Sisi kwanza kuhesabu shamba magnetic katika hatua P ya Kielelezo\(\PageIndex{1}\). Hatua hii iko kwenye mhimili wa kati wa solenoid. Sisi ni kimsingi kukata solenoid katika vipande nyembamba kwamba ni kavu nene na kutibu kila kama kitanzi sasa. Hivyo, Di ni sasa kupitia kila kipande. Sehemu ya magnetic\(d\vec{B}\) kutokana na Di ya sasa katika dy inaweza kupatikana kwa msaada wa Equation 12.5.3 na Equation\ ref {12.24}:
\[d\vec{B} = \frac{\mu_0 R^2 dI}{2(y^2 + R^2)^{3/2}}\hat{j} = \left( \frac{\mu_0 IR^2 N}{2L}\hat{j}\right) \frac{dy}{(y^2 + R^2)^{3/2}} \label{12.25}\]
ambapo tulitumia Equation\ ref {12.24} kuchukua nafasi ya di. Shamba la matokeo katika P linapatikana kwa kuunganisha\(d\vec{B}\) urefu wote wa solenoid. Ni rahisi kutathmini hii muhimu kwa kubadilisha tofauti ya kujitegemea kutoka y hadi\(\theta\). Kutoka ukaguzi wa Kielelezo\(\PageIndex{1}\), tuna:
\[sin \, \theta = \frac{y}{\sqrt{y^2 + R^2}}.\label{12.26}\]
Kuchukua tofauti ya pande zote mbili za equation hii, tunapata
\[cos \, \theta \, d\theta = \left[ - \frac{y^2}{(y^2 + R^2)^{3/2}} + \frac{1}{\sqrt{y^2 + R^2}}\right] dy \]
\[ = \frac{R^2 dy}{(y^2 + R^2)^{3/2}}.\]
Wakati hii ni kubadilishwa katika equation kwa\(d\vec{B}\), tuna
\[\vec{B} = \frac{\mu_0 I N}{2L}\hat{j} \int_{\theta_1}^{\theta_2} cos \, \theta \, d\theta = \frac{\mu_0 I N}{2L} (sin \, \theta_2 - sin \, \theta_1)\hat{j}, \label{12.27}\]
ambayo ni uwanja wa magnetic pamoja na mhimili wa kati wa solenoid ya mwisho.
Ya maslahi maalum ni solenoid ya muda mrefu sana, ambayo\(L \rightarrow \infty\). Kutoka kwa mtazamo wa vitendo, solenoid isiyo na kipimo ni moja ambayo urefu wake ni mkubwa zaidi kuliko radius yake\((L >> R)\). Katika kesi hii,\(\theta_1 = \frac{-\pi}{2}\) na\(\theta_2 = \frac{\pi}{2}\). Kisha kutoka Equation\ ref {12.27}, shamba magnetic pamoja mhimili kati ya solenoid usio na mwisho ni
\[\vec{B} = \frac{\mu_0 IN}{2L} \hat{j} [sin(\pi/2) - sin(-\pi/2)] = \frac{\mu_0 IN}{L} \hat{j}\]au
\[\vec{B} = \mu_0 n I \hat{j}, \label{12.28}\]
ambapo n ni idadi ya zamu kwa urefu wa kitengo. Unaweza kupata mwelekeo wa utawala wa mkono wa\(\vec{B}\) kulia: Curl vidole vyako kwa uongozi wa sasa, na pointi zako za kidole kwenye uwanja wa magnetic katika mambo ya ndani ya solenoid.
Sasa tunatumia mali hizi, pamoja na sheria ya Ampère, kuhesabu ukubwa wa shamba la magnetic mahali popote ndani ya solenoid isiyo na kipimo. Fikiria njia iliyofungwa ya Kielelezo\(\PageIndex{2}\). Pamoja sehemu ya 1,\(\vec{B}\) ni sare na sambamba na njia. Pamoja na makundi ya 2 na 4,\(\vec{B}\) ni perpendicular kwa sehemu ya njia na hutoweka juu ya mapumziko yake. Kwa hiyo, makundi ya 2 na 4 hayachangia mstari muhimu katika sheria ya Ampère. Pamoja na sehemu ya 3,\(\vec{B} = 0\) kwa sababu shamba la magnetic ni sifuri nje ya solenoid. Ikiwa unazingatia sheria ya Ampère ya kitanzi nje ya solenoid, sasa inapita kwa njia tofauti kwenye makundi tofauti ya waya. Kwa hiyo, hakuna sasa iliyoambatanishwa na hakuna shamba la magnetic kulingana na sheria ya Ampère. Hivyo, hakuna mchango wa mstari muhimu kutoka sehemu ya 3. Matokeo yake, tunaona
\[\oint \vec{B} \cdot d\vec{l} = \int_1 \vec{B} \cdot d\vec{l} = Bl. \label{12.29}\]
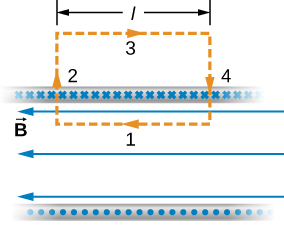
solenoid ina n zamu kwa kitengo urefu, hivyo sasa kwamba hupita kwa njia ya uso iliyoambatanishwa na njia ni NLi. Kwa hiyo, kutokana na sheria ya Ampère,
\[Bl = \mu_0 n lI\]na
\[B = \mu_0 n I \label{12.30}\]
ndani ya solenoid. Hii inakubaliana na kile tulichopata mapema kwa B kwenye mhimili wa kati wa solenoid. Hapa, hata hivyo, eneo la sehemu ya 1 ni holela, hivyo tumegundua kwamba equation hii inatoa shamba magnetic kila mahali ndani ya solenoid usio.
Nje ya solenoid, mtu anaweza kuteka kitanzi cha sheria ya Ampère karibu na solenoid nzima. Hii ingekuwa enclose sasa inapita katika pande zote mbili. Kwa hiyo, sasa ya wavu ndani ya kitanzi ni sifuri. Kwa mujibu wa sheria ya Ampère, ikiwa sasa ya wavu ni sifuri, uwanja wa magnetic lazima uwe sifuri. Kwa hiyo, kwa maeneo nje ya radius ya solenoid, shamba la magnetic ni sifuri.
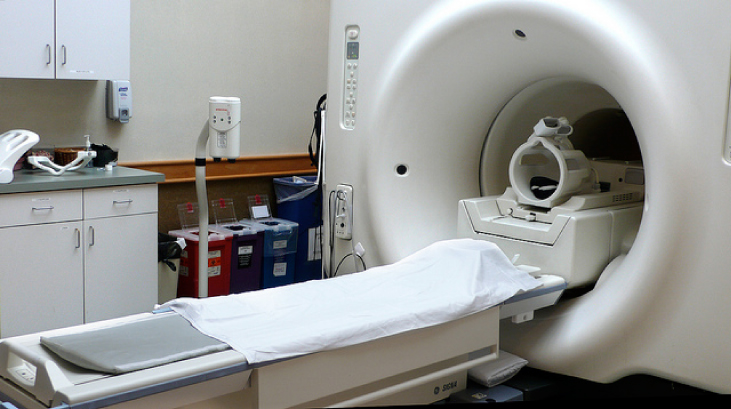
Wakati mgonjwa anapopata uchunguzi wa magnetic resonance (MRI), mtu hulala kwenye meza inayohamishwa katikati ya solenoid kubwa ambayo inaweza kuzalisha mashamba makubwa ya magnetic. Solenoid ina uwezo wa mashamba haya ya juu kutoka kwa mikondo ya juu inayozunguka kupitia waya za juu. Sehemu kubwa ya magnetic hutumiwa kubadili spin ya protons katika mwili wa mgonjwa. Muda unachukua kwa spins kuunganisha au kupumzika (kurudi kwenye mwelekeo wa awali) ni saini ya tishu tofauti ambazo zinaweza kuchambuliwa ili kuona kama miundo ya tishu ni ya kawaida (Kielelezo\(\PageIndex{3}\)).
Solenoid ina zamu 300 zamu kuzunguka silinda ya kipenyo 1.20 cm na urefu 14.0 cm. Ikiwa sasa kupitia coils ni 0.410 A, ni ukubwa gani wa shamba la magnetic ndani na karibu katikati ya solenoid?
Mkakati
Tunapewa idadi ya zamu na urefu wa solenoid ili tuweze kupata idadi ya zamu kwa urefu wa kitengo. Kwa hiyo, uwanja wa magnetic ndani na karibu katikati ya solenoid hutolewa na Equation\ ref {12.30}. Nje ya solenoid, shamba la magnetic ni sifuri.
Suluhisho
Idadi ya zamu kwa urefu wa kitengo ni
\[n = \frac{300 \, turns}{0.140 \, m} = 2.14 \times 10^3 \, turns/m.\]
Sehemu ya magnetic zinazozalishwa ndani ya solenoid ni
\[B = \mu_0 nI = (4\pi \times 10^{-7} T \cdot m/A)(2.14 \times 10^3 turns/m)(0.410 \, A)\]
\[B = 1.10 \times 10^{-3}T.\]
Umuhimu
Suluhisho hili halali tu ikiwa urefu wa solenoid ni kubwa sana ikilinganishwa na kipenyo chake. Mfano huu ni kesi ambapo hii halali.
ni uwiano wa uwanja magnetic zinazozalishwa kutoka kwa kutumia formula finite juu ya makadirio usio kwa angle\(\theta\) ya (a)\(85^o\) nini? (b)\(89^o\)? Solenoid ina 1000 inarudi katika cm 50 na sasa ya 1.0 A inapita kupitia coils
- Suluhisho
-
a. 1.00382; b. 1.00015
Toroids
A toroid ni coil donut-umbo karibu jeraha na waya moja kuendelea, kama inavyoonekana katika sehemu (a) ya Kielelezo\(\PageIndex{4}\). Ikiwa toroid ina N windings na sasa katika waya ni mimi, ni shamba la magnetic ndani na nje ya toroid?
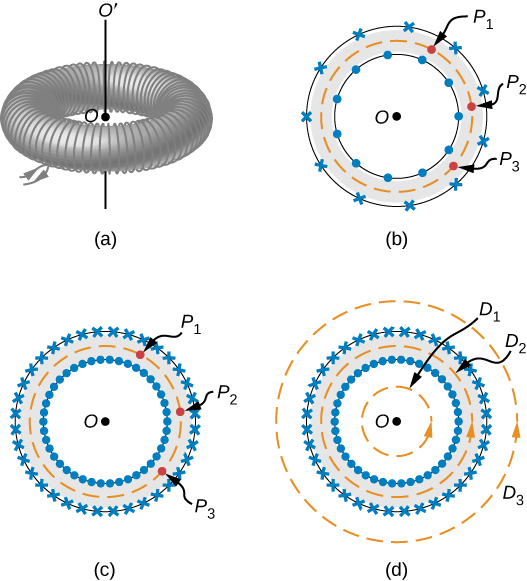
Tunaanza kwa kuchukua ulinganifu wa cylindrical karibu na mhimili OO '. Kwa kweli, dhana hii si usahihi sahihi, kwa kama sehemu (b) ya Kielelezo\(\PageIndex{4}\) inaonyesha, mtazamo wa coil toroidal inatofautiana kutoka hatua kwa hatua (kwa mfano,\(P_1, \, P_2\) na\(P_3\)) juu ya njia ya mviringo unaozingatia karibu OO '. Hata hivyo, kama toroid ni tightly jeraha, pointi zote kwenye mduara kuwa kimsingi sawa [sehemu (c) ya Kielelezo\(\PageIndex{4}\)], na ulinganifu cylindrical ni makadirio sahihi.
Kwa ulinganifu huu, shamba la magnetic lazima liwe tangent na mara kwa mara katika ukubwa pamoja na njia yoyote ya mviringo unaozingatia OO '. Hii inaruhusu sisi kuandika kwa kila njia\(D_1, \, D_2\) na\(D_3\) inavyoonekana katika sehemu (d) ya Kielelezo\(\PageIndex{4}\),
\[\oint \vec{B} \cdot d\vec{l} = B(2\pi r). \label{12.31}\]
Sheria ya Ampère inahusiana hii muhimu kwa sasa ya wavu inayopitia uso wowote unaofungwa na njia ya ushirikiano. Kwa njia ambayo ni nje ya toroid, ama hakuna sasa inapita kupitia uso unaozunguka (njia\(D_1\)), au sasa inayopita kupitia uso katika mwelekeo mmoja ni sawa na sasa inayopita kwa njia hiyo kinyume (njia\(D_3\)). Katika hali yoyote, hakuna sasa wavu kupita kwa njia ya uso, hivyo
\[\oint B(2\pi r) = 0\]na
\[B = 0 \, (outside \, the \, toroid). \label{12.32}\]
Zamu za toroid huunda helix, badala ya loops za mviringo. Matokeo yake, kuna shamba ndogo nje ya coil; hata hivyo, derivation hapo juu ina kama coils walikuwa mviringo.
Kwa njia ya mviringo ndani ya toroid (njia\(D_2\)), sasa katika waya hupunguza uso N mara, na kusababisha ni ya sasa ya sasa kupitia uso. Sasa tunapata na sheria ya Ampère,
\[B(2\pi r) = \mu_0 NI\]na
\[B = \frac{\mu_0 NI}{2\pi r} \, (within \, the \, toroid). \label{12.33}\]
Shamba la magnetic linaelekezwa katika mwelekeo wa kinyume cha saa kwa windings iliyoonyeshwa. Wakati sasa katika coils inabadilishwa, mwelekeo wa shamba la magnetic pia hurudi.
Sehemu ya magnetic ndani ya toroid si sare, kwani inatofautiana inversely na umbali r kutoka mhimili OO '. Hata hivyo, ikiwa radius ya kati R (radius katikati ya radii ya ndani na nje ya toroid) ni kubwa zaidi kuliko kipenyo cha msalaba wa coil r, tofauti ni ndogo sana, na ukubwa wa shamba la magnetic inaweza kuhesabiwa kwa Equation\ ref {12.33} ambapo \(r = R\).


