12.6: Sheria ya Ampère
- Page ID
- 175794
Mwishoni mwa sehemu hii, utaweza:
- Eleza jinsi sheria ya Ampère inahusiana na uwanja wa magnetic zinazozalishwa na sasa kwa thamani ya sasa
- Tumia shamba la magnetic kutoka kwa waya mrefu wa moja kwa moja, ama nyembamba au nene, kwa sheria ya Ampère
Mali ya msingi ya shamba la magnetic tuli ni kwamba, tofauti na shamba la umeme, sio kihafidhina. Shamba la kihafidhina ni moja linalofanya kiasi sawa cha kazi kwenye chembe inayohamia kati ya pointi mbili tofauti bila kujali njia iliyochaguliwa. Mashamba ya magnetic hayana mali kama hiyo. Badala yake, kuna uhusiano kati ya uwanja wa magnetic na chanzo chake, umeme wa sasa. Ni walionyesha katika suala la mstari muhimu wa\(\vec{B}\) na inajulikana kama sheria Ampère ya. Sheria hii pia inaweza inayotokana moja kwa moja kutoka sheria ya Biot-Savart. Sasa tunazingatia kuwa derivation kwa kesi maalum ya waya usio na kipimo, sawa.
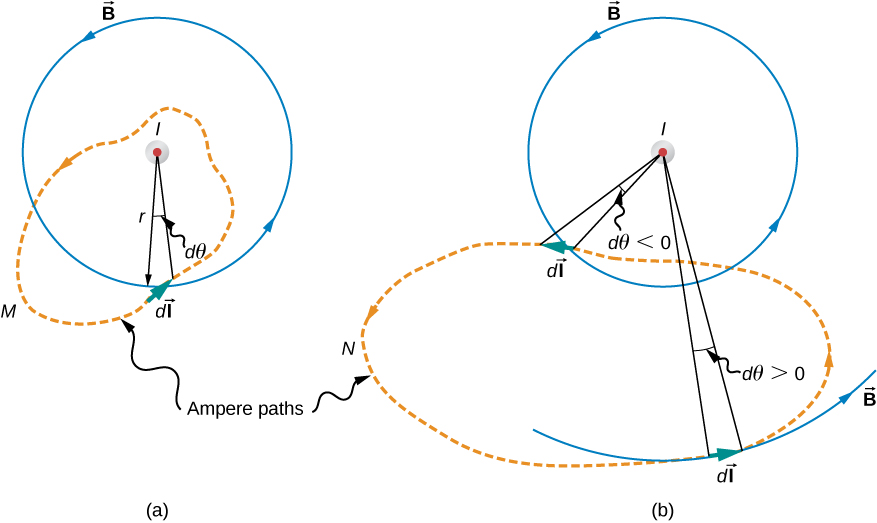
Kielelezo\(\PageIndex{1}\) kinaonyesha ndege ya kiholela perpendicular kwa waya usio na kipimo, sawa ambao sasa mimi huelekezwa nje ya ukurasa. Mistari ya shamba la magnetic ni miduara iliyoelekezwa kinyume na saa na inazingatia waya. Kuanza, hebu tuchunguze\(\oint \vec{B} \cdot d\vec{l}\) juu ya njia zilizofungwa M na N. Angalia kwamba njia moja (M) inafunga waya, wakati mwingine (N) haifai. Kwa kuwa mistari shamba ni mviringo,\(\vec{B} \cdot d\vec{l}\) ni bidhaa ya B na makadirio ya DL kwenye mduara kupita kwa njia ya\(d\vec{l}\). Ikiwa radius ya mduara huu ni r, makadirio ni\(rd\theta\), na
\[\vec{B} \cdot d\vec{l} = Br \, d\theta.\]
Pamoja na\(\vec{B}\) kutolewa na Equation 12.4.1,
\[\oint \vec{B} \cdot d\vec{l} = \oint \left(\frac{\mu_0 I}{2\pi r}\right) \, r \, d\theta = \frac{\mu_0 I}{2\pi} \oint d\theta.\]
Kwa njia M, ambayo huzunguka waya,\(\oint_M d\theta = 2\pi\) na
\[\oint_M \vec{B} \cdot d\vec{l} = \mu_0 I.\]
Njia N, kwa upande mwingine, huzunguka kwa njia zote mbili (kinyume chake) na hasi (clockwise)\(d\theta\) (angalia Mchoro\(\PageIndex{1}\)), na kwa kuwa imefungwa,\(\oint_N d\theta = 0\). Hivyo kwa njia N,
\[\oint_N \vec{B} \cdot d\vec{l} = 0.\]
Ugani wa matokeo haya kwa kesi ya jumla ni sheria ya Ampère.
Juu ya njia ya kufungwa kiholela,
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I\]
ambapo mimi ni jumla ya sasa kupita kupitia uso wowote wazi S ambao mzunguko ni njia ya ushirikiano. Maji tu ndani ya njia ya ushirikiano yanahitaji kuchukuliwa.
Kuamua kama sasa maalum mimi ni chanya au hasi, curl vidole vya mkono wako wa kulia katika mwelekeo wa njia ya ushirikiano, kama inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kama mimi hupita kupitia S katika mwelekeo sawa na thumb yako kupanuliwa, Mimi ni chanya; kama mimi hupita kwa njia ya S katika mwelekeo kinyume na thumb yako kupanuliwa, ni hasi.
Ili kuhesabu shamba la magnetic linaloundwa kutoka kwa sasa kwenye waya (s), tumia hatua zifuatazo:
- Tambua ulinganifu wa sasa katika waya (s). Ikiwa hakuna ulinganifu, tumia sheria ya Biot-Savart kuamua shamba la magnetic.
- Kuamua mwelekeo wa shamba la magnetic linaloundwa na waya (s) na utawala wa mkono wa kulia 2.
- Chagua kitanzi cha njia ambapo uwanja wa magnetic ni ama mara kwa mara au sifuri.
- Tumia sasa ndani ya kitanzi.
- Tumia mstari muhimu\(\oint \vec{B} \cdot d\vec{l}\) karibu na kitanzi kilichofungwa.
- Equate\(\oint \vec{B} \cdot d\vec{l}\)\(\mu_0 I_{enc}\) na\(\mu_0 I_{enc}\) na kutatua kwa\(\vec{B}\).
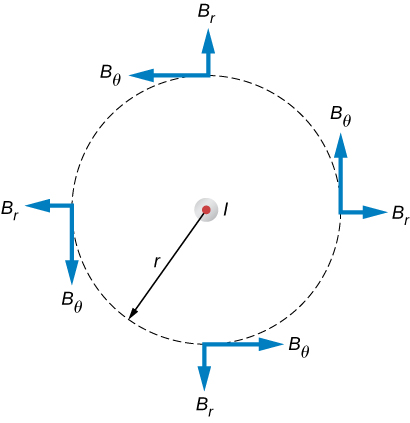
Tumia sheria ya Ampère kuhesabu shamba la magnetic kutokana na sasa ya kutosha mimi katika waya usio na muda mrefu, nyembamba, sawa kama inavyoonekana kwenye Kielelezo\(\PageIndex{2}\).
Mkakati
Fikiria ndege ya kiholela perpendicular kwa waya, na sasa iliyoongozwa nje ya ukurasa. inawezekana sehemu magnetic shamba katika ndege hii,\(B_r\) na\(B_{\theta}\) ni umeonyesha katika pointi holela juu ya mduara wa r Radius unaozingatia waya. Kwa kuwa shamba ni cylindrically symmetric,\(B_r\) wala\(B_{\theta}\) hutofautiana na nafasi kwenye mduara huu. Pia kutokana na ulinganifu, mistari ya radial, ikiwa iko, inapaswa kuelekezwa ama ndani au nje kutoka kwa waya. Hii inamaanisha, hata hivyo, kwamba kuna lazima iwe na flux ya magnetic ya wavu katika silinda ya kiholela inayozingatia waya. Sehemu ya radial ya shamba la magnetic lazima iwe sifuri kwa sababu\(\vec{B}_r \cdot d\vec{l} = 0\). Kwa hiyo, tunaweza kutumia sheria ya Ampère kwenye njia ya mviringo kama inavyoonekana.
Suluhisho
Zaidi ya njia hii\(\vec{B}\) ni mara kwa mara na sambamba na\(d\vec{l}\), hivyo
\[\oint \vec{B} \cdot d\vec{l} = B_{\theta} \oint dl = B_{\theta}(2\pi r).\]
Hivyo sheria ya Ampère inapunguza
\[B_{\theta}(2\pi r) = \mu_0 I.\]
Hatimaye, tangu\(B_{\theta}\) ni sehemu tu ya\(\vec{B}\), tunaweza kuacha Subscript na kuandika
\[B = \frac{\mu_0 I}{2\pi r}.\]
Hii inakubaliana na hesabu ya Biot-Savart hapo juu.
Umuhimu
Sheria ya Ampère inafanya kazi vizuri ikiwa una njia ya kuunganisha juu ya ambayo\(\vec{B} \cdot d\vec{l}\) ina matokeo ambayo ni rahisi kurahisisha. Kwa waya usio, hii inafanya kazi kwa urahisi na njia ambayo ni mviringo kuzunguka waya ili shamba magnetic sababu nje ya ushirikiano. Ikiwa utegemezi wa njia unaonekana ngumu, unaweza kurudi kwenye sheria ya Biot-Savart na kutumia hiyo ili kupata shamba la magnetic.
Radi ya waya mrefu, sawa ya Kielelezo\(\PageIndex{3}\) ni, na waya hubeba sasa\(I_0\) ambayo inasambazwa kwa usawa juu ya sehemu yake ya msalaba. Pata shamba la magnetic ndani na nje ya waya.
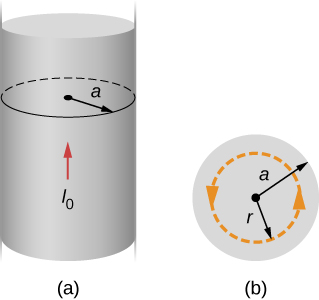
Mkakati
Tatizo hili lina jiometri sawa na Mfano\(\PageIndex{1}\), lakini iliyoambatanishwa sasa mabadiliko kama sisi hoja njia ya ushirikiano kutoka nje ya waya ndani ya waya, ambapo haina kukamata nzima sasa iliyoambatanishwa (angalia Kielelezo\(\PageIndex{3}\)).
Suluhisho
Kwa njia yoyote ya mviringo ya r radius kwamba ni katikati ya waya,
\[\oint \vec{B} \cdot d\vec{l} = \oint Bdl = B\oint dl = B(2\pi r).\]
Kutokana na sheria ya Ampère, hii inalingana na jumla ya sasa inayopitia uso wowote unaofungwa na njia ya ushirikiano.
Fikiria kwanza njia ya mviringo ambayo ni ndani ya waya kama\((r \leq a)\) vile ile inavyoonekana katika sehemu (a) ya Kielelezo\(\PageIndex{3}\). Tunahitaji sasa mimi kupita katika eneo iliyoambatanishwa na njia. Ni sawa na wiani wa sasa J mara eneo lililofungwa. Kwa kuwa sasa ni sare, wiani wa sasa ndani ya njia ni sawa na wiani wa sasa katika waya nzima, ambayo ni\(I_0 / \pi a^2\). Kwa hiyo, sasa mimi kupita katika eneo iliyoambatanishwa na njia ni
\[I = \frac{\pi r^2}{\pi a^2} I_0 = \frac{r^2}{a^2}I_0.\]
Tunaweza kuzingatia uwiano huu kwa sababu wiani wa sasa J ni mara kwa mara juu ya eneo la waya. Kwa hiyo, wiani wa sasa wa sehemu ya waya ni sawa na wiani wa sasa katika eneo lote. Kutumia sheria ya Ampère, tunapata
\[B(2\pi r) = \mu_0 \left(\frac{r^2}{a^2}\right) I_0,\]
na shamba la magnetic ndani ya waya ni
\[B = \frac{\mu_0 I_0}{2\pi} \frac{r}{a^2} (r \leq a).\]
Nje ya waya, hali hiyo inafanana na ile ya waya usio na mwisho wa mfano uliopita; yaani,
\[B = \frac{\mu_0 I_0}{2\pi r} (r \geq a).\]
Tofauti ya B na r inavyoonekana kwenye Kielelezo\(\PageIndex{4}\).
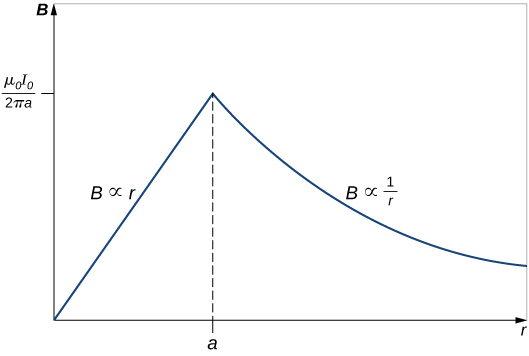
Umuhimu
Matokeo yanaonyesha kuwa kama umbali wa radial unavyoongezeka ndani ya waya mwembamba, shamba la magnetic huongezeka kutoka sifuri hadi thamani ya kawaida ya uwanja wa magnetic wa waya nyembamba. Nje ya waya, shamba linatoka bila kujali ikiwa ni waya mwembamba au nyembamba.
Matokeo haya ni sawa na jinsi sheria ya Gauss kwa mashtaka ya umeme yanavyofanya ndani ya usambazaji wa malipo sare, isipokuwa kwamba sheria ya Gauss kwa mashtaka ya umeme ina usambazaji wa kiasi sare ya malipo, ilhali sheria ya Ampère hapa ina eneo sare la usambazaji wa sasa. Pia, kuacha nje ya waya mwembamba ni sawa na jinsi uwanja wa umeme unavyoanguka nje ya usambazaji wa malipo ya mstari, kwani kesi hizo mbili zina jiometri sawa na hakuna kesi inategemea usanidi wa mashtaka au mikondo mara kitanzi kiko nje ya usambazaji.
Matumizi sheria Ampère ya kutathmini\(\oint \vec{B} \cdot d\vec{l}\) kwa usanidi wa sasa na njia katika Kielelezo\(\PageIndex{5}\).
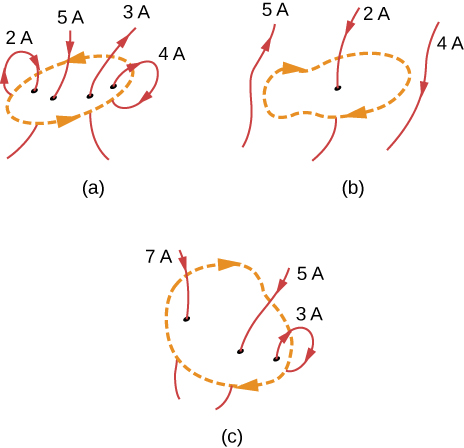
Mkakati
Sheria ya Ampère inasema kwamba\(\oint \vec{B} \cdot d\vec{l} = \mu_0 I\) ambapo mimi ni jumla ya sasa kupita katika kitanzi iliyoambatanishwa. Njia ya haraka ya kutathmini muhimu ni kuhesabu\(\mu_0 I\) kwa kutafuta sasa ya wavu kupitia kitanzi. Maji mazuri yanapita kati ya kidole chako cha kulia ikiwa vidole vyako vinapiga karibu na mwelekeo wa kitanzi. Hii itatuambia ishara ya jibu.
Suluhisho
(a) sasa kwenda kushuka kwa njia ya kitanzi sawa sasa kwenda nje ya kitanzi, hivyo sasa wavu ni sifuri. Hivyo,\(\oint \vec{B} \cdot d\vec{l} = 0.\)
(b) sasa tu ya kuzingatia katika tatizo hili ni 2A kwa sababu ni sasa tu ndani ya kitanzi. Utawala wa mkono wa kulia unatuonyesha sasa kwenda chini kupitia kitanzi ni katika mwelekeo mzuri. Kwa hiyo, jibu ni\(\oint \vec{B} \cdot d\vec{l} = \mu_0 (2 \, A) = 2.51 \times 10^{-6} T \cdot m.\)
(c) Utawala wa mkono wa kulia unatuonyesha sasa kwenda chini kupitia kitanzi ni katika mwelekeo mzuri. Kuna\(7A + 5A = 12 A\) ya sasa kwenda kushuka na -3 kwenda zaidi. Kwa hiyo, jumla ya sasa ni 9 A na\(\oint \vec{B} \cdot d\vec{l} = \mu_0 (9 \, A) = 5.65 \times 10^{-6} T \cdot m\).
Umuhimu
Ikiwa mikondo yote yamefungwa ili sasa hiyo iliingia kwenye kitanzi na nje ya kitanzi, sasa ya wavu itakuwa sifuri na hakuna shamba la magnetic litakuwapo. Hii ndiyo sababu waya ni karibu sana kwa kila mmoja katika kamba ya umeme. mikondo inapita kuelekea kifaa na mbali na kifaa katika waya sawa sifuri jumla mtiririko wa sasa kupitia kitanzi Ampère kuzunguka waya hizi. Kwa hiyo, hakuna mashamba ya magnetic yaliyopotea yanaweza kuwepo kutoka kwa kamba zinazobeba sasa.
Fikiria kutumia sheria ya Ampère kuhesabu mashamba ya magnetic ya waya wa mwisho wa moja kwa moja na wa kitanzi cha mviringo cha waya. Kwa nini sio muhimu kwa mahesabu haya?
- Jibu
-
Katika kesi hizi integrals kuzunguka kitanzi Ampèrian ni vigumu sana kwa sababu hakuna ulinganifu, hivyo njia hii ingekuwa na manufaa.


