12.3: Uwanja wa Magnetic kutokana na Wire Nyembamba

Last updated
Save as PDF

Page ID: 175828

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza jinsi sheria ya Biot-Savart inatumiwa kuamua shamba la magnetic kutokana na waya nyembamba, sawa.
Kuamua utegemezi wa shamba la magnetic kutoka kwa waya nyembamba, sawa kulingana na umbali kutoka kwao na sasa inapita kwenye waya.
Piga shamba la magnetic lililoundwa kutoka kwenye waya nyembamba, sawa kwa kutumia utawala wa pili wa mkono wa kulia.

Ni kiasi gani cha sasa kinachohitajika ili kuzalisha shamba muhimu la magnetic, labda kama nguvu kama shamba la Dunia? Wafanyabiashara watakuambia kwamba mistari ya umeme ya juu huunda mashamba ya magnetic ambayo huingilia kati masomo yao ya dira. Hakika, wakati Oersted aligundua mwaka wa 1820 kwamba sasa katika waya iliathiri sindano ya dira, hakuwa na kushughulika na mikondo kubwa sana. Je! Sura ya waya inayobeba sasa inaathiri sura ya shamba la magnetic linaloundwa? Tulibainisha katika Sura ya 28 kwamba kitanzi cha sasa kiliunda uwanja wa magnetic sawa na ule wa sumaku ya bar, lakini vipi kuhusu waya moja kwa moja? Tunaweza kutumia sheria ya Biot-Savart kujibu maswali haya yote, ikiwa ni pamoja na kuamua uwanja wa magnetic wa waya mrefu wa moja kwa moja.

Kielelezo\(\PageIndex{1}\) kinaonyesha sehemu ya waya mrefu sana, moja kwa moja ambayo hubeba sasa I. Je, ni shamba la magnetic katika hatua P, iko umbali R kutoka waya?

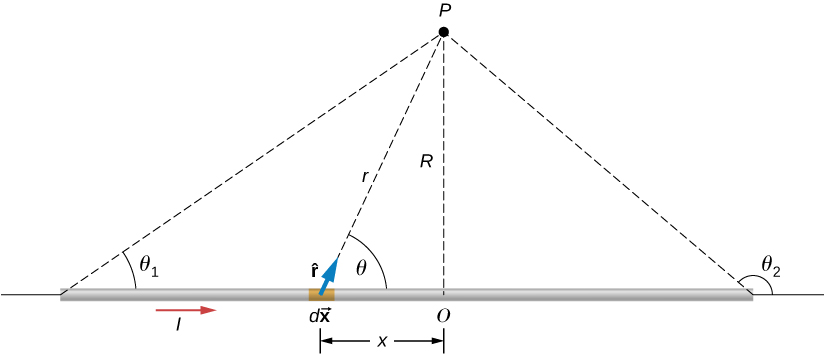
Takwimu hii inaonyesha sehemu ya waya nyembamba, moja kwa moja ya sasa ya kubeba. Point P iko umbali R kutoka katikati ya waya O na umbali r kutoka kipande cha waya Dx. Vector r kutoka kipande cha waya Dx hadi hatua P huunda theta ya angle na waya. — Kielelezo\(\PageIndex{1}\): Sehemu ya waya nyembamba, sawa ya sasa ya kubeba. Variable huru\(\theta\) ina mipaka\(\theta_1\) na\(\theta_2\).

Hebu tuanze kwa kuzingatia shamba la magnetic kutokana na kipengele cha sasa\(I \, d\vec{x}\) kilicho kwenye nafasi x. Kutumia utawala wa mkono wa kulia 1 kutoka sura ya awali,\(d\vec{x} \times \hat{r}\) inaonyesha nje ya ukurasa kwa kipengele chochote kando ya waya. Kwa hiyo\(P\), mashamba ya magnetic kutokana na mambo yote ya sasa yana mwelekeo sawa. Hii ina maana kwamba tunaweza kuhesabu shamba wavu huko kwa kutathmini jumla ya scalar ya michango ya vipengele. Pamoja na

\[|d\vec{x} \times \hat{r}| = (dx)(1) \, \sin \, \theta \]

tuna kutoka sheria ya Biot-Savart

\[B = \dfrac{\mu_0}{4\pi} \int_{wire} \dfrac{I \, \sin \, \theta \, dx}{r^2}. \label{BSLaw}\]

Waya ni symmetrical kuhusu hatua\(O\), hivyo tunaweza kuweka mipaka ya ushirikiano kutoka sifuri kwa infinity na mara mbili jibu, badala ya kuunganisha kutoka infinity hasi kwa infinity chanya. Kulingana na picha na trigonometry, tunaweza kuandika maneno\(r\) na\(\sin \, \theta\) kwa suala la x na R, yaani:

\[r = \sqrt{x^2 + R^2}\]

\[\sin \, \theta = \dfrac{R}{\sqrt{x^2 + R^2}}.\]

Kubadilisha maneno haya katika Equation\ ref {BSlaw}, ushirikiano wa shamba la magnetic unakuwa

\[B = \dfrac{\mu_0I}{2\pi} \int_0^{\infty} \dfrac{R \, dx}{(x^2 + R^2)^{3/2}}.\]

Kutathmini mavuno muhimu

\[B = \dfrac{\mu_0I}{2\pi R} \left[\dfrac{x}{(x^2 + R^2)^{1/2}}\right]_0^{\infty}.\]

Kubadilisha mipaka inatupa suluhisho

\[\boxed{B = \dfrac{\mu_0 I}{2\pi R}.}\]

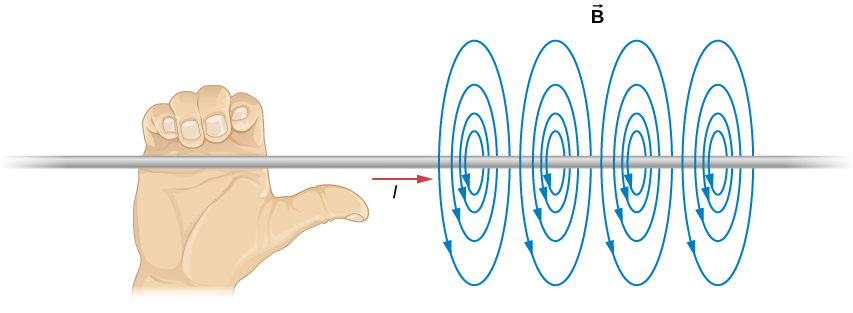
Mstari wa shamba la magnetic wa waya usio na mwisho ni mviringo na unaozingatia waya (Kielelezo\(\PageIndex{2}\)), na ni sawa katika kila ndege perpendicular kwa waya. Kwa kuwa shamba linapungua kwa umbali kutoka kwa waya, nafasi ya mistari ya shamba inapaswa kuongezeka kwa usawa na umbali. Mwelekeo wa uwanja huu wa magnetic unaweza kupatikana kwa fomu ya pili ya utawala wa mkono wa kulia (Kielelezo\(\PageIndex{2}\)). Ikiwa unashikilia waya kwa mkono wako wa kuume ili kidole chako kando ya sasa, kisha vidole vyako vifungia karibu na waya kwa maana sawa na\(\vec{B}\).

Takwimu hii inaonyesha utawala wa mkono wa kulia. Waya unafanyika kwa mkono wa kuume ili kidole kiweke kando ya sasa. Vidole vifunga karibu na waya kwa maana sawa na shamba la magnetic. — Kielelezo\(\PageIndex{2}\):. Baadhi ya mistari ya shamba la magnetic ya waya usio na kipimo. Mwelekeo wa\(B\) unaweza kupatikana kwa fomu ya utawala wa mkono wa kulia.

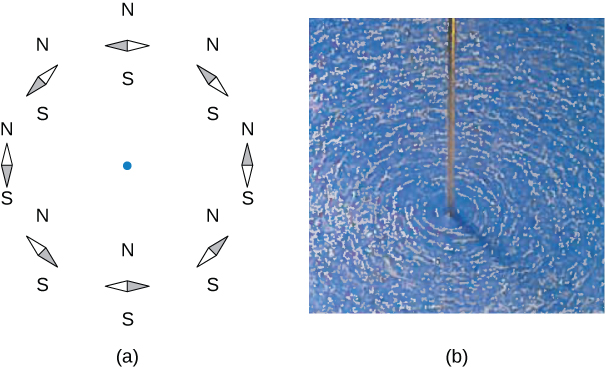
Mwelekeo wa mistari ya shamba unaweza kuzingatiwa kwa majaribio kwa kuweka sindano kadhaa ndogo za dira kwenye mduara karibu na waya, kama ilivyoonyeshwa kwenye Mchoro\(\PageIndex{3a}\). Wakati hakuna sasa katika waya, sindano zinafanana na uwanja wa magnetic wa Dunia. Hata hivyo, wakati sasa kubwa inapelekwa kupitia waya, sindano za dira zote zinaonyesha tangent kwenye mduara. Vipande vya chuma vinavyotengenezwa kwenye uso usio na usawa pia hufafanua mistari ya shamba, kama inavyoonekana kwenye Kielelezo\(\PageIndex{3b}\).

Kielelezo A kinaonyesha mduara ulioundwa na sindano ndogo za dira iliyokaa na uwanja wa magnetic wa Dunia. Kielelezo B kinaonyesha kwamba filings ya chuma iliyochapwa kwenye uso usio na usawa karibu na waya mrefu hufafanua mistari ya shamba. — Kielelezo\(\PageIndex{3}\): Sura ya mistari ya shamba la magnetic ya waya mrefu inaweza kuonekana kwa kutumia (a) sindano ndogo za dira na (b) filings za chuma.

Mfano\(\PageIndex{1}\): Calculating Magnetic Field Due to Three Wires

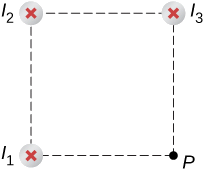
Wiring tatu hukaa kwenye pembe za mraba, mikondo yote ya kubeba ya amps 2 kwenye ukurasa kama inavyoonekana kwenye Mchoro\(\PageIndex{4}\). Tumia ukubwa wa shamba la magnetic kwenye kona nyingine ya mraba, kumweka P, ikiwa urefu wa kila upande wa mraba ni cm 1.

Kielelezo kinaonyesha waya tatu I1, I2, na I3 na sasa inapita ndani ya ukurasa. Wiring huunda pembe tatu za mraba. Sehemu ya magnetic imedhamiriwa kwenye kona ya nne ya mraba inayoitwa P. — Kielelezo\(\PageIndex{4}\): Waya tatu zina sasa zinazoingia kwenye ukurasa. Sehemu ya magnetic imedhamiriwa kwenye kona ya nne ya mraba.

Mkakati

Shamba la magnetic kutokana na kila waya kwenye hatua inayotakiwa ni mahesabu. Umbali wa diagonal umehesabiwa kwa kutumia theorem ya Pythagorean. Kisha, mwelekeo wa mchango wa kila shamba la magnetic unatambuliwa kwa kuchora mduara unaozingatia hatua ya waya na nje kuelekea hatua inayotakiwa. Mwelekeo wa mchango wa shamba la magnetic kutoka kwa waya hiyo ni tangential kwa pembe. Hatimaye, kufanya kazi na wadudu hawa, matokeo ni mahesabu.

Suluhisho

Wiring 1 na 3 wote wana ukubwa sawa wa mchango wa shamba la magnetic katika hatua P:

\[B_1 = B_3 = \dfrac{\mu_0 I}{2\pi R} = \dfrac{(4\pi \times 10^{-7} T \cdot m/A)(2 \, A)}{2\pi (0.01 \, m)} = 4 \times 10^{-5}T.\]

Waya 2 ina umbali mrefu na mchango magnetic shamba katika hatua P ya:

\[B_2 = \dfrac{\mu_0 I}{2\pi R} = \dfrac{(4\pi \times 10^{-7}T \cdot m/A)(2 \, A)}{2 \pi (0.01414 \, m)} = 3 \times 10^{-5}T.\]

Vectors kwa kila moja ya michango hii magnetic shamba ni umeonyesha.

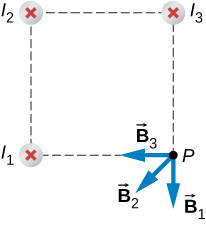
Kielelezo kinaonyesha waya tatu I1, I2, na I3 na sasa inapita ndani ya ukurasa. Wiring huunda pembe tatu za mraba. Sehemu ya magnetic imedhamiriwa kwenye kona ya nne ya mraba ambayo inaitwa P. vector B3 inaongozwa kutoka hatua P kuelekea waya I1. Vector B1 ni kuendelea kwa mstari kutoka kwa waya I3 hadi hatua P. vector B2 iko kati ya vectors B1 na B3.

Sehemu ya magnetic katika mwelekeo wa x ina michango kutoka kwa waya 3 na sehemu ya x ya waya 2:

Template:ContribOpenStaxUni