11.7: Athari ya Hall

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza hali ambapo mashamba magnetic na umeme yanavuka na majeshi yao yanafanana kama chembe ya kushtakiwa inapita kupitia selector kasi.
• Linganisha jinsi flygbolag za malipo zinavyoingia kwenye nyenzo za uendeshaji na kuelezea jinsi hii inahusiana na athari ya Hall

Katika 1879, E.H Hall walipanga majaribio ambayo inaweza kutumika kutambua ishara ya flygbolag malipo predominant katika nyenzo conductive. Kutokana na mtazamo wa kihistoria, jaribio hili lilikuwa la kwanza kuonyesha kwamba flygbolag za malipo katika metali nyingi ni hasi.

Tembelea tovuti hii ili upate maelezo zaidi kuhusu athari za Hall.

Tunachunguza athari ya Hall kwa kusoma mwendo wa elektroni za bure pamoja na mstari wa metali wa upana l katika uwanja wa magnetic wa mara kwa mara (Kielelezo\(\PageIndex{1}\)). Electroni zinahamia kutoka kushoto kwenda kulia, hivyo nguvu ya magnetic wanayopata inawafukuza hadi makali ya chini ya mstari. Hii inacha ziada ya malipo mazuri kwenye makali ya juu ya mstari, na kusababisha uwanja wa umeme E ulioongozwa kutoka juu hadi chini. Mkusanyiko wa malipo kwenye pande zote mbili hujenga mpaka nguvu ya umeme kwenye elektroni katika mwelekeo mmoja ni sawa na nguvu ya magnetic juu yao kwa upande mwingine. Msawazo unafikiwa wakati:

\[eE = ev_d B \label{11.24}\]

ambapo e ni ukubwa wa malipo ya elektroni,\(v_d\) ni kasi ya drift ya elektroni, na E ni ukubwa wa shamba la umeme linaloundwa na malipo yaliyotengwa. Kutatua hili kwa matokeo ya kasi ya drift

\[v_d = \frac{E}{B}. \label{11.25}\]

Kielelezo\(\PageIndex{1}\): Katika athari ya Hall, tofauti tofauti kati ya kando ya juu na chini ya mstari wa chuma huzalishwa wakati wa kusonga flygbolag za malipo zinapigwa na shamba la magnetic. (a) Hall athari kwa flygbolag hasi malipo; (b) Hall athari kwa flygbolag chanya malipo.

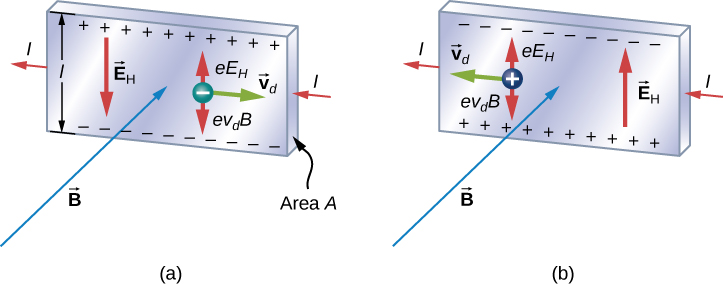
Hali ambapo mashamba ya umeme na magnetic yanapendekezwa kwa kila mmoja inaitwa hali ya shamba la kuvuka. Ikiwa mashamba haya yanazalisha vikosi sawa na kinyume kwenye chembe iliyoshtakiwa na kasi inayofanana na nguvu, chembe hizi zinaweza kupitisha vifaa, vinavyoitwa selector ya kasi, isiyofikiriwa. Kasi hii inawakilishwa katika Equation\ ref {11.26}. Kasi nyingine yoyote ya chembe iliyoshtakiwa iliyotumwa kwenye mashamba sawa ingeondolewa na nguvu ya magnetic au nguvu za umeme.

Kurudi kwenye athari ya Hall, ikiwa sasa katika mstari ni mimi, basi kutoka kwa Sasa na Upinzani, tunajua kwamba

\[I = nev_dA \label{11.26}\]

ambapo n ni idadi ya flygbolag za malipo kwa kiasi na A ni eneo la msalaba wa mstari. Kuchanganya equations kwa\(v_d\) na mimi matokeo katika

\[I = ne\left(\frac{E}{B}\right)A. \label{11.27}\]

Shamba E linahusiana na tofauti tofauti V kati ya kando ya mstari na

\[E = \frac{V}{l}. \label{11.28}\]

Kiasi\(V\) kinachoitwa uwezo wa Hall na inaweza kupimwa kwa voltmeter. Hatimaye, kuchanganya equations kwa mimi na E inatupa

\[V = \dfrac{IBl}{neA} \label{hallV}\]

ambapo makali ya juu ya mstari katika Kielelezo\(\PageIndex{1}\) ni chanya kwa heshima na makali ya chini.

Tunaweza pia kuchanganya Equation\ ref {11.24} na Equation\ ref {11.28} ili kupata usemi kwa voltage ya Hall kwa upande wa shamba la magnetic:

\[V = Blv_d.\]

Nini kama flygbolag malipo ni chanya, kama katika Kielelezo\(\PageIndex{1}\)? Kwa sasa sawa mimi, ukubwa wa V bado unatolewa na Equation\ ref {HallV}. Hata hivyo, makali ya juu sasa ni hasi kwa heshima na makali ya chini. Kwa hiyo, kwa kupima tu ishara ya V, tunaweza kuamua ishara ya flygbolag wengi wa malipo katika chuma.

Hall uwezo vipimo kuonyesha kwamba elektroni ni kubwa malipo flygbolag katika metali nyingi. Hata hivyo, uwezekano wa Hall unaonyesha kuwa kwa metali chache, kama vile tungsten, beryllium, na semiconductors wengi, wengi wa flygbolag za malipo ni chanya. Inageuka kuwa uendeshaji kwa malipo mazuri husababishwa na uhamiaji wa maeneo ya elektroni yanayopotea (inayoitwa mashimo) kwenye ions. Upitishaji kwa mashimo unasomewa baadaye katika Fizikia ya Matter Fizikia.

Athari ya Hall inaweza kutumika kupima mashamba ya magnetic. Ikiwa nyenzo zilizo na wiani unaojulikana wa flygbolag za malipo n zinawekwa kwenye uwanja wa magnetic na V inapimwa, basi shamba linaweza kuamua kutoka kwa Equation\ ref {11.29}. Katika maabara ya utafiti ambapo mashamba ya umeme yanayotumiwa kwa vipimo sahihi yanapaswa kuwa thabiti mno, “probe ya Hall” hutumiwa kwa kawaida kama sehemu ya mzunguko wa umeme unaosimamia shamba.

Mfano\(\PageIndex{1}\): Velocity Selector

Boriti ya elektroni inaingia mchezaji wa kasi ya shamba na mashamba ya magnetic na umeme ya 2.0 mT na\(6.0 \times 10^3 \, N/C\), kwa mtiririko huo. (a) Je, kasi ya boriti ya elektroni inapaswa kupitisha mashamba yaliyovuka yasiyopunguzwa? Ikiwa uwanja wa umeme umezimwa, (b) ni kasi gani ya boriti ya elektroni na (c) ni nini radius ya mwendo wa mviringo unaosababisha?

Mkakati

Boriti ya elektroni haipatikani na mojawapo ya mashamba magnetic au umeme ikiwa majeshi haya yana usawa. Kulingana na majeshi haya ya usawa, tunahesabu kasi ya boriti. Bila uwanja wa umeme, nguvu ya magnetic pekee hutumiwa katika sheria ya pili ya Newton ili kupata kasi. Hatimaye, radius ya njia inategemea mwendo wa mviringo unaosababishwa kutoka kwa nguvu ya magnetic.

Suluhisho

1. Kasi ya boriti isiyoingizwa ya elektroni yenye mashamba yaliyovuka huhesabiwa kwa Equation\ ref {11.25}:\[v_d = \frac{E}{B} = \frac{6 \times 10^3 N/C}{2 \times 10^{-3} T} = 3 \times 10^6 m/s.\]
2. Kuharakisha huhesabiwa kutoka kwa nguvu ya wavu kutoka kwenye uwanja wa magnetic, sawa na kuongeza kasi ya mara nyingi. Ukubwa wa kuongeza kasi ni:\[ma = qvB\]\[a = \frac{qvB}{m} = \frac{(1.6 \times 10^{-19}C)(3 \times 10^6 m/s)(2 \times 10^{-3}T)}{0.1 \times 10^{-31}kg} = 1.1 \times 10^{15} m/s^2.\]
3. Radi ya njia inatokana na usawa wa vikosi vya mviringo na magnetic, au Equation\ ref {11.25}:\[r = \frac{mv}{qB} = \frac{(9.1 \times 10^{-31}kg)(3 \times 10^6 m/s)}{(1.6 \times 10^{-19}C)(2 \times 10^{-3}T)} = 8.5 \times 10^{-3} m.\]

Umuhimu

Ikiwa elektroni katika boriti zilikuwa na kasi juu au chini ya jibu katika sehemu (a), elektroni hizo ingekuwa na nguvu ya wavu yenye nguvu inayotumiwa na uwanja wa magnetic au umeme. Kwa hiyo, elektroni hizo tu katika kasi hii maalum ingeweza kuifanya.

Uwezo wa Hall katika Ribbon ya Fedha

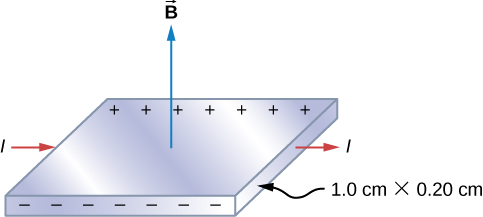
Kielelezo\(\PageIndex{2}\) kinaonyesha Ribbon ya fedha ambayo sehemu ya msalaba ni 1.0 cm na cm 0.20. Ribbon hubeba sasa ya 100 A kutoka kushoto kwenda kulia, na iko katika uwanja sare magnetic ya ukubwa 1.5 T. kutumia thamani wiani wa\(n = 5.9 \times 10^{28}\) elektroni kwa mita za ujazo kwa fedha, kupata uwezo Hall kati ya kingo za Ribbon.

Kielelezo\(\PageIndex{2}\): Kutafuta uwezo wa Hall katika Ribbon ya fedha katika uwanja wa magnetic inavyoonyeshwa.

Mkakati

Kwa kuwa wengi wa flygbolag za malipo ni elektroni, polarity ya voltage ya Hall ni kwamba imeonyeshwa katika takwimu. Thamani ya voltage ya Hall imehesabiwa kwa kutumia Equation\ ref {HallV}.

Suluhisho

Wakati wa kuhesabu voltage ya Hall, tunahitaji kujua sasa kupitia nyenzo, uwanja wa magnetic, urefu, idadi ya flygbolag za malipo, na eneo hilo. Kwa kuwa haya yote yanapewa, voltage ya Hall imehesabiwa kama:

\[\begin{align*} v &= \frac{IBl}{neA} \\[4pt] &= \frac{(100 \, A)(1.5 \, T)(1.0 \times 10^{-2}m)}{(5.9 \times 10^{28} /m^3)(1.6 \times 10^{-19}C)(2.0 \times 10^{-5}m^2)} \\[4pt] &= 7.9 \times 10^{-6}V. \end{align*} \]

Umuhimu

Kama ilivyo katika mfano huu, uwezo wa Hall kwa ujumla ni mdogo sana, na majaribio makini na vifaa nyeti inahitajika kwa kipimo chake.

Zoezi\(\PageIndex{1}\)

Probe ya Hall ina strip ya shaba,\(n = 8.5 \times 10^{28}\) elektroni kwa kila mita ya ujazo, ambayo ni 2.0 cm pana na 0.10 cm nene. Je, ni uwanja wa magnetic wakati mimi = 50 A na uwezo wa Hall ni

1. \(4.0 \, \mu V\)na
2. \(6.0 \, \mu V\)?

Jibu

1.1 T

Jibu b

1.6 T