Skip to main content
Global

11.6: Nguvu na Torque juu ya Loop Sasa

  1. Last updated
  2. Save as PDF
  • Page ID
    176738

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tathmini nguvu ya wavu kwenye kitanzi cha sasa katika uwanja wa nje wa magnetic
    • Tathmini wakati wa wavu kwenye kitanzi cha sasa katika uwanja wa nje wa magnetic
    • Eleza wakati wa magnetic dipole wa kitanzi cha sasa

    Motors ni matumizi ya kawaida ya nguvu ya magnetic kwenye waya za sasa za kubeba. Motors zina vifungo vya waya katika uwanja wa magnetic. Wakati wa sasa unapitia kupitia matanzi, shamba la magnetic lina kasi juu ya matanzi, ambayo huzunguka shimoni. Nishati ya umeme inabadilishwa kuwa kazi ya mitambo katika mchakato. Mara baada ya eneo la uso wa kitanzi limeunganishwa na shamba la magnetic, mwelekeo wa sasa umebadilishwa, kwa hiyo kuna wakati wa kuendelea kwenye kitanzi (Kielelezo\(\PageIndex{1}\)). Ubadilishaji huu wa sasa unafanywa na wasafiri na maburusi. Mtoaji huwekwa ili kurekebisha mtiririko wa sasa kwenye pointi zilizowekwa ili kuweka mwendo wa kuendelea katika magari. Commutator ya msingi ina maeneo matatu ya kuwasiliana ili kuepuka na matangazo yaliyokufa ambapo kitanzi ingekuwa na sifuri instantaneous moment katika hatua hiyo. Vyombo vya habari vya brushes dhidi ya commutator, na kujenga mawasiliano ya umeme kati ya sehemu za commutator wakati wa mwendo unaozunguka.

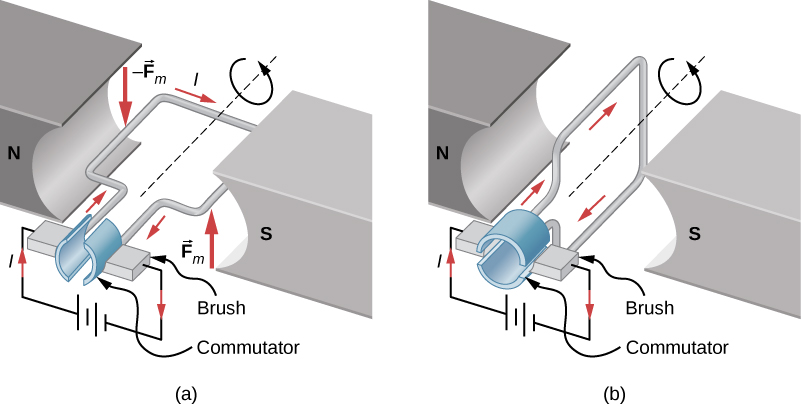
    Mchoro wa motor d c yenye sumaku yenye pengo la usawa, umeme na vichwa vinavyounganishwa na maburusi, waya hupigwa kwenye kitanzi cha mstatili. Mwisho wa waya unaunganishwa na mawasiliano ambayo huunganisha kwenye maburusi ya umeme wakati kitanzi ni cha usawa. Wakati kitanzi ni wima, wao hufanana na pengo kati ya mawasiliano. Ncha ya kaskazini ya sumaku iko upande wa kushoto, pole ya kusini upande wa kulia. Kielelezo a: Kitanzi ni cha usawa na maburusi huwasiliana na kitanzi. Clockwise (kuangalia chini) sasa inapita kupitia kitanzi, hivyo sasa katika sehemu ya kushoto ya kitanzi inapita ndani ya ukurasa, na sasa katika sehemu ya haki inapita nje ya ukurasa. Nguvu ya magnetic kwenye sehemu ya kushoto iko chini, na sehemu ya kulia iko juu. Kitanzi kinazunguka kinyume chake (kuangalia kwenye ukurasa.) Kielelezo b: Kitanzi ni wima. Brushes si katika kuwasiliana na kitanzi. Hakuna mtiririko wa sasa na hakuna nguvu zinazotumiwa.
    Kielelezo\(\PageIndex{1}\): Toleo rahisi la magari ya umeme ya DC. (a) Kitanzi cha waya cha mstatili kinawekwa kwenye uwanja wa magnetic. Majeshi ya waya karibu na miti ya magnetic (N na S) ni kinyume na mwelekeo kama ilivyopangwa na utawala wa kulia-1. Kwa hiyo, kitanzi kina kasi ya wavu na huzunguka kwenye nafasi iliyoonyeshwa katika (b). (b) Brushes sasa kugusa makundi ya commutator ili hakuna sasa inapita kupitia kitanzi. Hakuna wakati unaofanya kitanzi, lakini kitanzi kinaendelea kugeuka kutoka kasi ya awali iliyotolewa kwa sehemu (a). Kwa wakati kitanzi kinapungua, sasa inapita kupitia waya tena lakini sasa kwa upande mwingine, na mchakato unarudia kama sehemu (a). Hii inasababisha mzunguko wa kuendelea wa kitanzi.

    Katika uwanja wa sare ya magnetic, kitanzi cha sasa cha waya, kama kitanzi katika motor, hupata majeshi yote na torques kwenye kitanzi. Kielelezo\(\PageIndex{1}\) kinaonyesha kitanzi cha mstatili cha waya ambacho hubeba sasa mimi na ina pande za urefu a na b. Kitanzi ni katika shamba sare ya magnetic:\(\vec{B} = B\hat{j}\). Nguvu ya magnetic kwenye waya wa moja kwa moja wa sasa wa kubeba urefu l hutolewa na\(I\vec{l} \times \vec{B}\). Ili kupata nguvu wavu juu ya kitanzi, tuna kutumia equation hii kwa kila moja ya pande nne. Nguvu upande wa 1 ni

    \[\vec{F}_1 = IaB \sin(90^o - \theta) \hat{i} = IaB \cos\theta \hat{i}\]

    ambapo mwelekeo umeamua na RHR-1. Ya sasa katika upande wa 3 inapita katika mwelekeo kinyume na ule wa upande wa 1, hivyo

    \[\vec{F}_3 = -IaB \sin(90^o + \theta)\hat{i} = -IaB \cos \theta \hat{i}\]

    Maji katika pande 2 na 4 ni perpendicular\(\vec{B}\) na nguvu za pande hizi ni

    \[\vec{F}_2 = IbB\hat{k}\]

    \[\vec{F}_4 = -IbB\hat{k}.\]

    Sasa tunaweza kupata nguvu ya wavu kwenye kitanzi:

    \[\sum \vec{F}_{net} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \vec{F}_4 = 0.\]

    Ingawa matokeo haya\((\sum F = 0)\) yamepatikana kwa kitanzi cha mstatili, ni mbali zaidi na inashikilia loops za sasa za kubeba maumbo ya kiholela; yaani, hakuna nguvu ya wavu kwenye kitanzi cha sasa katika shamba la sare la magnetic.

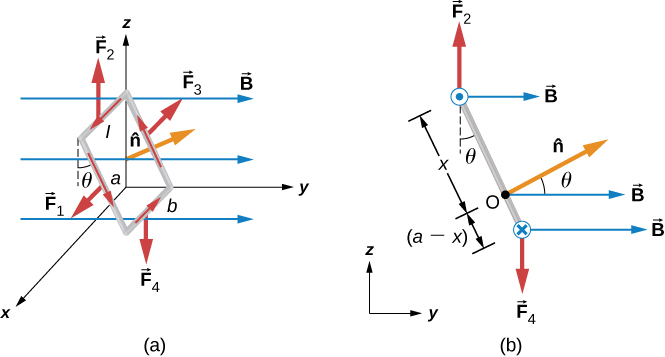
    Mfano wa kitanzi mstatili kubeba sasa I. sasa katika kitanzi ni kinyume chake wakati kutazamwa kutoka chanya y mwelekeo kuangalia kuelekea asili. Kitanzi ni katika shamba sare ya magnetic, B, ambayo inaelezea haki. Kielelezo a inaonyesha mtazamo wa mwelekeo wa 3 wa kitanzi. Pande za juu na za chini ni sawa na mhimili x na zina urefu b. upande wa juu ni saa y = 0 na z chanya na sasa katika mwelekeo chanya x. Upande wa chini ni katika y nzuri na z=0 na ina sasa katika mwelekeo hasi x. Pande mbili zilizobaki zina urefu b. moja ni katika x = 0 na ina sasa kwenda juu, na moja ni katika x chanya na ina sasa kwenda juu. Pande hizi zinaelekezwa kwenye theta ya angle juu kwa heshima na mhimili wa z. Mwelekeo wa vector kitengo katika kawaida kwa eneo la kitanzi mstatili inavyoonyeshwa. Majeshi ya kila pande pia yanaonyeshwa. F 1 ni nguvu kwenye upande uliojitokeza kwenye x nzuri, na inaonyesha katika mwelekeo mzuri wa x. F 2 ni nguvu upande wa juu na inaonyesha juu. F 3 ni nguvu kwenye upande uliojitokeza kwenye x=0 na pointi katika mwelekeo hasi x. F 4 ni nguvu juu ya chini na pointi chini. Kielelezo b kinaonyesha mtazamo wa upande wa kitanzi, ili tuweze kuangalia ndege ya y z na kuona tu upande uliojitokeza, ambayo hufanya angle ya theta na wima juu. Ya sasa inatoka kwetu juu ya kitanzi, na sasa inaingia kwenye ukurasa chini. Nguvu F 2 juu ni juu, nguvu F 4 chini ni chini. n kofia vector pointi juu na kulia, kwa pembe ya theta kwa shamba B. egemeo uhakika O ambayo sisi ni kuhesabu moment inavyoonekana umbali x kutoka juu ya kitanzi, na -x kutoka chini.
    Kielelezo\(\PageIndex{2}\): (a) Kitanzi cha sasa cha mstatili katika shamba la sare la magnetic kinakabiliwa na wakati wa wavu lakini si nguvu ya wavu. (b) Mtazamo wa upande wa coil.

    Ili kupata wakati wa wavu kwenye kitanzi cha sasa kilichoonyeshwa kwenye Kielelezo\(\PageIndex{2a}\), tunazingatia kwanza\(F_1\) na\(F_3\). Kwa kuwa wana mstari huo wa hatua na ni sawa na kinyume, jumla ya torques yao kuhusu mhimili wowote ni sifuri (tazama Mzunguko wa Axis Fast-Axis). Kwa hiyo, ikiwa kuna wakati wowote juu ya kitanzi, lazima iwe na samani\(F_2\) na\(F_4\). Hebu tuhesabu torques karibu na mhimili unaopita kupitia hatua O ya Kielelezo\(\PageIndex{2b}\) (mtazamo wa upande wa coil) na ni perpendicular kwa ndege ya ukurasa. Hatua O ni umbali x kutoka upande wa 2 na umbali\((a - x)\) kutoka upande wa 4 wa kitanzi. wakati silaha ya\(F_2\)\(x \, sin \, \theta\) na\(F_4\) ni\((a - x)\space sin \, \theta\), kwa mtiririko huo, hivyo moment wavu juu ya kitanzi ni

    \[\sum \vec{\tau} = \vec{\tau}_1 + \vec{\tau}_2 + \vec{\tau}_3 + \vec{\tau}_4 = F_2 x \, sin \, \theta \hat{i} - F_4 (a - x) \, sin \, (\theta) \hat{i}\]\[- IbBx \, sin \, \theta \hat{i} - IbB(a - x) sin \, \theta \hat{i}.\]

    Hii inaeleza\[\vec{\tau} = - IAB \, sin \, \theta \hat{i}\] mahali ambapo\(A = ab\) ni eneo la kitanzi.

    Kumbuka kwamba wakati huu ni huru ya x; kwa hiyo ni huru ya mahali ambapo O iko katika ndege ya kitanzi cha sasa. Kwa hiyo, kitanzi hupata wakati huo huo kutoka kwenye uwanja wa magnetic kuhusu mhimili wowote katika ndege ya kitanzi na sambamba na x -axis.

    Kitanzi kilichofungwa-sasa kinajulikana kama dipole ya magnetic na neno IA linajulikana kama wakati wake wa magnetic dipole\(\mu\). Kweli, wakati wa magnetic dipole ni vector inayofafanuliwa kama

    \[\vec{\mu} = IA \hat{n}\]wapi\(\hat{n}\) vector kitengo kilichoelekezwa perpendicular kwa ndege ya kitanzi (angalia Mchoro\(\PageIndex{2}\)). Mwelekeo wa\(\hat{n}\) hupatikana kwa RHR-2—ikiwa unapunguza vidole vya mkono wako wa kulia katika mwelekeo wa mtiririko wa sasa katika kitanzi, basi alama yako ya kidole kando\(\hat{n}\). Ikiwa kitanzi kina N zamu za waya, basi wakati wake wa magnetic dipole hutolewa na

    \[\vec{\mu} = NIA\hat{n}.\]

    Kwa upande wa wakati wa magnetic dipole, wakati wa kitanzi cha sasa kutokana na shamba sare ya magnetic inaweza kuandikwa tu kama

    \[\vec{\tau} = \vec{\mu} \times \vec{B}.\]

    Equation hii inashikilia kitanzi cha sasa katika ndege mbili-dimensional ya sura ya kiholela.

    Kutumia hesabu inayofanana na ile iliyopatikana katika Capacitance kwa dipole ya umeme, nishati ya uwezo wa dipole ya magnetic ni

    \[U = -\vec{\mu} \cdot \vec{B}.\]

    Mfano\(\PageIndex{1}\): Forces and Torques on Current-Carrying Loops

    Kitanzi cha sasa cha mviringo cha radius 2.0 cm hubeba sasa ya 2.0 mA. (a) Ukubwa wa wakati wake wa magnetic dipole ni nini? (b) Ikiwa dipole inaelekezwa kwa digrii 30 kwenye uwanja wa sare wa magnetic wa ukubwa wa 0.50 T, ni ukubwa gani wa wakati unaopata na ni nguvu gani?

    Mkakati

    Wakati wa dipole hufafanuliwa na nyakati za sasa eneo la kitanzi. Eneo la kitanzi linaweza kuhesabiwa kutoka eneo la mduara. Wakati juu ya kitanzi na uwezo wa nishati huhesabiwa kutoka kutambua wakati wa magnetic, shamba la magnetic, na angle iliyoelekezwa kwenye shamba.

    Suluhisho

    1. Wakati wa magnetic μ huhesabiwa kwa nyakati za sasa eneo la kitanzi au\(\pi r^2\). \[\mu = IA = (2.0 \times 10^{-3} A)(\pi (0.02 \, m)^2) = 2.5 \times 10^{-6} A \cdot m^2\]
    2. Nishati na uwezo wa nishati huhesabiwa kwa kutambua wakati wa magnetic, shamba la magnetic, na angle kati ya vectors hizi mbili. Mahesabu ya kiasi hiki ni:\[\tau = \vec{\mu} \times \vec{B} = \mu B \, sin \, \theta = (2.5 \times 10^{-6} A \cdot m^2)(0.50 T) sin(30^o) = 6.3 \times 10^{-7}N \cdot m\]\[U = -\vec{\mu} \cdot \vec{B} = - \mu B cos \theta = - (2.5 \times 10^{-6} A \cdot m^2)(0.50 T) cos (30^o) = -1.1 \times 10^{-6}J.\]

    Umuhimu

    Dhana ya wakati wa magnetic katika ngazi ya atomiki inajadiliwa katika sura inayofuata. Dhana ya kuunganisha wakati wa magnetic na shamba la magnetic ni utendaji wa vifaa kama motors magnetic, ambapo kubadili shamba la nje la magnetic husababisha mzunguko wa mara kwa mara wa kitanzi kama anajaribu kuunganisha na shamba ili kupunguza nishati yake ya uwezo.

    Zoezi\(\PageIndex{1}\)

    Katika mwelekeo gani ingekuwa dipole ya magnetic inapaswa kuzalisha (a) kasi ya juu katika uwanja wa magnetic? (b) Nishati ya juu ya dipole?

    Suluhisho

    a. iliyokaa au kupambana na iliyokaa; b. perpendicular

    Wachangiaji na Majina

    Template:ContribOpenStaxUni