9.4: Resistivity na Upinzani

Last updated
Save as PDF

Page ID: 176194

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Tofauti kati ya upinzani na resistivity
Eleza conductivity mrefu
Eleza sehemu ya umeme inayojulikana kama kupinga
Weka uhusiano kati ya upinzani wa kupinga na urefu wake, eneo la msalaba, na resistivity
Hali ya uhusiano kati ya resistivity na joto

Ni nini kinachoendesha sasa? Tunaweza kufikiria vifaa mbalimbali-kama vile betri, jenereta, maduka ya ukuta, na kadhalika-ambazo ni muhimu kudumisha sasa. Vifaa vyote vile huunda tofauti tofauti na hujulikana kama vyanzo vya voltage. Wakati chanzo cha voltage kinaunganishwa na kondakta, inatumika tofauti tofauti V ambayo inajenga uwanja wa umeme. Shamba la umeme, kwa upande wake, lina nguvu kwa mashtaka ya bure, na kusababisha sasa. Kiasi cha sasa kinategemea si tu juu ya ukubwa wa voltage, lakini pia juu ya sifa za nyenzo ambazo sasa zinapita. Vifaa vinaweza kupinga mtiririko wa mashtaka, na kipimo cha kiasi gani nyenzo kinapinga mtiririko wa mashtaka hujulikana kama resistivity. Resistivity hii ni sawa na msuguano kati ya vifaa viwili vinavyopinga mwendo.

Resistivity

Wakati voltage inatumiwa kwa conductor, shamba la umeme\(\vec{E}\) linaundwa, na mashtaka katika conductor huhisi nguvu kutokana na uwanja wa umeme. Uzito wa sasa\(\vec{J}\) ambao matokeo hutegemea uwanja wa umeme na mali ya vifaa. Utegemezi huu unaweza kuwa ngumu sana. Katika vifaa vingine, ikiwa ni pamoja na metali kwenye joto lililopewa, wiani wa sasa ni takriban sawia na uwanja wa umeme. Katika kesi hizi, wiani wa sasa unaweza kuonyeshwa kama

\[\vec{J} = \sigma \vec{E},\]

wapi\(\sigma\) conductivity umeme. Conductivity ya umeme ni sawa na conductivity ya mafuta na ni kipimo cha uwezo wa vifaa vya kufanya au kusambaza umeme. Wafanyakazi wana conductivity ya juu ya umeme kuliko wahamiaji. Tangu conductivity umeme ni\(\sigma = J/E\), vitengo ni

\[\sigma = \dfrac{|J|}{|E|} = \dfrac{A/m^2}{V/m} = \dfrac{A}{V \cdot m}.\]

Hapa, tunafafanua kitengo kinachoitwa ohm na alama ya Kigiriki kubwa omega,\(\Omega\). Kitengo hicho kinaitwa jina la Georg Simon Ohm, ambaye tutajadili baadaye katika sura hii. The\(\Omega\) ni kutumika ili kuepuka machafuko na idadi 0. Ohm moja ni sawa na volt moja kwa amp:\(1 \, \Omega = 1 \, V/A\). Kwa hiyo vitengo vya conductivity umeme ni hivyo\((\Omega \cdot m)^{-1}\).

Conductivity ni mali ya ndani ya nyenzo. Mali nyingine ya ndani ya nyenzo ni resistivity, au resistivity umeme. Resistivity ya nyenzo ni kipimo cha jinsi nguvu nyenzo inapinga mtiririko wa sasa umeme. Ishara ya resistivity ni barua ya chini ya Kigiriki rho,\(\rho\), na resistivity ni usawa wa conductivity umeme:

\[\rho = \dfrac{1}{\sigma}.\]

Kitengo cha resistivity katika vitengo SI ni ohm-mita\((\Omega \cdot m\). Tunaweza kufafanua resistivity kwa suala la uwanja wa umeme na wiani wa sasa.

\[\rho = \dfrac{E}{J}.\]

Zaidi ya resistivity, shamba kubwa inahitajika kuzalisha wiani wa sasa. Chini ya resistivity, wiani mkubwa wa sasa unaozalishwa na shamba la umeme lililopewa. Waendeshaji wazuri wana conductivity ya juu na resistivity ya chini. Wahamiaji nzuri wana conductivity ya chini na resistivity ya juu. \(\PageIndex{1}\)Orodha ya meza resistivity na maadili conductivity kwa vifaa mbalimbali.

Vifaa vilivyoorodheshwa kwenye meza vinatenganishwa katika makundi ya wasimamizi, semiconductors, na wahamiaji, kulingana na makundi mapana ya resistivity. Wafanyabiashara wana resistivity ndogo zaidi, na wahamiaji wana kubwa zaidi; semiconductors wana resistivity kati. Wafanyabiashara wana densiti tofauti lakini kubwa, bila malipo, ilhali mashtaka mengi katika vihami yanafungwa na atomi na hawana huru kuhamia. Semiconductors ni kati, kuwa na mashtaka machache ya bure kuliko waendeshaji, lakini kuwa na mali zinazofanya idadi ya mashtaka ya bure hutegemea sana aina na kiasi cha uchafu katika semiconductor. Mali hizi za kipekee za semiconductors zinatumiwa katika umeme wa kisasa, kama tutakavyochunguza katika sura za baadaye.

Mfano\(\PageIndex{1}\): Current Density, Resistance, and Electrical field for a Current-Carrying Wire

Tumia wiani wa sasa, upinzani, na uwanja wa umeme wa urefu wa 5 m wa waya wa shaba na kipenyo cha 2.053 mm (12-geji) inayobeba sasa ya\(I - 10 \, mA\).

Mkakati

Tunaweza kuhesabu wiani wa sasa kwa kutafuta kwanza eneo la msalaba wa waya, yaani\(A = 3.31 \, mm^2\), na ufafanuzi wa wiani wa sasa\(J = \dfrac{I}{A}\). Upinzani unaweza kupatikana kwa kutumia urefu wa waya\(L = 5.00 \, m\), eneo, na resistivity ya shaba\(\rho = 1.68 \times 10^{-8} \Omega \cdot m\), wapi\(R = \rho \dfrac{L}{A}\). Resistivity na wiani wa sasa inaweza kutumika kupata uwanja wa umeme.

Suluhisho

Kwanza, tunahesabu wiani wa sasa:

\[\begin {align*} J &= \dfrac{I}{A} \\[5pt] &= \dfrac{10 \times 10^{-3} A}{3.31 \times 10^{-6} m^2} \\[5pt] &= 3.02 \times 10^3 \dfrac{A}{m^2}. \end{align*}\]

Upinzani wa waya ni

\[\begin {align*}R &= \rho \dfrac{L}{A} \\[5pt] &= (1.68 \times 10^{-8} \Omega \cdot m) \dfrac{5.00 \, m}{3.31 \times 10^{-6}m^2} \\[5pt] &= 0.025 \, \Omega.\end{align*}\]

Hatimaye, tunaweza kupata uwanja wa umeme:

\[\begin {align*}E &= \rho J \\[5pt] &= 1.68 \times 10^{-8} \Omega \cdot m \left(3.02 \times 10^3 \dfrac{A}{m^2}\right) \\[5pt] &= 5.07 \times 10^{-5} \dfrac{V}{m}.\end{align*}\]

Umuhimu

Kutoka kwa matokeo haya, haishangazi kwamba shaba hutumiwa kwa waya kwa kubeba sasa kwa sababu upinzani ni mdogo sana. Kumbuka kuwa wiani wa sasa na uwanja wa umeme ni huru na urefu wa waya, lakini voltage inategemea urefu.

Zoezi\(\PageIndex{1}\)

Wiring wa shaba hutumia mara kwa mara kwa kamba za ugani na wiring wa nyumba kwa sababu kadhaa. Copper ina kiwango cha juu cha conductivity ya umeme, na kwa hiyo kiwango cha chini cha resistivity, cha metali zote zisizo na thamani. Pia muhimu ni nguvu ya kukimbia, ambapo nguvu ya kukimbia ni kipimo cha nguvu inayotakiwa kuvuta kitu hadi mahali ambapo huvunja. Nguvu ya kukimbia ya nyenzo ni kiwango cha juu cha shida ya kukimbia ambayo inaweza kuchukua kabla ya kuvunja. Copper ina high tensile nguvu,\(2 \times 10^8 \, \dfrac{N}{m^2}\). Tabia ya tatu muhimu ni ductility. Ductility ni kipimo cha uwezo wa vifaa vya kupatikana ndani ya waya na kipimo cha kubadilika kwa nyenzo, na shaba ina ductility ya juu. Kuhitimisha, kwa conductor kuwa mgombea mzuri kwa ajili ya kufanya waya, kuna angalau sifa tatu muhimu: resistivity chini, high tensile nguvu, na high ductility. Nini vifaa vingine vinavyotumiwa kwa wiring na ni faida gani na hasara?

Jibu: Fedha, dhahabu, na alumini zote hutumiwa kufanya waya. Vifaa vyote vinne vina conductivity ya juu, fedha yenye juu zaidi. Zote nne zinaweza kupatikana kwa urahisi ndani ya waya na kuwa na nguvu kubwa ya kukimbia, ingawa sio juu kama shaba. Hasara dhahiri ya dhahabu na fedha ni gharama, lakini waya za fedha na dhahabu hutumiwa kwa matumizi maalum, kama vile waya za msemaji. Dhahabu haina oxidize, na kufanya uhusiano bora kati ya vipengele. Wiring za alumini zina vikwazo vyao. Aluminium ina resistivity ya juu kuliko shaba, hivyo kipenyo kikubwa kinahitajika ili kufanana na upinzani kwa urefu wa waya za shaba, lakini alumini ni nafuu kuliko shaba, hivyo hii sio drawback kubwa. Waya wa alumini hawana nguvu ya juu ya ductility na nguvu kama shaba, lakini nguvu ya ductility na tensile ni ndani ya viwango vya kukubalika. Kuna wasiwasi machache ambayo yanapaswa kushughulikiwa katika kutumia alumini na huduma lazima itumike wakati wa kufanya uhusiano. Aluminium ina kiwango cha juu cha upanuzi wa mafuta kuliko shaba, ambayo inaweza kusababisha uhusiano huru na hatari ya moto iwezekanavyo. Oxidation ya alumini haifanyi na inaweza kusababisha matatizo. Mbinu maalum zinapaswa kutumika wakati wa kutumia waya za alumini na vipengele, kama vile maduka ya umeme, lazima ziundwa kukubali waya za alumini.

Phet

Tazama simulation hii ya maingiliano ili kuona madhara ya eneo la msalaba, urefu, na resistivity ya waya ni juu ya upinzani wa conductor. Kurekebisha vigezo kwa kutumia slide baa na kuona kama upinzani inakuwa ndogo au kubwa.

Joto Utegemezi wa Resistivity

Kuangalia nyuma kwenye Jedwali\(\PageIndex{1}\), utaona safu iliyoitwa “Mgawo wa Joto.” Resistivity ya vifaa vingine ina utegemezi mkubwa wa joto. Katika vifaa vingine, kama vile shaba, resistivity huongezeka kwa joto la kuongezeka. Kwa kweli, katika metali nyingi za kufanya, resistivity huongezeka kwa joto la kuongezeka. Joto la kuongezeka husababisha kuongezeka kwa vibrations ya atomi katika muundo wa kimiani wa metali, ambayo huzuia mwendo wa elektroni. Katika vifaa vingine, kama vile kaboni, resistivity hupungua kwa joto la kuongezeka. Katika vifaa vingi, utegemezi ni takriban linear na unaweza kutajwa kwa kutumia equation linear:

\[\rho \approx \rho_0 [1 + \alpha (T - T_0)],\]

wapi\(\rho\) resistivity ya nyenzo katika joto T,\(\alpha\) ni mgawo wa joto wa nyenzo, na\(\rho_0\) ni resistivity katika\(T_0\), kawaida kuchukuliwa kama\(T_0 = 20.00^oC\).

Kumbuka pia kwamba mgawo wa joto\(\alpha\) ni hasi kwa semiconductors waliotajwa katika Jedwali\(\PageIndex{1}\), maana yake ni kwamba resistivity yao inapungua kwa joto la kuongezeka. Wao huwa conductors bora katika joto la juu, kwa sababu kuongezeka kwa uchochezi wa mafuta huongeza idadi ya mashtaka ya bure inapatikana kubeba sasa. Mali hii ya kupungua\(\rho\) kwa joto pia inahusiana na aina na kiasi cha uchafu uliopo katika semiconductors.

Upinzani

Sasa tunazingatia upinzani wa waya au sehemu. Upinzani ni kipimo cha jinsi vigumu kupitisha sasa kupitia waya au sehemu. Upinzani unategemea resistivity. Resistivity ni tabia ya nyenzo zinazotumiwa kutengeneza waya au sehemu nyingine ya umeme, wakati upinzani ni tabia ya waya au sehemu.

Ili kuhesabu upinzani, fikiria sehemu ya kufanya waya na eneo la msalaba A, urefu L, na resistivity\(\rho\). Betri imeunganishwa kwenye kondakta, kutoa tofauti tofauti\(\Delta V\) katika hiyo (Kielelezo\(\PageIndex{1}\)). Tofauti ya uwezo hutoa shamba la umeme linalofanana na wiani wa sasa, kulingana na\(\vec{E} = \rho \vec{J}\).

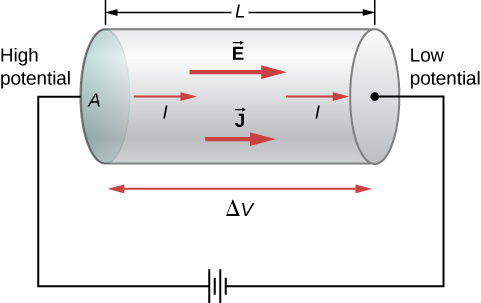
Picha ni kuchora schematic ya betri iliyounganishwa na kondakta na eneo la msalaba A. mtiririko wa sasa kutoka upande wa juu wa uwezo hadi upande wa chini wa uwezo wa kondakta. — Kielelezo\(\PageIndex{1}\): Uwezo unaotolewa na betri unatumika kwa sehemu ya conductor na eneo la msalaba\(A\) na urefu\(L\).

Ukubwa wa uwanja wa umeme katika sehemu ya kondakta ni sawa na voltage iliyogawanywa na urefu\(E = V/L\), na ukubwa wa wiani wa sasa ni sawa na sasa umegawanyika na eneo la msalaba,\(J = I/A\). Kutumia habari hii na kukumbuka kuwa uwanja wa umeme ni sawia na resistivity na wiani wa sasa, tunaweza kuona kwamba voltage ni sawia na sasa:

\[\begin{align*} E &= \rho J \\[4pt] \dfrac{V}{L} &= \rho \dfrac{I}{A} \\[4pt] V &= \left(\rho \dfrac{L}{A}\right) I. \end{align*}\]

Ufafanuzi: Upinzani

Uwiano wa voltage hadi sasa hufafanuliwa kama upinzani\(R\):

\[R \equiv \dfrac{V}{I}.\]

Upinzani wa sehemu ya cylindrical ya conductor ni sawa na resistivity ya nyakati nyenzo urefu umegawanyika na eneo:

\[R \equiv \dfrac{V}{I} = \rho \dfrac{L}{A}.\]

Kitengo cha upinzani ni ohm,\(\Omega\). Kwa voltage iliyotolewa, juu ya upinzani, chini ya sasa.

Vipinga

Sehemu ya kawaida katika nyaya za elektroniki ni kupinga. Kupinga inaweza kutumika kupunguza mtiririko wa sasa au kutoa tone la voltage. Kielelezo\(\PageIndex{2}\) inaonyesha alama kutumika kwa ajili ya kupinga katika michoro schematic ya mzunguko. Viwango viwili vinavyotumiwa kwa michoro za mzunguko hutolewa na Taasisi ya Taifa ya Taifa ya Marekani (ANSI, inayojulikana “an-kuona”) na Tume ya Kimataifa ya Electrotechnical (IEC). Mifumo yote hutumiwa kwa kawaida. Tunatumia kiwango cha ANSI katika maandishi haya kwa utambuzi wake wa kuona, lakini tunaona kuwa kwa nyaya kubwa, ngumu zaidi, kiwango cha IEC kinaweza kuwa na uwasilishaji safi, na iwe rahisi kusoma.

Kielelezo A inaonyesha alama ya ANSI kwa kupinga. Kielelezo B kinaonyesha ishara ya IEC ya kupinga. — Kielelezo\(\PageIndex{2}\): Alama kwa kupinga kutumika katika michoro mzunguko. (a) Ishara ya ANSI; (b) ishara ya IEC.

Utegemezi wa nyenzo na sura ya upinzani

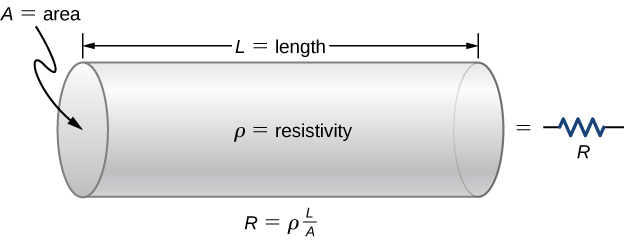
Kupinga inaweza kuonyeshwa kama silinda yenye eneo la msalaba A na urefu L, uliofanywa kwa nyenzo na resistivity\(\rho\) (Kielelezo\(\PageIndex{3}\)). Upinzani wa kupinga ni\(R = \rho \dfrac{L}{A}\)

Picha ni kuchora schematic ya kupinga. Ni silinda sare ya urefu L na eneo la msalaba A. — Kielelezo\(\PageIndex{3}\): Mfano wa kupinga kama silinda sare ya urefu L na eneo la msalaba A. Upinzani wake kwa mtiririko wa sasa ni sawa na upinzani unaofanywa na bomba kwa mtiririko wa maji. Kwa muda mrefu silinda, upinzani wake mkubwa. Sehemu kubwa ya msalaba A, ndogo ya upinzani wake.

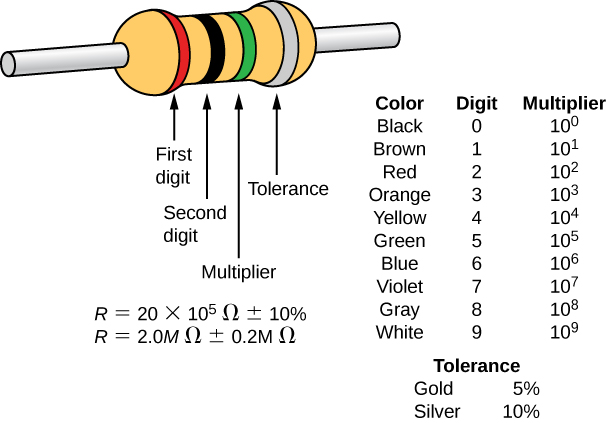
Nyenzo za kawaida zinazotumiwa kufanya kupinga ni kaboni. Njia ya kaboni imefungwa karibu na msingi wa kauri, na vichwa viwili vya shaba vinaunganishwa. Aina ya pili ya kupinga ni kupinga filamu ya chuma, ambayo pia ina msingi wa kauri. Njia hiyo inafanywa kutoka kwa vifaa vya oksidi ya chuma, ambayo ina mali ya semiconductive sawa na kaboni. Tena, vichwa vya shaba vinaingizwa kwenye mwisho wa kupinga. Kupinga ni kisha rangi na alama kwa ajili ya kitambulisho. Kupinga ina bendi nne za rangi, kama inavyoonekana kwenye Kielelezo\(\PageIndex{4}\).

Picha ni kuchora schematic ya kupinga. Ina bendi nne za rangi: nyekundu, nyeusi, kijani, na kijivu. — Kielelezo\(\PageIndex{4}\): Vipinga vingi vinafanana na takwimu iliyoonyeshwa hapo juu. Bendi nne hutumiwa kutambua kupinga. Bendi mbili za kwanza za rangi zinawakilisha tarakimu mbili za kwanza za upinzani wa kupinga. Rangi ya tatu ni multiplier. Rangi ya nne inawakilisha uvumilivu wa kupinga. Resistor inavyoonekana ina upinzani wa\(20 \times 10^5 \, \Omega \pm 10\%\)

Upinzani mbalimbali juu ya maagizo mengi ya ukubwa. Baadhi ya vihami vya kauri, kama vile wale waliotumiwa kusaidia mistari ya nguvu, wana upinzani wa\(10^{12} \, \Omega\) au zaidi. Mtu kavu anaweza kuwa na upinzani wa mkono hadi mguu wa\(10^5 \, \Omega\) wakati upinzani wa moyo wa mwanadamu ni juu Kipande\(10^3 \, \Omega\) cha mita cha waya kubwa ya shaba inaweza kuwa na upinzani wa\(10^{-5} \, \Omega\), na superconductors hawana upinzani wakati wote katika joto la chini. Kama tulivyoona, upinzani unahusiana na sura ya kitu na nyenzo ambazo zinajumuisha.

Upinzani wa kitu pia hutegemea joto, kwani\(R_0\) ni sawa sawa na\(\rho\). Kwa silinda, tunajua\(R = \rho \dfrac{L}{A}\), hivyo kama L na A hazibadilika sana na joto, R ina utegemezi sawa wa joto kama\(\rho\). (Uchunguzi wa coefficients ya upanuzi wa mstari unaonyesha kuwa amri mbili za ukubwa chini ya coefficients ya kawaida ya joto ya resistivity, hivyo athari za joto kwenye L na A ni kuhusu amri mbili za ukubwa chini ya juu\(\rho\).) Hivyo,

\[R = R_0(1 + \alpha \Delta T) \label{Tdep}\]

ni utegemezi wa joto wa upinzani wa kitu, wapi\(R_0\) upinzani wa awali (kawaida huchukuliwa kuwa\(T = 20.00^oC\) na R ni upinzani baada ya mabadiliko ya joto\(\Delta T\). Msimbo wa rangi hutoa upinzani wa kupinga kwa joto la\(T = 20.00^oC\).

Thermometers nyingi zinategemea athari za joto juu ya upinzani (Kielelezo\(\PageIndex{5}\)). Moja ya thermometers ya kawaida inategemea thermistor, kioo cha semiconductor na utegemezi mkubwa wa joto, upinzani ambao hupimwa kupata joto lake. Kifaa ni chache, ili iwe haraka katika usawa wa joto na sehemu ya mtu inayogusa.

Picha ni picha ya thermometers mbili za mdomo. — Kielelezo\(\PageIndex{5}\): Thermometers hizi za kawaida zinategemea kipimo cha automatiska cha upinzani wa joto la thermistor.

Mfano\(\PageIndex{2}\): Calculating Resistance

Ingawa tahadhari lazima itumike katika kutumia\(\rho = \rho_0 (1 + \alpha \Delta T)\) na\(R = R_0(1 + \alpha \Delta T)\) kwa mabadiliko ya joto zaidi kuliko\(100^oC\), kwa tungsten, equations hufanya kazi vizuri kwa mabadiliko makubwa ya joto. Filament ya tungsten katika\(20^oC\) ina upinzani wa\(0.350 \, \Omega\). Je, upinzani ungekuwa nini ikiwa joto linaongezeka hadi\(2850^oC\)?

Mkakati

Hii ni matumizi ya moja kwa moja ya Equation\ ref {Tdep}, kwani upinzani wa awali wa filament hutolewa kama\(R_0 = 0.350 \, \Omega\) na mabadiliko ya joto ni\(\Delta T = 2830^oC\).

Suluhisho

Upinzani wa filament ya moto\(R\) hupatikana kwa kuingia maadili inayojulikana katika equation hapo juu:

\[\begin{align*} R &= R_0(1 + \alpha \Delta T) \\[5pt] &= (0.350 \, \Omega)\left(1 + \left(\dfrac{4.5 \times 10^{-3}}{^oC}\right)(2830^oC)\right) \\[5pt] &= 4.8 \, \Omega \end{align*} \]

Umuhimu

Kumbuka kwamba upinzani hubadilika kwa zaidi ya sababu ya 10 kama filament inapunguza joto la juu na sasa kupitia filament inategemea upinzani wa filament na voltage kutumika. Ikiwa filament hutumiwa katika bomba la mwanga wa incandescent, sasa ya awali kupitia filament wakati bulb ni ya kwanza yenye nguvu itakuwa kubwa zaidi kuliko sasa baada ya filament kufikia joto la uendeshaji.

Zoezi\(\PageIndex{2}\)

Upimaji wa matatizo ni kifaa cha umeme kupima matatizo, kama inavyoonyeshwa hapo chini. Inajumuisha msaada rahisi, kuhami ambao unasaidia muundo wa foil conduction. Upinzani wa foil hubadilika kama msaada umewekwa. Je, upinzani wa kupima matatizo hubadilikaje? Je, kipimo cha matatizo kinaathiriwa na mabadiliko ya joto?

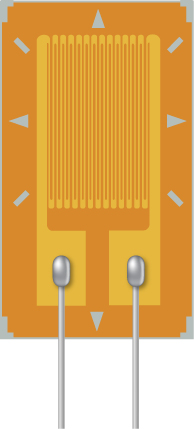
Picha ni kuchora kwa schematic ya kifaa cha kupima matatizo ambayo ina muundo wa uendeshaji uliowekwa kwenye uso wa maboksi. Mawasiliano ya chuma hufanywa kwa usafi mbili kubwa kwa asili ya muundo wa kuendesha

Jibu: Mfano wa foil unasimama kama kuunga mkono kunenea, na nyimbo za foil zinakuwa za muda mrefu na nyembamba. Tangu upinzani ni mahesabu kama\(R = \rho \dfrac{L}{A}\), the resistance increases as the foil tracks are stretched. When the temperature changes, so does the resistivity of the foil tracks, changing the resistance. One way to combat this is to use two strain gauges, one used as a reference and the other used to measure the strain. The two strain gauges are kept at a constant temperature

The Resistance of Coaxial Cable

Long cables can sometimes act like antennas, picking up electronic noise, which are signals from other equipment and appliances. Coaxial cables are used for many applications that require this noise to be eliminated. For example, they can be found in the home in cable TV connections or other audiovisual connections. Coaxial cables consist of an inner conductor of radius \(r_i\) surrounded by a second, outer concentric conductor with radius \(r_0\) (Figure \(\PageIndex{6}\)). The space between the two is normally filled with an insulator such as polyethylene plastic. A small amount of radial leakage current occurs between the two conductors. Determine the resistance of a coaxial cable of length L.

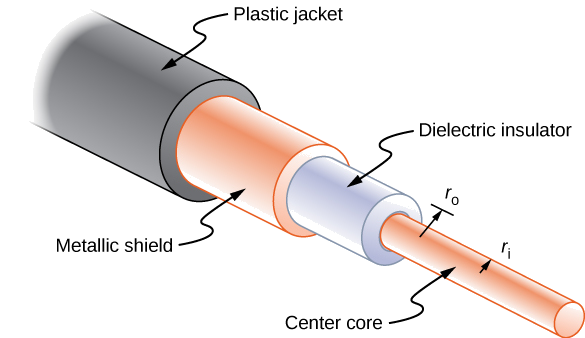
Picture is a schematic drawing of a coaxial cable. It consists of a central metal core encapsulated by the dielectric insulator. Metal shield surrounds dielectric insulator. The whole assembly in inserted in the plastic jacket. — Figure \(\PageIndex{6}\): Coaxial cables consist of two concentric conductors separated by insulation. They are often used in cable TV or other audiovisual connections.

Strategy

We cannot use the equation \(R = \rho \dfrac{L}{A}\) directly. Instead, we look at concentric cylindrical shells, with thickness dr, and integrate.

Solution

We first find an expression for \(dR\) and then integrate from \(r_i\) to \(r_0\),

\[\begin{align*} dR &= \dfrac{\rho}{A} dr \\[5pt] &= \dfrac{\rho}{2 \pi r L} dr, \end{align*}\]

Integrating both sides

\[\begin{align*} R &= \int_{r_i}^{r_0} dR \\[5pt] &= \int_{r_i}^{r_0} \dfrac{\rho}{2 \pi r L} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \int_{r_i}^{r_0} \dfrac{1}{r} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \ln \dfrac{r_0}{r_i}.\end{align*}\]

Significance

The resistance of a coaxial cable depends on its length, the inner and outer radii, and the resistivity of the material separating the two conductors. Since this resistance is not infinite, a small leakage current occurs between the two conductors. This leakage current leads to the attenuation (or weakening) of the signal being sent through the cable.

Exercise \(\PageIndex{3}\)

The resistance between the two conductors of a coaxial cable depends on the resistivity of the material separating the two conductors, the length of the cable and the inner and outer radius of the two conductor. If you are designing a coaxial cable, how does the resistance between the two conductors depend on these variables?

Answer: The longer the length, the smaller the resistance. The greater the resistivity, the higher the resistance. The larger the difference between the outer radius and the inner radius, that is, the greater the ratio between the two, the greater the resistance. If you are attempting to maximize the resistance, the choice of the values for these variables will depend on the application. For example, if the cable must be flexible, the choice of materials may be limited.

Phet: Battery-Resistor Circuit

View this simulation to see how the voltage applied and the resistance of the material the current flows through affects the current through the material. You can visualize the collisions of the electrons and the atoms of the material effect the temperature of the material.

Material	Uendeshaji,\(\sigma\)\((\Omega \cdot m)^{-1}\)	Resistivity,\(\rho\)\((\Omega \cdot m)\)	Mgawo wa joto\(\alpha\)\((^oC)^{-1}\)
Makondakta
Fedha	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(6.29 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(1.59 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0038
Copper	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(5.95 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(1.68 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0039
Dhahabu	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(4.10 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(2.44 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0034
Aluminium	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(3.77 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(2.65 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0039
Tungsten	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(1.79 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(5.60 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0045
Iron	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(1.03 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(9.71 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0065
Platinamu	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.94 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10.60 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0039
Steel	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.50 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(20.00 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Kiongozi	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.45 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(22.00 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Manganin (Cu, Mn. Ni alloy)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.21 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(48.20 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.000002
Constantan (Cu, Ni alloy)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.20 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(49.00 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.00003
Mercury	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.10 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(98.00 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0009
Nichrome (Ni, Fe, Cr alloy)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(0.10 \times 10^7\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(100.00 \times 10^{-8}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.0004
Semiconductors [1]
Carbon (safi)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(2.86 \times 10^{4}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(3.50 \times 10^{-5}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.0005
Carbon	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\((2.86 - 1.67) \times 10^{-6}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\((3.5 - 60) \times 10^{-5}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.0005
Germanium (safi)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(600 \times 10^{-3}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.048
Germanium	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\((1 - 600) \times 10^{-3}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.050
Silicon (safi)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 2300	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.075
Silicon	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> 0.1 - 2300	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402"> -0.07
Vihami
Kaharabu	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(2.00 \times 10^{-15}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(5 \times 10^{14}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Kioo	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{-9} - 19^{-14}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^9 - 10^{14}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Lucite	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(< 10^{-13}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(> 10^{13}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Mica	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{-11} - 10^{-15}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{11} - 10^{15}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Quartz (fused)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(1.33 \times 10^{-18}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(75 \times 10^{16}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Mpira (ngumu)	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{-13} - 10^{-16}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{13} - 10^{16}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Sulfuri	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{-15}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{15}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Teflon ^TM	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(< 10^{-13}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(> 10^{13}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">
Wood	\ (\ sigma\)\((\Omega \cdot m)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^{-8} - 10^{-11}\)	\ (\ rho\)\((\Omega \cdot m)\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">\(10^8 - 10^{11}\)	\ (\ alpha\)\((^oC)^{-1}\) Makondakta semiconductors [1] Vihami” class="lt-phys-4402">