9.3: Mfano wa uendeshaji katika Vyuma
- Page ID
- 176261
Mwishoni mwa sehemu hii, utaweza:
- Kufafanua kasi drift ya mashtaka ya kusonga kwa njia ya chuma
- Eleza wiani wa sasa wa vector
- Eleza uendeshaji wa taa ya incandescent
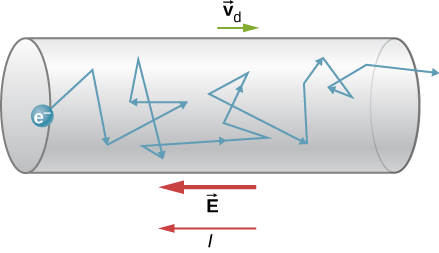
Wakati elektroni zinakwenda kupitia waya wa uendeshaji, hazihamia kwa kasi ya mara kwa mara, yaani, elektroni hazihamia kwenye mstari wa moja kwa moja kwa kasi ya mara kwa mara. Badala yake, wanaingiliana na kugongana na atomi na elektroni nyingine za bure katika kondakta. Kwa hiyo, elektroni huhamia kwa mtindo wa zig-zag na hupitia kupitia waya. Tunapaswa pia kutambua kwamba ingawa ni rahisi kujadili mwelekeo wa sasa, sasa ni kiasi cha scalar. Wakati wa kujadili kasi ya mashtaka kwa sasa, ni sahihi zaidi kujadili wiani wa sasa. Tutarudi kwenye wazo hili mwishoni mwa sehemu hii.
drift kasi
Ishara za umeme zinahamia haraka sana. Mazungumzo ya simu yaliyofanywa na mikondo katika waya hufunika umbali mkubwa bila ucheleweshaji unaoonekana Taa zinakuja haraka kama kubadili mwanga kunahamishwa kwenye nafasi ya 'juu'. Ishara nyingi za umeme zinazotolewa na mikondo husafiri kwa kasi\(10^8 m/s\) kwa utaratibu wa sehemu kubwa ya kasi ya mwanga. Kushangaza, mashtaka ya mtu binafsi kwamba kufanya juu ya hoja ya sasa polepole sana kwa wastani, kawaida drifting kwa kasi juu ya utaratibu wa\(10^{-4}m/s\). Tunawezaje kupatanisha kasi hizi mbili, na inatuambia nini kuhusu wasimamizi wa kawaida?
Kasi ya ishara ya umeme inatokana na ukweli kwamba nguvu kati ya mashtaka hufanya haraka kwa mbali. Hivyo, wakati malipo ya bure yanalazimika kwenye waya, kama ilivyo kwenye Kielelezo\(\PageIndex{1}\), malipo yanayoingia inasubu mashtaka mengine mbele yake kutokana na nguvu ya kupuuza kati ya mashtaka kama hayo. Mashtaka haya ya kusonga kusonga kushinikiza mashtaka zaidi chini ya mstari. Uzito wa malipo katika mfumo hauwezi kuongezeka kwa urahisi, hivyo ishara inapitishwa haraka. Wimbi la mshtuko wa umeme linakwenda kupitia mfumo kwa karibu kasi ya mwanga. Ili kuwa sahihi, ishara hii ya kusonga kwa haraka, au wimbi la mshtuko, ni mabadiliko ya kueneza haraka katika uwanja wa umeme.
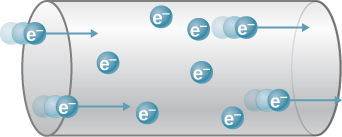
Good conductors have large numbers of free charges. In metals, the free charges are free electrons. (In fact, good electrical conductors are often good heat conductors too, because large numbers of free electrons can transport thermal energy as well as carry electrical current.) Figure \(\PageIndex{2}\) shows how free electrons move through an ordinary conductor. The distance that an individual electron can move between collisions with atoms or other electrons is quite small. The electron paths thus appear nearly random, like the motion of atoms in a gas. But there is an electrical field in the conductor that causes the electrons to drift in the direction shown (opposite to the field, since they are negative). The drift velocity \(\vec{v}_d\) is the average velocity of the free charges. Drift velocity is quite small, since there are so many free charges. If we have an estimate of the density of free electrons in a conductor, we can calculate the drift velocity for a given current. The larger the density, the lower the velocity required for a given current.
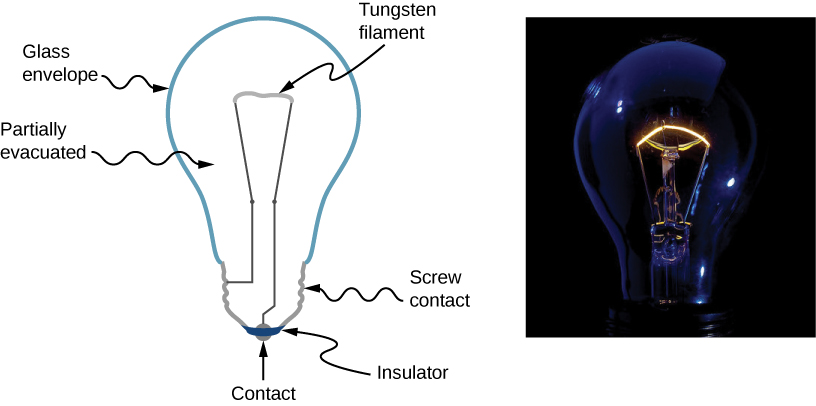
Free-electron collisions transfer energy to the atoms of the conductor. The electrical field does work in moving the electrons through a distance, but that work does not increase the kinetic energy (nor speed) of the electrons. The work is transferred to the conductor’s atoms, often increasing temperature. Thus, a continuous power input is required to keep a current flowing. (An exception is superconductors, for reasons we shall explore in a later chapter. Superconductors can have a steady current without a continual supply of energy—a great energy savings.) For a conductor that is not a superconductor, the supply of energy can be useful, as in an incandescent light bulb filament (Figure \(\PageIndex{3}\)). The supply of energy is necessary to increase the temperature of the tungsten filament, so that the filament glows.
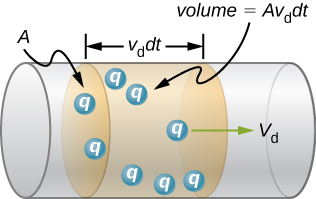
We can obtain an expression for the relationship between current and drift velocity by considering the number of free charges in a segment of wire, as illustrated in Figure \(\PageIndex{4}\). The number of free charges per unit volume, or the number density of free charges, is given the symbol \(n\) where
\[n = \dfrac{\text{number of charges}}{\text{volume}}.\]
The value of \(n\) depends on the material. The shaded segment has a volume \(Av_d \, dt\), so that the number of free charges in the volume is \(nAv_d \, dt\). The charge \(dQ\) in this segment is thus \(qnAv_d \, dt\), where \(q\) is the amount of charge on each carrier. (The magnitude of the charge of electrons is \(q = 1.60 \times 10^{-19} \, C\).) Current is charge moved per unit time; thus, if all the original charges move out of this segment in time dt, the current is
\[I = \dfrac{dQ}{dt} = qn Av_d.\]
Rearranging terms gives
\[v_d = \dfrac{I}{nqA}\]
where
- \(v_d\) is the drift velocity,
- \(n\) is the free charge density,
- \(A\) is the cross-sectional area of the wire, and
- \(I\) is the current through the wire.
The carriers of the current each have charge q and move with a drift velocity of magnitude \(v_d\).
Note that simple drift velocity is not the entire story. The speed of an electron is sometimes much greater than its drift velocity. In addition, not all of the electrons in a conductor can move freely, and those that do move might move somewhat faster or slower than the drift velocity. So what do we mean by free electrons?
Atoms in a metallic conductor are packed in the form of a lattice structure. Some electrons are far enough away from the atomic nuclei that they do not experience the attraction of the nuclei as strongly as the inner electrons do. These are the free electrons. They are not bound to a single atom but can instead move freely among the atoms in a “sea” of electrons. When an electrical field is applied, these free electrons respond by accelerating. As they move, they collide with the atoms in the lattice and with other electrons, generating thermal energy, and the conductor gets warmer. In an insulator, the organization of the atoms and the structure do not allow for such free electrons.
As you know, electric power is usually supplied to equipment and appliances through round wires made of a conducting material (copper, aluminum, silver, or gold) that are stranded or solid. The diameter of the wire determines the current-carrying capacity—the larger the diameter, the greater the current-carrying capacity. Even though the current-carrying capacity is determined by the diameter, wire is not normally characterized by the diameter directly. Instead, wire is commonly sold in a unit known as “gauge.” Wires are manufactured by passing the material through circular forms called “drawing dies.” In order to make thinner wires, manufacturers draw the wires through multiple dies of successively thinner diameter. Historically, the gauge of the wire was related to the number of drawing processes required to manufacture the wire. For this reason, the larger the gauge, the smaller the diameter. In the United States, the American Wire Gauge (AWG) was developed to standardize the system. Household wiring commonly consists of 10-gauge (2.588-mm diameter) to 14-gauge (1.628-mm diameter) wire. A device used to measure the gauge of wire is shown in Figure \(\PageIndex{5}\).

Calculate the drift velocity of electrons in a copper wire with a diameter of 2.053 mm (12-gauge) carrying a 20.0-A current, given that there is one free electron per copper atom. (Household wiring often contains 12-gauge copper wire, and the maximum current allowed in such wire is usually 20.0 A.) The density of copper is \(8.80 \times 10^3 kg/m^3 \) and the atomic mass of copper is 63.54 g/mol.
Strategy
We can calculate the drift velocity using the equation \(I = nqAv_d\). The current is \(I = 20.00 \, A\) and \(q = 1.60 \times 10{-19}C\) is the charge of an electron. We can calculate the area of a cross-section of the wire using the formula \(A = \pi r^2\), where \(r\) is one-half the diameter. The given diameter is 2.053 mm, so r is 1.0265 mm. We are given the density of copper, \(8.80 \times 10^3 kg/m^3\), and the atomic mass of copper is \(63.54 \, g/mol\). We can use these two quantities along with Avogadro’s number, \(6.02 \times 10^{23} \, atoms/mol\), to determine n, the number of free electrons per cubic meter.
Solution
First, we calculate the density of free electrons in copper. There is one free electron per copper atom. Therefore, the number of free electrons is the same as the number of copper atoms per \(m^3\). We can now find n as follows:
\[\begin{align*} n &= \dfrac{1 \, e^-}{atom} \times \dfrac{6.02 \times 10^{23} atoms}{mol} \times \dfrac{1 \, mol}{63.54 \, g} \times \dfrac{1000 \, g}{kg} \times \dfrac{8.80 \times 10^3kg}{1 \, m^3} \\[5pt] &= 8.34 \times 10^{28} e^- /m^3. \end{align*}\]
The cross-sectional area of the wire is
\[\begin{align*} A &= \pi r^2 \\[5pt] &= \pi \left(\dfrac{2.05 \times 10^{-3}m}{2} \right)^2 \\[5pt] &= 3.30 \times 10^{-6}m^2. \end{align*}\]
Rearranging \(I = nqAv_d\) to isolate drift velocity gives
\[\begin{align*} v_d &= \dfrac{I}{nqA} \\[5pt] &= \dfrac{20.00 \, A}{(8.34 \times 10^{28}/m^3)(-1.60 \times 10^{-19}C)(3.30 \times 10^{-6}m^2)} \\[5pt] &= -4.54 \times 10^{-4} m/s. \end{align*}\]
Significance
The minus sign indicates that the negative charges are moving in the direction opposite to conventional current. The small value for drift velocity (on the order of \(10^{-4} m/s\) confirms that the signal moves on the order of \(10^{12}\) times faster (about \(10^8 m/s\) than the charges that carry it.
In Example \(\PageIndex{1}\), the drift velocity was calculated for a 2.053-mm diameter (12-gauge) copper wire carrying a 20-amp current. Would the drift velocity change for a 1.628-mm diameter (14-gauge) wire carrying the same 20-amp current?
- Answer
-
The diameter of the 14-gauge wire is smaller than the diameter of the 12-gauge wire. Since the drift velocity is inversely proportional to the cross-sectional area, the drift velocity in the 14-gauge wire is larger than the drift velocity in the 12-gauge wire carrying the same current. The number of electrons per cubic meter will remain constant.
Current Density
Although it is often convenient to attach a negative or positive sign to indicate the overall direction of motion of the charges, current is a scalar quantity, \(I = \dfrac{dQ}{dt}.\) It is often necessary to discuss the details of the motion of the charge, instead of discussing the overall motion of the charges. In such cases, it is necessary to discuss the current density, \(\vec{J}\), a vector quantity. The current density is the flow of charge through an infinitesimal area, divided by the area. The current density must take into account the local magnitude and direction of the charge flow, which varies from point to point. The unit of current density is ampere per meter squared, and the direction is defined as the direction of net flow of positive charges through the area.
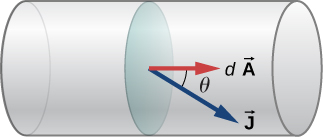
The relationship between the current and the current density can be seen in Figure\(\PageIndex{6}\). The differential current flow through the area \(d\vec{A}\) is found as
\[dI = \vec{J} \cdot d\vec{A} = J dA \, \cos \, \theta,\]
where \(\theta\) is the angle between the area and the current density. The total current passing through area \(d\vec{A}\) can be found by integrating over the area,
\[I = \iint_{area} \vec{J} \cdot d\vec{A}.\]
Consider the magnitude of the current density, which is the current divided by the area:
\[J = \dfrac{I}{A} = \dfrac{n|q| Av_d}{A} = n |q|v_d.\]
Thus, the current density is \(\vec{J} = nq\vec{v}_d\). If q is positive, \(\vec{v}_d\) is in the same direction as the electrical field \(\vec{E}\). If q is negative, \(\vec{v}_d\) is in the opposite direction of \(\vec{E}\). Either way, the direction of the current density \(\vec{J}\) is in the direction of the electrical field \(\vec{E}\).
The current supplied to a lamp with a 100-W light bulb is 0.87 amps. The lamp is wired using a copper wire with diameter 2.588 mm (10-gauge). Find the magnitude of the current density.
Strategy
The current density is the current moving through an infinitesimal cross-sectional area divided by the area. We can calculate the magnitude of the current density using \(J = \dfrac{I}{A}\). The current is given as 0.87 A. The cross-sectional area can be calculated to be \(A = 5.26 \, mm^2\).
Solution
Calculate the current density using the given current \(I = 0.87 \, A\) and the area, found to be \(A = 5.26 \, mm^2\).
\[J = \dfrac{I}{A} = \dfrac{0.87 \, A}{5.26 \times 10^{-6} m^2} = 1.65 \times 10^5 \dfrac{A}{m^2}.\]
Significance
The current density in a conducting wire depends on the current through the conducting wire and the cross-sectional area of the wire. For a given current, as the diameter of the wire increases, the charge density decreases.
The current density is proportional to the current and inversely proportional to the area. If the current density in a conducting wire increases, what would happen to the drift velocity of the charges in the wire?
- Answer
-
The current density in a conducting wire increases due to an increase in current. The drift velocity is inversely proportional to the current \(\left( v_d = \dfrac{nqA}{I}\right)\), so the drift velocity would decrease.
What is the significance of the current density? The current density is proportional to the current, and the current is the number of charges that pass through a cross-sectional area per second. The charges move through the conductor, accelerated by the electric force provided by the electrical field. The electrical field is created when a voltage is applied across the conductor. In Ohm’s Law, we will use this relationship between the current density and the electrical field to examine the relationship between the current through a conductor and the voltage applied.


