7.4: Mahesabu ya Uwezo wa Umeme

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tumia uwezo kutokana na malipo ya uhakika
• Tumia uwezo wa mfumo wa mashtaka mengi ya uhakika
• Eleza dipole ya umeme
• Eleza wakati wa dipole
• Tumia uwezekano wa usambazaji wa malipo ya kuendelea

Madai ya uhakika, kama vile elektroni, ni miongoni mwa vitalu vya msingi vya jengo. Zaidi ya hayo, mgawanyo wa malipo ya spherical (kama vile malipo kwenye nyanja ya chuma) huunda mashamba ya nje ya umeme hasa kama malipo ya uhakika. Uwezo wa umeme kutokana na malipo ya uhakika ni, kwa hiyo, kesi tunayohitaji kuzingatia.

Tunaweza kutumia calculus kupata kazi zinazohitajika kuhamisha malipo ya mtihani q kutoka umbali mkubwa mbali na umbali wa r kutoka malipo ya uhakika q. Kuzingatia uhusiano kati ya kazi na uwezo\(W = -q\Delta V\), kama katika sehemu ya mwisho, tunaweza kupata matokeo yafuatayo.

Uwezo wa umeme\(V\) of a Point Charge

Uwezo\(V\) wa umeme wa malipo ya uhakika hutolewa na

\[\underbrace{V = \dfrac{kq}{r}}_{\text{point charge}} \label{PointCharge}\]

ambapo\(k\) ni mara kwa mara sawa na\(9.0 \times 10^9 \, N \cdot m^2/C^2\).

Uwezo katika Equation\ ref {PointCharge} katika infinity huchaguliwa kuwa sifuri. Kwa hiyo,\(V\) kwa malipo ya uhakika hupungua kwa umbali, wakati\(\vec{E}\) kwa malipo ya uhakika hupungua kwa umbali wa mraba:

\[E = \dfrac{F}{q_t} = \dfrac{kq}{r^2}\]

Kumbuka kwamba uwezo wa umeme V ni scalar na hauna mwelekeo, wakati uwanja wa umeme\(\vec{E}\) ni vector. Ili kupata voltage kutokana na mchanganyiko wa mashtaka ya uhakika, unaongeza voltages ya mtu binafsi kama namba. Ili kupata uwanja wa jumla wa umeme, lazima uongeze mashamba ya mtu binafsi kama vectors, kuchukua ukubwa na mwelekeo katika akaunti. Hii ni sawa na ukweli kwamba V inahusishwa kwa karibu na nishati, scalar, ambapo\(\vec{E}\) inahusishwa kwa karibu na nguvu, vector.

Mfano\(\PageIndex{1}\): What Voltage Is Produced by a Small Charge on a Metal Sphere?

Mashtaka katika umeme tuli ni kawaida katika nanocoulomb (NC) kwa microcoulomb\((\mu C)\) mbalimbali. Je, ni voltage 5.00 cm mbali na katikati ya nyanja ya chuma imara ya 1-cm-kipenyo ambayo ina malipo ya tuli ya -3.00-NC?

Mkakati

Kama tulivyojadiliwa katika Mashtaka ya Umeme na Mashamba, malipo kwenye nyanja ya chuma huenea kwa usawa na hutoa shamba kama ile ya malipo ya uhakika iko katikati yake. Hivyo, tunaweza kupata voltage kwa kutumia equation\(V = \dfrac{kq}{r}\).

Suluhisho

Kuingia maadili inayojulikana katika usemi kwa uwezekano wa malipo ya uhakika (Equation\ ref {PointCharge}), tunapata

\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (9.00 \times 10^9 \, N \cdot m^2/C^2)\left(\dfrac{-3.00 \times 10^{-9}C}{5.00 \times 10^{-2}m}\right) \nonumber \\[4pt] &= - 539 \, V. \nonumber \end{align} \nonumber \]

Umuhimu

Thamani hasi ya voltage inamaanisha malipo mazuri yatavutiwa kutoka umbali mkubwa, kwani uwezo ni wa chini (hasi zaidi) kuliko umbali mkubwa. Kinyume chake, malipo mabaya yangeondolewa, kama inavyotarajiwa.

Mfano\(\PageIndex{2}\): What Is the Excess Charge on a Van de Graaff Generator?

Jenereta ya Van de Graaff ya maandamano ina nyanja ya chuma ya kipenyo cha 25.0 cm ambayo inazalisha voltage ya kV 100 karibu na uso wake (Kielelezo). Ni malipo gani ya ziada yanayokaa kwenye nyanja? (Kudhani kwamba kila thamani ya namba hapa inavyoonekana na takwimu tatu muhimu.)

Kielelezo\(\PageIndex{1}\): Voltage ya jenereta hii ya maandamano Van de Graaff inapimwa kati ya nyanja ya kushtakiwa na ardhi. Uwezo wa dunia unachukuliwa kuwa sifuri kama kumbukumbu. Uwezo wa nyanja ya kushtakiwa ya kushtakiwa ni sawa na ile ya malipo sawa ya uhakika katikati yake.

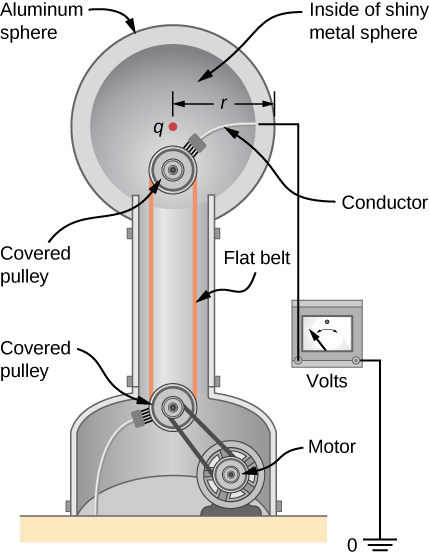
Mkakati

Uwezo juu ya uso ni sawa na ule wa malipo ya uhakika katikati ya nyanja, umbali wa cm 12.5. (Radi ya nyanja ni 12.5 cm.) Tunaweza hivyo kuamua malipo ya ziada kwa kutumia Equation\ ref {PointCharge}

\[V = \dfrac{kq}{r}.\]

Suluhisho

Kutatua\(q\) na kuingia maadili inayojulikana hutoa

\[\begin{align} q &= \dfrac{rV}{k} \nonumber \\[4pt] &= \dfrac{(0.125 \, m)(100 \times 10^3 \, V)}{8.99 \times 10^9 N \cdot m^2/C^2} \nonumber \\[4pt] &= 1.39 \times 10^{-6} C \nonumber \\[4pt] &= 1.39 \, \mu C. \nonumber \end{align} \nonumber \]

Umuhimu

Hii ni malipo madogo, lakini hutoa voltage kubwa sana. Tuna dalili nyingine hapa kwamba ni vigumu kuhifadhi mashtaka ya pekee.

Zoezi\(\PageIndex{1}\)

Je, ni uwezo gani ndani ya nyanja ya chuma katika Mfano\(\PageIndex{1}\)?

Suluhisho

\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (8.99 \times 10^9 N \cdot m^2/C^2) \left(\dfrac{-3.00 \times 10^{-9} C}{5.00 \times 10^{-3} m}\right) \nonumber \\[4pt] &= - 5390 \, V\nonumber \end{align} \nonumber \]

Kumbuka kwamba shamba la umeme ndani ya conductor ni sifuri. Kwa hiyo, njia yoyote kutoka hatua juu ya uso hadi hatua yoyote katika mambo ya ndani itakuwa na integrand ya sifuri wakati wa kuhesabu mabadiliko katika uwezo, na hivyo uwezo katika mambo ya ndani ya nyanja ni sawa na ile juu ya uso.

Vikwazo katika mifano hii miwili inaweza kupimwa na mita ambayo inalinganisha uwezo wa kipimo na uwezo wa ardhi. Uwezo wa chini mara nyingi huchukuliwa kuwa sifuri (badala ya kuchukua uwezo katika infinity kuwa sifuri). Ni tofauti ya uwezo kati ya pointi mbili ambazo ni za umuhimu, na mara nyingi sana kuna dhana ya kimyakimya kwamba hatua fulani ya kumbukumbu, kama vile Dunia au hatua ya mbali sana, iko kwenye uwezo wa sifuri. Kama ilivyoelezwa hapo awali, hii ni sawa na kuchukua kiwango cha bahari kama\(h = 0\) wakati wa kuzingatia nishati ya uwezo wa mvuto\(U_g = mgh\).

Mifumo ya Malipo mengi ya Point

Kama vile uwanja wa umeme unatii kanuni ya superposition, ndivyo uwezo wa umeme. Fikiria mfumo unao na mashtaka ya N\(q_1,q_2,. . ., q_N\). Je, ni uwezo wa umeme wa V katika hatua ya nafasi P kutoka kwa mashtaka haya? Kila moja ya mashtaka haya ni malipo ya chanzo ambayo hutoa uwezo wake wa umeme katika hatua P, bila kujitegemea mabadiliko mengine yoyote yanaweza kufanya. Hebu\(V_1, V_2, . . ., V_N\) uwezekano wa umeme katika P zinazozalishwa na mashtaka\(q_1,q_2,. . ., q_N\), kwa mtiririko huo. Kisha, uwezo wa umeme wa wavu\(V_p\) katika hatua hiyo ni sawa na jumla ya uwezo wa umeme wa mtu binafsi. Unaweza kuonyesha kwa urahisi hili kwa kuhesabu nishati ya uwezo wa malipo ya mtihani unapoleta malipo ya mtihani kutoka kwenye hatua ya kumbukumbu kwenye infinity hadi kumweka P:

\[V_p = V_1 + V_2 + . . . + V_N = \sum_1^N V_i.\]

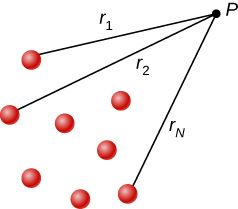
Kumbuka kuwa uwezo wa umeme hufuata kanuni sawa ya superposition kama uwanja wa umeme na nishati ya uwezo wa umeme. Ili kuonyesha hili kwa uwazi zaidi, kumbuka kuwa malipo ya mtihani kwenye\(q_i\) hatua P katika nafasi ina umbali wa\(r_1,r_2, . . . ,r_N\) kutoka kwa mashtaka ya N yaliyowekwa katika nafasi hapo juu, kama inavyoonekana kwenye Kielelezo\(\PageIndex{2}\). Kutumia formula yetu kwa uwezekano wa malipo ya uhakika kwa kila moja ya haya (kudhani kuwa uhakika) mashtaka, tunaona kwamba

\[V_p = \sum_1^N k\dfrac{q_i}{r_i} = k\sum_1^N \dfrac{q_i}{r_i}. \label{eq20}\]

Kwa hiyo, uwezo wa umeme wa malipo ya mtihani ni

\[U_p = q_tV_p = q_tk\sum_1^N \dfrac{q_i}{r_i},\]ambayo ni sawa na kazi ya kuleta malipo ya mtihani ndani ya mfumo, kama inavyoonekana katika sehemu ya kwanza ya sura.

Kielelezo\(\PageIndex{2}\): Uthibitisho wa umbali wa moja kwa moja kutoka kwa mashtaka hadi hatua ya nafasi P.

Dipole ya Umeme

Dipole ya umeme ni mfumo wa mashtaka mawili sawa lakini kinyume umbali fasta mbali. Mfumo huu hutumika kutengeneza mifumo mingi ya ulimwengu halisi, ikiwa ni pamoja na mwingiliano wa atomiki na Masi. Moja ya mifumo hii ni molekuli ya maji, chini ya hali fulani. Hali hizi hukutana ndani ya tanuri ya microwave, ambapo mashamba ya umeme na maelekezo mbadala hufanya molekuli za maji zibadilishe mwelekeo. Vibration hii ni sawa na joto katika ngazi ya Masi.

Mfano\(\PageIndex{3}\): Electric Potential of a Dipole

Fikiria dipole katika Kielelezo\(\PageIndex{3}\) na ukubwa wa malipo ya\(q = 3.0 \, \mu C\) na umbali wa kujitenga Ni uwezo\(d = 4.0 \, cm.\) gani katika maeneo yafuatayo katika nafasi? (a) (0, 0, 1.0 cm); (b) (0, 0, -5.0 cm); (c) (3.0 cm, 0, 2.0 cm).

Kielelezo\(\PageIndex{3}\): Mchoro wa jumla wa dipole ya umeme, na alama ya umbali kutoka kwa mashtaka ya mtu binafsi hadi hatua P katika nafasi.

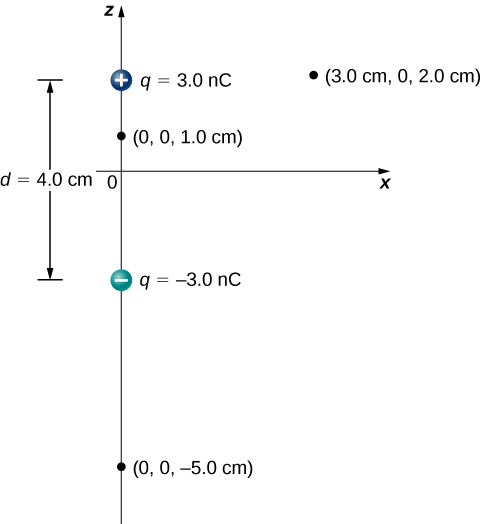
Mkakati

Omba\(V_p = k \sum_1^N \dfrac{q_i}{r_i}\) kwa kila moja ya pointi hizi tatu.

Suluhisho

a.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.010 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = 1.8 \times 10^3 \, V\)

b.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.070 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = -5.1 \times 10^2 \, V\)

c.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.030 \, m} - \dfrac{3.0\space nC}{0.050 \, m}\right) = 3.6 \times 10^2 \, V\)

Umuhimu

Kumbuka kuwa kutathmini uwezo ni rahisi zaidi kuliko uwanja wa umeme, kutokana na uwezekano wa kuwa scalar badala ya vector.

Zoezi\(\PageIndex{1}\)

Je, ni uwezo gani juu ya x -axis? Z -axis

Suluhisho

Uwezo wa x -axis ni sifuri, kwa sababu ya mashtaka sawa na kinyume umbali sawa kutoka kwao. On z -axis, tunaweza superimpose uwezo mbili; tutaona kwamba kwa\(z > > d\), tena uwezo huenda sifuri kutokana na kufuta.

Sasa hebu tuangalie kesi maalum wakati umbali wa uhakika P kutoka kwa dipole ni mkubwa zaidi kuliko umbali kati ya mashtaka katika dipole,\(r >> d\); kwa mfano, wakati sisi ni nia ya uwezo wa umeme kutokana na molekuli polarized kama vile molekuli ya maji. Hii sio mbali (infinity) kwamba tunaweza tu kutibu uwezo kama sifuri, lakini umbali ni mkubwa wa kutosha kwamba tunaweza kurahisisha mahesabu yetu kuhusiana na mfano uliopita.

Tunaanza kwa kubainisha kuwa katika\(\PageIndex{4}\) Kielelezo uwezo hutolewa na

\[V_p = V_+ + V_- = k \left( \dfrac{q}{r_+} - \dfrac{q}{r_-} \right)\]

wapi

\[r_{\pm} = \sqrt{x^2 + \left(z \pm \dfrac{d}{2}\right)^2}.\]

Kielelezo\(\PageIndex{4}\): Mchoro wa jumla wa dipole ya umeme, na alama ya umbali kutoka kwa mashtaka ya mtu binafsi hadi hatua P katika nafasi.

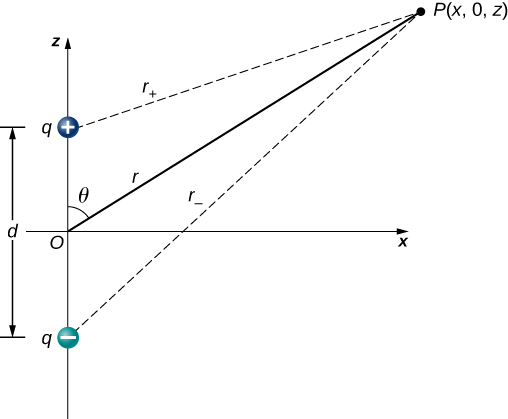
Hii bado ni formula halisi. Ili kuchukua faida ya ukweli kwamba\(r \gg d\), tunaandika upya radii kwa suala la kuratibu polar,\(x = r \, \sin \, \theta\) na z = r\,\ cos\,\ theta\). Hii inatupa

\[r_{\pm} = \sqrt{r^2 \, \sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}.\]

Tunaweza kurahisisha maneno haya kwa kuunganisha r nje ya mizizi,

\[r_{\pm} = \sqrt{\sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}\]

na kisha kuzidisha mabano

\[r_{\pm} = r \sqrt{\sin^2\space \theta + \cos^2 \, \theta \pm \cos \, \theta\dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2}.\]

Muda wa mwisho katika mizizi ni ndogo ya kutosha kuwa duni (kumbuka\(r >> d\), na hivyo\((d/r)^2\) ni ndogo sana, kwa ufanisi sifuri kwa kiwango ambacho tutaweza kupima), na kutuacha

\[r_{\pm} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r}}.\]

Kwa kutumia makadirio binomial (matokeo ya kiwango kutoka hisabati ya mfululizo, wakati\(a\) ni ndogo)

\[\dfrac{1}{\sqrt{1 \pm a}} \approx 1 \pm \dfrac{a}{2}\]

na kubadilisha hii katika formula yetu kwa\(V_p\), sisi kupata

\[V_p = k\left[\dfrac{q}{r}\left(1 + \dfrac{d \, \cos \, \theta}{2r} \right) - \dfrac{q}{r}\left(1 - \dfrac{d \, \cos \, \theta}{2r}\right)\right] = k\dfrac{qd \, \cos \theta}{r^2}.\]

Hii inaweza kuandikwa kwa urahisi zaidi ikiwa tunafafanua kiasi kipya, wakati wa umeme wa dipole,

\[\vec{p} = q\vec{d},\]

ambapo wadudu hawa wanasema kutoka hasi kwa malipo mazuri. Kumbuka kuwa hii ina ukubwa qd. Kiasi hiki kinatuwezesha kuandika uwezo katika hatua P kutokana na dipole katika asili kama

\[V_p = k\dfrac{\vec{p} \cdot \hat{r}}{r^2}.\]

Mchoro wa matumizi ya formula hii umeonyeshwa kwenye Kielelezo\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\): Jiometri kwa ajili ya matumizi ya uwezo wa dipole.

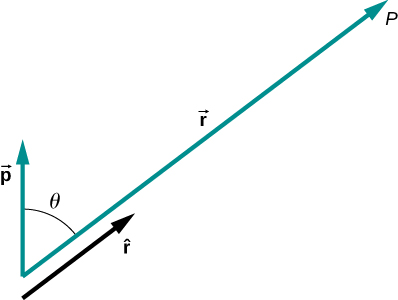
Pia kuna wakati wa juu zaidi, kwa quadrupoles, octupoles, na kadhalika. Utaona haya katika madarasa ya baadaye.

Uwezo wa Mgawanyiko wa malipo ya kuendelea

Tumekuwa tukifanya kazi na mashtaka ya uhakika sana, lakini vipi kuhusu mgawanyo wa malipo ya kuendelea? Kumbuka kutoka Equation\ ref {eq20} kwamba

\[V_p = k\sum \dfrac{q_i}{r_i}.\]

Tunaweza kutibu usambazaji wa malipo unaoendelea kama mkusanyiko wa pointi za mtu binafsi zinazojitenga. Hii mavuno muhimu

\[V_p = \int \dfrac{dq}{r}\]

kwa uwezo katika hatua P. Kumbuka kwamba\(r\) ni umbali kutoka kwa kila mtu binafsi katika usambazaji wa malipo hadi hatua P. Kama tulivyoona katika Mashtaka ya Umeme na Mashamba, mashtaka ya infinitesimal hutolewa na

\[\underbrace{dq = \lambda \, dl}_{one \, dimension}\]

\[\underbrace{dq = \sigma \, dA}_{two \, dimensions}\]

\[\underbrace{dq = \rho \, dV \space}_{three \, dimensions}\]

ambapo\(\lambda\) ni linear malipo wiani,\(\sigma\) ni malipo kwa kila eneo la kitengo, na\(\rho\) ni malipo kwa kila kitengo kiasi.

Mfano\(\PageIndex{4}\): Potential of a Line of Charge

Pata uwezo wa umeme wa waya wa kushtakiwa kwa usawa, usio na conductive na wiani wa mstari\(\lambda\) (coulomb/mita) na urefu L kwa hatua ambayo iko kwenye mstari unaogawanya waya katika sehemu mbili sawa.

Mkakati

Ili kuanzisha tatizo, tunachagua kuratibu za Cartesian kwa njia ya kutumia ulinganifu katika tatizo iwezekanavyo. Tunaweka asili katikati ya waya na kuelekeza y -axis kando ya waya ili mwisho wa waya iko\(y = \pm L/2\). Sehemu ya shamba P iko kwenye ndege ya xy na tangu uchaguzi wa axes ni juu yetu, tunachagua x -axis kupitisha hatua ya shamba P, kama inavyoonekana kwenye Mchoro\(\PageIndex{6}\).

Kielelezo\(\PageIndex{6}\): Tunataka kuhesabu uwezo wa umeme kutokana na mstari wa malipo.

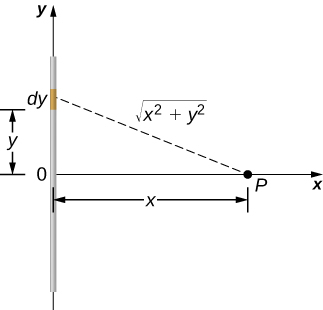
Suluhisho

Fikiria kipengele kidogo cha usambazaji wa malipo kati ya y na\(y + dy\). Malipo katika kiini hiki ni\(dq = \lambda \, dy\) na umbali kutoka kiini hadi hatua ya shamba P ni\(\sqrt{x^2 + y^2}\). Kwa hiyo, uwezo unakuwa

\[\begin{align} V_p &= k \int \dfrac{dq}{r} \nonumber \\[4pt] &= k\int_{-L/2}^{L/2} \dfrac{\lambda \, dy}{\sqrt{x^2 + y^2}} \nonumber \\[4pt] &= k\lambda \left[ln \left(y + \sqrt{y^2 + x^2}\right) \right]_{-L/2}^{L/2} \nonumber \\[4pt] &= k\lambda \left[ ln \left(\left(\dfrac{L}{2}\right) + \sqrt{\left(\dfrac{L}{2}\right)^2 + x^2}\right) - ln\left(\left(-\dfrac{L}{2}\right) + \sqrt{\left(-\dfrac{L}{2}\right)^2 + x^2}\right)\right] \nonumber \\[4pt] &= k\lambda ln \left[ \dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right]. \nonumber \end{align} \nonumber\]

Umuhimu

Kumbuka kuwa hii ilikuwa rahisi zaidi kuliko tatizo sawa kwa uwanja wa umeme, kutokana na matumizi ya kiasi kikubwa. Kumbuka kwamba tunatarajia kiwango cha sifuri cha uwezekano wa kuwa katika infinity, wakati tuna malipo ya mwisho. Kuchunguza hili, tunachukua kikomo cha uwezo hapo juu kama x inakaribia infinity; katika kesi hii, maneno ndani ya logi ya asili mbinu moja, na hivyo mbinu uwezo sifuri katika kikomo hiki. Kumbuka kwamba tunaweza kuwa amefanya tatizo hili equivalently katika kuratibu cylindrical; athari tu itakuwa mbadala r kwa x na z kwa y.

Mfano\(\PageIndex{5}\): Potential Due to a Ring of Charge

Pete ina wiani wa malipo ya sare\(\lambda\), na vitengo vya coulomb kwa mita ya kitengo cha arc. Pata uwezo wa umeme kwa hatua kwenye mhimili unaopita katikati ya pete.

Mkakati

Tunatumia utaratibu huo kama kwa waya iliyoshtakiwa. Tofauti hapa ni kwamba malipo yanasambazwa kwenye mduara. Tunagawanya mduara ndani ya vipengele vidogo vyenye umbo kama arcs kwenye mduara na kutumia kuratibu za cylindrical zilizoonyeshwa kwenye Mchoro\(\PageIndex{7}\).

Kielelezo\(\PageIndex{7}\): Tunataka kuhesabu uwezo wa umeme kutokana na pete ya malipo.

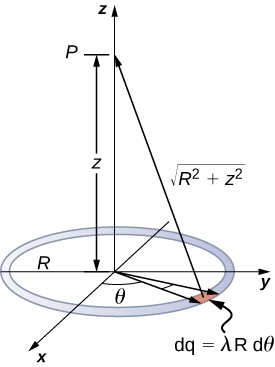
Suluhisho

Kipengele cha jumla cha arc kati\(\theta\) na\(\theta + d\theta\) ni ya urefu\(Rd\theta\) na kwa hiyo ina malipo sawa na\(\lambda Rd\theta\). Kipengele ni umbali wa\(\sqrt{z^2 + R^2}\) kutoka P, na hivyo uwezekano ni

\[\begin{align} V_p &= k\int \dfrac{dq}{r} \nonumber \\[4pt] &= k \int_0^{2\pi} \dfrac{\lambda Rd\theta}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= \dfrac{k \lambda R}{\sqrt{z^2 + R^2}} \int_0^{2\pi} d\theta \nonumber \\[4pt] &= \dfrac{2\pi k \lambda R}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}}. \nonumber \end{align} \nonumber\]

Umuhimu

Matokeo haya yanatarajiwa kwa sababu kila kipengele cha pete kina umbali sawa kutoka hatua P. Uwezo wa wavu katika P ni ule wa malipo ya jumla yaliyowekwa umbali wa kawaida,\(\sqrt{z^2 + R^2}\).

Mfano\(\PageIndex{6}\): Potential Due to a Uniform Disk of Charge

Disk ya radius R ina wiani wa malipo ya sare\(\sigma\) na vitengo vya mita ya coulomb mraba. Pata uwezo wa umeme wakati wowote kwenye mhimili unaopita katikati ya diski.

Mkakati

Sisi kugawanya disk katika seli pete umbo, na kufanya matumizi ya matokeo kwa pete kazi nje katika mfano uliopita, kisha kuunganisha juu r pamoja na\(\theta\). Hii inavyoonekana katika Kielelezo\(\PageIndex{8}\).

Kielelezo\(\PageIndex{8}\): Tunataka kuhesabu uwezo wa umeme kutokana na disk ya malipo.

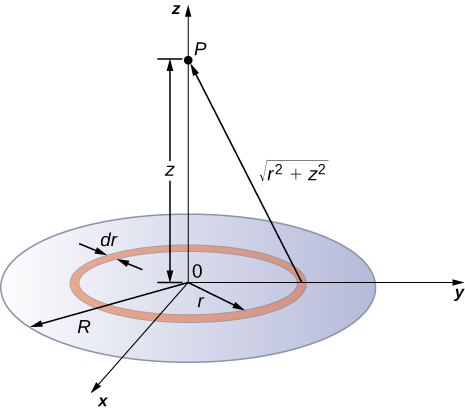
Suluhisho

Infinitesimal upana kiini kati ya cylindrical kuratibu r na\(r + dr\) inavyoonekana katika Kielelezo\(\PageIndex{8}\) itakuwa pete ya mashtaka ambao uwezo umeme\(dV_p\) katika hatua shamba ina kujieleza yafuatayo:

\[dV_p = k \dfrac{dq}{\sqrt{z^2 + r^2}}\]

wapi

\[dq = \sigma 2\pi r dr.\]

Uwezo wa uwezo wa pete zote za infinitesimal ambazo hufanya diski hutoa uwezo wavu katika hatua P. Hii imekamilika kwa kuunganisha kutoka\(r = 0\) kwa\(r = R\):

\[\begin{align} V_p &= \int dV_p = k2\pi \sigma \int_0^R \dfrac{r \, dr}{\sqrt{z^2 + r^2}}, \nonumber \\[4pt] &= k2\pi \sigma ( \sqrt{z^2 + R^2} - \sqrt{z^2}).\nonumber \end{align} \nonumber\]

Umuhimu

utaratibu wa msingi kwa ajili ya disk ni kwanza kuunganisha karibu na kisha juu ya r. Hii imeonyeshwa kwa wiani wa malipo ya sare (mara kwa mara). Mara nyingi, wiani wa malipo utatofautiana na r, na kisha muhimu ya mwisho itatoa matokeo tofauti.

Mfano\(\PageIndex{7}\): Potential Due to an Infinite Charged Wire

Pata uwezo wa umeme kutokana na waya wa kushtakiwa kwa muda mrefu sana.

Mkakati

Kwa kuwa tayari tumefanya uwezo wa waya wa mwisho wa urefu L katika Mfano\(\PageIndex{4}\), tunaweza kushangaa ikiwa kuchukua\(L \rightarrow \infty\) matokeo yetu ya awali yatafanya kazi:

\[V_p = \lim_{L \rightarrow \infty} k \lambda \ln \left(\dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right).\]

Hata hivyo, kikomo hiki haipo kwa sababu hoja ya logarithm inakuwa [2/0] kama\(L \rightarrow \infty\), hivyo njia hii ya kutafuta V ya waya usio haifanyi kazi. Sababu ya tatizo hili inaweza kufuatiliwa na ukweli kwamba mashtaka hayajawekwa ndani ya nafasi fulani, lakini kuendelea na infinity katika mwelekeo wa waya. Kwa hiyo, dhana yetu (isiyojulikana) kwamba uwezo wa sifuri lazima uwe umbali usio na kipimo kutoka kwa waya hauna halali tena.

Ili kuepuka ugumu huu katika kuhesabu mipaka, hebu tutumie ufafanuzi wa uwezo kwa kuunganisha juu ya uwanja wa umeme kutoka sehemu ya awali, na thamani ya uwanja wa umeme kutoka kwa usanidi huu wa malipo kutoka kwa sura iliyopita.

Suluhisho

Tunatumia muhimu

\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]

ambapo R ni umbali wa mwisho kutoka mstari wa malipo, kama inavyoonekana kwenye Mchoro\(\PageIndex{9}\).

Kielelezo\(\PageIndex{9}\): Pointi ya riba kwa kuhesabu uwezekano wa mstari usio na kipimo wa malipo.

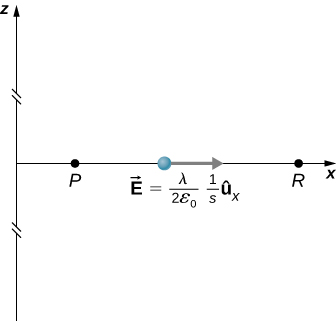
Pamoja na kuanzisha hii, tunatumia\(\vec{E}_p = 2k \lambda \dfrac{1}{s} \hat{s}\) na\(d\vec{l} = d\vec{s}\) kupata

\[\begin{align} V_p - V_R &= - \int_R^p 2k\lambda \dfrac{1}{s}ds \nonumber \\[4pt] &= -2 k \lambda \ln\dfrac{s_p}{s_R}. \nonumber \end{align} \nonumber\]

Sasa, kama sisi define uwezo kumbukumbu\(V_R = 0\) katika\(s_R = 1 \, m\), hii simplifies kwa

\[V_p = -2 k\lambda \, \ln \, s_p.\]

Kumbuka kuwa fomu hii ya uwezo inatumika kabisa; ni 0 saa 1 m na haijulikani kwa infinity, ndiyo sababu hatukuweza kutumia mwisho kama kumbukumbu.

Umuhimu

Ingawa kuhesabu uwezo wa moja kwa moja inaweza kuwa rahisi sana, tumepata tu mfumo ambao mkakati huu haufanyi kazi vizuri. Katika hali hiyo, kurudi kwenye ufafanuzi wa uwezo katika suala la uwanja wa umeme inaweza kutoa njia ya mbele.

Zoezi\(\PageIndex{7}\)

Je! Ni uwezekano gani kwenye mhimili wa pete isiyo ya kawaida ya malipo, ambapo wiani wa malipo ni\(\lambda (\theta) = \lambda \, \cos \, \theta\)?

Suluhisho

Itakuwa sifuri, kama ilivyo kwenye pointi zote kwenye mhimili, kuna mashtaka sawa na kinyume sawa sawa na kiwango cha riba. Kumbuka kuwa usambazaji huu utakuwa, kwa kweli, una wakati wa dipole.