7.3: Uwezo wa Umeme na Tofauti ya uwezo

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza uwezo wa umeme, voltage, na tofauti
• Eleza elektroni-volt
• Tumia uwezo wa umeme na tofauti tofauti kutoka kwa nishati na uwanja wa umeme
• Eleza mifumo ambayo elektroni-volt ni kitengo muhimu
• Tumia uhifadhi wa nishati kwa mifumo ya umeme

Kumbuka kwamba mapema sisi defined uwanja umeme kuwa wingi huru ya malipo ya mtihani katika mfumo fulani, ambayo hata hivyo kuruhusu sisi kuhesabu nguvu ambayo matokeo ya malipo holela mtihani. (Dhana ya msingi kwa kutokuwepo kwa taarifa nyingine ni kwamba malipo ya mtihani ni chanya.) Tulifafanua kwa ufupi shamba la mvuto, lakini mvuto daima huvutia, wakati nguvu ya umeme inaweza kuwa ya kuvutia au ya kutisha. Kwa hiyo, ingawa nishati ya uwezo ni ya kutosha kabisa katika mfumo wa mvuto, ni rahisi kufafanua kiasi kinachotuwezesha kuhesabu kazi kwa malipo bila kujitegemea ukubwa wa malipo. Kuhesabu kazi moja kwa moja inaweza kuwa vigumu, kwa kuwa\(W = \vec{F} \cdot \vec{d}\) na mwelekeo na ukubwa wa\(\vec{F}\) inaweza kuwa ngumu kwa mashtaka mengi, kwa vitu visivyo na kawaida, na kwa njia za kiholela. Lakini tunajua kwamba kwa sababu\(\vec{F}\), kazi, na hivyo\(\Delta U\) ni sawia na malipo ya mtihani\(q\). Ili kuwa na wingi wa kimwili ambao ni huru ya malipo ya mtihani, tunafafanua uwezo wa umeme\(V\) (au tu uwezo, kwa kuwa umeme unaeleweka) kuwa nishati ya uwezo kwa malipo ya kitengo:

Uwezo wa umeme

Nishati ya uwezo wa umeme kwa malipo ya kitengo ni

\[V = \dfrac{U}{q}. \label{eq-1}\]

Kwa kuwa mimi ni sawia na q, utegemezi wa kufuta. Hivyo, V haitegemei q. Mabadiliko katika nishati uwezo\(\Delta U\) ni muhimu, hivyo sisi ni wasiwasi na tofauti katika uwezo au uwezo tofauti\(\Delta V\) kati ya pointi mbili, ambapo

Tofauti ya uwezo wa umeme

Tofauti ya uwezo wa umeme kati ya pointi A na B,\(V_B - V_A\) inaelezwa kuwa mabadiliko katika nishati ya uwezo wa malipo q iliyohamishwa kutoka A hadi B, imegawanywa na malipo. Units ya tofauti tofauti ni joules kwa coulomb, kutokana na jina volt (V) baada ya Alessandro Volta.

\[1 \, V = 1 \, J/C \label{eq0}\]

Neno la kawaida la voltage ni jina la kawaida kwa tofauti ya uwezo wa umeme. Kumbuka kwamba wakati wowote voltage inukuliwa, inaeleweka kuwa tofauti kati ya pointi mbili. Kwa mfano, kila betri ina vituo viwili, na voltage yake ni tofauti kati yao. Zaidi ya kimsingi, hatua unayochagua kuwa sifuri volts ni kiholela. Hii ni sawa na ukweli kwamba nishati ya uwezo wa mvuto ina sifuri ya kiholela, kama vile usawa wa bahari au labda sakafu ya ukumbi wa hotuba. Ni vyema kusisitiza tofauti kati ya tofauti tofauti na nishati ya uwezo wa umeme.

Tofauti ya uwezo na Nishati ya Uwezo wa umeme

Uhusiano kati ya tofauti tofauti (au voltage) na nishati ya uwezo wa umeme hutolewa na

\[\Delta V = \dfrac{\Delta U}{q} \label{eq1}\]

au

\[ \Delta U = q \Delta V. \label{eq2}\]

Voltage si sawa na nishati. Voltage ni nishati kwa malipo ya kitengo. Hivyo, betri ya pikipiki na betri ya gari inaweza kuwa na voltage sawa (kwa usahihi, tofauti sawa ya uwezo kati ya vituo vya betri), lakini moja huhifadhi nishati zaidi kuliko nyingine kwa sababu\(\Delta U = q\Delta V\). Betri ya gari inaweza kusonga malipo zaidi kuliko betri ya pikipiki, ingawa wote ni betri 12-V.

Mfano\(\PageIndex{1}\): Calculating Energy

Una betri ya pikipiki ya 12.0-V ambayo inaweza kusonga 5000 C ya malipo, na betri ya gari ya 12.0-V ambayo inaweza kusonga 60,000 C ya malipo. Ni kiasi gani cha nishati ambacho kila hutoa? (Fikiria kwamba thamani ya namba ya kila malipo ni sahihi kwa takwimu tatu muhimu.)

Mkakati

Kusema tuna betri ya 12.0-V inamaanisha kwamba vituo vyake vina tofauti ya uwezo wa 12.0-V. Wakati betri hiyo inaposababisha malipo, inaweka malipo kwa njia ya tofauti ya 12.0 V, na malipo hupewa mabadiliko katika nishati inayoweza sawa na\(\Delta U = q\Delta V\). Ili kupata pato la nishati, tunazidisha malipo yaliyohamishwa na tofauti tofauti.

Suluhisho

Kwa betri pikipiki,\(q = 5000 \, C\) na\(\Delta V = 12.0 \, V\). Nishati ya jumla iliyotolewa na betri ya pikipiki ni

\[\Delta U_{cycle} = (5000 \, C)(12.0 \, V) = (5000 \, C)(12.0 \, J/C) = 6.00 \times 10^4 \, J. \nonumber\]

Vile vile, kwa betri ya gari,\(q = 60,000 \, C\) na

\[\Delta U_{car} = (60,000 \, C)(12.0 \, V) = 7.20 \times 10^5 \, J. \nonumber\]

Umuhimu

Voltage na nishati ni kuhusiana, lakini sio kitu kimoja. Vipimo vya betri vinafanana, lakini nishati inayotolewa na kila mmoja ni tofauti kabisa. Betri ya gari ina inji kubwa zaidi ya kuanza kuliko pikipiki. Kumbuka pia kwamba kama betri imefunguliwa, baadhi ya nishati yake hutumiwa ndani na matone yake ya voltage ya terminal, kama vile wakati vichwa vya kichwa vinapungua kwa sababu ya betri ya gari iliyoharibika. Nishati inayotolewa na betri bado imehesabiwa kama ilivyo katika mfano huu, lakini sio nishati zote zinazopatikana kwa matumizi ya nje.

Zoezi\(\PageIndex{1}\)

Je, betri ya 1.5-V AAA ina nishati ngapi ambayo inaweza kusonga 100 C?

Jibu

\(\Delta U = q\Delta V = (100 \, C)(1.5 \, V) = 150 \, J\)

Kumbuka kwamba nguvu zilizohesabiwa katika mfano uliopita ni maadili kamili. Mabadiliko katika nishati ya uwezo wa betri ni hasi, kwani inapoteza nishati. Betri hizi, kama mifumo mingi ya umeme, kwa kweli hoja hasi malipo elektroni hasa. Betri hurudia elektroni kutoka kwenye vituo vyao vya hasi (A) kupitia mzunguko wowote unaohusika na kuwavutia kwenye vituo vyao vyema (B), kama inavyoonekana kwenye Mchoro\(\PageIndex{1}\). Mabadiliko katika uwezo ni\(\Delta V = V_B - V_A = +12 \, V\) na malipo q ni hasi, hivyo hiyo\(\Delta U = q \Delta V\) ni hasi, maana ya nishati ya betri imepungua wakati q imehamia kutoka A hadi B.

Kielelezo\(\PageIndex{1}\): Betri husababisha malipo hasi kutoka kwa terminal yake hasi kupitia kichwa cha kichwa kwenye terminal yake nzuri. Mchanganyiko sahihi wa kemikali katika mashtaka tofauti ya betri ili terminal hasi ina ziada ya malipo hasi, ambayo inakabiliwa na hayo na kuvutia malipo mazuri kwenye terminal nyingine. Kwa suala la uwezo, terminal chanya iko kwenye voltage ya juu kuliko terminal hasi. Ndani ya betri, mashtaka mazuri na hasi huenda.

Mfano\(\PageIndex{2}\): How Many Electrons Move through a Headlight Each Second?

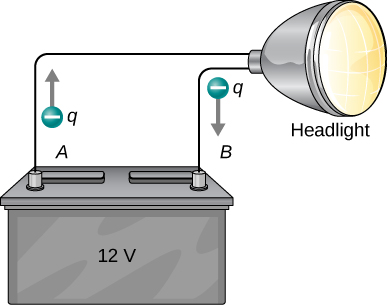
Wakati betri ya gari la 12.0-V inaimarisha kichwa kimoja cha 30.0-W, ni elektroni ngapi zinazopitia kila pili?

Mkakati

Ili kupata idadi ya elektroni, lazima kwanza kupata malipo ambayo huenda katika 1.00 s. malipo wakiongozwa ni kuhusiana na voltage na nishati kwa njia ya equations\(\Delta U = q \Delta V\). Taa ya 30.0-W inatumia joules 30.0 kwa pili. Kwa kuwa betri inapoteza nishati, tuna\(\Delta U = - 30 \, J\) na, kwa kuwa elektroni zinatoka kwenye terminal hasi kwa chanya, tunaona hiyo\(\Delta V = +12.0 \, V\).

Suluhisho

Ili kupata malipo q wakiongozwa, sisi kutatua equation\(\Delta U = q\Delta V\):

\[q = \dfrac{\Delta U}{\Delta V}.\]

Kuingia maadili kwa\(\Delta U\) na\(\Delta V\), tunapata

\[q = \dfrac{-30.0 \, J}{+12.0 \, V} = \dfrac{-30.0 \, J}{+12.0 \, J/C} = -2.50 \, C.\]

Idadi ya elektroni\(n_e\) ni chaji ya jumla iliyogawanywa na chaji kwa elektroni. Hiyo ni,

\[n_e = \dfrac{-2.50 \, C}{-1.60 \times 10^{-19} C/e^-} = 1.56 \times 10^{19} \, electrons.\]

Umuhimu

Hii ni idadi kubwa sana. Haishangazi kwamba hatuwezi kuchunguza elektroni binafsi na wengi wanapo katika mifumo ya kawaida. Kwa kweli, umeme ulikuwa unatumika kwa miongo mingi kabla ya kuamua kuwa mashtaka ya kusonga katika hali nyingi yalikuwa hasi. Malipo mazuri yanayohamia katika mwelekeo kinyume cha malipo hasi mara nyingi hutoa athari zinazofanana; hii inafanya kuwa vigumu kuamua ni ipi inayohamia au kama wote wanahamia.

Zoezi\(\PageIndex{2}\)

Ni elektroni ngapi zingeweza kupitia taa ya 24.0-W?

Jibu

\(-2.00 \, C, \, n_e = 1.25 \times 10^{19} \, electrons\)

Electroni-Volt

Nishati kwa kila elektroni ni ndogo sana katika hali za macroscopic kama ile katika mfano uliopita-sehemu ndogo ya joule. Lakini kwa kiwango kidogo, nishati hiyo kwa chembe (elektroni, proton, au ion) inaweza kuwa ya umuhimu mkubwa. Kwa mfano, hata sehemu ndogo ya joule inaweza kuwa kubwa ya kutosha kwa chembe hizi kuharibu molekuli za kikaboni na kuharibu tishu zilizo hai. Chembe inaweza kufanya uharibifu wake kwa mgongano wa moja kwa moja, au inaweza kuunda X-rays hatari, ambayo inaweza pia kuharibu. Ni muhimu kuwa na kitengo cha nishati kinachohusiana na madhara ya submicroscopic.

Kielelezo\(\PageIndex{2}\) kinaonyesha hali inayohusiana na ufafanuzi wa kitengo hicho cha nishati. Electron inaharakisha kati ya sahani mbili za kushtakiwa za chuma, kama inaweza kuwa katika tube ya televisheni ya zamani au oscilloscope. Electroni inapata nishati ya kinetiki ambayo baadaye inabadilishwa kuwa aina nyingine—mwanga katika tube ya televisheni, kwa mfano. (Kumbuka kuwa katika suala la nishati, “kuteremka” kwa elektroni ni “kupanda” kwa malipo mazuri.) Kwa kuwa nishati ni kuhusiana na voltage na\(\Delta U = q\Delta V\), tunaweza kufikiria joule kama coulomb-volt.

Kielelezo\(\PageIndex{2}\): kawaida elektroni bunduki kuchochea kasi elektroni kwa kutumia tofauti uwezo kati ya sahani mbili kutengwa chuma. Kwa uhifadhi wa nishati, nishati ya kinetic ina sawa na mabadiliko katika nishati inayoweza, hivyo\(KE = qV\). Nishati ya elektroni katika volts ya elektroni ni sawa na voltage kati ya sahani. Kwa mfano, tofauti ya 5000-V inazalisha elektroni 5000-EV. Kujenga dhana, yaani sahani mbili sambamba na shimo moja, inavyoonekana katika (a), wakati bunduki halisi ya elektroni inavyoonekana katika (b).

Kitengo cha Electroni-Volt

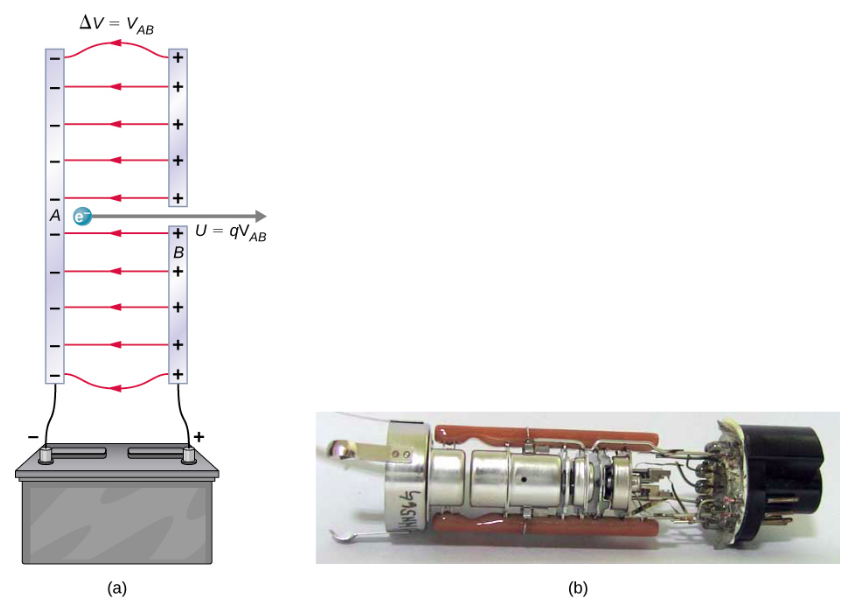
Kwa kiwango kidogo cha microscopic, ni rahisi zaidi kufafanua kitengo cha nishati kinachoitwa elektroni-volt (eV), ambayo ni nishati iliyotolewa kwa malipo ya msingi ya kasi kwa njia ya tofauti ya uwezo wa 1 V.

\[1 \, eV = (1.60 \times 10^{-19} C)(1 \, V) = (1.60 \times 10^{-19} C)(1 \, J/C) = 1.60 \times 10^{-19} \, J.\]

Electron iliharakisha kupitia tofauti tofauti ya 1 V inapewa nishati ya 1 eV. Inafuata kwamba elektroni iliharakisha kupitia 50 V inapata 50 eV. Tofauti ya uwezo wa 100,000 V (100 kV) inatoa elektroni nishati ya 100,000 eV (100 kV), na kadhalika. Vile vile, ioni yenye malipo mazuri mara mbili imeongezeka kwa njia ya 100 V inapata 200 eV ya nishati. Mahusiano haya rahisi kati ya kuharakisha mashtaka ya voltage na chembe hufanya elektroni-volt kitengo rahisi na rahisi cha nishati katika hali kama hizo.

Electron-volt ni kawaida kuajiriwa katika michakato submicroscopic- kemikali valence nguvu na Masi na nyuklia kisheria nguvu ni miongoni mwa wingi mara nyingi walionyesha katika elektroni-volts. Kwa mfano, kuhusu 5 eV ya nishati inahitajika kuvunja molekuli fulani za kikaboni. Ikiwa protoni imeharakisha kutoka kupumzika kupitia tofauti ya uwezo wa kV 30, inapata nishati ya kV 30 (30,000 eV) na inaweza kuvunja zaidi ya 6000 ya molekuli hizi\((30,000 \, eV \, : \, 5 \, eV \, per \, molecule = 6000 \, molecules)\). Nguvu za kuoza nyuklia ni kwa utaratibu wa MeV 1 (1,000,000 eV) kwa tukio na hivyo zinaweza kuzalisha uharibifu mkubwa wa kibiolojia.

Uhifadhi wa Nishati

Nishati ya jumla ya mfumo imehifadhiwa ikiwa hakuna kuongeza wavu (au kuondoa) kutokana na kazi au uhamisho wa joto. Kwa nguvu za kihafidhina, kama nguvu ya umeme, uhifadhi wa nishati inasema kwamba nishati ya mitambo ni mara kwa mara.

Nishati ya mitambo ni jumla ya nishati ya kinetic na nishati ya uwezo wa mfumo; yaani,\(K + U = constant\). Hasara ya U kwa chembe iliyoshtakiwa inakuwa ongezeko la K yake. Uhifadhi wa nishati ni alisema katika fomu equation kama

\[K + U = constant\]au\[K_i + U_i = K_f + U_f\]

ambapo i na f kusimama kwa hali ya awali na ya mwisho. Kama tulivyopata mara nyingi kabla, kuzingatia nishati inaweza kutupa ufahamu na kuwezesha kutatua tatizo.

Mfano\(\PageIndex{3}\): Electrical Potential Energy Converted into Kinetic Energy

Tumia kasi ya mwisho ya elektroni ya bure iliharakisha kutoka kwa kupumzika kupitia tofauti tofauti ya 100 V. (Fikiria kwamba thamani hii ya namba ni sahihi kwa takwimu tatu muhimu.)

Mkakati

Tuna mfumo na nguvu tu za kihafidhina. Kwa kuzingatia elektroni imeharakisha katika utupu, na kukataa nguvu ya mvuto (tutaangalia dhana hii baadaye), nishati yote ya uwezo wa umeme inabadilishwa kuwa nishati ya kinetic. Tunaweza kutambua aina ya awali na ya mwisho ya nishati kuwa

\(K_i = 0\),\(K_f = \frac{1}{2}mv^2\),\(U_i = qV\),\(U_f = 0\).

Suluhisho

Uhifadhi wa nishati inasema kwamba

\[K_i + U_i = K_f + U_f.\]

Kuingia fomu zilizotambuliwa hapo juu, tunapata

\[qV = \dfrac{mv^2}{2}.\]

Sisi kutatua hili kwa v:

\[v = \sqrt{\dfrac{2qV}{m}}.\]

Kuingia maadili kwa q, V, na m hutoa

\[v = \sqrt{\dfrac{2(-1.60 \times 10^{-19}C)(-100 \, J/C)}{9.11 \times 10^{-31} kg}} = 5.93 \times 10^6 \, m/s.\]

Umuhimu

Kumbuka kwamba malipo yote na voltage ya awali ni hasi, kama katika Kielelezo\(\PageIndex{2}\). Kutokana na majadiliano ya malipo ya umeme na uwanja wa umeme, tunajua kwamba vikosi vya umeme kwenye chembe ndogo kwa ujumla ni kubwa sana ikilinganishwa na nguvu ya mvuto. Kasi kubwa ya mwisho inathibitisha kwamba nguvu ya mvuto ni kweli kidogo hapa. Kasi kubwa pia inaonyesha jinsi ilivyo rahisi kuharakisha elektroni na voltages ndogo kwa sababu ya molekuli yao ndogo sana. Voltages juu sana kuliko 100 V katika tatizo hili ni kawaida kutumika katika bunduki elektroni. Vikwazo hivi vya juu vinazalisha kasi ya elektroni kubwa sana kwamba madhara kutoka kwa relativity maalum lazima izingatiwe na itajadiliwa mahali pengine. Ndiyo sababu tunazingatia voltage ya chini (kwa usahihi) katika mfano huu.

Zoezi\(\PageIndex{3}\)

Mfano huu utabadilishaje na positron? Positroni inafanana na elektroni isipokuwa chaji ni chanya.

Jibu

Itakuwa kwenda katika mwelekeo kinyume, bila athari juu ya mahesabu kama ilivyowasilishwa.

Voltage na Umeme shamba

Hadi sasa, tumechunguza uhusiano kati ya voltage na nishati. Sasa tunataka kuchunguza uhusiano kati ya voltage na uwanja wa umeme. Tutaanza na kesi ya jumla kwa\(\vec{E}\) shamba lisilo sare. Kumbuka kwamba formula yetu ya jumla ya nishati ya uwezo wa malipo ya mtihani q katika hatua P kuhusiana na hatua ya kumbukumbu R ni

\[U_p = - \int_R^p \vec{F} \cdot d\vec{l}.\]

Wakati sisi badala katika ufafanuzi wa uwanja wa umeme\((\vec{E} = \vec{F}/q)\), hii inakuwa

\[U_p = -q \int_R^p \vec{E} \cdot d\vec{l}.\]

Kutumia ufafanuzi wetu wa\((V = U/q)\) uwezo wa nishati hii uwezo, tunaona kwamba, kwa ujumla,

\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}.\]

Kutoka kwa majadiliano yetu ya awali ya nishati ya uwezo wa malipo katika uwanja wa umeme, matokeo yake ni huru ya njia iliyochaguliwa, na hivyo tunaweza kuchukua njia muhimu ambayo ni rahisi zaidi.

Fikiria kesi maalum ya malipo mazuri q katika asili. Kuhesabu uwezo unaosababishwa na q kwa umbali r kutoka kwa asili ya jamaa na kumbukumbu ya 0 kwa infinity (kumbuka kwamba tulifanya hivyo kwa nishati ya uwezo), basi\(P = r\) na\(R = \infty\),\(d\vec{l} = d\vec{r} = \hat{r}dr\) na kutumia\(\vec{E} = \frac{kq}{r^2} \hat{r}\). Wakati sisi kutathmini muhimu

\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]kwa mfumo huu, tuna

\[V_r = - \int_{\infty}^r \dfrac{kq}{r^2} dr = \dfrac{kq}{r} - \dfrac{kq}{\infty} = \dfrac{kq}{r}.\]

Matokeo haya,

\[V_r = \dfrac{kq}{r}\]

ni aina ya kiwango cha uwezo wa malipo ya uhakika. Hii itachunguzwa zaidi katika sehemu inayofuata.

Kuchunguza kesi nyingine ya kuvutia maalum, tuseme uwanja wa umeme sare\(\vec{E}\) huzalishwa kwa kuweka tofauti tofauti (au voltage)\(\Delta V\) kwenye sahani mbili za chuma zinazofanana, zilizoandikwa A na B (Kielelezo\(\PageIndex{3}\)). Kuchunguza hali hii itatuambia nini voltage inahitajika ili kuzalisha nguvu fulani za shamba la umeme. Pia itaonyesha uhusiano wa msingi zaidi kati ya uwezo wa umeme na uwanja wa umeme.

Kielelezo\(\PageIndex{3}\): Uhusiano kati ya V na E kwa sahani zinazofanya sambamba ni\(E = V/d\). (Kumbuka kuwa\(\Delta V = V_{AB}\) kwa ukubwa. Kwa malipo ambayo huhamishwa kutoka sahani A kwa uwezo mkubwa wa sahani B kwa uwezo wa chini, ishara ndogo inahitaji kuingizwa kama ifuatavyo:\(- \Delta V = V_A - V_B = V_{AB}\).)

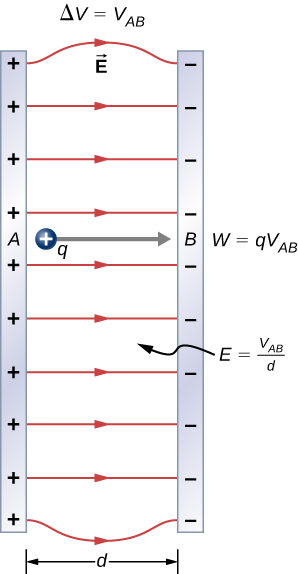
Kutoka kwa mtazamo wa mwanafizikia, ama\(\Delta V\) au\(\vec{E}\) inaweza kutumika kuelezea mwingiliano wowote kati ya mashtaka. Hata hivyo,\(\Delta V\) ni kiasi kikubwa na haina mwelekeo, ambapo\(\vec{E}\) ni kiasi cha vector, kuwa na ukubwa na mwelekeo. (Kumbuka kwamba ukubwa wa shamba la umeme, kiasi cha scalar, kinawakilishwa na E.) Uhusiano kati\(\Delta V\) na\(\vec{E}\) umefunuliwa kwa kuhesabu kazi iliyofanywa na nguvu ya umeme katika kusonga malipo kutoka hatua A hadi hatua B. Lakini, kama ilivyoelezwa hapo awali, mgawanyo wa malipo ya kiholela unahitaji calculus. Kwa hiyo tunaangalia uwanja wa umeme sare kama kesi maalum ya kuvutia.

Kazi iliyofanywa na uwanja wa umeme katika Kielelezo\(\PageIndex{3}\) ili kuhamisha malipo mazuri q kutoka A, sahani nzuri, uwezo wa juu, kwa B, sahani hasi, uwezo wa chini, ni

\[W = - \Delta U = - q\Delta V.\]

Tofauti tofauti kati ya pointi A na B ni

\[- \Delta V = - (V_B - V_A) = V_A - V_B = V_{AB}.\]

Kuingia hii katika kujieleza kwa mazao ya kazi

\[W = qV_{AB}.\]

Kazi ni\(W = \vec{F} \cdot \vec{d} = Fd \, cos \, \theta\): hapa\(cos \, \theta = 1\), kwa kuwa njia ni sawa na shamba. Hivyo,\(W = Fd\). Tangu\(F = qE\) tunaona kwamba\(W = qEd\).

Kubadilisha maneno haya kwa ajili ya kazi katika equation uliopita inatoa

\[qEd = qV_{AB}.\]

Malipo yanafuta, kwa hiyo tunapata kwa voltage kati ya pointi A na B.

Katika sare E-shamba tu:\[V_{AB} = Ed\]\[E = \dfrac{V_{AB}}{d}\] ambapo d ni umbali kutoka A hadi B, au umbali kati ya sahani katika Kielelezo\(\PageIndex{3}\). Kumbuka kuwa equation hii ina maana kwamba vitengo vya uwanja wa umeme ni volts kwa mita. Tayari tunajua vitengo kwa ajili ya uwanja wa umeme ni newtons kwa coulomb; hivyo, uhusiano zifuatazo kati ya vitengo ni halali:

\[1 \, N/C = 1 \, V/m.\]

Zaidi ya hayo, tunaweza kupanua hii kwa fomu muhimu. Kubadilisha Equation\ ref {eq1} katika ufafanuzi wetu kwa tofauti tofauti kati ya pointi A na B, tunapata

\[V_{AB} = V_B - V_A = - \int_R^B \vec{E} \cdot d\vec{l} + \int_R^A \vec{E} \cdot d\vec{l}\]

ambayo simplifies

\[V_B - V_A = - \int_A^B \vec{E} \cdot d\vec{l}.\]

Kama maandamano, kutokana na hili tunaweza kuhesabu tofauti tofauti kati ya pointi mbili (A na B) equidistant kutoka malipo ya uhakika q katika asili, kama inavyoonekana katika Kielelezo\(\PageIndex{4}\).

Kielelezo\(\PageIndex{4}\): Arc kwa ajili ya kuhesabu tofauti kati ya pointi mbili ambazo ni sawa na malipo ya uhakika katika asili.

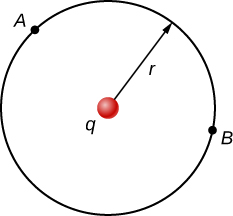
Ili kufanya hivyo, tunaunganisha karibu na arc ya mduara wa radius mara kwa mara r kati ya A na B, ambayo ina maana sisi basi\(d\vec{l} = r\hat{\varphi}d\varphi\), wakati wa kutumia\(\vec{E} = \frac{kq}{r^2} \hat{r}\). Hivyo,

\[\Delta V = V_B - V_A = - \int_A^B \vec{E} \cdot d\vec{l}.\]

kwa mfumo huu unakuwa

\[V_B - V_A = - \int_A^B \frac{kq}{r^2} \cdot r\hat{\varphi}d\varphi.\]

Hata hivyo,\(\hat{r} \cdot \hat{\varphi}\) na kwa hiyo

\[V_B - V_A = 0.\]

Matokeo haya, kwamba hakuna tofauti katika uwezo pamoja Radius mara kwa mara kutoka malipo uhakika, atakuja katika Handy wakati sisi ramani uwezekano.

Mfano\(\PageIndex{4A}\): What Is the Highest Voltage Possible between Two Plates?

Air kavu inaweza kusaidia nguvu ya juu ya uwanja wa umeme wa karibu\(3.0 \times 10^6 V/m\). Zaidi ya thamani hiyo, shamba hujenga ionization ya kutosha katika hewa ili kufanya hewa kuwa conductor. Hii inaruhusu kutokwa au cheche ambayo inapunguza shamba. Nini, basi, ni voltage ya juu kati ya sahani mbili zinazofanana zinazojitenga na 2.5 cm ya hewa kavu?

Mkakati

Tunapewa uwanja wa juu wa umeme E kati ya sahani na umbali d kati yao. Tunaweza kutumia equation\(V_{AB} = Ed\) kuhesabu voltage upeo.

Suluhisho

Tofauti tofauti au voltage kati ya sahani ni

\[V_{AB} = Ed.\]

Kuingia maadili yaliyotolewa kwa E na d inatoa

\[V_{AB} = (3.0 \times 10^6 V/m)(0.025 \, m) = 7.5 \times 10^4 \, V\]au\[V_{AB} = 75 \, kV.\]

(Jibu linalukuliwa kwa tarakimu mbili tu, kwa kuwa nguvu ya shamba ya juu ni takriban.)

Umuhimu

Moja ya matokeo ya matokeo haya ni kwamba inachukua karibu 75 kV kufanya cheche kuruka kwenye pengo la 2.5 cm (1-in.), au kV 150 kwa cheche ya 5-cm. Hii inapunguza vikwazo vinavyoweza kuwepo kati ya waendeshaji, labda kwenye mstari wa maambukizi ya nguvu. Voltage ndogo inaweza kusababisha cheche ikiwa kuna misuli juu ya uso, kwa kuwa pointi kali zina nguvu kubwa za shamba kuliko nyuso za laini. Humid hewa hupungua kwa nguvu ya chini ya shamba, maana yake ni kwamba voltage ndogo itafanya cheche kuruka kupitia hewa ya mvua. Vikwazo vikubwa vinaweza kujengwa na umeme wa tuli kwenye siku kavu (Kielelezo\(\PageIndex{5}\)).

Kielelezo\(\PageIndex{5}\): Chumba cha cheche kinatumiwa kufuatilia njia za chembe za juu-nishati. Ionization iliyoundwa na chembe wanapopitia gesi kati ya sahani inaruhusu cheche kuruka. Cheche ni perpendicular kwa sahani, kufuatia mistari ya uwanja wa umeme kati yao. Tofauti tofauti kati ya sahani zilizo karibu sio juu ya kutosha kusababisha cheche bila ionization zinazozalishwa na chembe kutoka kwa majaribio ya kasi (au mionzi ya cosmic). Aina hii ya detector sasa ni ya kizamani na haitumiki tena isipokuwa kwa madhumuni ya maandamano. (mikopo b: muundo wa kazi na Jack Collins)

Mfano\(\PageIndex{1B}\): Field and Force inside an Electron Gun

Bunduki ya elektroni (Kielelezo\(\PageIndex{2}\)) ina sahani sambamba zilizotengwa na cm 4.00 na hutoa elektroni 25.0 kV ya nishati. (a) Nguvu ya shamba la umeme kati ya sahani ni nini? (b) Je, shamba hili lingekuwa na nguvu gani kwenye kipande cha plastiki na\(0.500-\mu C\) malipo ambayo hupata kati ya sahani?

Mkakati

Kwa kuwa kujitenga kwa voltage na sahani hutolewa, nguvu za shamba za umeme zinaweza kuhesabiwa moja kwa moja kutoka kwa maneno\(E = \frac{V_{AB}}{d}\). Mara tu tunajua nguvu ya shamba la umeme, tunaweza kupata nguvu juu ya malipo kwa kutumia\(\vec{F} = q\vec{E}\). Kwa kuwa uwanja wa umeme ni katika mwelekeo mmoja tu, tunaweza kuandika equation hii kwa suala la ukubwa,\(F = qE\).

Suluhisho

a. kujieleza kwa ukubwa wa uwanja wa umeme kati ya sahani mbili sare chuma ni

\[E = \dfrac{V_{AB}}{d}.\]Kwa kuwa elektroni ni malipo moja na inapewa 25.0 kV ya nishati, tofauti ya uwezo lazima iwe 25.0 kV. Kuingia thamani hii\(V_{AB}\) na kujitenga sahani ya 0.0400 m, tunapata\[E = \frac{25.0 \, kV}{0.0400 \, m} = 6.25 \times 10^5 \, V/m.\]

b Ukubwa wa nguvu juu ya malipo katika uwanja wa umeme hupatikana kutoka kwa equation\[F = qE.\] Kubadilisha maadili inayojulikana hutoa

\[F = (0.500 \times 10^{-6}C)(6.25 \times 10^5 V/m) = 0.313 \, N.\]

Umuhimu Kumbuka kuwa vitengo ni newtons, tangu\(1 \, V/m = 1 \, N/C\). Kwa sababu shamba la umeme ni sare kati ya sahani, nguvu juu ya malipo ni sawa bila kujali ambapo malipo iko kati ya sahani.

Mfano\(\PageIndex{4C}\): Calculating Potential of a Point Charge

Kutokana na malipo ya uhakika\(q = +2.0-n C\) katika asili, uhesabu tofauti kati\(P_1\) ya uhakika umbali\(a = 4.0 \, cm\) kutoka q, na\(P_2\) umbali\(b = 12.0 \, cm\) kutoka q, ambapo pointi mbili zina angle\(\varphi = 24^o\) kati yao (Kielelezo\(\PageIndex{6}\)).

Kielelezo\(\PageIndex{6}\): Kupata tofauti katika uwezo kati\(P_1\) na\(P_2\).

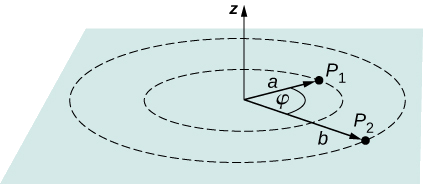
Mkakati Fanya hili kwa hatua mbili. Hatua ya kwanza ni kutumia\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) na kuruhusu\(A = a = 4.0 \, cm\) na\(B = b = 12.0 \, cm\),\(d\vec{l} = d\vec{r} = \hat{r}dr\) na\(\vec{E} = \frac{kq}{r^2} \hat{r}.\) kisha kufanya muhimu. Hatua ya pili ni kuunganisha\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) karibu arc ya r Radius mara kwa mara, ambayo ina maana sisi basi\(d\vec{l} = r\vec{\varphi}d\varphi\) na mipaka\(0 \leq \varphi \leq 24^o\), bado kutumia\(\vec{E} = \frac{kq}{r^2}\hat{r}\).

Kisha kuongeza matokeo mawili pamoja.

Solution Kwa sehemu ya kwanza,\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) kwa ajili ya mfumo huu inakuwa\(V_b - V_a = - \int_a^b \frac{kq}{r^2}\hat{r} \cdot \hat{r}dr\) ambayo computes kwa

\(\Delta V = - \int_a^b \frac{kq}{r^2}dr = kq \left[\frac{1}{a} - \frac{1}{b}\right]\)

\(= (8.99 \times 10^9 Nm^2/C^2)(2.0 \times 10^{-9}C) \left[\frac{1}{0.040 \, m} - \frac{1}{0.12 \, m}\right] = 300 \, V\).

Kwa hatua ya pili,\(V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\) inakuwa\(\Delta V = - \int_{0^o}^{24^o} \frac{kq}{r^2} \hat{r} \cdot r\hat{\varphi}d\varphi\), lakini\(\hat{r} \cdot \hat{\varphi} = 0\) na kwa hiyo\(\Delta V = 0\). Kuongeza sehemu mbili pamoja, tunapata 300 V.

Umuhimu

Tumeonyesha matumizi ya fomu muhimu ya tofauti ya uwezo ili kupata matokeo ya namba. Kumbuka kwamba, katika mfumo huu, tunaweza pia kutumia formula kwa uwezo kutokana na malipo ya uhakika katika pointi mbili na tu kuchukuliwa tofauti.

Zoezi\(\PageIndex{4}\)

Kutoka kwa mifano, nishati ya mgomo wa umeme hutofautiana na urefu wa mawingu kutoka chini? Fikiria mfumo wa wingu wa ardhi kuwa sahani mbili zinazofanana.

Jibu

Kutokana na nguvu ya juu ya shamba la umeme, uwezekano ambao mgomo hutokea huongezeka kwa urefu unaoongezeka juu ya ardhi. Kwa hiyo, kila elektroni itachukua nishati zaidi. Kuamua ikiwa kuna athari juu ya idadi ya elektroni iko katika siku zijazo.

Kabla ya kuwasilisha matatizo yanayohusisha electrostatics, tunashauri mkakati wa kutatua matatizo kufuata kwa mada hii.

Mkakati wa Kutatua matatizo: Electrostatics

1. Kuchunguza hali ili kuamua kama umeme wa tuli unahusishwa; hii inaweza kuhusisha mashtaka yaliyotengwa ya stationary, majeshi kati yao, na mashamba ya umeme wanayounda.
2. Tambua mfumo wa maslahi. Hii ni pamoja na kutambua idadi, maeneo, na aina ya mashtaka yanayohusika.
3. Tambua hasa kile kinachohitajika kuamua katika tatizo (kutambua haijulikani). Orodha iliyoandikwa ni muhimu. Kuamua kama nguvu ya Coulomb inapaswa kuchukuliwa moja kwa moja-ikiwa ni hivyo, inaweza kuwa na manufaa kuteka mchoro wa bure wa mwili, kwa kutumia mistari ya shamba la umeme.
4. Fanya orodha ya kile kinachopewa au kinaweza kuhitimishwa kutokana na tatizo kama ilivyoelezwa (kutambua maarifa). Ni muhimu kutofautisha nguvu ya Coulomb F kutoka uwanja wa umeme E, kwa mfano.
5. Kutatua equation sahihi kwa wingi kuamua (haijulikani) au kuteka mistari shamba kama ombi.
6. Kuchunguza jibu ili kuona kama ni busara: Je, ni mantiki? Je vitengo sahihi na idadi ya kushiriki busara?