7.2: Nishati ya uwezo wa umeme

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza kazi iliyofanywa na nguvu ya umeme
• Eleza nishati ya uwezo wa umeme
• Tumia kazi na uwezo wa nishati katika mifumo yenye mashtaka ya umeme

Wakati malipo ya bure ya bure yanaharakishwa na uwanja wa umeme, hutolewa nishati ya kinetic (Kielelezo\(\PageIndex{1}\)). Mchakato huo ni sawa na kitu kinachoharakishwa na uwanja wa mvuto, kama kwamba malipo yalikuwa yakishuka kilima cha umeme ambapo nishati yake ya uwezo wa umeme inabadilishwa kuwa nishati ya kinetic, ingawa bila shaka vyanzo vya nguvu ni tofauti sana. Hebu tuchunguze kazi iliyofanyika kwenye malipo q na uwanja wa umeme katika mchakato huu, ili tuweze kuendeleza ufafanuzi wa nishati ya umeme.

Kielelezo\(\PageIndex{1}\): Malipo yaliyoharakishwa na shamba la umeme ni sawa na wingi unaoshuka kilima. Katika hali zote mbili, uwezo wa nishati hupungua kama ongezeko la nishati ya kinetic,\(-\Delta U = \Delta K\). Kazi imefanywa kwa nguvu, lakini kwa kuwa nguvu hii ni kihafidhina, tunaweza kuandika\(W = -\Delta U\).

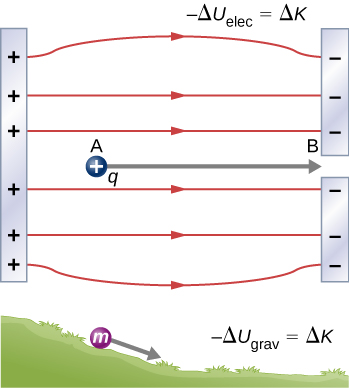
Nguvu ya umeme au Coulomb ni kihafidhina, ambayo ina maana kwamba kazi iliyofanywa kwenye q inajitegemea njia iliyochukuliwa, kama tutakavyoonyesha baadaye. Hii ni sawa na nguvu ya mvuto. Wakati nguvu ni kihafidhina, inawezekana kufafanua nishati inayohusishwa na nguvu. Kwa kawaida ni rahisi kufanya kazi na nishati inayoweza (kwa sababu inategemea tu nafasi) kuliko kuhesabu kazi moja kwa moja.

Ili kuonyesha hili kwa uwazi, fikiria malipo ya umeme\(+q\) yaliyowekwa kwenye asili na kuhamisha malipo mengine\(+Q\) kuelekea q kwa namna ambayo, kwa kila papo, nguvu iliyotumiwa\(\vec{F}\) inalingana na nguvu ya umeme\(\vec{F}_e\) kwenye Q (Kielelezo\(\PageIndex{2}\)). Kazi iliyofanywa na nguvu iliyotumiwa\(\vec{F}\) kwenye malipo Swali hubadilisha nishati ya uwezo wa Q. Tunaita nishati hii ya uwezo nishati ya umeme ya Q.

Kielelezo\(\PageIndex{2}\): Uhamisho wa malipo ya “mtihani” Swali mbele ya malipo ya “chanzo” cha kudumu q.

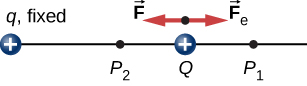
Kazi\(W_{12}\) iliyofanywa na nguvu iliyotumiwa\(\vec{F}\) wakati chembe inapoondoka\(P_1\) hadi\(P_2\) inaweza kuhesabiwa na

\[W_{12} = \int_{P_1}^{P_2} \vec{F} \cdot d\vec{l}.\]

Kwa kuwa nguvu iliyowekwa\(\vec{F}\) inalingana na nguvu ya umeme\(\vec{F}_e\) kwenye Q, majeshi mawili yana ukubwa sawa na maelekezo kinyume. Kwa hiyo, nguvu kutumika ni

\[\vec{F} = -\vec{F}_e = - \dfrac{kqQ}{r^2} \hat{r},\]

ambapo tuna defined chanya kuwa akizungumzia mbali na asili na r ni umbali kutoka asili. Maelekezo ya uhamisho wote na nguvu iliyotumiwa katika mfumo katika Kielelezo\(\PageIndex{2}\) ni sawa, na hivyo kazi iliyofanywa kwenye mfumo ni chanya.

Tunatumia barua U kuashiria nishati ya uwezo wa umeme, ambayo ina vitengo vya joules (J). Wakati nguvu ya kihafidhina inafanya kazi mbaya, mfumo unapata nishati inayoweza. Wakati nguvu ya kihafidhina inafanya kazi nzuri, mfumo unapoteza nishati inayoweza,\(\Delta U = - W\). Katika mfumo katika Kielelezo\(\PageIndex{3}\), nguvu ya Coulomb hufanya kinyume chake na uhamisho; kwa hiyo, kazi ni hasi. Hata hivyo, tumeongeza nishati ya uwezo katika mfumo wa malipo mawili.

Mfano\(\PageIndex{1}\): Kinetic Energy of a Charged Particle

\(+3.0-nC\)Malipo Q ni ya awali kupumzika umbali wa cm 10 (\(r_1\)) kutoka kwa\(+5.0-nC\) malipo q fasta katika asili (Kielelezo\(\PageIndex{3}\)). Kwa kawaida, nguvu ya Coulomb inaharakisha Q mbali na q, hatimaye kufikia cm 15 (\(r_2\)).

Kielelezo\(\PageIndex{3}\): Malipo Q yanakabiliwa na q, hivyo kuwa na kazi iliyofanyika juu yake na kupata nishati ya kinetic.

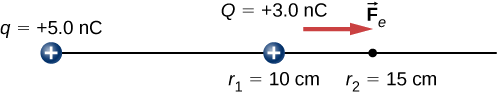
1. Ni kazi gani iliyofanywa na uwanja wa umeme kati\(r_1\) na\(r_2\)?
2. Je, ni kiasi gani cha nishati ya kinetic ambacho Q kina\(r_2\)?

Mkakati

Tumia kazi na ufafanuzi wa kawaida. Tangu Q ilianza kutoka kupumzika, hii ni sawa na nishati ya kinetic.

Suluhisho

Kuunganisha nguvu juu ya umbali, tunapata

\[\begin{align} W_{12} &= \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= \left. - \dfrac{kqQ}{r} \right|_{r_1}^{r_2} \nonumber \\[4pt] &= kqQ \left[\dfrac{-1}{r_2} + \dfrac{1}{r_1}\right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{-1}{0.15 \, m} + \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= 4.5 \times 10^{-7} \, J. \nonumber \end{align} \nonumber\]

Hii pia ni thamani ya nishati ya kinetic saa\(r_2\).

Umuhimu

Malipo ya Q ilikuwa awali ya kupumzika; uwanja wa umeme wa q ulifanya kazi kwenye Q, hivyo sasa Q ina nishati ya kinetic sawa na kazi iliyofanywa na shamba la umeme.

Zoezi\(\PageIndex{1}\)

Kama Q ina wingi wa\(4.00 \, \mu g\), ni nini kasi ya Q katika\(r_2\)?

Suluhisho

\(K = \frac{1}{2}mv^2\),\(v = \sqrt{2\frac{K}{m}} = \sqrt{2\frac{4.5 \times 10^{-7}J}{4.00 \times 10^{-9}kg}} = 15 \, m/s.\)

Katika mfano huu, kazi tuliyofanya ili kuharakisha malipo mazuri kutoka kwa kupumzika ni chanya na matokeo ya kupoteza kwa U, au hasi\(\Delta U\). Thamani ya U inaweza kupatikana wakati wowote kwa kuchukua hatua moja kama kumbukumbu na kuhesabu kazi inahitajika kuhamisha malipo kwa hatua nyingine.

Umeme uwezo wa Nishati

Kazi Tumefanya ili kuharakisha malipo mazuri kutoka kwa kupumzika ni chanya na matokeo ya kupoteza kwa U, au hasi\(\Delta U\). Kihisabati,

\[W = - \Delta U. \label{7.1}\]

Nishati ya uwezo wa nguvu na nishati ya uwezo wa umeme ni sawa kabisa. Uwezo wa nishati akaunti kwa ajili ya kazi iliyofanywa na nguvu kihafidhina na inatoa aliongeza ufahamu kuhusu nishati na nishati mabadiliko bila umuhimu wa kushughulika na nguvu moja kwa moja. Ni kawaida zaidi, kwa mfano, kutumia dhana ya nishati ya uwezo wa umeme kuliko kukabiliana na nguvu ya Coulomb moja kwa moja katika maombi halisi ya ulimwengu.

Katika kuratibu polar na q katika asili na Q iko katika r, makazi yao kipengele vector ni\(d\vec{l} = \hat{r} dr\) na hivyo kazi inakuwa

\[\begin{align} W_{12} &= kqQ \int_{r_1}^{r_2} \dfrac{1}{r^2} \hat{r} \cdot \hat{r} dr \nonumber \\[4pt] &= \underbrace{kqQ \dfrac{1}{r_2}}_{final \, point} - \underbrace{kqQ \dfrac{1}{r_1}}_{initial \,point}. \end{align}\]

Kumbuka kwamba matokeo haya inategemea tu endpoints na ni vinginevyo huru ya njia kuchukuliwa. Kuchunguza hili zaidi, kulinganisha njia ya\(P_1\)\(P_2\) na njia\(P_1 P_3 P_4 P_2\) katika Kielelezo\(\PageIndex{4}\).

\(\PageIndex{4}\)Kielelezo:Njia mbili kwa ajili ya makazi yao kwa\(P_1\).\(P_2\) Kazi ya makundi\(P_1P_3\) na\(P_4P_2\) ni sifuri kutokana na nguvu ya umeme kuwa perpendicular kwa uhamisho kando ya njia hizi. Kwa hiyo, kazi kwenye njia\(P_1P_2\) na\(P_1P_3P_4P_2\) ni sawa.

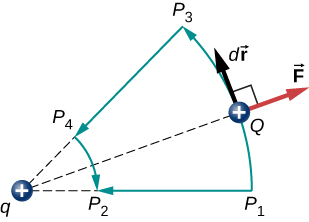
Makundi\(P_1P_3\) na\(P_4P_2\) ni arcs ya miduara unaozingatia q. Kwa kuwa nguvu ya Q inaelezea ama kuelekea au mbali na q, hakuna kazi inayofanywa kwa nguvu kusawazisha nguvu za umeme, kwa sababu ni perpendicular kwa uhamisho pamoja na arcs hizi. Kwa hiyo, kazi tu kufanyika ni pamoja sehemu\(P_3P_4\) ambayo ni sawa na\(P_1P_2\).

Moja ya maana ya hesabu hii ya kazi ni kwamba kama tungekuwa kwenda kuzunguka njia\(P_1P_3P_4P_2P_1\), kazi wavu itakuwa sifuri (Kielelezo\(\PageIndex{5}\)). Kumbuka kwamba hii ndio jinsi tunavyoamua kama nguvu ni kihafidhina au la. Kwa hiyo, kwa sababu nguvu ya umeme inahusiana na shamba la umeme na\(\vec{F} = g\vec{E}\), uwanja wa umeme ni yenyewe kihafidhina. Hiyo ni,

\[\oint \vec{E} \cdot d\vec{l} = 0.\]

Kumbuka kuwa Q ni mara kwa mara.

Kielelezo\(\PageIndex{5}\): Njia iliyofungwa katika uwanja wa umeme. Kazi ya wavu karibu na njia hii ni sifuri.

Mwingine maana ni kwamba tunaweza kufafanua uwezo wa umeme nishati. Kumbuka kwamba kazi iliyofanywa na nguvu ya kihafidhina pia imeelezwa kama tofauti katika nishati inayoweza kufanana na nguvu hiyo. Kwa hiyo, kazi ya\(W_{ref}\) kuleta malipo kutoka kwa hatua ya kumbukumbu hadi hatua ya riba inaweza kuandikwa kama

\[W_{ref} = \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}\]

na, kwa Equation\ ref {7.1}, tofauti katika nishati ya uwezo (\(U_2 - U_1\)) ya malipo ya mtihani Swali kati ya pointi mbili ni

\[\Delta U = - \int_{r_{ref}}^r \vec{F} \cdot d\vec{l}.\]

Kwa hiyo, tunaweza kuandika maneno ya jumla kwa nishati ya uwezo wa mashtaka mawili ya uhakika (katika kuratibu za spherical):

\[\Delta U = - \int_{r_{ref}}^r \dfrac{kqQ}{r^2}dr = -\left[-\dfrac{kqQ}{r}\right]_{r_{ref}}^r = kqQ\left[ \dfrac{1}{r} - \dfrac{1}{r_{ref}}\right].\]

Tunaweza kuchukua muda wa pili kuwa ngazi ya kumbukumbu ya mara kwa mara ya kiholela, ambayo hutumika kama kumbukumbu ya sifuri:

\[U(r) = k\dfrac{qQ}{r} - U_{ref}.\]

Uchaguzi rahisi wa kumbukumbu ambayo inategemea akili yetu ya kawaida ni kwamba wakati mashtaka mawili yamekuwa mbali sana, hakuna mwingiliano kati yao. (Kumbuka majadiliano ya nishati ya kumbukumbu uwezo katika Nishati Potential na Uhifadhi wa Nishati.) Kuchukua nishati uwezo wa hali hii kuwa sifuri kuondosha mrefu\(U_{ref}\) kutoka equation (kama vile wakati sisi kusema ardhi ni sifuri uwezo nishati katika mvuto uwezo tatizo nishati), na uwezo wa nishati ya Q wakati ni kutengwa na q kwa umbali au akubali fomu

\[\underbrace{U(r) = k\dfrac{qQ}{r}}_{zero \, reference \, at \, r = \infty}.\]

Fomu hii ni sawa na heshima\(q\) na\(Q\), hivyo ni bora kuelezewa kama nishati ya uwezo wa mfumo wa malipo mawili.

Mfano\(\PageIndex{2}\): Potential Energy of a Charged Particle

\(+3.0-nC\)Malipo Q ni ya awali kupumzika umbali wa cm 10\((r_1)\) kutoka kwa\(+5.0-nC\) malipo q fasta katika asili (Kielelezo\(\PageIndex{6}\)). Kwa kawaida, nguvu ya Coulomb huharakisha Q mbali na q, hatimaye kufikia cm 15\((r_2)\).

Kielelezo\(\PageIndex{6}\):\(Q\) Malipo yanakabiliwa na\(q\), hivyo kuwa na kazi iliyofanyika juu yake na kupoteza nishati.

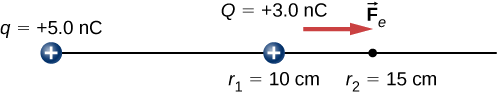
Je! Ni mabadiliko gani katika nishati ya uwezo wa mfumo wa malipo mawili kutoka\(r_1\) hadi\(r_2\)?

Mkakati

Tumia nishati yenye uwezo na ufafanuzi uliotolewa hapo juu:

\(\Delta U_{12} = -\int_{r_1}^{r_2} \vec{F} \cdot d\vec{r}\). Tangu Q ilianza kutoka kupumzika, hii ni sawa na nishati ya kinetic.

Suluhisho

Tuna

\[\begin{align} \Delta U_{12} &= - \int_{r_1}^{r_2} \vec{F} \cdot d\vec{r} \nonumber \\[4pt] &= - \int_{r_1}^{r_2} \dfrac{kqQ}{r^2}dr \nonumber \\[4pt] &= - \left[ - \dfrac{kqQ}{r}\right]_{r_1}^{r_2} \nonumber \\[4pt] &=kqQ \left[ \dfrac{1}{r_2} - \dfrac{1}{r_1} \right] \nonumber \\[4pt] &= (8.99 \times 10^9 \, Nm^2/C^2)(5.0 \times 10^{-9} C)(3.0 \times 10^{-9} C) \left[ \dfrac{1}{0.15 \, m} - \dfrac{1}{0.10 \, m}\right] \nonumber \\[4pt] &= - 4.5 \times 10^{-7} \, J. \end{align} \]

Umuhimu

Mabadiliko katika nishati ya uwezo ni hasi, kama inavyotarajiwa, na sawa na ukubwa kwa mabadiliko katika nishati ya kinetic katika mfumo huu. Kumbuka kutoka Mfano\(\PageIndex{1}\) kwamba mabadiliko katika nishati ya kinetic ilikuwa chanya.

Zoezi\(\PageIndex{2}\)

Nishati ya uwezo wa Q kuhusiana na kumbukumbu ya sifuri katika infinity\(r_2\) katika mfano hapo juu?

Suluhisho

Ina kinetic nishati ya\(4.5 \times 10^{-7} \, J\) katika hatua\(r_2\) na uwezo wa nishati ya\(9.0 \times 10^{-7} \, J\), ambayo ina maana kwamba kama Q mbinu infinity, nishati yake kinetic jumla mara tatu nishati kinetic katika\(r_2\), tangu wote wa nishati uwezo anapata kubadilishwa kwa kinetic.

Kutokana na sheria Coulomb ya, vikosi kutokana na mashtaka mbalimbali juu ya malipo mtihani\(Q\) superimpose; wanaweza kuwa mahesabu mmoja mmoja na kisha aliongeza. Hii ina maana kwamba kazi integrals na hivyo kusababisha uwezo uwezo kuonyesha tabia sawa. Ili kuonyesha hili, tunazingatia mfano wa kukusanyika mfumo wa mashtaka manne.

Mfano\(\PageIndex{3}\): Assembling Four Positive Charges

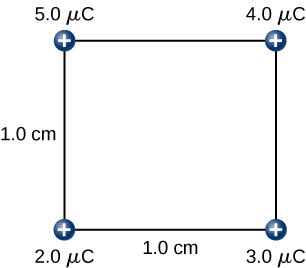
Pata kiasi cha kazi ambayo wakala wa nje lazima afanye katika kukusanya mashtaka manne\(+2.0-\mu C\)\(+3.0-\mu C\),\(+4.0-\mu C\) na\(+5.0-\mu C\) kwenye vichwa vya mraba wa upande wa 1.0 cm, kuanzia kila malipo kutoka kwa infinity (Kielelezo\(\PageIndex{7}\)).

Kielelezo\(\PageIndex{7}\): Ni kiasi gani cha kazi kinachohitajika ili kukusanyika usanidi huu wa malipo?

Mkakati

Tunaleta mashtaka moja kwa wakati, kuwapa maeneo ya kuanzia kwa infinity na kuhesabu kazi ya kuwaleta kutoka kwa infinity hadi eneo lao la mwisho. Tunafanya hivyo kwa utaratibu wa kuongeza malipo.

Suluhisho

Hatua ya 1. Kwanza kuleta\(+2.0-\mu C\) malipo kwa asili. Kwa kuwa hakuna mashtaka mengine kwa umbali wa mwisho kutoka kwa malipo haya bado, hakuna kazi inayofanyika kwa kuleta kutoka kwa infinity,

\[W_1 = 0.\]

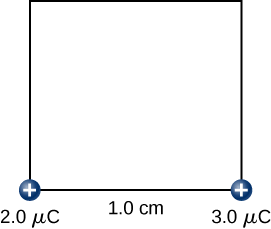
Hatua ya 2. Wakati wa kuweka\(+2.0-\mu C\) malipo yaliyowekwa katika asili, kuleta\(+3.0-\mu C\) malipo kwa\((x,y,z) = (1.0 \, cm, \, 0, \, 0)\) (Kielelezo\(\PageIndex{8}\)). Sasa, nguvu inayotumiwa inapaswa kufanya kazi dhidi ya nguvu inayotumiwa na\(+2.0-\mu C\) malipo yaliyowekwa katika asili. Kazi iliyofanywa sawa na mabadiliko katika nishati ya uwezo wa\(+3.0-\mu C\) malipo:

\[\begin{align} W_2 &= k\dfrac{q_1q_2}{r{12}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \dfrac{(2.0 \times 10^{-6} C)(3.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m} \nonumber \\[4pt] &= 5.4 \, J.\nonumber \end{align} \nonumber\]

Kielelezo\(\PageIndex{8}\): Hatua ya 2. Kazi\(W_2\) ya kuleta\(+3.0-\mu C\) malipo kutoka kwa infinity.

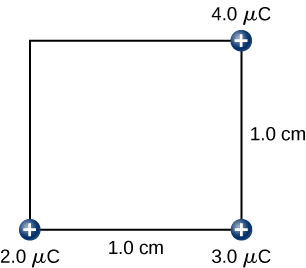
Hatua ya 3. Wakati wa kuweka mashtaka ya\(+2.0-\mu C\) na\(+3.0-\mu C\) fasta katika maeneo yao, kuleta\(+4.0-\mu C\) malipo kwa\((x,y,z) = (1.0 \, cm, \, 1.0 \, cm, \, 0)\) (Kielelezo)\(\PageIndex{9}\). Kazi iliyofanyika katika hatua hii ni

\[\begin{align} W_3 &= k\dfrac{q_1q_3}{r_{13}} + k \dfrac{q_2q_3}{r_{23}} \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right) \left[ \dfrac{(2.0 \times 10^{-6}C)(4.0 \times 10^{-6}C)}{\sqrt{2} \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2} m}\right] \nonumber \\[4pt] &= 15.9 \, J. \nonumber \end{align} \nonumber\]

Kielelezo\(\PageIndex{9}\): Hatua ya 3. Kazi ya\(W_3\) kuleta\(+4.0-\mu C\) malipo kutoka kwa infinity.

Hatua ya 4. Hatimaye, wakati wa kuweka mashtaka matatu ya kwanza katika maeneo yao, kuleta\(+5.0-\mu C\) malipo kwa\((x,y,z) = (0, \, 1.0 \, cm, \, 0)\) (Kielelezo\(\PageIndex{10}\)). Kazi iliyofanyika hapa ni

\[\begin{align} W_4 &= kq_4 \left[ \dfrac{q_1}{r_{14}} + \dfrac{q_2}{r_{24}} + \dfrac{q_3}{r_{34}}\right], \nonumber \\[4pt] &= \left(9.0 \times 10^9 \frac{N \cdot m^2}{C^2}\right)(5.0 \times 10^{-6}C) \left[ \dfrac{(2.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} + \dfrac{(3.0 \times 10^{-6} C)} {\sqrt{2} \times 10^{-2} m} + \dfrac{(4.0 \times 10^{-6}C)}{1.0 \times 10^{-2}m} \right] \nonumber \\[4pt] &= 36.5 \, J. \nonumber \end{align} \nonumber\]

Kielelezo\(\PageIndex{10}\): Hatua ya 4. Kazi ya\(W_4\) kuleta\(+5.0-\mu C\) malipo kutoka kwa infinity.

Kwa hiyo, kazi ya jumla iliyofanywa na nguvu iliyotumiwa katika kukusanya mashtaka manne ni sawa na jumla ya kazi katika kuleta kila malipo kutoka kwa infinity hadi nafasi yake ya mwisho:

\[\begin{align} W_T &= W_1 + W_2 + W_3 + W_4 \nonumber \\[4pt] &= 0 + 5.4 \, J + 15.9 \, J + 36.5 \, J \nonumber \\[4pt] &= 57.8 \, J. \nonumber \end{align} \nonumber\]

Umuhimu

Kazi ya kila malipo inategemea tu ushirikiano wake wa jozi na mashtaka mengine. Hakuna mwingiliano ngumu zaidi unaohitajika kuchukuliwa; kazi ya malipo ya tatu inategemea tu mwingiliano wake na mashtaka ya kwanza na ya pili, mwingiliano kati ya malipo ya kwanza na ya pili hauathiri ya tatu.

Zoezi\(\PageIndex{3}\)

Je! Nishati ya uwezo wa umeme ya mashtaka mawili ya uhakika ni chanya au hasi ikiwa mashtaka yana ishara sawa? Ishara kinyume? Hii inahusianaje na kazi muhimu ili kuleta mashtaka kwa ukaribu kutoka kwa infinity?

Suluhisho

chanya, hasi, na kiasi hiki ni sawa na kazi unayohitaji kufanya ili kuleta mashtaka kutoka kwa infinity

Kumbuka kuwa nishati ya uwezo wa umeme ni chanya ikiwa mashtaka mawili yana ya aina moja, ama chanya au hasi, na hasi ikiwa mashtaka mawili yana aina tofauti. Hii inafanya maana kama unafikiri ya mabadiliko katika nishati uwezo\(\Delta U\) kama wewe kuleta mashtaka mawili karibu au hoja yao mbali mbali. Kulingana na aina za jamaa za mashtaka, huenda ukafanya kazi kwenye mfumo au mfumo utakufanya kazi kwako, yaani, kazi yako ni chanya au hasi. Ikiwa unapaswa kufanya kazi nzuri kwenye mfumo (kwa kweli kushinikiza mashtaka karibu), basi nishati ya mfumo inapaswa kuongezeka. Ikiwa unaleta mashtaka mawili mazuri au mashtaka mawili hasi karibu, unapaswa kufanya kazi nzuri kwenye mfumo, ambayo inaleta uwezo wao wa nishati. Kwa kuwa nishati uwezo ni sawia na 1/r, nishati uwezo huenda juu wakati r huenda chini kati ya mbili chanya au mbili mashtaka hasi.

Kwa upande mwingine, ikiwa unaleta malipo mazuri na mabaya karibu, unapaswa kufanya kazi mbaya kwenye mfumo (mashtaka yanakuvuta), ambayo ina maana kwamba unachukua nishati mbali na mfumo. Hii inapunguza nishati uwezo. Kwa kuwa nishati ya uwezo ni hasi katika kesi ya jozi nzuri na hasi ya malipo, ongezeko la 1/r hufanya nishati inayoweza kuwa hasi zaidi, ambayo ni sawa na kupunguza nishati ya uwezo.

Matokeo kutoka kwa Mfano\(\PageIndex{2}\) yanaweza kupanuliwa kwa mifumo yenye idadi yoyote ya mashtaka. Katika kesi hii, ni rahisi zaidi kuandika formula kama

\[W_{12 . . . N} = \dfrac{k}{2} \sum_i^N \sum_j^N \dfrac{q_iq_j}{r_{ij}} \, for \, i \neq j.\]

Sababu ya 1/2 akaunti kwa kuongeza kila jozi ya mashtaka mara mbili.