6.E: Sheria ya Gauss (Mazoezi)

Last updated
Save as PDF

Page ID: 176127

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Maswali ya dhana

6.2 Umeme Flux

1. Jadili jinsi gani ingeelekeza uso wa eneo la eneo A katika uwanja wa umeme wa ukubwa wa\(\displaystyle E_0\) kupata

(a) kiwango cha juu na

(b) kiwango cha chini cha mtiririko kupitia eneo hilo.

2. Je! Ni maadili gani ya juu na ya chini ya mtiririko katika swali lililotangulia?

3. Flux ya umeme ya umeme inayovuka uso uliofungwa daima ni sifuri. Kweli au uongo?

4. Flux ya umeme ya umeme inayovuka uso wazi sio sifuri. Kweli au uongo?

6.3 Akifafanua Sheria ya Gauss

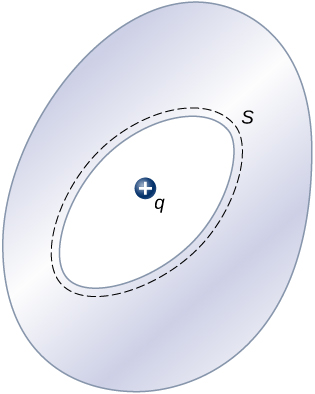
5. Mbili makini spherical nyuso enclosure uhakika malipo q. Radi ya nyanja ya nje ni mara mbili ya ndani. Linganisha fluxes umeme kuvuka nyuso mbili.

6. Linganisha mtiririko wa umeme kupitia uso wa mchemraba wa urefu wa upande a ambayo ina malipo q katikati yake hadi kuenea kwa njia ya uso wa mviringo wa radius a na malipo q katikati yake.

7. (a) Ikiwa umeme wa umeme kupitia uso uliofungwa ni sifuri, ni shamba la umeme lazima sifuri wakati wote juu ya uso?

(b) Ni malipo gani ya wavu ndani ya uso?

8. Jadili jinsi sheria Gauss itakuwa walioathirika kama uwanja umeme wa malipo uhakika hakuwa kutofautiana kama\(\displaystyle 1/r^2\).

9. Jadili kufanana na tofauti kati ya uwanja wa mvuto wa molekuli ya uhakika m na uwanja wa umeme wa malipo ya uhakika q.

10. Jadili kama sheria ya Gauss inaweza kutumika kwa vikosi vingine, na ikiwa ni hivyo, ni ipi.

11. Je! Neno\(\displaystyle \vec{E}\) katika sheria ya Gauss ni shamba la umeme linalozalishwa na malipo tu ndani ya uso wa Gaussia?

12. Kurekebisha sheria ya Gauss kwa kuchagua kitengo cha kawaida cha uso wa Gaussia kuwa moja iliyoelekezwa ndani.

6.4 Kutumia Sheria ya Gauss

13. Je, sheria ya Gauss itakuwa na manufaa kwa kuamua uwanja wa umeme wa mashtaka mawili sawa lakini kinyume umbali fasta mbali?

14. Jadili jukumu ambalo ulinganifu unavyofanya katika matumizi ya sheria ya Gauss. Kutoa mifano ya mgawanyo wa malipo ya kuendelea ambayo sheria ya Gauss ni muhimu na haifai katika kuamua uwanja wa umeme.

15. Jadili vikwazo kwenye uso wa Gaussia uliotumiwa kujadili ulinganifu wa mpango. Kwa mfano, urefu wake ni muhimu? Je, sehemu ya msalaba inapaswa kuwa mraba? Lazima nyuso za mwisho ziwe pande tofauti za karatasi?

6.5 Wafanyabiashara katika Msawazo wa umeme

16. Je, uwanja wa umeme ndani ya chuma daima sifuri?

17. Chini ya hali ya umeme, malipo ya ziada kwenye conductor hukaa juu ya uso wake. Je! Hii inamaanisha kwamba elektroni zote za conduction katika conductor ziko juu ya uso?

18. Malipo q huwekwa kwenye cavity ya conductor kama inavyoonyeshwa hapa chini. Je! Malipo nje ya kondakta hupata shamba la umeme kutokana na kuwepo kwa q?

Kielelezo kinaonyesha sura ya yai na cavity ya mviringo ndani yake. Cavity imezungukwa na mstari wa dotted nje yake. Hii ni kinachoitwa S. kuna malipo mazuri yaliyoandikwa q ndani ya cavity.

19. Kondakta katika takwimu iliyotangulia ina malipo ya ziada ya\(\displaystyle –5.0µC\). Ikiwa malipo ya\(\displaystyle 2.0-µC\) uhakika yanawekwa kwenye cavity, ni malipo gani ya wavu juu ya uso wa cavity na juu ya uso wa nje wa conductor?

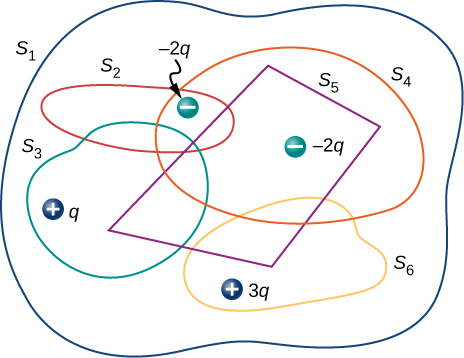
Matatizo

6.2 Umeme Flux

20. Sare uwanja wa umeme wa ukubwa\(\displaystyle 1.1×10^4N/C\) ni perpendicular kwa karatasi ya mraba na pande 2.0 m mrefu. Je, ni umeme gani kupitia karatasi?

21. Tumia mtiririko kupitia karatasi ya tatizo la awali ikiwa ndege ya karatasi iko kwenye pembe ya 60° hadi shamba. Pata mzunguko kwa maelekezo yote ya kitengo cha kawaida kwa karatasi.

22. Pata flux ya umeme kupitia eneo la mstatili 3cm×2cm kati ya sahani mbili sambamba ambapo kuna uwanja wa umeme wa mara kwa mara wa 30 N/C kwa mwelekeo wafuatayo wa eneo: (a) sambamba na sahani, (b) perpendicular kwa sahani, na (c) kawaida kwa eneo kufanya 30° angle na mwelekeo wa uwanja wa umeme. Kumbuka kwamba angle hii pia inaweza kutolewa kama 180°+30°.

23. Umeme wa umeme kupitia eneo la mraba wa upande wa cm 5 karibu na karatasi kubwa ya kushtakiwa\(\displaystyle 3×10^{−5}N⋅m^2/C\) hupatikana. wakati eneo hilo ni sawa na sahani. Pata wiani wa malipo kwenye karatasi.

24. Sahani mbili kubwa za alumini za mstatili za eneo\(\displaystyle 150cm^2\) zinakabiliana na kutenganishwa kwa mm 3 kati yao. Sahani zinashtakiwa kwa kiasi sawa cha mashtaka kinyume, ± 20μC. Mashtaka kwenye sahani yanakabiliana. Pata mtiririko kupitia mduara wa radius 3 cm kati ya sahani wakati kawaida kwa mduara hufanya angle ya 5° na mstari perpendicular kwa sahani. Kumbuka kwamba angle hii pia inaweza kutolewa kama 180°+5°.

25. Eneo la mraba la eneo\(\displaystyle 2cm^2\) liko katika nafasi ya uwanja wa umeme wa ukubwa\(\displaystyle 10^3N/C\). Kiasi cha mtiririko kwa njia hiyo inategemea jinsi mraba unavyoelekezwa kuhusiana na mwelekeo wa shamba la umeme. Pata mtiririko wa umeme kupitia mraba, wakati kawaida hufanya pembe zifuatazo na uwanja wa umeme: (a) 30°, (b) 90°, na (c) 0°. Kumbuka kuwa pembe hizi zinaweza pia kutolewa kama 180°+ν.

26. Shamba la vector linaelekezwa kando ya mhimili wa z,\ (\ displaystyle\ vec {v} =\ frac {α} {x^2+y ^ 2}\ kofia {z}.

(a) Pata mtiririko wa shamba la vector kupitia mstatili katika xy-ndege kati ya <x<ba<x<b na c<y<dc<y<d.

(b) Fanya vivyo hivyo kupitia mstatili katika ndege ya yz-kati ya <z<ba<z<b na c<y<dc<y<d. (Acha jibu lako kama muhimu.)

27. Fikiria shamba la umeme sare\(\displaystyle \vec{E} =(4.0\hat{j}+3.0\hat{k})×10^3N/C\). Je, ni umeme wake kupitia eneo la mviringo la radius 2.0 m ambalo liko katika ndege ya xy?

28. Kurudia tatizo la awali, kutokana na kwamba eneo la mviringo ni (a) katika yz -ndege na (b) 45° juu ya xy -ndege.

29. Waya usio na kipimo na malipo kwa urefu wa kitengo\(\displaystyle λ\) iko kwenye mhimili wa kati wa uso wa cylindrical wa radius r na urefu l. Je, ni flux kupitia uso kutokana na uwanja wa umeme wa waya kushtakiwa?

6.3 Akifafanua Sheria ya Gauss

30. Kuamua mtiririko wa umeme kupitia kila uso uliofungwa ambao sehemu ya msalaba ndani ya uso inavyoonyeshwa hapa chini.

31. Pata mzunguko wa umeme kupitia uso uliofungwa ambao sehemu za msalaba zinaonyeshwa hapa chini.

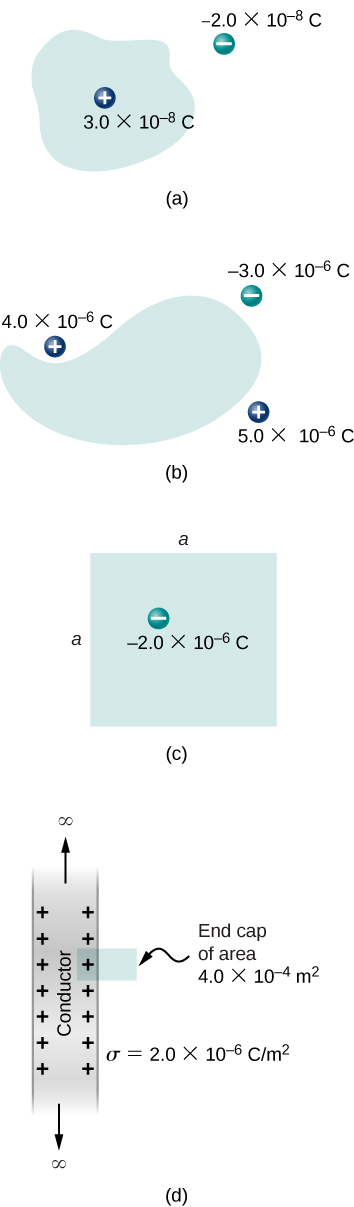
32. Malipo ya uhakika q iko katikati ya mchemraba ambao pande zake ni za urefu a. Ikiwa hakuna mashtaka mengine katika mfumo huu, ni nini umeme wa umeme kupitia uso mmoja wa mchemraba?

33. Malipo ya uhakika\(\displaystyle 10μC\) ni katika eneo lisilojulikana ndani ya mchemraba wa upande wa cm 2. Pata flux ya umeme ya wavu ingawa nyuso za mchemraba.

34. Flux ya wavu\(\displaystyle 1.0×10^4N⋅^m2/C\) inapita ndani kupitia uso wa eneo la radius 5 cm.

(a) Ni kiasi gani cha malipo ndani ya nyanja?

(b) Je, tunaweza kuamua eneo la malipo kutoka kwa habari hii?

35. Malipo q huwekwa kwenye moja ya pembe za mchemraba wa upande a, kama inavyoonyeshwa hapa chini. Pata ukubwa wa umeme wa umeme kwa njia ya uso uliovuliwa kutokana na q. Fikiria\(\displaystyle q>0\).

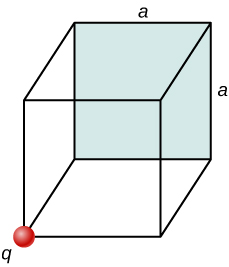
Kielelezo inaonyesha mchemraba na urefu wa kila upande sawa na. nyuma ya uso wake ni kivuli. Kona moja ya mbele ina mduara mdogo juu yake iliyoandikwa q.

36. Flux ya umeme kupitia sanduku la cubical 8.0 cm upande ni\(\displaystyle 1.2×10^3N⋅m^2/C\). Je, ni malipo ya jumla yaliyofungwa na sanduku?

37. Flux umeme kupitia uso spherical ni\(\displaystyle 4.0×10^4N⋅m^2/C\). Ni malipo gani ya wavu yaliyofungwa na uso?

38. Mchemraba ambao pande zake ni za urefu d huwekwa katika uwanja wa umeme wa ukubwa wa ukubwa\(\displaystyle E=4.0×10^3N/C\) ili shamba liwe na nyuso mbili za kinyume za mchemraba. Je, ni flux ya wavu kupitia mchemraba?

39. Kurudia tatizo la awali, kwa kuzingatia kwamba shamba la umeme linaelekezwa pamoja na diagonal ya mwili wa mchemraba.

40. Malipo ya jumla\(\displaystyle 5.0×10^{−6}C\) yanasambazwa kwa usawa katika kiasi cha cubical ambacho kando yake ni urefu wa 8.0 cm.

(a) Wiani wa malipo katika mchemraba ni nini?

(b) Je, ni umeme wa umeme kwa njia ya mchemraba na mviringo wa 12.0-cm ambayo ni makini na usambazaji wa malipo?

(d) Je, ni mtiririko wa umeme kwa njia ya uso wa mviringo wa radius 3.0 cm ambayo pia ni makini na usambazaji wa malipo?

6.4 Kutumia Sheria ya Gauss

41. Kumbuka kwamba katika mfano wa nyanja ya kushtakiwa sare,\(\displaystyle ρ_0=Q/(\frac{4}{3}πR^3)\). Andika upya majibu kwa suala la malipo ya jumla Swali kwenye nyanja.

42. Tuseme kwamba wiani wa malipo ya usambazaji wa malipo ya spherical umeonyeshwa kwenye Mchoro 6.23 ni\(\displaystyle ρ(r)=ρ_0r/R\) kwa\(\displaystyle r≤R\) na sifuri kwa\(\displaystyle r>R\). Pata maneno kwa uwanja wa umeme ndani na nje ya usambazaji.

43. muda mrefu sana, nyembamba waya ina sare linear malipo wiani wa\(\displaystyle 50μC/m\). Shamba la umeme ni umbali wa 2.0 cm kutoka waya?

44. Malipo ya\(\displaystyle −30μC\) inasambazwa kwa usawa katika kiasi cha spherical ya radius 10.0 cm. Kuamua uwanja wa umeme kutokana na malipo haya kwa umbali wa

(a) 2.0 cm,

(b) 5.0 cm, na

45. Kurudia mahesabu yako kwa tatizo lililotangulia, kutokana na kwamba malipo yanasambazwa sawasawa juu ya uso wa conductor spherical ya radius 10.0 cm.

46. Malipo ya jumla Q inasambazwa kwa usawa katika shell ya spherical ya radii ya ndani na nje\(\displaystyle r_1\) na\(\displaystyle r_2\), kwa mtiririko huo. Onyesha kwamba uwanja wa umeme kutokana na malipo ni

\(\displaystyle \vec{E} =\vec{0}\)\(\displaystyle (r≤r_1)\);

\(\displaystyle \vec{E} =\frac{Q}{4πε_0r^2}(\frac{r^3−r_1^3}{r_2^3−r_1^3})\hat{r}\)\(\displaystyle (r_1≤r≤r_2)\);

\(\displaystyle \vec{E} =\frac{Q}{4πε_0r^2}\hat{r}\)\(\displaystyle (r≥r_2)\).

47. Wakati malipo yanawekwa kwenye nyanja ya chuma, inaishia katika usawa kwenye uso wa nje. Tumia habari hii kuamua uwanja wa umeme wa\(\displaystyle +3.0μC\) malipo kuweka mpira wa alumini ya 5.0-cm spherical katika pointi mbili zifuatazo katika nafasi:

(a) uhakika 1.0 cm kutoka katikati ya mpira (hatua ya ndani) na

(b) uhakika 10 cm kutoka katikati ya mpira (hatua ya nje).

48. Karatasi kubwa ya malipo ina wiani wa malipo ya sare ya\(\displaystyle 10μC/m^2\). Shamba la umeme ni kutokana na malipo haya kwa hatua tu juu ya uso wa karatasi?

49. Kuamua kama ulinganifu wa cylindrical takriban unashikilia hali zifuatazo. Hali kwa nini au kwa nini.

(a) Fimbo ya shaba ya urefu wa 300 cm ya radius 1 cm inadaiwa na +500 nC ya malipo na tunatafuta uwanja wa umeme kwa hatua ya 5 cm kutoka katikati ya fimbo.

(b) Fimbo ya shaba ya urefu wa 10 cm ya radius 1 cm inadaiwa na +500 nC ya malipo na tunatafuta shamba la umeme kwa hatua ya 5 cm kutoka katikati ya fimbo.

(c) Fimbo ya mbao ya 150 cm inaunganishwa kwenye fimbo ya plastiki ya cm 150 ili kufanya fimbo ya urefu wa 300-cm, ambayo kisha hujenga rangi ya kushtakiwa ili mtu apate wiani wa malipo ya sare. Radi ya kila fimbo ni 1 cm, na tunatafuta shamba la umeme kwa hatua ambayo ni 4 cm kutoka katikati ya fimbo.

(d) Fimbo sawa na (c), lakini sisi kutafuta uwanja umeme katika hatua ambayo ni 500 cm kutoka katikati ya fimbo.

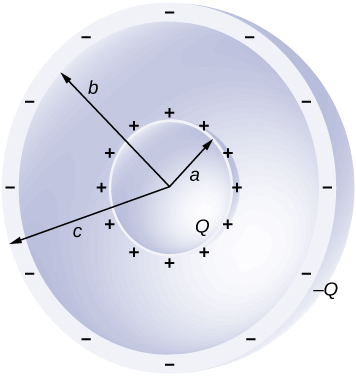
50. Fimbo ya fedha ndefu ya radius 3 cm ina malipo ya\(\displaystyle −5μC/cm\) juu ya uso wake.

(a) Pata shamba la umeme kwenye hatua ya 5 cm kutoka katikati ya fimbo (hatua ya nje).

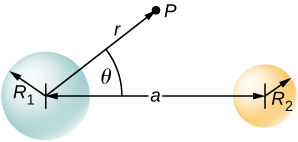
(b) Pata shamba la umeme kwenye hatua ya 2 cm kutoka katikati ya fimbo (hatua ya ndani).

51. Shamba la umeme katika cm 2 kutoka katikati ya fimbo ndefu ya shaba ya radius 1 cm ina ukubwa 3 N/C na kuelekezwa nje kutoka kwa mhimili wa fimbo.

(a) Ni kiasi gani cha malipo kwa urefu wa kitengo kilichopo kwenye fimbo ya shaba?

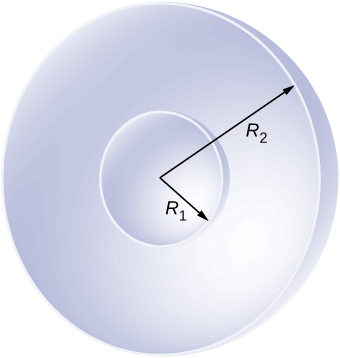
(b) Je, itakuwa umeme flux kupitia mchemraba wa upande 5 cm hali kama kwamba fimbo hupita kwa njia ya pande kinyume ya mchemraba perpendicularly?

52. Muda mrefu shaba cylindrical shell ya Radius ndani 2 cm na Radius nje 3 cm mazingira concentrically kushtakiwa muda mrefu alumini fimbo ya Radius 1 cm na malipo wiani wa 4 PC/m. mashtaka yote juu ya fimbo alumini kuishi katika uso wake. Uso wa ndani wa ganda la shaba una chaji kinyume kabisa na ule wa fimbo ya alumini ilhali uso wa nje wa ganda la shaba una chaji sawa na fimbo ya alumini. Pata ukubwa na mwelekeo wa uwanja wa umeme kwenye pointi zilizo katika umbali wafuatayo kutoka katikati ya fimbo ya alumini:

(a) 0.5 cm, (b) 1.5 cm, (c) 2.5 cm, (d) 3.5 cm, na (e) 7 cm.

53. Malipo yanasambazwa kwa usawa na wiani\(\displaystyle ρ\) katika kiasi kikubwa cha cylindrical cha radius R. Onyesha kwamba uwanja wa usambazaji huu malipo ni moja kwa moja radially kwa heshima na silinda na kwamba

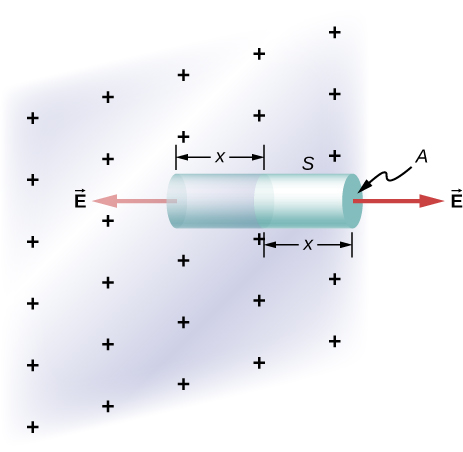
\(\displaystyle E=\frac{ρr}{2ε_0}\)\(\displaystyle (r≤R)\);

\(\displaystyle E=\frac{ρR^2}{2ε_0r}\)\(\displaystyle (r≥R)\)

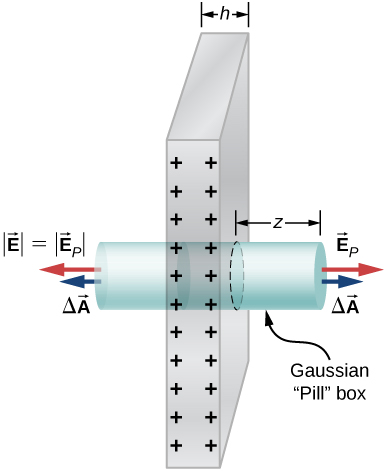
54. Malipo husambazwa katika kiasi cha muda mrefu sana cha cylindrical cha radius R kama wiani wa malipo huongezeka kwa umbali r kutoka mhimili wa kati wa silinda kulingana na\(\displaystyle ρ=αr\), wapi\(\displaystyle α\) mara kwa mara. Onyesha kwamba uwanja wa usambazaji huu malipo ni moja kwa moja radially kwa heshima na silinda na kwamba

\(\displaystyle E=\frac{αr^2}{3ε_0}\)\(\displaystyle (r≤R)\);

\(\displaystyle E=\frac{αR^3}{3ε_0r}\)\(\displaystyle (r≥R)\).

55. Sehemu ya umeme 10.0 cm kutoka kwenye uso wa mpira wa shaba wa radius 5.0 cm inaelekezwa kuelekea kituo cha mpira na ina ukubwa\(\displaystyle 4.0×10^2N/C\). Ni malipo gani juu ya uso wa mpira?

56. Malipo yanasambazwa katika shell ya mviringo ya radius ya ndani\(\displaystyle r_1\) na radius ya nje\(\displaystyle r_2\) na wiani wa kiasi kilichotolewa na\(\displaystyle ρ=ρ_0r_1/r\), wapi\(\displaystyle ρ_0\) mara kwa mara. Kuamua uwanja wa umeme kutokana na malipo haya kama kazi ya r, umbali kutoka katikati ya shell.

57. Malipo husambazwa kwa kiasi kikubwa cha radius R na wiani\(\displaystyle ρ=αr^2\), ambapo αα ni mara kwa mara. Kuamua shamba la umeme kutokana na malipo kwa pointi zote ndani na nje ya nyanja.

58. Fikiria kiini cha uranium kuwa nyanja ya radius\(\displaystyle R=7.4×10^{−15}m\) yenye malipo ya 92e kusambazwa kwa usawa katika kiasi chake. (a) Nguvu ya umeme inayotumiwa kwenye elektroni\(\displaystyle 3.0×10^{−15}m\) inapotoka katikati ya kiini? (b) Ni kasi gani ya elektroni katika hatua hii?

59. Uzito wa malipo ya kiasi cha usambazaji wa malipo ya spherical hutolewa na\(\displaystyle ρ(r)=ρ_0e^{−αr}\), wapi\(\displaystyle ρ_0\) na\(\displaystyle α\) ni mara kwa mara. Shamba la umeme linazalishwa na usambazaji huu wa malipo?

6.5 Wafanyabiashara katika Msawazo wa umeme

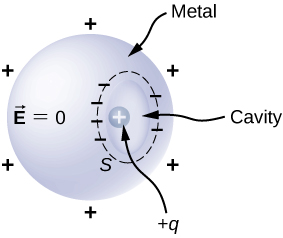
60. Kondakta asiyetiwa na cavity ya ndani inavyoonyeshwa kwenye takwimu ifuatayo. Tumia uso uliofungwa S pamoja na sheria ya Gaus ili kuonyesha kwamba wakati malipo q yamewekwa kwenye cavity malipo ya jumla -q yanaingizwa kwenye uso wa ndani wa kondakta. Je! Ni malipo gani kwenye uso wa nje wa kondakta?

Aina ya chuma yenye cavity inavyoonyeshwa. Ni kinachoitwa vector E sawa na sifuri. Kuna pamoja na ishara zinazozunguka. Kuna malipo mazuri yaliyoandikwa pamoja na q ndani ya cavity. Cavity imezungukwa na ishara ndogo. — Kielelezo 6.46: Malipo ndani ya cavity ya chuma. Malipo kwenye uso wa nje hayategemei jinsi mashtaka yanavyosambazwa kwenye uso wa ndani tangu shamba E ndani ya mwili wa chuma ni sifuri.

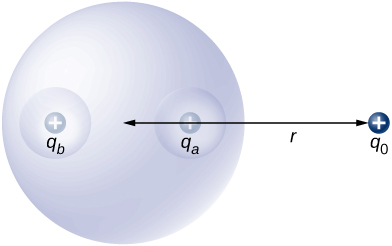
61. Conductor spherical S ya radius R ina cavities mbili spherical A na B ya radii a na b, kwa mtiririko huo kama inavyoonekana hapa chini. Mashtaka mawili ya uhakika\(\displaystyle +q_a\) na\(\displaystyle +q_b\) huwekwa katikati ya mizigo miwili kwa kutumia msaada usio na uendeshaji. Kwa kuongeza, malipo ya uhakika\(\displaystyle +q_0\) huwekwa nje kwa mbali r kutoka katikati ya nyanja.

(a) Chora mgawanyo wa malipo takriban katika chuma ingawa nyanja ya chuma haina malipo ya wavu.

(b) Chora mistari ya shamba la umeme. Chora mistari ya kutosha kuwakilisha maeneo yote tofauti.

Kielelezo kinaonyesha nyanja yenye mizigo miwili. Malipo mazuri a iko kwenye cavity moja na malipo mazuri qb iko kwenye cavity nyingine. Malipo mazuri q0 iko nje ya nyanja kwa umbali r kutoka katikati yake.

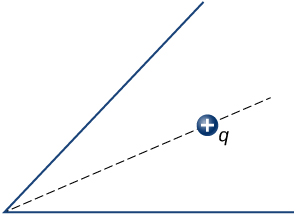
62. Chaji chanya uhakika ni kuwekwa katika bisector angle ya mbili uncharged ndege makondakta kwamba kufanya angle ya 45° .Angalia hapa chini. Chora mistari ya shamba la umeme.

Pembe ya papo hapo inavyoonyeshwa. Bisector yake ni mstari wa dotted. Malipo mazuri q yanaonyeshwa kwenye mstari wa dotted.

63. Silinda ndefu ya shaba ya radius 3 cm inashtakiwa ili iwe na malipo sare kwa urefu wa kitengo juu ya uso wake wa 3 C/m. (a) Pata shamba la umeme ndani na nje ya silinda. (b) Chora mistari ya uwanja wa umeme katika ndege perpendicular kwa fimbo.

64. Mpira wa alumini wa radius 4 cm unashtakiwa kwa 5μC ya malipo. Shell ya shaba ya shaba ya radius ya ndani 6 cm na radius ya nje 8 cm inaizunguka. Malipo ya jumla ya -8μC yanawekwa kwenye ganda la shaba.

(a) Kupata uwanja umeme katika maeneo yote katika nafasi, ikiwa ni pamoja na pointi ndani ya alumini na shaba shell wakati shaba shell na alumini nyanja ni makini.

(b) Pata shamba la umeme wakati wote katika nafasi, ikiwa ni pamoja na pointi ndani ya shell ya alumini na shaba wakati vituo vya shell ya shaba na nyanja ya alumini ni 1 cm mbali.

65. Silinda ndefu ya alumini ya mita za radius R inashtakiwa ili iwe na malipo sare kwa urefu wa kitengo juu ya uso wake wa\(\displaystyle λ\). (a) Pata shamba la umeme ndani na nje ya silinda. (b) Panda shamba la umeme kama kazi ya umbali kutoka katikati ya fimbo.

66. Katika uso wa conductor yoyote katika usawa wa umeme,\(\displaystyle E=σ/ε_0\). Onyesha kwamba equation hii inafanana na ukweli kwamba\(\displaystyle E=kq/r^2\) kwenye uso wa conductor spherical.

67. Sahani mbili zinazofanana 10 cm upande zinapewa mashtaka sawa na kinyume cha ukubwa\(\displaystyle 5.0×10^{−9}C\). Sahani ni 1.5 mm mbali. Shamba la umeme ni katikati ya kanda kati ya sahani?

68. Sahani mbili zinazofanana, kila sehemu ya sehemu ya msalaba\(\displaystyle 400cm^2\), ni 2.0 cm mbali na haijashughulikiwa. Ikiwa\(\displaystyle 1.0×10^{12}\) elektroni zinahamishwa kutoka sahani moja hadi nyingine, ni nini (a) wiani wa malipo kwenye kila sahani? (b) Uwanja wa umeme kati ya sahani?

69. Uzito wa malipo ya uso kwenye bomba la chuma la muda mrefu ni\(\displaystyle σ\). Shamba la umeme ni nje na ndani ya bomba? Tuseme bomba ina kipenyo cha 2a.

Kielelezo kinaonyesha bomba, na sehemu ya cylindrical iliyoonyeshwa. Mshale unaoelekeza juu na moja akizungumzia chini ya bomba kutoka silinda ni kinachoitwa infinity. Kuna pamoja na ishara ndani ya kuta za silinda.

70. Malipo ya uhakika\(\displaystyle q=−5.0×10^{−12}C\) huwekwa katikati ya shell ya uendeshaji wa mviringo wa radius ya ndani 3.5 cm na radius ya nje 4.0 cm. Shamba la umeme tu juu ya uso wa conductor linaelekezwa radially nje na ina ukubwa 8.0 N/C.

(a) Wiani wa malipo juu ya uso wa ndani wa shell ni nini?

(b) Wiani wa malipo kwenye uso wa nje wa shell ni nini?

71. Kondakta imara ya cylindrical ya radius a imezungukwa na shell ya cylindrical ya ndani ya radius Silinda imara na shell hubeba mashtaka +Q na -Q, kwa mtiririko huo. Kutokana kwamba urefu L wa waendeshaji wote ni mkubwa zaidi kuliko a au b, kuamua uwanja wa umeme kama kazi ya r, umbali kutoka kwa mhimili wa kawaida wa kati wa mitungi, kwa (a)\(\displaystyle r<a\); (b)\(\displaystyle a<r<b\); na (c)\(\displaystyle r>b\).

Matatizo ya ziada

72. Shamba la vector\(\displaystyle \vec{E}\) (sio lazima shamba la umeme; vitengo vya kumbuka) hutolewa na\(\displaystyle \vec{E} =3x^2\hat{k}\). Tumia\(\displaystyle ∫_S\vec{E}⋅\hat{n}da\), ambapo S ni eneo lililoonyeshwa hapa chini. Kudhani kwamba\(\displaystyle \hat{n}=\hat{k}\).

S mraba na urefu wa kila upande sawa na inavyoonekana katika ndege xy.

73. Rudia tatizo lililotangulia, kwa\(\displaystyle \vec{E} = 2x\hat{i}+3x^2\hat{k}\).

74. Eneo la mviringo S linajumuisha asili, lina radius a, na liko katika ndege ya yz. Mahesabu\(\displaystyle ∫_S\vec{E}⋅\hat{n}dA\) kwa ajili ya\(\displaystyle \vec{E} = 3z^2\hat{i}\).

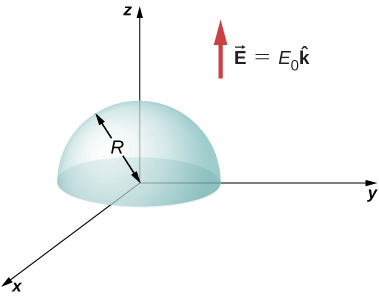
75. (a) Tumia mzunguko wa umeme kupitia uso wa wazi wa hemispherical kutokana na uwanja wa umeme\(\displaystyle \vec{E} = E_0\hat{k}\) (angalia hapa chini).

(b) Ikiwa hemisphere inazungushwa na 90° karibu na x -axis, ni flux gani kupitia hiyo?

Hemisphere yenye radius R inavyoonyeshwa na msingi wake katika ndege ya xy na katikati ya msingi katika asili. Mshale unaonyeshwa kando yake, kinachoitwa vector E sawa na kofia ya E0 k.

76. Tuseme kwamba uwanja wa umeme wa malipo ya pekee yalikuwa sawa na\(\displaystyle 1/r^{2+σ}\) badala ya\(\displaystyle 1/r^2\). Kuamua flux ambayo hupita kupitia uso wa nyanja ya radius R iliyozingatia malipo. Je, sheria Gauss kubaki halali?

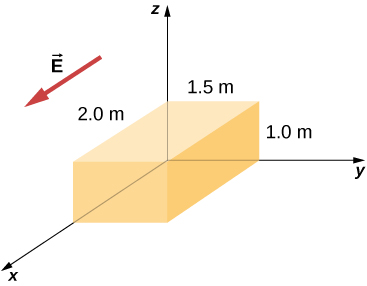
77. Shamba la umeme katika kanda linatolewa\(\displaystyle a=200N⋅m/C, b=2.0m,\) na\(\displaystyle \vec{E} =a/(b+cx)\hat{i}\), wapi\(\displaystyle c=2.0\) na.Ni malipo gani ya wavu yaliyofungwa na kiasi cha kivuli kilichoonyeshwa hapa chini?

Kielelezo kinaonyesha cuboid na kona moja juu ya asili ya safu za kuratibu. Urefu wake pamoja na mhimili x ni m 2, pamoja na mhimili y ni 1.5 m na kando ya mhimili ni m 1 Mshale nje ya pointi za cuboid kando ya mhimili x. Ni kinachoitwa vector E.

78. Mashtaka mawili sawa na kinyume ya ukubwa Q iko kwenye mhimili x- kwenye pointi +a na -a, kama inavyoonyeshwa hapa chini. ni flux wavu kutokana na mashtaka haya kwa njia ya uso mraba wa upande 2a ambayo ipo katika yz -ndege na ni katikati katika asili? (Kidokezo: Tambua mtiririko kwa sababu ya kila malipo tofauti, kisha utumie kanuni ya superposition. Unaweza kuwa na uwezo wa kufanya hoja ulinganifu.)

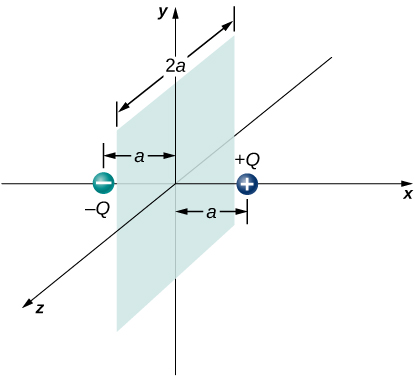
Mraba kivuli inavyoonekana katika ndege ya yz na kituo chake katika asili. Upande wake sambamba na mhimili z imeandikwa kuwa ya urefu 2a. malipo lebo pamoja Q ni umeonyesha kwenye chanya x mhimili katika umbali kutoka asili. Malipo yaliyoandikwa chini ya Q yanaonyeshwa kwenye mhimili hasi x umbali a kutoka kwa asili.

79. Mwanafunzi mwenzake alihesabu mtiririko kupitia mraba kwa mfumo katika tatizo lililotangulia na alipata 0. Nini kosa?

80. Kipande cha 10cm × 10cm cha foil ya alumini ya unene wa 0.1 mm ina malipo ya\(\displaystyle 20μC\) kuenea kwenye nyuso zote mbili za upande sawasawa. Unaweza kupuuza mashtaka kwenye pande nyembamba za kando.

(a) Pata wiani wa malipo.

(b) Pata uwanja wa umeme 1 cm kutoka katikati, ukichukua ulinganifu wa mpango wa takriban.

81. Vipande viwili vya 10cm × 10cm vya foil ya alumini ya unene 0.1 mm hukutana na kutenganishwa kwa mm 5. Moja ya foil ina malipo ya\(\displaystyle +30μC\) na nyingine ina\(\displaystyle −30μC\).

(a) Pata wiani wa malipo kwenye nyuso zote, yaani, juu ya wale wanaokabiliana na wale ambao wanakabiliwa mbali.

(b) Kupata uwanja umeme kati ya sahani karibu na kituo cha kuchukua planar ulinganifu.

82. Sahani mbili kubwa za shaba zinazokabiliana zina msongamano wa malipo\(\displaystyle ±4.0C/m^2\) juu ya uso unaoelekea sahani nyingine, na sifuri kati ya sahani. Pata mzunguko wa umeme kupitia eneo la mstatili wa 3cm×4cm kati ya sahani, kama inavyoonyeshwa hapo chini, kwa mwelekeo wafuatayo wa eneo hilo.

(a) Kama eneo ni sambamba na sahani, na

(b) ikiwa eneo hilo\(\displaystyle θ=30°\) linatokana na mwelekeo sambamba. Kumbuka, angle hii pia inaweza kuwa\(\displaystyle θ=180°+30°\).

Kielelezo kinaonyesha sahani mbili zinazofanana na mstari wa dotted hasa kati ya mbili, sawa nao. Sahani ya tatu huunda theta ya angle na mstari wa dotted.

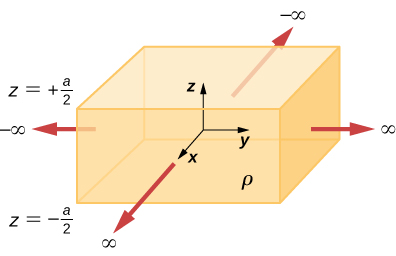
83. Slab isiyo na kipimo kati ya ndege iliyoelezwa\(\displaystyle z=−a/2\) na\(\displaystyle z=a/2\) ina wiani wa malipo ya kiasi cha sare\(\displaystyle ρ\) (angalia hapa chini). Shamba la umeme linazalishwa na usambazaji huu wa malipo, ndani na nje ya usambazaji?

Kielelezo kinaonyesha cuboid na kituo chake katika asili ya axes kuratibu. Mishale perpendicular kwa nyuso za uhakika cuboid nje. Mishale pamoja na shaba nzuri na y ni lebo infinity na mishale pamoja na x hasi na y axes ni lebo minus infinity. Cuboid inaitwa rho. Uso wake wa juu umeandikwa z sawa na pamoja na 2 na uso wake wa chini umeandikwa z sawa na minus a na 2.

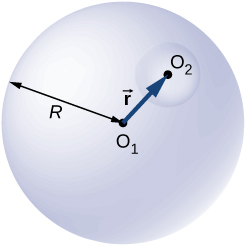
84. Malipo ya jumla Q inasambazwa kwa usawa katika kiasi cha spherical ambacho kinazingatia\(\displaystyle O_1\) na kina radius R. Bila kuvuruga malipo iliyobaki, malipo huondolewa kwenye kiasi cha spherical ambacho kinazingatia\(\displaystyle O_2\) (angalia hapa chini). Onyesha kwamba uwanja wa umeme kila mahali katika kanda tupu hutolewa na\(\displaystyle \vec{E} = \frac{Q\vec{r}}{4πε_0R^3}\), wapi\(\displaystyle \vec{r}\) vector makazi yao moja kwa moja kutoka\(\displaystyle O_1\) kwa\(\displaystyle O_2\).

Kielelezo kinaonyesha mduara na kituo cha O1 na radius R. mduara mwingine mdogo na kituo cha O2 inavyoonekana ndani yake. mshale kutoka O1 kwa O2 ni kinachoitwa vector r.

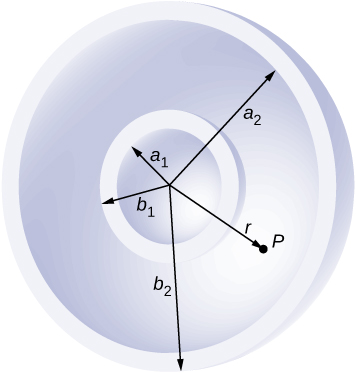
85. Non-conductive spherical shell ya Radius ndani\(\displaystyle a_1\) na radius nje\(\displaystyle b_1\) ni enhetligt kushtakiwa wiani\(\displaystyle ρ_1\) kushtakiwa ndani ya mwingine shell nonconductive spherical ya radius ndani na radius ya nje,\(\displaystyle b_2\) ambayo pia ni sawa\(\displaystyle a_2\)\(\displaystyle ρ_2\) Angalia hapa chini. Pata shamba la umeme kwenye hatua ya nafasi P umbali r kutoka kituo cha kawaida kama vile (a)\(\displaystyle r>b_2\), (b)\(\displaystyle a_2<r<b_2\), (c)\(\displaystyle b_1<r<a_2\), (d)\(\displaystyle a_1<r<b_1\), na (e)\(\displaystyle r<a_1\).

Kielelezo kinaonyesha shells mbili za mviringo. Radi ya ndani na nje ya ganda la ndani ni a1 na a2 mtawalia. Radi ya ndani na nje ya ganda la nje ni a2 na b2 mtawalia. umbali kutoka kituo cha uhakika P kati shells mbili kinachoitwa r.

86. Sehemu mbili zisizo za uendeshaji wa radii\(\displaystyle R_1\) na\(\displaystyle R_2\) zinashtakiwa kwa usawa na densities ya malipo\(\displaystyle ρ_1\) na\(\displaystyle ρ_2\), kwa mtiririko huo. Wao ni kutengwa katika kituo cha hadi kituo cha umbali a (angalia hapa chini). Pata uwanja wa umeme kwenye hatua P iko umbali r kutoka katikati ya nyanja 1 na iko katika mwelekeo\(\displaystyle θ\) kutoka kwenye mstari unaojiunga na nyanja mbili kuchukua msongamano wao wa malipo hauathiriwa na kuwepo kwa nyanja nyingine. (Kidokezo: Kazi nyanja moja kwa wakati na utumie kanuni ya superposition.)

duru mbili ni umeonyesha upande kwa upande na umbali kati ya vituo vyao kuwa. mduara kubwa ina Radius R1 na moja ndogo ina Radius R2. r mshale ni umeonyesha kutoka katikati ya mduara kubwa kwa uhakika P nje ya duruba. r aina theta angle kwa.

87. Disk ya radius R hukatwa kwenye sahani kubwa isiyo ya kufanya ambayo inashtakiwa kwa usawa na wiani wa malipo σ (coulomb kwa mita ya mraba). Angalia hapa chini. Pata shamba la umeme kwa urefu h juu ya katikati ya diski. (\(\displaystyle h>>R,h<<l\)au\(\displaystyle w\)). (kidokezo: Jaza shimo na\(\displaystyle ±σ\).)

88. Vipande vya mviringo vinavyofanya shells vinabeba mashtaka Q na -Q, kwa mtiririko huo (angalia hapa chini). Hifadhi ya ndani ina unene usio na maana. Kuamua shamba la umeme kwa (a)\(\displaystyle r<a;\) (b)\(\displaystyle a<r<b\); (c)\(\displaystyle b<r<c\); na (d)\(\displaystyle r>c\).

Sehemu ya shells mbili za mviringo zinaonyeshwa. Ni kinachoitwa Q na ina ishara pamoja na kuzunguka. Ganda la nje lina radius ya ndani b na radius ya nje c. inaitwa chini ya Q na ina ishara ndogo karibu nayo.

89. Imeonyeshwa hapa chini ni makundi mawili ya kuunganisha ya radii ya radii\(\displaystyle R_1\) na\(\displaystyle R_2\), kila moja ya unene wa mwisho sana kuliko radius yoyote. Hifadhi ya ndani na ya nje hubeba mashtaka ya wavu\(\displaystyle q_1\) na\(\displaystyle q_2\), kwa mtiririko huo, ambapo wote wawili\(\displaystyle q_1\) na\(\displaystyle q_2\) ni chanya. Shamba la umeme ni nini kwa (a)\(\displaystyle r<R_1\); (b)\(\displaystyle R_1<r<R_2\); na (c)\(\displaystyle r>R_2\)? (d) Ni malipo gani ya wavu juu ya uso wa ndani wa shell ya ndani, uso wa nje wa shell ya ndani, uso wa ndani wa shell ya nje, na uso wa nje wa shell ya nje?

Kielelezo kinaonyesha sehemu ya shells mbili za mviringo. Ya ndani ina radius R1 na moja ya nje ina radius R2.

90. Malipo ya uhakika ya Q=5.0×10—8cq=5.0×10—8C huwekwa katikati ya shell isiyosafishwa ya mviringo ya radius ya ndani 6.0 cm na radius ya nje 9.0 cm. Pata shamba la umeme kwenye (a) r=4.0cmr = 4.0cm, (b) r=8.0cmr = 8.0cm, na (c) r=12.0cmr = 12.0cm. (d) Ni mashtaka gani yanayotokana na nyuso za ndani na nje za shell?

Changamoto Matatizo

91. Darubini ya Hubble Space inaweza kupima mtiririko wa nishati kutoka vitu vya mbali kama vile supernovae na nyota. Wanasayansi basi hutumia data hii kuhesabu nishati iliyotolewa na kitu hicho. Chagua kitu cha interstellar ambacho wanasayansi wameona kuenea kwa Hubble na (kwa mfano,\(\displaystyle Vega\)) ³, kupata umbali wa kitu hicho na ukubwa wa kioo cha msingi cha Hubble, na uhesabu jumla ya nishati ya nishati. (Kidokezo: Hubble inachukua sehemu ndogo tu ya jumla ya mtiririko.)

92. Rejesha tena sheria ya Gauss kwa uwanja wa mvuto, na\(\displaystyle \vec{g}\) kuelekezwa vyema nje.

93. Karatasi isiyo na sahani ya malipo ya wiani wa malipo ya uso\(\displaystyle σ\) inavyoonyeshwa hapa chini. Shamba la umeme ni umbali gani x kutoka kwenye karatasi? Linganisha matokeo ya hesabu hii na ile ya kazi katika maandiko.

Kielelezo kinaonyesha ndege yenye ishara zaidi juu yake. Inapita kupitia silinda S perpendicularly katikati, kugawanya silinda katika nusu mbili za urefu x kila mmoja. Upeo wa juu wa silinda ni kinachoitwa A. mishale iliyoandikwa E kuibuka kutoka mwisho wote wa silinda, pamoja na mhimili wake.

94. Puto ya mpira wa spherical hubeba malipo ya jumla Swali kusambazwa kwa usawa juu ya uso wake. Katika\(\displaystyle t=0\), radius ya puto ni R. Puto ni kisha umechangiwa polepole mpaka radius yake ifikia 2R wakati huo\(\displaystyle t_0\). Kuamua uwanja wa umeme kutokana na malipo haya kama kazi ya wakati

(a) juu ya uso wa puto,

(b) kwenye uso wa radius R, na

(c) kwenye uso wa radius 2R. Puuza athari yoyote kwenye uwanja wa umeme kutokana na vifaa vya puto na kudhani kuwa radius huongezeka kwa usawa na wakati.

95. Pata shamba la umeme la sahani kubwa ya uendeshaji iliyo na malipo ya wavu q. Hebu A kuwa eneo la upande mmoja wa sahani na h unene wa sahani (angalia hapa chini). Malipo kwenye sahani ya chuma yatasambaza zaidi kwenye pande mbili za mipango na kidogo sana kwenye kando ikiwa sahani ni nyembamba.

Wachangiaji na Majina

Template:ContribOpenStaxUni