8.3: Orbital Magnetic Dipole Moment ya Electron

Last updated
Save as PDF

Page ID: 175578

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Eleza kwa nini atomi ya hidrojeni ina mali magnetic
Eleza kwa nini viwango vya nishati vya atomi ya hidrojeni vinavyohusishwa na kasi ya angular ya orbital vinagawanyika na shamba la nje la magnetic
Tumia namba za quantum kuhesabu ukubwa na mwelekeo wa wakati wa dipole ya magnetic ya orbital ya atomi ya hidrojeni.

Katika mfano wa Bohr wa atomi ya hidrojeni elektroni huenda katika obiti ya mviringo kuzunguka protoni. Electron hupita kwa hatua fulani juu ya kitanzi kwa wakati fulani, hivyo tunaweza kuhesabu sasa\(I = Q/t\). Electron ambayo inazunguka protoni katika atomi ya hidrojeni kwa hiyo ni sawa na sasa inapita kupitia waya mviringo (Kielelezo\(\PageIndex{1}\)). Katika utafiti wa magnetism, tuliona kwamba waya wa sasa wa kubeba hutoa mashamba ya magnetic. Kwa hiyo ni busara kuhitimisha kwamba atomi ya hidrojeni inazalisha shamba la magnetic na inaingiliana na mashamba mengine ya magnetic.

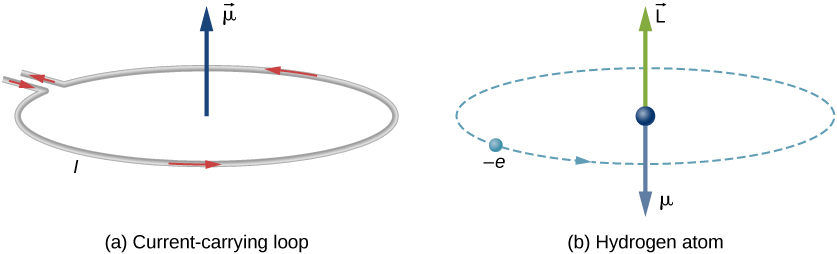
Kielelezo (a) kinaonyesha kitanzi cha sasa cha kubeba. kitanzi ina sasa mimi zinazozunguka kinyume chake kama kutazamwa kutoka juu. Vector mu akizungumzia juu inavyoonekana katikati ya kitanzi. Kielelezo (b) inaonyesha atomi ya hidrojeni kama elektroni, iliyowakilishwa kama mpira mdogo na kinachoitwa bala e, na kufanya mzunguko wa mviringo kinyume, kama inavyotazamwa kutoka hapo juu. Tufe, vector mu akizungumzia chini, na vector L inayoelekeza juu inavyoonekana katikati ya obiti. — Kielelezo\(\PageIndex{1}\): (a) Sasa inapita kupitia waya mviringo ni sawa na (b) elektroni inayozunguka protoni katika atomi ya hidrojeni.

Wakati wa magnetic dipole ya orbital ni kipimo cha nguvu ya shamba la magnetic zinazozalishwa na kasi ya angular ya orbital ya elektroni. Kutoka Nguvu na Torque juu ya Loop ya Sasa, ukubwa wa muda wa magnetic dipole ya orbital kwa kitanzi cha sasa ni

\[\mu = IA, \nonumber \]

wapi\(I\) sasa na\(A\) ni eneo la kitanzi. (Kwa ufupi, tunataja hii kama wakati wa magnetic.) Sasa\(I\) inayohusishwa na elektroni katika obiti kuhusu protoni katika atomi ya hidrojeni ni

\[I = \dfrac{e}{T}, \label{eq1} \]

ambapo e ni ukubwa wa malipo ya elektroni na\(T\) ni kipindi chake cha orbital. Ikiwa tunadhani kwamba elektroni husafiri katika obiti kamili ya mviringo, kipindi cha orbital ni

\[T = \dfrac{2\pi r}{v}, \nonumber \]

ambapo r ni radius ya obiti na v ni kasi ya elektroni katika obiti yake. Kutokana na kwamba eneo la mduara ni\(\pi r^2\), wakati wa magnetic kabisa ni

\[\mu = IA = \dfrac{e}{\left(\dfrac{2\pi r}{v}\right)}\pi r^2 = \dfrac{evr}{2}. \nonumber \]

Ni muhimu kueleza kasi ya magnetic μμ kwa suala la kasi ya angular ya orbital (\(\vec{L} = \vec{r} \times \vec{p}\)). Kwa sababu mzunguko wa elektroni kwenye mduara, vector ya msimamo\(\vec{r}\) na vector\(\vec{p}\) ya kasi huunda pembe sahihi. Hivyo, ukubwa wa kasi ya angular ya orbital ni

\[L = |\vec{L}| = |\vec{r} \times \vec{p}| = rp \, \sin \, \theta = rmv. \label{eq2} \]

Kuchanganya equations hizi mbili, tuna

\[\mu = \left(\dfrac{e}{2m_e}\right)L. \label{eq3} \]

Katika fomu kamili ya vector, maneno haya yameandikwa kama

\[\vec{\mu} = - \left(\dfrac{e}{2m_e}\right)\vec{L}. \label{BIG} \]

Ishara hasi inaonekana kwa sababu elektroni ina malipo hasi. Angalia kwamba mwelekeo wa wakati wa magnetic wa elektroni ni antiparallel kwa kasi ya angular ya orbital, kama inavyoonekana katika Kielelezo\(\PageIndex{1b}\). Katika mfano wa Bohr wa atomi, uhusiano kati\(\vec{\mu}\) na\(\vec{L}\) katika Equation\ ref {BIG} ni huru ya radius ya obiti.

Wakati wa magnetic pia\(μ\) unaweza kuelezwa kwa mujibu wa namba ya angular ya angular quantum\(l\). Kuchanganya Equation\ ref {eq2} na Equation\ ref {eq1}, ukubwa wa wakati wa magnetic ni

\[\mu = \left(\dfrac{e}{2m_e}\right)L = \left(\dfrac{e}{2m_e} \right) \sqrt{l(l + 1)}\hbar = \mu_B \sqrt{l(l + 1)}. \label{eq5} \]

Sehemu ya z ya wakati wa magnetic ni

\[ \begin{align} \mu_z &= -\left(\dfrac{e}{2m_e}\right) \, L_z \\[4pt] &= - \left(\dfrac{e}{2m_e}\right) \, m \hbar \\[4pt] &= - \mu_B m. \label{eq6} \end{align} \]

Kiasi\(\mu_B\) ni kitengo cha msingi cha sumaku kinachoitwa magneton ya Bohr, ambayo ina thamani\(9.3 \times 10^{-24} \, Joule/Tesla\) (J/T) au\(5.8 \times 10^{-5} eV/T\). Quantization ya wakati magnetic ni matokeo ya quantization ya kasi orbital angular.

Kama tutakavyoona katika sehemu inayofuata, wakati wa jumla wa magnetic dipole wa atomi ya hidrojeni ni kutokana na mwendo wa orbital wa elektroni na spin yake ya ndani. Kwa sasa, tunapuuza athari za spin ya elektroni.

Mfano\(\PageIndex{1}\): Orbital Magnetic Dipole Moment

Je! Ni ukubwa gani wa wakati wa magnetic ya dipole ya orbital μ ya elektroni katika atomi ya hidrojeni katika hali ya (a) s, (b) p, na (c) d hali? (Fikiria kwamba spin ya elektroni ni sifuri.)

Mkakati

Kasi ya magnetic ya elektroni inahusiana na kasi yake ya angular ya orbital L. Kwa atomi ya hidrojeni, kiasi hiki kinahusiana na namba ya angular ya angular ya orbital l. Mataifa hutolewa kwa notation spectroscopic, ambayo inahusiana na barua (s, p, d, nk) kwa idadi ya quantum.

Suluhisho

Ukubwa wa wakati wa magnetic hutolewa katika Equation\ ref {eq5}:

\[ \begin{align} \mu_z &= -\left(\dfrac{e}{2m_e}\right) \, L \nonumber \\[4pt] &= \left(\dfrac{e}{2m_e}\right) \, \sqrt{l(l + 1)} \hbar \nonumber \\[4pt] &= \mu_B\sqrt{l(l + 1)}. \end{align} \nonumber \]

Kwa hali s,\(l = 0\) hivyo tuna\(\mu = 0\) na\(\mu_z = 0\).
Kwa hali p,\(l = 0\) na tuna\[\mu = \mu_B\sqrt{1(1 + 1)} = \sqrt{2}\mu_B \nonumber \]\[\mu_z = -\mu_Bm \nonumber \] ambapo\(m = (-1, 0, 1)\) hivyo\[\mu_z = \mu_B, \, 0, \, -\mu_B. \nonumber \]
Kwa hali d,\(l = 2\) na sisi kupata\[\mu = \mu_B\sqrt{2(2 + 1)} = \sqrt{6}\mu_B \nonumber \]\[\mu_z = -\mu_Bm \nonumber \] ambapo\(m = (-2, -1, 0, 1, 2)\)\[\mu_z = 2\mu_B, \, \mu_B \, 0, \, -\mu_B \, -2\mu_B. \nonumber \]

Umuhimu

Katika hali ya s, hakuna kasi ya angular ya orbital na kwa hiyo hakuna wakati wa magnetic. Hii haimaanishi kwamba elektroni inapumzika, tu kwamba mwendo wa jumla wa elektroni hauzalishi shamba la magnetic. Katika hali ya p, elektroni ina wakati wa magnetic na maadili matatu iwezekanavyo kwa sehemu ya z ya wakati huu wa magnetic; hii ina maana kwamba wakati wa magnetic unaweza kuelezea katika maelekezo matatu tofauti ya polar - kila antiparallel kwa vector orbital angular kasi. Katika hali ya d, elektroni ina muda wa magnetic na maadili tano iwezekanavyo kwa z -sehemu ya wakati huu wa magnetic. Katika kesi hii, wakati wa magnetic unaweza kuelezea maelekezo tano tofauti ya polar.

Atomu ya hidrojeni ina shamba la sumaku, hivyo tunatarajia atomu ya hidrojeni kuingiliana na shamba la nje la magnetiki—kama vile kushinikiza na kuvuta kati ya sumaku mbili za bar Kutoka Nguvu na Torque kwenye Loop ya Sasa, tunajua kwamba wakati kitanzi cha sasa kinapoingiliana na shamba la nje la magnetic\(\vec{B}\), linapata wakati uliotolewa na

\[\vec{\tau} = I(\vec{A} \times \vec{B}) = \vec{\mu} \times \vec{B}, \nonumber \]

ambapo mimi ni sasa,\(\vec{A}\) ni eneo la kitanzi, ni wakati wa magnetic, na\(\vec{B}\) ni shamba la nje la magnetic.\(\vec{\mu}\) Wakati huu hufanya mzunguko wa vector ya wakati wa magnetic ya atomi ya hidrojeni ili kuunganisha na shamba la nje la magnetic. Kwa sababu kazi ya mitambo inafanywa na shamba la nje la magnetic kwenye atomu ya hidrojeni, tunaweza kuzungumza juu ya mabadiliko ya nishati katika atomu. Nishati ya uwezo wa atomi ya hidrojeni inayohusishwa na mwingiliano huu wa magnetic inatolewa na Equation\ ref {eq30}:

\[U = -\vec{\mu} \cdot \vec{B}. \label{eq30} \]

Ikiwa wakati wa magnetic ni kinyume na shamba la nje la magnetic, nishati ya uwezo ni kubwa, lakini ikiwa wakati wa magnetic ni sawa na shamba, nishati ya uwezo ni ndogo. Kazi iliyofanywa kwenye atomi ya hidrojeni ili kugeuza vector ya wakati wa magnetic ya atomi katika mwelekeo wa shamba la nje la magnetic kwa hiyo inahusishwa na kushuka kwa nishati ya uwezo. Nishati ya mfumo huhifadhiwa, hata hivyo, kwa sababu kushuka kwa nishati inayozalisha mionzi (chafu ya photon). Mabadiliko haya ya nishati yanathibitishwa kwa sababu wakati wa magnetic unaweza kuelekeza kwa njia fulani tu.

Ikiwa uwanja wa nje wa magnetic unasema katika mwelekeo mzuri wa z, nishati inayohusishwa na wakati wa magnetic wa dipole ya orbital ni

\[U(\theta) = -\mu B \, cos \, \theta = - \mu_z B = - (-\mu_B m) = m\mu_BB, \nonumber \]

wapi\(\mu_B\) magneton ya Bohr na m ni makadirio ya kasi ya angular nambari ya quantum (au idadi ya magnetic orbital quantum), ambayo ina maadili

\[m = -l, -l + 1, ..., 0, ..., l - 1, l. \nonumber \]

Kwa mfano, katika hali ya\(l = 1\) elektroni, nishati ya jumla ya elektroni imegawanyika katika viwango vitatu tofauti vya nishati vinavyolingana na\(U = -\mu_B B, 0, \mu_B B\).

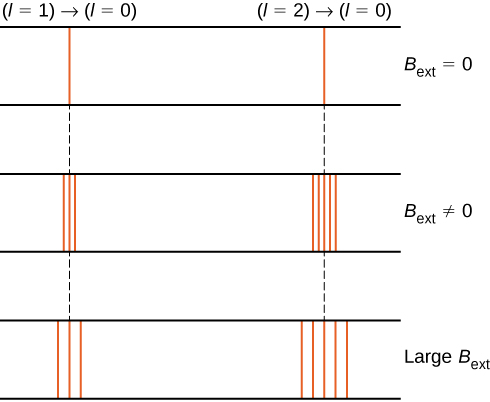
Takwimu inaonyesha athari za shamba la magnetic, B ndogo ext, kwenye mistari miwili tofauti ya spectral, sambamba na mpito wa l = 1 hadi l = 0 upande wa kushoto na mpito wa l = 2 hadi l = 0 upande wa kulia. Spectra huonyeshwa kwa shamba lolote la nje, kwa shamba lisilo la nje la sifuri na kwa shamba kubwa la nje. Kwa shamba lolote la nje, mabadiliko yote yanaonekana kama mistari moja. Katika kesi ya pili, wakati shamba la magnetic linatumiwa, mistari ya spectral imegawanyika katika mistari kadhaa; mstari upande wa kushoto umegawanyika katika mistari mitatu. Mstari juu ya haki hugawanyika katika tano. Katika kesi ya tatu, shamba la magnetic ni kubwa. Mstari wa kushoto umegawanyika tena katika mistari mitatu na haki ndani ya tano, lakini mistari ya kupasuliwa ni mbali zaidi kuliko ilivyo wakati shamba la nje la magnetic sio nguvu. — Kielelezo\(\PageIndex{2}\): Athari ya Zeeman inahusu kugawanyika kwa mistari ya spectral na shamba la nje la magnetic. Katika safu ya kushoto, kugawanyika kwa nishati hutokea kutokana na mabadiliko kutoka kwa hali (\(n = 2, \, l = 1\)) hadi hali ya chini ya nishati; na katika safu ya haki, kugawanyika kwa nishati hutokea kutokana na mabadiliko kutoka hali (\(n = 2, \, l = 2\)) hadi hali ya chini ya nishati. Kugawanyika kwa mistari hii ni sawa na nguvu ya shamba la nje la magnetic.

Kugawanyika kwa viwango vya nishati na uwanja wa nje wa magnetic huitwa athari ya Zeeman. Kupuuza madhara ya spin ya elektroni, mabadiliko kutoka\(l = 1\) hali hadi hali ya kawaida ya nishati huzalisha mistari mitatu ya spectral karibu (Kielelezo\(\PageIndex{2}\), safu ya kushoto). Vivyo hivyo, mabadiliko kutoka kwa\(l = 2\) serikali yanazalisha mistari mitano ya spectral karibu (safu ya kulia). Kugawanyika kwa mistari hii ni sawa na nguvu ya shamba la nje la magnetic. Athari hii ina programu nyingi. Kwa mfano, kugawanyika kwa mistari katika wigo wa hidrojeni wa Jua hutumiwa kuamua nguvu ya uwanja wa magnetic wa Jua. Vipimo vingi vya magnetic shamba vinaweza kutumika kutengeneza ramani ya shughuli za magnetic kwenye uso wa Sun inayoitwa magnetogram (Kielelezo\(\PageIndex{3}\)).

Magnetogram ya jua, ambayo inaonekana kama disc kijivu dhidi ya background nyeusi, na matangazo nyeupe na nyeusi waliotawanyika juu yake. Wengi wa matangazo ni kujilimbikizia katika sehemu ya katikati ya haki ya picha. — Kielelezo\(\PageIndex{3}\): Magnetogram ya Jua. Matangazo mkali na giza yanaonyesha shughuli muhimu za magnetic kwenye uso wa Jua.