8.2: Atom ya hidrojeni
- Page ID
- 175677
Mwishoni mwa sehemu hii, utaweza:
- Eleza atomi ya hidrojeni kwa suala la kazi ya wimbi, wiani wa uwezekano, nishati ya jumla, na kasi ya angular ya orbital
- Tambua umuhimu wa kimwili wa kila namba za quantum (n, l, m) ya atomi ya hidrojeni
- Tofautisha kati ya mifano ya Bohr na Schrödinger ya atomi
- Tumia namba za quantum kuhesabu habari muhimu kuhusu atomi ya hidrojeni
Atomi ya hidrojeni ni atomi rahisi katika asili na, kwa hiyo, mwanzo mzuri wa kujifunza atomi na muundo wa atomiki. Atomu ya hidrojeni ina elektroni moja yenye kushtakiwa vibaya inayozunguka protoni yenye kushtakiwa vyema (Kielelezo\(\PageIndex{1}\)). Katika mfano wa Bohr, elektroni hutolewa karibu na protoni katika obiti ya mviringo kikamilifu na nguvu ya kuvutia ya Coulomb. Protoni ni takriban mara 1800 kubwa kuliko elektroni, hivyo protoni huenda kidogo sana katika kukabiliana na nguvu juu ya protoni kwa elektroni. (Hii ni sawa na mfumo wa Dunia-Sun, ambapo Jua huenda kidogo sana kwa kukabiliana na nguvu inayotumiwa na Dunia.) Maelezo ya athari hii kwa kutumia sheria za Newton hutolewa katika Photons na Matter Waves.
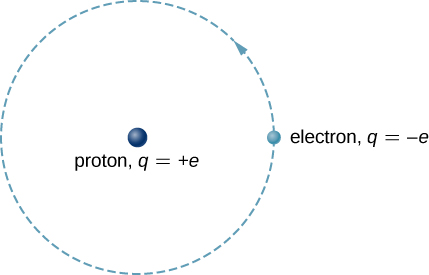
Kwa dhana ya proton iliyowekwa, tunazingatia mwendo wa elektroni.
Katika uwanja wa umeme wa proton, nishati ya uwezo wa elektroni ni
\[U(r) = -k\frac{e^2}{r}, \nonumber \]
wapi\(k = 1/4\pi\epsilon_0\) na\(r\) ni umbali kati ya elektroni na protoni. Kama tulivyoona mapema, nguvu juu ya kitu ni sawa na hasi ya gradient (au mteremko) wa kazi ya uwezo wa nishati. Kwa kesi maalum ya atomi ya hidrojeni, nguvu kati ya elektroni na proton ni nguvu ya kuvutia ya Coulomb.
Angalia kwamba kazi ya nishati ya uwezo\(U(r)\) haina kutofautiana kwa wakati. Matokeo yake, equation ya Schrödinger ya atomi ya hidrojeni inapunguza kwa equations mbili rahisi: moja ambayo inategemea tu nafasi (x, y, z) na nyingine ambayo inategemea tu wakati (t). (mgawanyo wa kazi wimbi katika nafasi- na sehemu wakati-tegemezi kwa muda wa kujitegemea kazi uwezo nishati ni kujadiliwa katika Quantum Mechanics.) Sisi ni zaidi nia ya equation nafasi-tegemezi:
\[\frac{-\hbar}{2m_e}\left(\frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2}\right) - k\frac{e^2}{r}\psi = E\psi, \nonumber \]
\(\psi = psi (x,y,z)\)wapi wimbi tatu-dimensional kazi ya elektroni, meme ni wingi wa elektroni, na\(E\) ni nishati ya jumla ya elektroni. Kumbuka kwamba kazi ya wimbi la jumla\(\Psi (x,y,z,t)\), ni bidhaa ya kazi ya wimbi la kutegemea nafasi\(\psi = \psi(x,y,z)\) na kazi ya wimbi la muda\(\varphi = \varphi(t)\).
Mbali na kuwa muda wa kujitegemea, pia\(U(r)\) ni spherically symmetrical. Hii inaonyesha kwamba tunaweza kutatua equation Schrödinger kwa urahisi zaidi kama sisi kueleza katika suala la kuratibu spherical (\(r, \theta, \phi\)) badala ya kuratibu mstatili (\(x,y,z\)). Mfumo wa kuratibu wa spherical unaonyeshwa kwenye Kielelezo\(\PageIndex{2}\). Katika viwianishi vya spherical, kutofautiana\(r\) ni kuratibu radial,\(\theta\) ni angle ya polar (kuhusiana na wima z -axis), na\(\phi\) ni angle azimuthal (kuhusiana na x -axis). Uhusiano kati ya kuratibu za mviringo na mstatili ni\(x = r \, \sin \, \theta \, \cos \, \phi\),\(y = r \, \sin \theta \, \sin \, \phi\),\(z = r \, \cos \, \theta\).
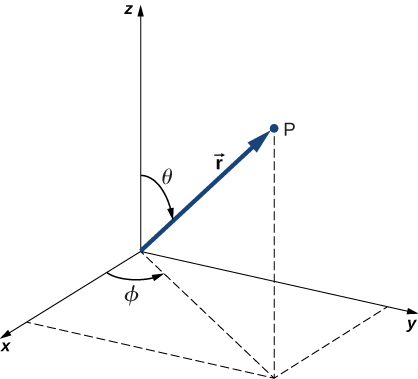
Sababu\(r \, \sin \, \theta\) ni ukubwa wa vector iliyoundwa na makadirio ya vector polar kwenye xy -plane. Pia, kuratibu za x na y zinapatikana kwa kuashiria vector hii kwenye x - na y -axes, kwa mtiririko huo. Mabadiliko ya inverse hutoa
\[\begin{align*} r &= \sqrt{x^2 + y^2 + z^2} \\[4pt] \theta &= \cos^{-1} \left(\frac{z}{r}\right), \\[4pt] \phi &= \cos^{-1} \left( \frac{x}{\sqrt{x^2 + y^2}}\right) \end{align*} \nonumber \]
Schrödinger ya wimbi equation kwa atomi hidrojeni katika kuratibu spherical ni kujadiliwa katika kozi ya juu zaidi katika fizikia ya kisasa, hivyo sisi si kufikiria kwa undani hapa. Hata hivyo, kutokana na ulinganifu spherical ya\(U(r)\), equation hii inapunguza kwa milinganyo tatu rahisi: moja kwa kila moja ya kuratibu tatu (\(r\)\(θ\),, na\(ϕ\)). Ufumbuzi wa kazi ya wimbi la kujitegemea wakati umeandikwa kama bidhaa ya kazi tatu:
\[\psi (r, \theta, \phi) = R(r) \Theta(\theta) \Phi (\phi), \nonumber \]
wapi\(R\) kazi ya radial inategemea kuratibu radial\(r\) tu;\(Θ\) ni kazi ya polar inategemea kuratibu polar\(θ\) tu; na\(Φ\) ni kazi ya phi\(ϕ\) tu. Ufumbuzi halali wa equation Schrödinger\(ψ(r, θ, ϕ)\) ni kinachoitwa na idadi quantum\(n\)\(l\),, na\(m\).
- \(n\): nambari kuu ya quantum
- \(l\): angular kasi quantum idadi
- \(m\): angular kasi makadirio quantum idadi
(Sababu za majina haya zitaelezewa katika sehemu inayofuata.) Kazi ya radial\(R\) inategemea tu\(n\) na\(l\); kazi ya polar\(\Theta\) inategemea tu\(l\) na\(m\); na kazi ya phi\(\Phi\) inategemea tu\(m\). Utegemezi wa kila kazi kwenye namba za quantum unaonyeshwa kwa usajili:
\[\psi_{nlm}(r, \theta, \phi) = R_{nl}(r)\Theta_{lm}(\theta)\Phi_m(\phi). \nonumber \]
Sio seti zote za namba za quantum (\(n\)\(l\),,\(m\)) zinawezekana. Kwa mfano, nambari ya quantum ya angular ya orbital\(l\) haiwezi kamwe kuwa kubwa au sawa na idadi kuu ya quantum\(n(l < n)\). Hasa, tuna
- \(n = 1,2,3,...\)
- \(l = 0,1,2,...,(n-1)\)
- \(m = -l, (-l+1), . . ., 0, . . ., (+l - 1), +l\)
Kumbuka kwamba kwa hali ya ardhi,\(n = 1\),\(l = 0\), na\(m = 0\). Kwa maneno mengine, kuna moja tu quantum hali na kazi wimbi kwa\(n = 1\), na ni\(\psi_{100}\). Hata hivyo, kwa\(n = 2\), tuna
\[l = 0, \, m = 0 \nonumber \]
na
\[l = 1, \, m = -1, 0, 1. \nonumber \]
Kwa hiyo, majimbo ya kuruhusiwa kwa\(n = 2\) serikali ni\(\psi_{200}\),\(\psi_{21-1}\),\(\psi_{210}\), na\(\psi_{211}\). Mfano kazi wimbi kwa atomi hidrojeni ni kutolewa katika Jedwali\(\PageIndex{1}\). Kumbuka kwamba baadhi ya maneno haya yana barua\(i\), ambayo inawakilisha\(\sqrt{-1}\). Wakati probabilities ni mahesabu, namba hizi ngumu hazionekani katika jibu la mwisho.
| \(n = 1, \, l = 0, \, m_l = 0\) | \(\displaystyle \psi_{100} = \frac{1}{\sqrt{\pi}} \frac{1}{a_0^{3/2}}e^{-r/a_0}\) |
| \(n = 2, \, l = 0, \, m_l = 0\) | \(\displaystyle\psi_{200} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}(2 - \frac{r}{a_0})e^{-r/2a_0}\) |
| \(n = 2, \, l = 1, \, m_l = -1\) | \(\displaystyle\psi_{21-1} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{-i\phi}\) |
| \(n = 2, \, l = 1, \, m_l = 0\) | \( \displaystyle \psi_{210} = \frac{1}{4\sqrt{2\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\cos \, \theta\) |
| \(n = 2, \, l = 1, \, m_l = 1\) | \( \displaystyle\psi_{211} = \frac{1}{8\sqrt{\pi}} \frac{1}{a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}\sin \, \theta e^{i\phi}\) |
Umuhimu wa kimwili wa Hesabu za Quantum
Kila moja ya idadi tatu ya quantum ya atomi ya hidrojeni (\(n\)\(l\),,\(m\)) inahusishwa na kiasi tofauti cha kimwili.
Idadi kuu ya Quantum
Nambari kuu ya quantum\(n\) inahusishwa na nishati ya jumla ya elektroni,\(E_n\). Kwa mujibu wa equation ya Schrödinger:
\[E_n = - \left(\frac{m_ek^2e^4}{2\hbar^2}\right)\left(\frac{1}{n^2}\right) = - E_0 \left(\frac{1}{n^2}\right), \label{8.3} \]
wapi\(E_0 = -13.6 \, eV\). Ona kwamba maneno haya yanafanana na ile ya mfano wa Bohr. Kama ilivyo katika mfano wa Bohr, elektroni katika hali fulani ya nishati haina kung'ara.
Kwa atomi ya hidrojeni, ni ngapi zinazowezekana za quantum zinahusiana na idadi kuu\(n = 3\)? Nguvu za nchi hizi ni nini?
Mkakati
Kwa atomi ya hidrojeni ya nishati iliyotolewa, idadi ya majimbo ya kuruhusiwa inategemea kasi yake ya angular ya orbital. Tunaweza kuhesabu majimbo haya kwa kila thamani ya idadi kuu ya quantum,\(n = 1,2,3\). Hata hivyo, jumla ya nishati inategemea namba kuu ya quantum tu, ambayo ina maana kwamba tunaweza kutumia Equation\ ref {8.3} na idadi ya majimbo kuhesabiwa.
Suluhisho
Ikiwa\(n = 3\), maadili ya kuruhusiwa\(l\) ni 0, 1, na 2. Kama\(l = 0\),\(m = 0\) (1 hali). Kama\(l = 1\),\(m = -1, 0, 1\) (3 majimbo); na kama\(l = 2\),\(m = -2, -1, 0, 1, 2\) (5 majimbo). Kwa jumla, kuna 1 + 3 + 5 = 9 inaruhusiwa majimbo. Kwa sababu nishati jumla inategemea tu juu ya idadi kuu quantum,\(n = 3\), nishati ya kila moja ya majimbo haya ni
\[E_{n3} = -E_0 \left(\frac{1}{n^2}\right) = \frac{-13.6 \, eV}{9} = - 1.51 \, eV. \nonumber \]
Umuhimu
Electroni katika atomi ya hidrojeni inaweza kuchukua majimbo mengi ya kasi ya angular yenye nishati sawa. Kama kasi ya angular ya orbital inavyoongezeka, idadi ya majimbo ya kuruhusiwa yenye ongezeko la nishati sawa.
Angular Moment Orbital Quantum Idadi
Nambari ya angular ya orbital quantum\(l\) inahusishwa na kasi ya angular ya orbital ya elektroni katika atomi ya hidrojeni. Nadharia ya quantum inatuambia kwamba wakati atomi ya hidrojeni iko katika hali\(\psi_{nlm}\), ukubwa wa kasi yake ya orbital angular ni
\[L = \sqrt{l(l + 1)}\hbar, \nonumber \]
wapi\(l = 0, 1, 2, . . . , (n - 1)\).
Matokeo haya ni tofauti kidogo na yale yaliyopatikana kwa nadharia ya Bohr, ambayo inapima kasi ya angular kulingana na utawala\(L = n\), ambapo\(n = 1,2,3, ...\)
Majimbo ya quantum yenye maadili tofauti ya kasi ya angular ya orbital yanajulikana kwa kutumia notation spectroscopic (Jedwali\(\PageIndex{2}\)) Majina s, p, d, na f yanatokana na majaribio ya awali ya kihistoria ya kuainisha mistari ya spectral ya atomiki. (Barua kusimama kwa mkali, mkuu, kueneza, na msingi, kwa mtiririko huo.) Baada ya f, barua zinaendelea kialfabeti.
Hali ya chini ya hidrojeni inateuliwa kama hali ya 1, ambapo “1” inaonyesha kiwango cha nishati (\(n = 1\)) na “s” inaonyesha hali ya kasi ya angular (\(l = 0\)). Wakati\(n = 2\),\(l\) inaweza kuwa ama 0 au 1. The\(n = 2\),\(l = 0\) hali ni mteule “2 s.” The\(n = 2\),\(l = 1\) hali ni mteule “2 p.” Wakati\(n = 3\),\(l\) inaweza kuwa 0, 1, au 2, na majimbo ni 3 s, 3 p, na 3 d, kwa mtiririko huo. Uthibitisho kwa majimbo mengine ya quantum hutolewa katika Jedwali\(\PageIndex{3}\).
| Orbital Quantum Idadi\(l\) | Angular Momentum | Jimbo | Spectroscopic J |
|---|---|---|---|
| \ (l\) "> 0 | 0 | s | Sharp |
| \ (l\) ">1 | \(\sqrt{2}h\) | p | Mkuu |
| \ (l\) "> 2 | \(\sqrt{6}h\) | d | Kueneza |
| \ (l\) ">3 | \(\sqrt{12}h\) | f | Msingi |
| \ (l\) ">4 | \(\sqrt{20}h\) | g | |
| \ (l\) ">5 | \(\sqrt{30}h\) | h |
Nambari ya Quantum ya Kiwango cha
Makadirio ya kasi ya angular nambari ya quantum\(m\) inahusishwa na angle ya azimuthal\(\phi\) (angalia Kielelezo\(\PageIndex{2}\)) na inahusiana na z -sehemu ya kasi ya angular ya orbital ya elektroni katika atomi ya hidrojeni. Sehemu hii inatolewa na
\[L_z = m\hbar, \nonumber \]
wapi\(m = -l, -l + 1, ..., 0, ..., +l - 1, l\).
Sehemu ya z ya kasi ya angular inahusiana na ukubwa wa kasi ya angular na
\[L_z = L \, \cos \theta, \nonumber \]
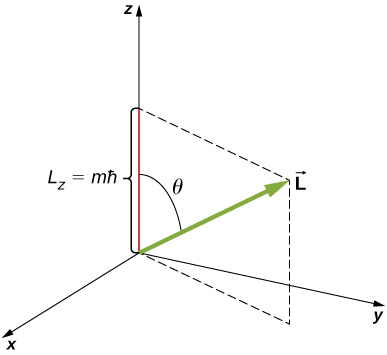
\(\theta\)wapi angle kati ya vector kasi ya angular na z -axis. Kumbuka kuwa mwelekeo wa z -axis imedhamiriwa na jaribio - yaani, pamoja na mwelekeo wowote, jaribio linaamua kupima kasi ya angular. Kwa mfano, mwelekeo wa z unaweza kuendana na mwelekeo wa shamba la nje la magnetic. Uhusiano kati\(L_z\) na\(L\) hutolewa katika Kielelezo\(\PageIndex{3}\).
| \(l = 0\) | \(l = 1\) | \(l = 2\) | \(l = 3\) | \(l = 4\) | \(l = 5\) | |
| \(n = 1\) | 1 s | |||||
| \(n = 2\) | 2 s | 2 p | ||||
| \(n = 3\) | 3 s | 3 p | 3 d | |||
| \(n = 4\) | 4 s | 4 p | 4 d | 4 g | ||
| \(n = 5\) | 5 s | 5 p | 5 d | 50 g | 5 g | |
| \(n = 6\) | 6 s | 6 p | 6 d | 6 g | 6 g | 6 h |
Quantization ya\(L_z\) ni sawa na quantization ya\(\theta\). Kubadilisha\(L\) na\(\sqrt{l(l + 1)}\hbar\)\(m\) kwa\(L_z\) ndani ya equation hii, tunaona
\[m\hbar = \sqrt{l(l + 1)}\hbar \, \cos \, \theta. \nonumber \]
Hivyo, angle\(\theta\) ni quantized na maadili fulani
\[\theta = \cos^{-1}\left(\frac{m}{\sqrt{l(l + 1)}}\right). \nonumber \]
Angalia kwamba angle ya polar (\(θ\)) na makadirio ya vector ya kasi ya angular kwenye z -axis (\(L_z\)) ya kiholela ni quantized.
Quantization ya angle polar kwa\(l = 3\) serikali inavyoonekana katika Kielelezo\(\PageIndex{4}\). Orbital angular kasi vector iko mahali fulani juu ya uso wa koni na angle ya ufunguzi\(\theta\) kuhusiana na z -axis (isipokuwa\(m = 0\), katika kesi ambayo\(θ = 90^o\) na pointi vector ni perpendicular kwa z -axis).
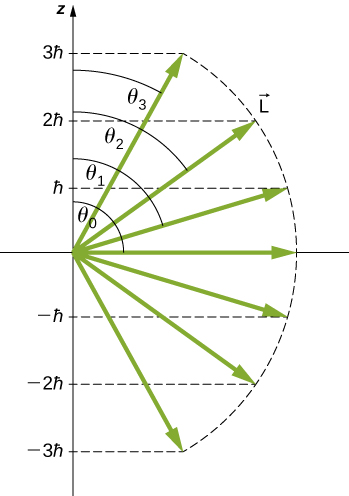
Utafiti wa kina wa kasi ya angular unaonyesha kwamba hatuwezi kujua vipengele vyote vitatu wakati huo huo. Katika sehemu iliyopita, z -sehemu ya kasi ya angular orbital ina maadili ya uhakika ambayo hutegemea idadi ya quantum\(m\). Hii ina maana kwamba hatuwezi kujua wote x- na y -vipengele vya kasi ya angular,\(L_x\) na\(L_y\), kwa uhakika. Matokeo yake, mwelekeo sahihi wa vector ya kasi ya angular ya orbital haijulikani.
Tumia pembe ambazo vector ya kasi ya angular\(\vec{L}\) inaweza kufanya na z -axis kwa\(l = 1\), kama inavyoonekana katika Kielelezo\(\PageIndex{5}\).
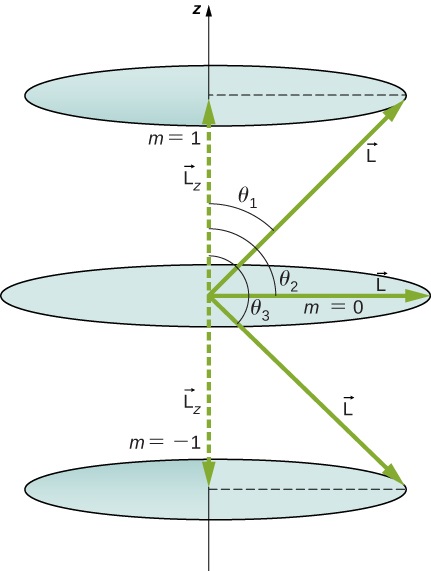
Mkakati
Vectors\(\vec{L}\) na\(\vec{L_z}\) (katika mwelekeo wa z)\(\vec{L}\) huunda pembetatu sahihi, wapi hypotenuse na\(\vec{L_z}\) ni upande wa karibu. Uwiano wa\(L_z\) kwa |\(\vec{L}\) | ni cosine ya angle ya riba. Ukubwa\(L = |\vec{L}|\) na\(L_z\) hutolewa na
\[L = \sqrt{l(l + 1)} \hbar \nonumber \]
na
\[L_z = m\hbar. \nonumber \]
Suluhisho
Tunapewa\(l = 1\), hivyo\(m\) inaweza kuwa +1, 0, au +1. Hivyo,\(L\) ina thamani iliyotolewa na
\[L = \sqrt{l(l + 1)}\hbar = \sqrt{2}\hbar. \nonumber \]
Kiasi\(L_z\) kinaweza kuwa na maadili matatu, iliyotolewa na\(L_z = m_l\hbar\).
\[L_z = \begin{cases} \hbar, & \text{if } m_l=+1 \\ 0, & \text{if } m_l=0 \\ \hbar, & \text{if } m_l=-1 \end{cases} \nonumber \]
Kama unaweza kuona katika Kielelezo\(\PageIndex{5}\)\(\cosθ=Lz/L\), hivyo kwa\(m=+1\), tuna
\[\cos \, \theta_1 = \frac{L_z}{L} = \frac{\hbar}{\sqrt{2}\hbar} = \frac{1}{\sqrt{2}} = 0.707 \nonumber \]
Hivyo,
\[\theta_1 = \cos^{-1}0.707 = 45.0°. \nonumber \]
Vile vile\(m = 0\), kwa, tunaona\(\cos \, \theta_2 = 0\); hii inatoa
\[\theta_2 = \cos^{-1}0 = 90.0°. \nonumber \]
Kisha kwa\(m_l = -1\):
\[\cos \, \theta_3 = \frac{L_Z}{L} = \frac{-\hbar}{\sqrt{2}\hbar} = -\frac{1}{\sqrt{2}} = -0.707, \nonumber \]
ili
\[\theta_3 = \cos^{-1}(-0.707) = 135.0°. \nonumber \]
Umuhimu
Pembe ni sawa na takwimu. Tu angle jamaa na z -axis ni quantized. \(L\)inaweza kuelekeza katika mwelekeo wowote kwa muda mrefu kama inafanya angle sahihi na z -axis. Hivyo, vectors ya kasi ya angular hulala juu ya mbegu, kama ilivyoonyeshwa. Kuona jinsi kanuni ya mawasiliano inashikilia hapa, fikiria kwamba angle ndogo (\(\theta_1\)katika mfano) ni kwa thamani ya juu ya\(m_l\), yaani\(m_l = l\). Kwa kuwa angle ndogo,
\[\cos \, \theta = \dfrac{L_z}{L} = \dfrac{l}{\sqrt{l(l + 1)}}, \nonumber \]
ambayo inakaribia 1 kama\(l\) inakuwa kubwa sana. Ikiwa\(cos \, \theta = 1\), basi\(\theta = 0º\). Zaidi ya hayo\(l\), kwa kubwa, kuna maadili mengi ya\(m_l\), ili pembe zote kuwa inawezekana kama\(l\) anapata kubwa sana.
Je!\(L_z\) Ukubwa unaweza kuwa sawa na\(L\)?
- Jibu
-
Hapana. Nambari ya quantum\(m = -l, -l + l, ..., 0, ..., l -1, l\). Hivyo, ukubwa wa daima\(L_z\) ni chini ya\(L\) kwa sababu\(<\sqrt{l(l + 1)}\)
Kutumia Kazi ya Wave Kufanya Utabiri
Kama tulivyoona mapema, tunaweza kutumia mechanics ya quantum kufanya utabiri kuhusu matukio ya kimwili kwa matumizi ya taarifa za uwezekano. Kwa hiyo ni sahihi kusema, “Electroni iko ndani ya kiasi hiki na uwezekano huu kwa wakati huu,” lakini si, “Electroni iko katika nafasi (x, y, z) kwa wakati huu.” Kuamua uwezekano wa kutafuta elektroni katika atomu ya hidrojeni katika eneo fulani la angani, ni muhimu kuunganisha uwezekano wiani\ (|_ {nlm} |^2) _ juu ya eneo hilo:
\[\text{Probability} = \int_{volume} |\psi_{nlm}|^2 dV, \nonumber \]
\(dV\)wapi kipengele cha kiasi cha infinitesimal. Ikiwa muhimu hii inahesabiwa kwa nafasi zote, matokeo ni 1, kwa sababu uwezekano wa chembe kuwa mahali fulani ni 100% (hali ya kuhalalisha). Katika kozi ya juu zaidi juu ya fizikia ya kisasa, utapata kwamba\(|\psi_{nlm}|^2 = \psi_{nlm}^* \psi_{nlm}\),\(\psi_{nlm}^*\) wapi conjugate tata. Hii inachukua matukio\(i = \sqrt{-1}\) katika hesabu hapo juu.
Fikiria elektroni katika hali ya kasi ya angular ya sifuri (\(l = 0\)). Katika kesi hiyo, kazi ya wimbi la elektroni inategemea tu kuratibu radial\(r\). (Rejea majimbo\(\psi_{100}\) na\(\psi_{200}\) katika Jedwali\(\PageIndex{1}\).) Kipengele cha kiasi cha chini kinafanana na shell ya mviringo ya radius\(r\) na unene wa infinitesimal\(dr\), iliyoandikwa kama
\[dV = 4\pi r^2dr. \nonumber \]
Uwezekano wa kutafuta elektroni katika kanda\(r\) kwa\(r + dr\) (“takriban r”) ni
\[P(r)dr = |\psi_{n00}|^2 4\pi r^2 dr. \nonumber \]
Hapa\(P(r)\) inaitwa radial uwezekano wiani kazi (uwezekano kwa urefu kitengo). Kwa elektroni katika hali ya ardhi ya hidrojeni, uwezekano wa kutafuta elektroni katika eneo\(r\) hilo\(r + dr\) ni
\[|\psi_{n00}|^2 4\pi r^2 dr = (4/a_)^3)r^2 exp(-2r/a_0)dr, \nonumber \]
ambapo\(a_0 = 0.5\) angstroms. Kazi ya wiani ya uwezekano wa radial\(P(r)\) imepangwa kwenye Kielelezo\(\PageIndex{6}\). Eneo chini ya safu kati ya nafasi zozote mbili za radial, sema\(r_1\) na\(r_2\), hutoa uwezekano wa kupata elektroni katika aina hiyo ya radial. Ili kupata nafasi inayowezekana zaidi ya radial, tunaweka derivative ya kwanza ya kazi hii kwa sifuri (\(dP/dr = 0\)) na kutatua\(r\). Msimamo unaowezekana zaidi wa radial si sawa na thamani ya wastani au matarajio ya nafasi ya radial kwa sababu\(|\psi_{n00}|^2\) sio sawa na thamani yake ya kilele.
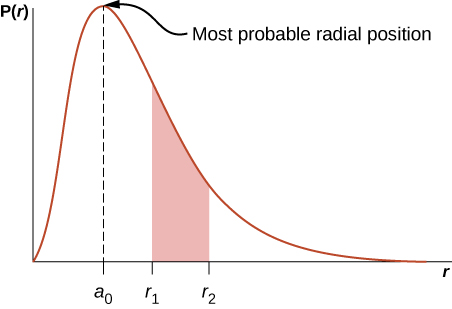
Ikiwa elektroni ina kasi ya angular ya orbital (\(l \neq 0\)), basi kazi za wimbi zinazowakilisha elektroni hutegemea pembe\(\theta\) na\(\phi\); yaani,\(\psi_{nlm} = \psi_{nlm}(r, \theta, \phi)\). Orbitals Atomic kwa majimbo matatu\(n = 2\) na\(l = 1\) ni inavyoonekana katika Kielelezo\(\PageIndex{7}\). Orbital atomia ni kanda katika angani inayozunguka asilimia fulani (kwa kawaida 90%) ya uwezekano wa elektroni. (Wakati mwingine orbitals atomiki hujulikana kama “mawingu” ya uwezekano.) Angalia kwamba mgawanyo huu hutamkwa kwa njia fulani. Mwelekeo huu ni muhimu kwa wanakemia wanapochambua jinsi atomi zinavyofungwa pamoja ili kuunda molekuli.
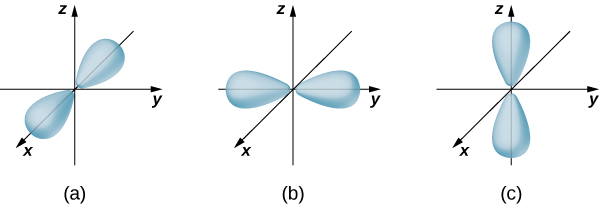
Uwakilishi tofauti kidogo wa kazi ya wimbi hutolewa katika Kielelezo\(\PageIndex{8}\). Katika kesi hiyo, mikoa ya mwanga na giza inaonyesha maeneo ya uwezekano wa juu na mdogo, kwa mtiririko huo. Tofauti na mfano wa Bohr wa atomi ya hidrojeni, elektroni haina kuzunguka kiini cha protoni katika njia iliyoelezwa vizuri. Hakika, kanuni ya kutokuwa na uhakika inafanya kuwa haiwezekani kujua jinsi elektroni inapata kutoka sehemu moja hadi nyingine.