6.6: Mawimbi ya mambo ya De Broglie

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza hypothesis de Broglie ya mawimbi jambo
• Eleza jinsi hypothesis de Broglie inatoa mantiki ya quantization ya kasi angular katika Bohr ya quantum nadharia ya atomi hidrojeni
• Eleza majaribio ya Davisson-Germer
• Tafsiri wazo la de Broglie la mawimbi ya jambo na jinsi wanavyohesabu matukio ya diffraction ya elektroni

Fomu ya Compton ilianzisha kuwa wimbi la sumakuumeme linaweza kuishi kama chembe ya nuru wakati wa kuingiliana na suala. Mwaka 1924, Louis de Broglie alipendekeza nadharia mpya ya kubahatisha kuwa elektroni na chembe nyingine za suala zinaweza kuishi kama mawimbi. Leo, wazo hili linajulikana kama hypothesis de Broglie ya mawimbi ya jambo. Mwaka 1926, hypothesis ya De Broglie, pamoja na nadharia ya awali ya Bohr ya quantum, imesababisha maendeleo ya nadharia mpya ya mechanics ya quantum ya wimbi kuelezea fizikia ya atomi na chembe za subatomiki. Mechanics ya Quantum imetengeneza njia ya uvumbuzi mpya wa uhandisi na teknolojia, kama vile imaging laser na magnetic resonance (MRI). Teknolojia hizi mpya zinaendesha uvumbuzi katika sayansi nyingine kama vile biolojia na kemia.

Kwa mujibu wa hypothesis de Broglie, photons massless pamoja na chembe kubwa lazima kukidhi seti moja ya kawaida ya mahusiano ambayo kuunganisha nishati\(E\) na frequency\(f\), na kasi linear\(p\) na wavelength\(λ\). Tumejadili mahusiano haya kwa photons katika mazingira ya athari za Compton. Tunawakumbusha sasa kwa muktadha wa jumla zaidi. chembe yoyote ambayo ina nishati na kasi ni de Broglie wimbi la mzunguko\(f\) na wavelength\(\lambda\):

\[ E = h f \label{6.53} \]

\[ \lambda = \frac{h}{p} \label{6.54} \]

Hapa,\(E\) na\(p\) ni, kwa mtiririko huo, nishati ya relativistic na kasi ya chembe. Mahusiano ya De Broglie ni kawaida walionyesha katika suala la vector wimbi\(\vec{k}\)\(k = 2 \pi / \lambda\),, na mzunguko wimbi\(\omega = 2 \pi f\), kama sisi kawaida kufanya kwa mawimbi:

\ kuanza {iliyokaa}
&E =\ hbar\ omega\ studio {6.55}\\
&\ vec {p} =\ hbar\ vec {k}\ studio {6.56}
\ mwisho {iliyokaa}

Nadharia ya wimbi inatuambia kwamba wimbi hubeba nishati yake kwa kasi ya kikundi. Kwa mawimbi ya jambo, kasi hii ya kundi ni kasi\(u\) ya chembe. Kutambua nishati E na kasi p ya chembe na nishati yake ya relativistic\(mc^2\) na kasi yake ya relativistic\(mu\), kwa mtiririko huo, inafuata kutoka kwa mahusiano ya Broglie ambayo jambo mawimbi kukidhi uhusiano zifuatazo:

\[ \lambda f =\frac{\omega}{k}=\frac{E / \hbar}{p / \hbar}=\frac{E}{p} = \frac{m c^{2}}{m u}=\frac{c^{2}}{u}=\frac{c}{\beta} \label{6.57} \]

wapi\(\beta = u/c\). Wakati chembe ni massless tuna\(u=c\) na Equation\ ref {6.57} inakuwa\(\lambda f = c\).

Mfano\(\PageIndex{1}\): How Long are de Broglie Matter Waves?

Mahesabu ya de Broglie wavelength ya:

1. mpira wa kikapu 0.65-kg kutupwa kwa kasi ya 10 m/s,
2. elektroni isiyo ya kawaida yenye nishati ya kinetic ya 1.0 eV, na
3. elektroni ya relativistic yenye nishati ya kinetic ya kEV 108.

Mkakati

Tunatumia Equation\ ref {6.57} ili kupata wavelength de Broglie. Wakati tatizo linahusisha kitu cha nonrelativistic kinachohamia kwa kasi ya nonrelativistic u, kama vile katika (a) wakati\(\beta=u / c \ll 1\), tunatumia kasi ya nonrelativistic p. Wakati makadirio nonrelativistic haiwezi kutumika, kama vile katika (c), ni lazima kutumia kasi relativistic\(p=m u=m_{0} \gamma u=E_{0} \gamma \beta/c\), ambapo wengine wingi nishati ya chembe ni\(E_0 = m c^2 \) na\(\gamma\) ni Lorentz sababu\(\gamma=1 / \sqrt{1-\beta^{2}}\). Nishati ya jumla\(E\) ya chembe imetolewa na Equation\ ref {6.53} na nishati ya kinetiki ni\(K=E-E_{0}=(\gamma-1) E_{0}\). Wakati nishati ya kinetic inajulikana, tunaweza Geuza Equation 6.4.2 ili kupata kasi

\[ p=\sqrt{\left(E^{2}-E_{0}^{2}\right) / c^{2}}=\sqrt{K\left(K+2 E_{0}\right)} / c \nonumber \]

na mbadala katika Equation\ ref {6.57} ili kupata

\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}} \label{6.58} \]

Kulingana na tatizo lililopo, katika equation hii tunaweza kutumia maadili yafuatayo kwa hc:

\[ h c=\left(6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)=1.986 \times 10^{-25} \: \mathrm{J} \cdot \mathrm{m}=1.241 \: \mathrm{eV} \cdot \mu \mathrm{m} \nonumber \]

Suluhisho

1. Kwa mpira wa kikapu, nishati ya kinetic ni\[ K=m u^{2} / 2=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})^{2} / 2=32.5 \: \mathrm{J} \nonumber \] na nishati nyingine ya wingi ni\[ E_{0}=m c^{2}=(0.65 \: \mathrm{kg})\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)^{2}=5.84 \times 10^{16} \: \mathrm{J} \nonumber \] Tunaona kwamba\(K /\left(K+E_{0}\right) \ll 1\) na kutumia\(p=m u=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})=6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m} \):\[ \lambda=\frac{h}{p}=\frac{6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}}{6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m}}=1.02 \times 10^{-34} \: \mathrm{m} \nonumber \]
2. Kwa elektroni nonrelativistic,\[ E_{0}=mc^{2}=\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)^{2}=511 \mathrm{keV} \nonumber \] na wakati\(K = 1.0 \: eV\), tuna\(K/(K+E_0) = (1/512) \times 10^{-3} \ll 1\), hivyo tunaweza kutumia formula nonrelativistic. Hata hivyo, ni rahisi hapa kutumia Equation\ ref {6.58}:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{(1.0 \: \mathrm{eV})[1.0 \: \mathrm{eV}+2(511 \: \mathrm{keV})]}}=1.23 \: \mathrm{nm} \nonumber \] Ikiwa tunatumia kasi isiyo ya kawaida, tunapata matokeo sawa kwa sababu 1 eV ni ndogo sana kuliko molekuli iliyobaki ya elektroni.
3. Kwa elektroni ya haraka yenye\(K=108 \: keV\), athari za relativistic haziwezi kupuuzwa kwa sababu nishati yake\(K/E = 108/619\) yote ni\(E = K = E_0 = 108 \: keV + 511 \: keV = 619 \: keV\) na si duni:\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{108 \: \mathrm{keV}[108 \: \mathrm{keV}+2(511 \: \mathrm{keV})]}}=3.55 \: \mathrm{pm} \nonumber \].

Umuhimu

Tunaona kutoka kwa makadirio haya kwamba wavelengths ya De Broglie ya vitu vya macroscopic kama vile mpira ni ndogo sana. Kwa hiyo, hata kama zipo, hazipatikani na haziathiri mwendo wa vitu vya macroscopic.

Zoezi\(\PageIndex{1}\)

Je, ni wavelength ya de Broglie ya proton isiyo ya kawaida yenye nishati ya kinetic ya 1.0 eV?

Jibu

1.7 alasiri

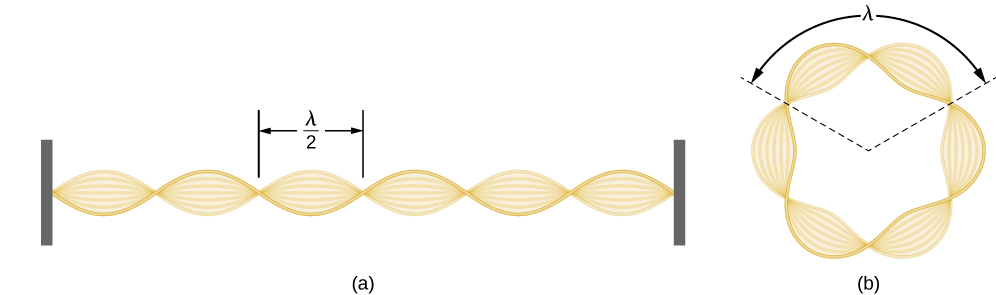
Kutumia dhana ya wimbi la jambo la elektroni, de Broglie ilitoa mantiki ya quantization ya kasi ya angular ya elektroni katika atomi ya hidrojeni, ambayo ilikuwa postulated katika nadharia ya quantum Bohr. Maelezo ya kimwili kwa hali ya kwanza ya upimaji wa Bohr huja kiasili tunapofikiri kwamba elektroni katika atomu ya hidrojeni hutenda si kama chembe bali kama wimbi. Ili kuiona wazi, fikiria kamba ya gitaa iliyotiwa ambayo imefungwa kwa ncha zote mbili na hutetemeka katika mojawapo ya njia zake za kawaida. Ikiwa urefu wa kamba ni l (Kielelezo\(\PageIndex{1}\)), wavelengths ya vibrations hizi haziwezi kuwa kiholela lakini lazima iwe kama idadi ya k ya nusu-wavelengths\(\lambda/2\) inafaa hasa umbali l kati ya mwisho. Hii ni hali\(l=k \lambda /2\) ya wimbi la kusimama kwenye kamba. Sasa tuseme kwamba badala ya kuwa na kamba imefungwa kwenye kuta, tunapiga urefu wake ndani ya mduara na kufunga mwisho wake kwa kila mmoja. Hii inazalisha kamba ya mviringo ambayo hutetemeka kwa njia za kawaida, kukidhi hali sawa ya wimbi la kusimama, lakini idadi ya nusu-wavelengths lazima sasa kuwa idadi hata\(k\)\(k=2n\), na urefu l sasa umeunganishwa na radius\(r_n\) ya mduara. Hii inamaanisha kuwa radii si ya kiholela lakini inapaswa kukidhi hali ya wimbi la kusimama ifuatayo:

\[ 2 \pi r_{n}=2 n \frac{\lambda}{2} \label{6.59}. \]

Ikiwa elektroni katika obiti ya n th Bohr inakwenda kama wimbi, kwa Equation\ ref {6.59} wavelength yake lazima iwe sawa na\(\lambda = 2 \pi r_n / n\). Kutokana kwamba Equation\ ref {6.58} ni halali, wimbi la elektroni la wavelength hii linalingana na kasi ya mstari wa elektroni,\(p = h/\lambda = nh / (2 \pi r_n) = n \hbar /r_n\). Katika obiti ya mviringo, kwa hiyo, kasi ya elektroni ya angular lazima

\[ L_{n}=r_{n} p=r_{n} \frac{n \hbar}{r_{n}}=n \hbar \label{6.60} . \]

Equation hii ni ya kwanza ya hali ya Bohr ya quantization, iliyotolewa na Equation 6.5.6. Kutoa maelezo ya kimwili kwa hali ya upimaji wa Bohr ni hoja inayoshawishi ya kinadharia ya kuwepo kwa mawimbi ya jambo.

Kielelezo\(\PageIndex{1}\): Amesimama-wimbi mfano: (a) kamba aliweka clamped katika kuta; (b) elektroni wimbi trapped katika tatu Bohr obiti katika atomi hidrojeni.

Mfano\(\PageIndex{2}\): The Electron Wave in the Ground State of Hydrogen

Kupata de Broglie wavelength ya elektroni katika hali ya ardhi ya hidrojeni.

Mkakati

Sisi kuchanganya kwanza quantization hali katika Equation\ ref {6.60} na Equation 6.5.6 na kutumia Equation 6.5.9 kwa Radius kwanza Bohr na\(n = 1\).

Suluhisho

Wakati\(n=1\) na\(r_n = a_0 = 0.529 \: Å\), Bohr quantization hali anatoa\(a_{0} p=1 \cdot \hbar \Rightarrow p=\hbar / a_{0}\). Wavelength ya elektroni ni:

\[ \lambda=h / p = h / \hbar / a_{0} = 2 \pi a_{0} = 2 \pi(0.529 \: Å)=3.324 \: Å .\nonumber \]

Umuhimu

Tunapata matokeo sawa tunapotumia Equation\ ref {6.58} moja kwa moja.

Zoezi\(\PageIndex{2}\)

Kupata de Broglie wavelength ya elektroni katika hali ya tatu msisimko wa hidrojeni.

Jibu

\(\lambda = 2 \pi n a_0 = 2 (3.324 \: Å) = 6.648 \: Å\)

Uthibitisho wa majaribio ya mawimbi ya suala ulikuja mwaka wa 1927 wakati C. Davisson na L. Germer walifanya mfululizo wa majaribio ya kutawanyika kwa elektroni ambayo yalionyesha wazi kwamba elektroni hufanya kama mawimbi. Davisson na Germer hawakuanzisha majaribio yao ili kuthibitisha hypothesis de Broglie ya: Uthibitisho ulikuja kama matokeo ya masomo yao ya kawaida ya majaribio ya nyuso za chuma chini ya bombardment ya elektroni.

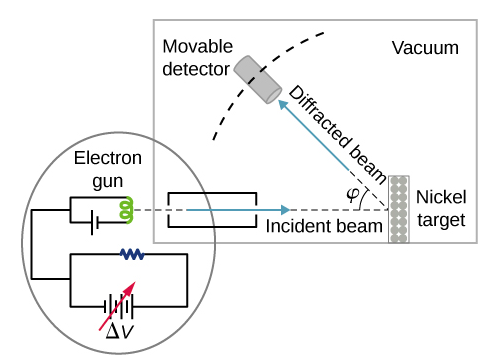
Katika jaribio hasa lililotoa ushahidi wa kwanza kabisa wa mawimbi ya elektroni (inayojulikana leo kama jaribio la Davisson—Germer), walisoma uso wa nikeli. Sampuli yao ya nickel iliandaliwa hasa katika tanuri ya juu-joto ili kubadilisha muundo wake wa kawaida wa polycrystalline kwa fomu ambayo domains kubwa moja ya kioo huchukua kiasi. Kielelezo\(\PageIndex{2}\) inaonyesha kuanzisha majaribio. Electroni za joto hutolewa kutoka elementi yenye joto (kawaida hutengenezwa kwa tungsten) katika bunduki ya elektroni na kuharakisha kupitia tofauti tofauti ΔV, kuwa boriti yenye collimated vizuri ya elektroni zinazozalishwa na bunduki ya elektroni. Nishati\(K\) ya kinetic ya elektroni inarekebishwa kwa kuchagua thamani ya tofauti tofauti katika bunduki ya elektroni. Hii inazalisha boriti ya elektroni yenye thamani ya kuweka ya kasi ya mstari, kwa mujibu wa uhifadhi wa nishati:

\[ e \Delta V=K=\frac{p^{2}}{2 m} \Rightarrow p=\sqrt{2 m e \Delta V} \label{6.61} \]

Boriti ya elektroni ni tukio kwenye sampuli ya nikeli katika mwelekeo wa kawaida kwa uso wake. Juu ya uso, hutawanya kwa njia mbalimbali. Upeo wa boriti uliotawanyika katika mwelekeo uliochaguliwa φφ hupimwa na detector nyeti sana. Msimamo wa angular wa detector kuhusiana na mwelekeo wa boriti ya tukio inaweza kuwa tofauti kutoka φ=0° hadi φ=90°. Kuanzisha nzima imefungwa katika chumba cha utupu ili kuzuia migongano ya elektroni na molekuli za hewa, kama vile migongano ya joto ingebadilisha nishati ya kinetic ya elektroni na haipendekezi.

Kielelezo\(\PageIndex{2}\): Schematics ya kuanzisha majaribio ya majaribio ya Davisson-Germer diffraction majaribio. Boriti yenye collimated ya elektroni imeenea mbali na lengo la nickel. Nishati ya kinetic ya elektroni katika boriti ya tukio huchaguliwa kwa kurekebisha uwezo wa kutofautiana, ΔV, katika bunduki ya elektroni. Upeo wa boriti ya elektroni iliyotawanyika hupimwa kwa pembe mbalimbali za kueneza φ, wakati umbali kati ya detector na lengo haubadilika.

Wakati lengo la nickel lina fomu ya polycrystalline na fuwele nyingi za microscopic zilizoelekezwa kwa nasibu, elektroni za tukio hueneza uso wake kwa njia mbalimbali za random. Matokeo yake, ukubwa wa boriti ya elektroni iliyotawanyika ni sawa katika mwelekeo wowote, unaofanana na kutafakari kwa mwanga kutoka kwenye uso wa porous. Hata hivyo, wakati lengo la nickel lina muundo wa fuwele wa kawaida, ukubwa wa boriti ya elektroni iliyotawanyika inaonyesha upeo wa wazi kwa pembe maalum na matokeo yanaonyesha muundo wa wazi wa diffraction (angalia Mchoro\(\PageIndex{3}\)). Mwelekeo sawa wa diffraction uliotengenezwa na eksirei zilizotawanyika na yabisi mbalimbali za fuwele zilijifunza mwaka 1912 na fizikia wa baba na mwana William H. Bragg na William L. Bragg. Sheria ya Bragg katika crystallography ya X-ray hutoa uhusiano kati\(\lambda\) ya wavelength ya tukio la mionzi kwenye kimiani ya fuwele, nafasi ya kimiani, na nafasi ya kuingiliwa kwa kiwango cha juu katika mionzi iliyotenganishwa (tazama. Diffraction).

Kielelezo\(\PageIndex{3}\): Matokeo ya majaribio ya diffraction ya elektroni kwenye lengo la nickel kwa uwezo wa kuharakisha katika bunduki ya elektroni ya karibu ΔV = 54 V:Upeo wa kiwango cha juu umeandikishwa kwenye angle ya kueneza ya kuhusu φ=50°

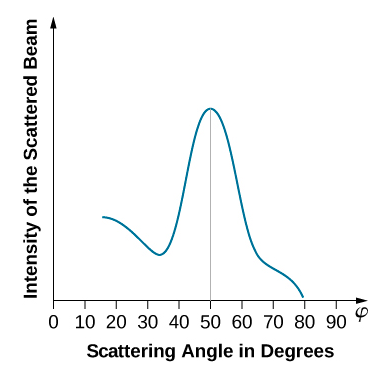
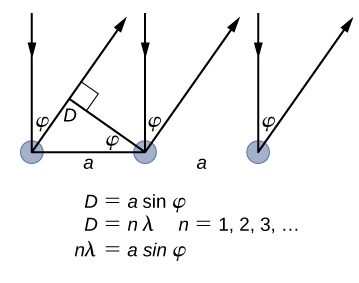
Nafasi ya kimiani ya lengo la Davisson-Germer, iliyowekwa na crystallography ya X-ray, ilipimwa kuwa\(a=2.15 \: Å\). Tofauti na fuwele za X-ray ambazo X-rays hupenya sampuli, katika jaribio la awali la Davisson-Germer, atomi za uso pekee zinaingiliana na boriti ya elektroni ya tukio. Kwa diffraction ya uso, kiwango cha juu cha boriti ya elektroni iliyojitokeza huzingatiwa kwa kueneza pembe ambazo zinakidhi hali nλ = dhambi φ (tazama Mchoro\(\PageIndex{4}\)). Upeo wa kwanza (kwa n=1) hupimwa kwa angle ya kueneza ya φ≈ 50° kwenye ΔV≈ 54 V, ambayo inatoa wavelength ya mionzi ya tukio kama λ= (2.15 Å) dhambi 50° = 1.64 Å. Kwa upande mwingine, uwezo wa 54-V huharakisha elektroni za tukio kwa nguvu za kinetic za K = 54 eV. Kasi yao, iliyohesabiwa kutoka Equation\ ref {6.61}, ni\(p = 2.478 \times 10^{−5} \: eV \cdot s/m\). Wakati sisi badala ya matokeo haya katika Equation\ ref {6.58}, de Broglie wavelength ni kupatikana kama

\[ \lambda=\frac{h}{p}=\frac{4.136 \times 10^{-15} \mathrm{eV} \cdot \mathrm{s}}{2.478 \times 10^{-5} \mathrm{eV} \cdot \mathrm{s} / \mathrm{m}}=1.67 \mathrm{Å} \label{6.62}. \]

Matokeo sawa yanapatikana tunapotumia K = 54eV katika Equation\ ref {6.61}. Ukaribu wa matokeo haya ya kinadharia kwa thamani ya majaribio ya Davisson—Germer ya λ = 1.64 Å ni hoja ya kushawishi kwa kuwepo kwa mawimbi ya jambo la de Broglie.

Kielelezo\(\PageIndex{4}\): Katika diffraction ya uso wa wimbi la umeme la monochromatic kwenye muundo wa tani ya fuwele, mihimili ya tukio la awamu inaonekana kutoka kwa atomi juu ya uso. ray yalijitokeza kutoka atomi kushoto husafiri umbali wa ziada D = dhambi η kwa detector, ambapo ni kimiani nafasi. Mihimili iliyojitokeza inabakia katika awamu wakati D ni integer nyingi ya wavelength yao λ.. Upeo wa mawimbi yaliyojitokeza umetangaza maxima kwa pembe φ kuridhisha nλ = dhambi φ.

Diffraction mistari kipimo na elektroni chini ya nishati, kama vile wale kutumika katika majaribio Davisson-Germer, ni pana kabisa (Kielelezo\(\PageIndex{3}\)) kwa sababu elektroni tukio ni kutawanyika tu kutoka uso. Azimio la picha za diffraction inaboresha sana wakati boriti ya juu ya nishati ya elektroni inapita kupitia foil nyembamba ya chuma. Hii hutokea kwa sababu picha ya diffraction imeundwa kwa kueneza ndege nyingi za fuwele ndani ya kiasi, na maxima zinazozalishwa katika kutawanya kwenye pembe za Bragg ni mkali (Kielelezo\(\PageIndex{5}\)).

Kielelezo\(\PageIndex{5}\): Mwelekeo wa diffraction uliopatikana katika kueneza kwenye imara ya fuwele: (a) na X-rays, na (b) na elektroni. Mfano uliozingatiwa unaonyesha ulinganifu wa muundo wa fuwele wa sampuli.

Tangu kazi ya Davisson na Germer, hypothesis de Broglie imejaribiwa sana na mbinu mbalimbali za majaribio, na kuwepo kwa mawimbi ya de Broglie imethibitishwa kwa chembe nyingi za msingi. Neutroni zimetumika katika kutawanya majaribio kuamua miundo fuwele ya yabisi kutokana na mifumo ya kuingiliwa iliyoundwa na mawimbi ya suala la neutroni. Neutroni ina chaji ya sifuri na masi yake inalinganishwa na masi ya protoni yenye kushtakiwa vyema. Neutroni na protoni zote zinaweza kuonekana kama mawimbi ya jambo. Kwa hiyo, mali ya kuwa wimbi la suala si maalum kwa chembe za kushtakiwa kwa umeme lakini ni kweli ya chembe zote zinazoendelea mwendo. Matter mawimbi ya molekuli kubwa kama kaboni\(C_{60}\) yamepimwa. Vitu vyote vya kimwili, vidogo au vikubwa, vina wimbi la jambo linalohusishwa kwa muda mrefu kama zinabaki katika mwendo. Tabia ya ulimwengu wa mawimbi ya jambo la Broglie imara imara.

Mfano\(\PageIndex{3A}\): Neutron Scattering

Tuseme kwamba boriti ya neutroni hutumiwa katika jaribio la diffraction kwenye imara ya kawaida ya fuwele. Tathmini nishati ya kinetic ya neutroni (katika eV) katika boriti ya neutroni na ulinganishe na nishati ya kinetic ya gesi bora katika usawa kwenye joto la kawaida.

Mkakati

Tunadhani kwamba kawaida kioo nafasi a ni ya utaratibu wa 1.0 Å. Ili kuchunguza muundo wa diffraction kwenye safu hiyo, wavelength ya neutron λ lazima iwe juu ya utaratibu sawa wa ukubwa kama nafasi ya bandia. Tunatumia Equation\ ref {6.61} ili kupata kasi p na kinetic nishati K. Ili kulinganisha nishati hii na nishati\(E_T\) ya gesi bora katika usawa kwenye joto la kawaida\(T = 300 \, K\), tunatumia uhusiano\(K = 3/2 k_BT\), ambapo\(k_B = 8.62 \times 10^{-5}eV/K\) ni mara kwa mara ya Boltzmann.

Suluhisho

Tunatathmini pc ili kulinganisha na nishati ya kupumzika ya neutron\(E_0 = 940 \, MeV\):

\[p = \frac{h}{\lambda} \Rightarrow pc = \frac{hc}{\lambda} = \frac{1.241 \times 10^{-6}eV \cdot m}{10^{-10}m} = 12.41 \, keV. \nonumber \]

Tunaona kwamba\(p^2c^2 << E_0^2\) na tunaweza kutumia nishati nonrelativistic kinetic:

\[K = \frac{p^2}{2m_n} = \frac{h^2}{2\lambda^2 m_n} = \frac{(6.63\times 10^{−34}J \cdot s)^2}{(2\times 10^{−20}m^2)(1.66 \times 10^{−27} kg)} = 1.32 \times 10^{−20} J = 82.7 \, meV. \nonumber \]

Nishati ya kinetic ya gesi bora katika usawa saa 300 K ni:

\[K_T = \frac{3}{2}k_BT = \frac{3}{2} (8.62 \times 10^{-5}eV/K)(300 \, K) = 38.8 \, MeV. \nonumber \]

Tunaona kwamba nguvu hizi ni za utaratibu sawa wa ukubwa.

Umuhimu

Neutrons yenye nguvu katika aina hii, ambayo ni ya kawaida kwa gesi bora kwenye joto la kawaida, huitwa “neutrons ya joto.”

Mfano\(\PageIndex{3B}\): Wavelength of a Relativistic Proton

Katika supercollider katika CERN, protoni zinaweza kuharakishwa kwa kasi ya 0.75 c. Je, ni wavelengths yao ya Broglie kwa kasi hii? Nguvu zao za kinetic ni nini?

Mkakati

Nishati ya molekuli iliyobaki ya proton ni\(E_0 = m_0c^2 = (1.672 \times 10^{−27} kg)(2.998 \times 10^8m/s)^2 = 938 \, MeV\). Wakati kasi ya protoni inajulikana, tuna β = 0.75 na\(\beta \gamma = 0.75 / \sqrt{1 - 0.75^2} = 1.714\). Tunapata wavelength λλ na nishati ya kinetic K kutoka mahusiano ya relativistic.

Suluhisho

\[\lambda = \frac{h}{p} = \frac{hc}{\beta \gamma E_0} = \frac{1.241 \, eV \cdot \mu m}{1.714 (938 \, MeV)} = 0.77 \, fm \nonumber \]

\[K = E_0(\gamma - 1) = 938 \, MeV (1 /\sqrt{1 - 0.75^2} - 1) = 480.1\, MeV \nonumber \]

Umuhimu

Kumbuka kwamba kwa sababu protoni ni kubwa zaidi ya mara 1835 kuliko elektroni, ikiwa jaribio hili lilifanyika kwa elektroni, upyaji rahisi wa matokeo haya utatupa wavelength ya elektroni ya (1835) 0.77 fm = 1.4 pm na nishati yake ya kinetic ya 480.1 MeV /1835 = 261.6 kEV.

Zoezi\(\PageIndex{3}\)

Kupata de Broglie wavelength na nishati kinetic ya elektroni bure kwamba safari kwa kasi ya 0.75 c.

Jibu

\(\lambda = 1.417 \, pm; \, K = 261.56 \, keV\)