4.4: Diffraction Mbili-Slit

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Eleza athari ya pamoja ya kuingiliwa na diffraction na slits mbili, kila mmoja na upana wa mwisho
• Kuamua ukubwa wa jamaa wa pindo za kuingiliwa ndani ya muundo wa diffraction
• Kutambua maagizo kukosa, kama ipo

Tuliposoma kuingiliwa katika jaribio la Young la mara mbili, tulipuuza athari ya diffraction katika kila watakata. Tulidhani kwamba slits zilikuwa nyembamba sana kwamba kwenye skrini uliona tu kuingiliwa kwa mwanga kutoka vyanzo viwili tu vya uhakika. Ikiwa mtakata ni mdogo kuliko wavelength, basi Kielelezo 4.3.4a kinaonyesha kwamba kuna tu kuenea kwa mwanga na hakuna kilele au mabwawa kwenye skrini. Kwa hiyo, ilikuwa ni busara kuacha athari ya diffraction katika sura hiyo. Hata hivyo, kama wewe kufanya watakata pana, Kielelezo 4.3.4b na (c) kuonyesha kwamba huwezi kupuuza diffraction. Katika sehemu hii, tunasoma matatizo kwa jaribio la mara mbili linalojitokeza wakati unahitaji pia kuzingatia athari ya diffraction ya kila fungu.

Ili kuhesabu muundo wa diffraction kwa slits mbili (au idadi yoyote ya), tunahitaji kuzalisha njia tuliyotumia tu kwa ajili ya kukata moja. Hiyo ni, katika kila fungu, tunaweka usambazaji sare wa vyanzo vya uhakika ambavyo huangaza mawimbi ya Huygens, na kisha tunahesabu mawimbi kutoka kwenye slits zote. Hii inatoa kiwango wakati wowote kwenye skrini. Ingawa maelezo ya hesabu hiyo yanaweza kuwa ngumu, matokeo ya mwisho ni rahisi sana:

Mfano wa Diffraction Mbili

Mfano wa diffraction wa slits mbili za upana\(a\) ambazo zinajitenga na umbali d ni mfano wa kuingiliwa wa vyanzo viwili vya uhakika vinavyotengwa na d kuongezeka kwa muundo wa diffraction wa upana wa upana\(a\).

Kwa maneno mengine, maeneo ya pindo ya kuingiliwa hutolewa na equation

\[d \, \sin \, \theta = m \lambda \nonumber \]

sawa na tulipozingatia slits kuwa vyanzo vya uhakika, lakini ukubwa wa pindo sasa umepunguzwa na madhara ya diffraction, kulingana na Equation 4.3.11. [Kumbuka kuwa katika sura ya kuingiliwa, tuliandika\(d \, sin \, \theta = m \lambda\) na kutumia integer\(m\) kutaja pindo za kuingiliwa. Equation 4.2.1 pia inatumia\(m\), lakini wakati huu kutaja diffraction minima. Ikiwa equations zote mbili zinatumiwa wakati huo huo, ni mazoea mazuri kutumia variable tofauti (kama vile\(n\)) kwa mojawapo ya integers hizi ili kuziweka tofauti.]

Madhara ya kuingiliwa na diffraction hufanya kazi wakati huo huo na kwa ujumla huzalisha minima kwa pembe tofauti. Hii inasababisha muundo ngumu kwenye skrini, ambapo baadhi ya maxima ya kuingiliwa kutoka slits mbili haipo ikiwa kiwango cha juu cha kuingiliwa ni katika mwelekeo sawa na kiwango cha chini cha diffraction. Tunarejelea kilele cha kukosa kama utaratibu usiopotea. Mfano mmoja wa muundo wa diffraction kwenye skrini umeonyeshwa kwenye Kielelezo\(\PageIndex{1}\). Mstari imara na kilele cha urefu mbalimbali ni kiwango kilichoonekana kwenye skrini. Ni bidhaa ya muundo wa kuingilia kati wa mawimbi kutoka slits tofauti na diffraction ya mawimbi kutoka ndani ya fungu moja.

Kielelezo\(\PageIndex{1}\): Diffraction kutoka kwa kupasuka mara mbili. Mstari wa rangi ya zambarau na kilele cha urefu sawa ni kutokana na kuingiliwa kwa mawimbi kutoka slits mbili; mstari wa bluu na nundu moja kubwa katikati ni diffraction ya mawimbi kutoka ndani ya fungu moja; na mstari mwembamba nyekundu ni bidhaa ya mbili, ambayo ni mfano unaozingatiwa kwenye skrini. njama inaonyesha matokeo inatarajiwa kwa upana watakata\(a = 2\lambda\) na watakata kujitenga\(d = 6\lambda\). Upeo wa\(m = \pm 3\) utaratibu wa kuingiliwa haupo kwa sababu kiwango cha chini cha diffraction hutokea katika mwelekeo huo.

Mfano\(\PageIndex{1}\): Intensity of the Fringes

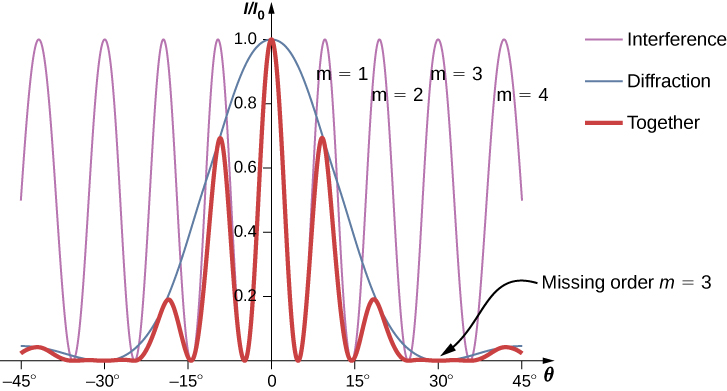
Kielelezo\(\PageIndex{1}\) kinaonyesha kwamba ukubwa wa pindo kwa m=3 ni sifuri, lakini vipi kuhusu pindo nyingine? Tumia kiwango cha pindo saa m=1 kuhusiana na\(I_0\), ukubwa wa kilele cha kati.

Mkakati

Kuamua angle kwa pindo la kuingiliwa mara mbili, kwa kutumia equation kutoka Kuingiliwa, kisha kuamua kiwango cha jamaa katika mwelekeo huo kutokana na diffraction kwa kutumia Equation 4.3.11.

Suluhisho

Kutoka kwenye sura ya kuingiliwa kati, tunajua kwamba pindo za kuingiliwa mkali hutokea\(d \, sin \, \theta = m \lambda\), au

\[\sin \, \theta = \dfrac{m\lambda}{d}. \nonumber \]

Kutoka Equation 4.3.11,

\[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \nonumber \]

wapi

\[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \sin \, \theta}{\lambda}. \nonumber \]

Kubadilisha kutoka hapo juu,

\[\beta = \dfrac{\pi a \sin \, \theta}{\lambda} = \dfrac{\pi a}{\lambda} \cdot \dfrac{m\lambda}{d} = \dfrac{m\pi a}{d}. \nonumber \]

Kwa\(a = 2\lambda, \, d = 6 \lambda\), na\(m = 1\),

\[\beta = \dfrac{(1)\pi (2\lambda)}{(6 \lambda)} = \dfrac{\pi}{3}. \nonumber \]

Kisha, kiwango ni

\[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = I_0 \left(\dfrac{sin \, (\pi/3)}{\pi/3}\right)^2 = 0.684 I_0. \nonumber \]

Umuhimu

Kumbuka kuwa mbinu hii ni kiasi moja kwa moja na inatoa matokeo ambayo ni karibu sawa na uchambuzi ngumu zaidi kwa kutumia phasors kufanya kazi nje ya maadili ya kiwango cha kuingiliwa mara mbili-watakata (nyembamba line katika Kielelezo\(\PageIndex{1}\)). Njia ya phasor akaunti kwa mteremko wa chini katika kiwango cha diffraction (mstari wa bluu) ili kilele karibu na m = 1 hutokea kwa thamani ya milele hivyo kidogo kidogo kuliko tumeonyesha hapa.

Mfano\(\PageIndex{2}\): Two-Slit Diffraction

Tuseme kwamba katika jaribio la Young, slits ya upana 0.020 mm hutenganishwa na 0.20 mm. Ikiwa slits zinaangazwa na mwanga wa monochromatic wa wavelength 500 nm, ngapi pindo za mkali zinazingatiwa katika kilele cha kati cha muundo wa diffraction?

Suluhisho

Kutoka Equation 4.2.1, nafasi ya angular ya kiwango cha chini cha diffraction ni\(\theta \approx sin \, \theta = \dfrac{\lambda}{a} = \dfrac{5.0 \times 10^{-7}m}{2.0 \times 10^{-5}m} = 2.5 \times 10^{-2} rad\).

Kutumia\(d \sin \, \theta = m \lambda\) kwa\(\theta = 2.5 \times 10^{-2} rad\), tunapata

\[m = \dfrac{d \, sin \, \theta}{\lambda} = \dfrac{(0.20 \, mm)(2.5 \times 10^{-2} rad)}{(5.0 \times 10^{-7}m)} = 10, \nonumber \]

ambayo ni kiwango cha juu ili kuingiliwa kwamba inafaa ndani ya kilele cha kati. Tunaona kwamba\(m=±10\) ni kukosa amri kama\(θ\) mechi hasa. Kwa hiyo, tunaona pindo kali

m = -9, -8, -7, -6, -5, -4, -3, -2, -1, 1, +1, +2, +3, +4, +5, +6, +7, +8, na +9

kwa jumla ya 19 pindo mkali.

Zoezi\(\PageIndex{1}\)

Kwa majaribio katika Mfano\(\PageIndex{2}\), onyesha kwamba m=20 pia ni amri ya kukosa.

Suluhisho

Kutoka\(d \, \sin \, \theta = m\lambda\), upeo wa kuingiliwa hutokea\(2.87^o\) kwa\(m = 20\). Kutoka Equation 4.2.1, hii pia ni angle kwa kiwango cha chini cha pili cha diffraction. (Kumbuka: Equations zote mbili hutumia index m lakini zinarejelea matukio tofauti.)

Kuchunguza madhara ya diffraction mbili-watakata. Katika simulation hii iliyoandikwa na Fu-Kwun Hwang, kuchagua N = 2 kutumia slider na kuona nini kinatokea wakati kudhibiti upana watakata, watakata kujitenga na wavelength. Je, unaweza kufanya amri kwenda “kukosa?”