Skip to main content
Global

4.3: Upeo katika Diffraction moja-Slit

  1. Last updated
  2. Save as PDF
  • Page ID
    175347

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tumia jamaa ya kiwango cha juu na upeo wa kati wa kilele cha diffraction moja-slit
    • Tumia kiwango cha jamaa na upeo wa kati wa hatua ya kiholela kwenye skrini

    Ili kuhesabu ukubwa wa muundo wa diffraction, tunafuata njia ya awamu inayotumiwa kwa mahesabu na nyaya za ac katika Mipangilio Mbadala ya Sasa. Kama tunaona kwamba kuna vyanzo\(N\) Huygens katika watakata inavyoonekana hapo awali, na kila chanzo kutengwa na umbali A/n kutoka majirani zake karibu, njia tofauti kati ya mawimbi kutoka vyanzo karibu kufikia hatua holela\(P\) kwenye screen ni\((a/N) \, \sin \theta\). Umbali huu ni sawa na tofauti ya awamu ya\((2\pi a/\lambda N) \, \sin \, \theta\). Mchoro wa phasor kwa mawimbi ya kuwasili kwenye hatua ambayo nafasi ya angular\(\theta\) inavyoonekana kwenye Mchoro\(\PageIndex{1}\). Ukubwa wa phasor kwa kila wavelet ya Huygens ni\(\Delta E_0\), amplitude ya awamu ya matokeo ni\(E\), na tofauti ya awamu kati ya mawimbi kutoka kwa vyanzo vya kwanza na vya mwisho ni

    \[\phi = \left(\dfrac{2\pi}{\lambda}\right) \, a \, \sin \theta. \nonumber \]

    Kwa\(N → ∞\), mchoro wa phasor unakaribia arc ya mviringo ya urefu\(N \Delta E_0\) na radius\(r\). Kwa kuwa urefu wa arc ni\(N \Delta E_0\) kwa chochote\(ϕ\), radius\(r\) ya arc inapaswa kupungua kama\(ϕ\) ongezeko (au sawa, kama phasors huunda spirals kali).

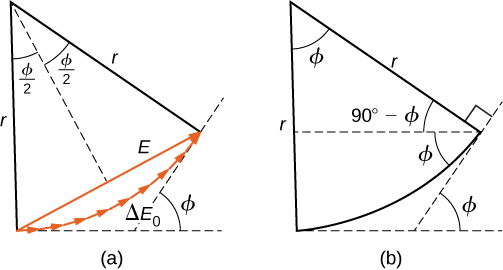
    Kielelezo a inaonyesha safu na phasors kinachoitwa delta E subscript 0. Hii subtends angle katikati ya mduara, kwa njia ya mistari miwili kinachoitwa r. angle hii ni bisected na kila nusu kinachoitwa phi na 2. Mwisho wa arc ni kushikamana na mshale ulioitwa E. tangent katika mwisho mmoja wa arc ni usawa. Tangent katika mwisho mwingine wa arc hufanya phi angle na usawa. Kielelezo b kinaonyesha arc na pembe ya pembe iliyopunguzwa nayo. Mstari wa dotted unatoka kwenye mwisho mmoja wa arc hadi mstari kinyume r. perpendicular kwa r Inafanya phi angle na arc na angle 90 bala phi na mstari wa karibu r.
    Kielelezo\(\PageIndex{1}\): (a) Mchoro wa Phasor unaohusiana na msimamo wa angular katika muundo wa diffraction moja. Tofauti ya awamu kati ya mawimbi kutoka vyanzo vya kwanza na vya mwisho ni\(\phi = (2\pi /\lambda)a \, sin \, \theta\). (b) Jiometri ya mchoro wa phasor.

    Mchoro wa phasor kwa = 0 (katikati ya muundo wa diffraction) umeonyeshwa kwenye Mchoro\(\PageIndex{1a}\) kwa kutumia N=30. Katika kesi hiyo, phasors huwekwa mwisho hadi mwisho wa mstari wa moja kwa moja wa urefu\(N \Delta E_0\), r radius inakwenda kwa infinity, na matokeo yake ina thamani yake ya juu\(E = N\Delta E_0\). Upeo wa mwanga unaweza kupatikana kwa kutumia uhusiano\(I = \dfrac{1}{2} c \epsilon_0 E^2\) kutoka kwa Mawimbi ya umeme. Upeo wa kiwango cha juu ni basi

    \[I_0 = \dfrac{1}{2} c\epsilon_0 (N \Delta E_0)^2 = \dfrac{1}{2\mu_0 c}(N\Delta E_0)^2, \nonumber \]

    wapi\(\epsilon_0 = 1/\mu_0 c^2\). Michoro ya phasor kwa zero mbili za kwanza za muundo wa diffraction zinaonyeshwa kwenye Kielelezo\(\PageIndex{1b}\) na Kielelezo\(\PageIndex{1d}\). Katika hali zote mbili, phasors huongeza sifuri, baada ya kupokezana kupitia\(\phi = 2\pi\) rad kwa m = 1 na\(4 \pi\) rad kwa m = 2.

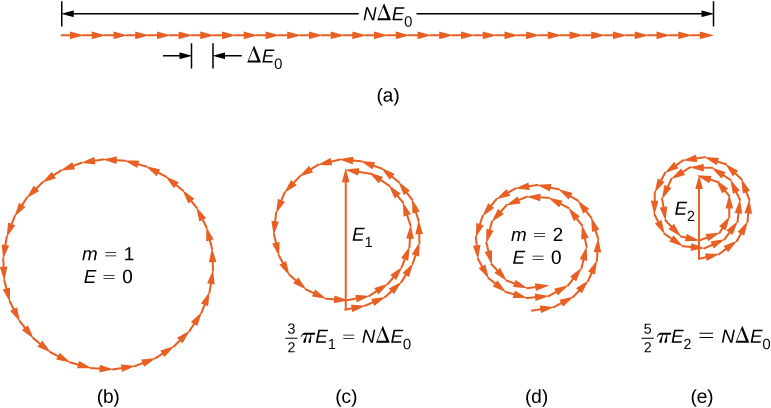
    Kielelezo a inaonyesha 30 phasors katika mstari wa urefu N delta E subscript 0. Urefu wa phasor ni delta E subscript 0. Kielelezo b kinaonyesha mduara na phasors inayoelezea mwelekeo wa anticlockwise. Hii ni labeled m sawa na 1, E sawa na 0. Kielelezo c kinaonyesha awamu kando ya mduara. Wanaanza kutoka chini na kwenda mara moja na nusu karibu na mduara katika mwelekeo wa anticlockwise. Mshale kutoka mwanzo hadi hatua ya mwisho ni kinachoitwa E1. Inaunda kipenyo cha mduara. Kielelezo c kinachoitwa 3 na 2 pi E1 sawa na N delta E0. Kielelezo d inaonyesha awamu kando ya mduara. Wanaanza kutoka chini na kwenda mara mbili karibu na mduara katika mwelekeo wa anticlockwise. Takwimu hiyo imeandikwa m sawa na 2, E sawa na 0. Kielelezo yeye inaonyesha awamu kando ya mduara. Wanaanza kutoka chini na kwenda mara mbili na nusu karibu na mduara katika mwelekeo wa anticlockwise. Mshale kutoka mwanzo hadi hatua ya mwisho ni kinachoitwa E2. Inaunda kipenyo cha mduara. Kielelezo c kinachoitwa 5 na 2 pi E2 sawa na N delta E0.
    Kielelezo\(\PageIndex{2}\): michoro za Phasor (pamoja na phasors 30) kwa pointi mbalimbali kwenye muundo wa diffraction moja-slit. Mzunguko mingi unaozunguka mduara uliotolewa umetenganishwa kidogo ili fasors ziweze kuonekana. (a) Central upeo, (b) kiwango cha chini kwanza, (c) kwanza ya kiwango cha juu zaidi ya kiwango cha juu ya kati, (d) kima cha chini cha pili, na (e) upeo wa pili zaidi ya kiwango cha juu ya kati.

    Maxima miwili ijayo zaidi ya maxima ya kati yanawakilishwa na michoro ya awamu ya sehemu (c) na (e). Katika sehemu (c), awamu zimezunguka kupitia\(\phi = 3\pi\) rad na zimeunda awamu ya matokeo ya ukubwa\(E_1\). Urefu wa arc iliyoundwa na phasors ni\(N\Delta E_0\). Kwa kuwa hii inalingana na mzunguko wa 1.5 karibu na mduara wa kipenyo\(E_1\), tuna

    \[\dfrac{3}{2} \pi E_1 = N \Delta E_0, \nonumber \]

    kwa hivyo

    \[E_1 = \dfrac{2N\Delta E_0}{3\pi} \nonumber \]

    na

    \[I_1 = \dfrac{1}{2\mu_0 c}E_1^2 = \dfrac{4(N\Delta E_0)^2}{(9\pi^2)(2\mu_0c)} = 0.045 I_0, \nonumber \]

    wapi

    \[I_0 = \dfrac{(N\Delta E_0)^2}{2\mu_0 c}. \nonumber \]

    Katika sehemu (e), awamu zimezungushwa kwa njia ya\(\phi = 5\pi\) rad, sawa na mzunguko wa 2.5 karibu na mduara wa kipenyo\(E_2\) na urefu wa arc\(N\Delta E_0\). Hii inasababisha\(I_2 = 0.016 I_0\). Ushahidi umesalia kama zoezi kwa mwanafunzi (Zoezi 4.119).

    Hizi maxima mbili kweli yanahusiana na maadili ya kidogo chini ya\(3\pi\) rad na\(5\pi\) rad. Kwa kuwa urefu wa jumla wa arc ya mchoro wa phasor daima\(N \Delta E_0\), radius ya arc inapungua kama\(ϕ\) ongezeko. Matokeo yake,\(E_1\) na\(E_2\) kugeuka kuwa kubwa zaidi kwa arcs ambazo hazijapigwa kabisa kupitia\(3\pi\) rad na\(5\pi\) rad, kwa mtiririko huo. Maadili halisi ya\(ϕ\) kwa maxima yanachunguzwa katika Zoezi 4.120. Katika kutatua tatizo hilo, utapata kwamba wao ni chini ya, lakini karibu sana na,\(\phi = 3\pi, \, 5\pi, \, 7\pi,\)... rad.

    Ili kuhesabu kiwango kwa hatua ya kiholela\(P\) kwenye skrini, tunarudi kwenye mchoro wa phasor wa Kielelezo\(\PageIndex{1}\). Kwa kuwa arc hupunguza angle katikati ya mduara,

    \[N\Delta E_0 = r\phi \label{eq10} \]

    na

    \[\sin \left(\dfrac{\phi}{2}\right) = \dfrac{E}{2r}. \label{eq11} \]

    \(E\)wapi amplitude ya shamba la matokeo. Kutatua Equation\ ref {eq11} kwa\(E\) na kisha kubadilisha\(r\) kutoka Equation\ ref {eq10}, tunaona

    \[\begin{align*} E &= 2r \, \sin \, \dfrac{\phi}{2} \\[5pt] &= 2\dfrac{N\Delta E_0}{\phi} \sin \, \dfrac{\phi}{2}. \end{align*} \nonumber \]

    Sasa kufafanua

    \[\beta = \dfrac{\phi}{2} = \dfrac{\pi a \, \sin \, \theta}{\lambda} \label{4.2} \]

    tunapata

    \[E = N\Delta E_0 \dfrac{\sin \, \beta}{\beta} \label{eq15} \]

    Equation\ ref {eq15} inahusiana amplitude ya shamba matokeo wakati wowote katika muundo wa diffraction kwa amplitude\(N \Delta E_0\) katika upeo wa kati. Upeo ni sawia na mraba wa amplitude, hivyo

    \[I = I_0 \left(\dfrac{\sin \, \beta}{\beta}\right)^2 \label{eq20} \]

    ambapo\(I_0 = (N\delta E_0)^2/2\mu_0 c\) ni ukubwa katikati ya muundo.

    Kwa upeo wa kati, = 0, β pia ni sifuri na tunaona kutoka utawala wa l'Hôpital kwamba\(\lim_{\beta \rightarrow 0}(sin \, \beta/\beta) = 1\), ili\(lim_{\phi \rightarrow 0}I = I_0\). Kwa kiwango cha juu ya,\(\phi = 3\pi\) rad, tuna\(\beta = 3\pi/2\) rad na wakati kubadilishwa katika Equation\ ref {eq20}, ni mavuno

    \[I_1 = I_0 \left(\dfrac{\sin \, 3\pi/2}{3\pi/2}\right)^2 = 0.045 I_0, \nonumber \]

    kwa makubaliano na kile tulichopata mapema katika sehemu hii kwa kutumia kipenyo na mzunguko wa michoro za awamu. Kubadilisha\(\phi = 5\pi\) rad katika Equation\ ref {eq20} mavuno matokeo sawa kwa\(I_2\).

    Mpango wa Equation\ ref {eq20} inavyoonekana katika Kielelezo\(\PageIndex{3}\) na moja kwa moja chini ni picha ya muundo halisi wa diffraction. Kumbuka kwamba kilele kati ni mkali zaidi kuliko wengine, na kwamba zeros ya muundo ziko katika maeneo hayo ambapo\(sin \, \beta = 0\), ambayo hutokea wakati\(\beta = m\pi\) rad. Hii inalingana na

    \[\dfrac{\pi a \, \sin \theta}{\lambda} = m\pi, \nonumber \]

    au

    \[a \, \sin \, \theta = m \lambda, \nonumber \]

    ambayo sisi inayotokana na kuingiliwa uharibifu au watakata moja hapo awali.

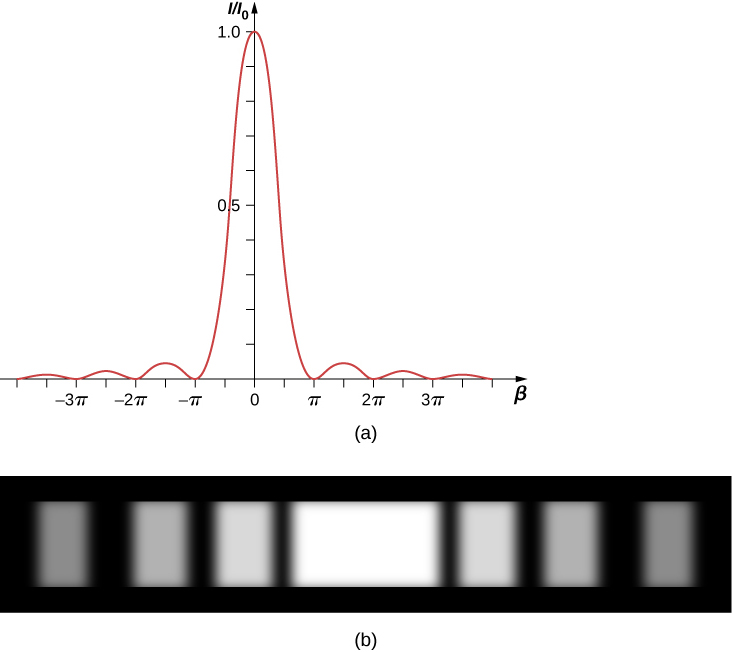
    Kielelezo a inaonyesha graph ya mimi na I0 dhidi beta. Kuna crest katikati ya grafu katika beta sawa na 0. Thamani ya y ya hii ni 1. Grafu ina ripples pande zote mbili za hii ambayo kukua ndogo kama wewe kwenda nje. Grafu ina zero chini ya 3 pi, minus 2 pi, minus pi, pi, 2 pi, 3 pi. Kielelezo b kinaonyesha mstari na mikoa mbadala ya mwanga na giza. Sehemu kuu ni mkali zaidi.
    Kielelezo\(\PageIndex{3}\): (a) Usambazaji wa kiwango cha mahesabu ya muundo wa diffraction moja-kupasuka. (b) mfano halisi wa diffraction.
    Mfano\(\PageIndex{1}\): Intensity in Single-Slit Diffraction

    Mwanga wa wavelength 550 nm hupita kupitia fungu la upana 2.00 μm na hutoa muundo wa diffraction sawa na ule ulioonyeshwa kwenye Kielelezo\(\PageIndex{3a}\).

    1. Pata maeneo ya minima miwili ya kwanza kulingana na angle kutoka upeo wa kati.
    2. Kuamua kiwango jamaa na upeo wa kati katika hatua nusu kati ya minima hizi mbili.

    Mkakati

    Kima cha chini kinatolewa na Equation 4.2.1,\(a \, sin \, \theta = m\lambda\). Minima mbili za kwanza ni kwa m = 1 na m = 2. Equation\ ref {eq20} na Equation\ ref {4.2} inaweza kutumika kuamua kiwango mara moja angle imekuwa kazi nje.

    Suluhisho
    1. Kutatua Equation 4.2.1 kwa ρ\(\theta_m = \sin^{-1}(m\lambda/a)\) inatupa, ili

      \[\theta_1 = \sin^{-1} \left(\dfrac{(+1)(550 \times 10^{-9} m)}{2.00 \times 10^{-6}m}\right) = +16.0° \nonumber \]

      na

      \[\theta_2 = \sin^{-1} \left(\dfrac{(+2)(550 \times 10^{-9}m)}{2.00 \times 10^{-6}m}\right) = +33.4°. \nonumber \]

    2. Nusu ya nusu kati\(\theta_1\) na\(\theta_2\) ni

      \[\theta = (\theta_1 + \theta_2) /2 = (16.0° + 33.4°)/2 = 24.7°. \nonumber \]

    Equation\ ref {4.2} anatoa

    \[\beta = \dfrac{\pi a \, sin \, \theta}{\lambda} = \dfrac{\pi (2.00 \times 10^{-6}m) \, \sin \, (24.7°)}{(550 \times 10^{-9}m)} = 1.52\pi \, or \, 4.77 \, rad. \nonumber \]

    Kutoka Equation\ ref {eq20}, tunaweza kuhesabu

    \[\dfrac{I}{I_0} = \left(\dfrac{\sin \, \beta}{\beta}\right)^2 = \left(\dfrac{\sin \, (4.77)}{4.77}\right)^2 = \left(\dfrac{-0.9985}{4.77}\right)^2 = 0.044. \nonumber \]

    Umuhimu

    Msimamo huu, nusu kati ya minima mbili, ni karibu sana na eneo la kiwango cha juu, kinachotarajiwa karibu\(\beta = 3\pi/2\), au\(1.5\pi\).

    Zoezi\(\PageIndex{1}\)

    Kwa majaribio katika Mfano\(\PageIndex{1}\), kwa pembe gani kutoka katikati ni kiwango cha juu cha tatu na ni kiwango gani kinachohusiana na kiwango cha juu cha kati?

    Jibu

    \(74.3^o\),\(0.0083 I_0\)

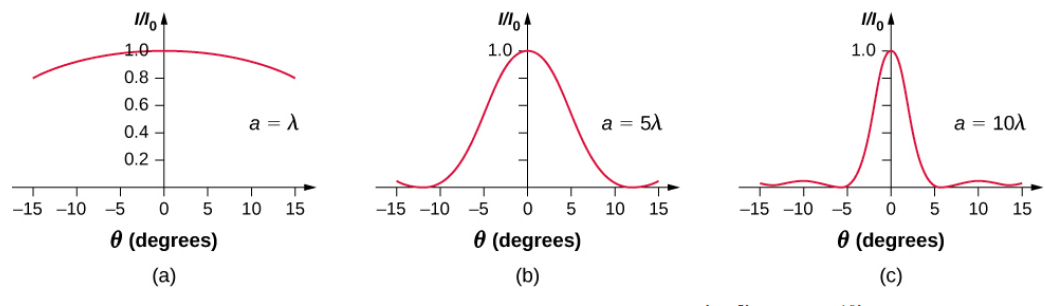
    Kama watakata upana\(a\) ni mbalimbali, mabadiliko kiwango usambazaji, kama inavyoonekana katika Kielelezo\(\PageIndex{4}\). Kilele cha kati kinashirikiwa juu ya kanda kutoka\(sin \, \theta = -\lambda/a\) hadi\(sin \, \theta = +\lambda/a\). Kwa ndogo ρ, hii inalingana na upana wa angular\(\Delta \theta \approx 2\lambda /a\). Kwa hiyo, ongezeko la upana wa upana hupungua kwa kupungua kwa upana wa kilele cha kati. Kwa kupasuka kwa λ, kilele cha kati ni mkali sana, ambapo ikiwa ≈ λ, inakuwa pana kabisa.

    Takwimu kupitia c show grafu ya mimi na I0 dhidi theta katika digrii. Kila mmoja ana kiumbe cha wimbi na thamani y 1 saa x = 0. Kielelezo a, kinachoitwa sawa na lambda ina arc pana. Kielelezo b, kinachoitwa sawa na 5 lambda ina kiumbe nyembamba. Ina zero takribani kati ya 10 na 15 na kati ya minus 10 na minus 15. Kielelezo c, kinachoitwa sawa na 10 lambda ina kiumbe nyembamba. Ina zero kwa pamoja na chini ya 5, takribani kati ya 10 na 15 na kati ya 10 na chini ya 15.
    Kielelezo\(\PageIndex{4}\): Mwelekeo wa diffraction moja-Slit kwa upana mbalimbali watakata. Kama upana wa fungu unaongezeka kutoka =λ hadi 5λ halafu hadi 10λ, upana wa kilele cha kati hupungua kadiri pembe kwa minima ya kwanza inapungua kama ilivyotabiriwa na Ulinganisho 4.2.1.
    Diffraction Simulation

    Jaribio la diffraction katika optics linaweza kuhitaji maandalizi mengi lakini simulation hii na Andrew Duffy hutoa si tu kuanzisha haraka lakini pia uwezo wa kubadilisha upana wa watakata mara moja. Run simulation na kuchagua “Single watakata.” Unaweza kurekebisha upana wa vipande na kuona athari kwenye muundo wa diffraction kwenye skrini na kama grafu.