Skip to main content
Global

2.8: Mchapishaji Rahisi

  1. Last updated
  2. Save as PDF
  • Page ID
    175827

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kuelewa optics ya mkuza rahisi
    • Fanya picha iliyoundwa na mkuza rahisi

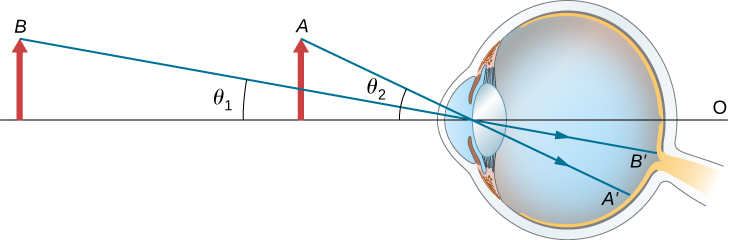
    Ukubwa wa dhahiri wa kitu kinachojulikana kwa jicho hutegemea angle kitu kinachotokana na jicho. Kama inavyoonekana katika Kielelezo\(\PageIndex{1}\), kitu\(A\) katika subtends angle kubwa kutoka jicho kuliko wakati ni nafasi katika hatua\(B\). Hivyo, kitu katika\(A\) fomu picha kubwa juu ya retina (tazama\(OA′\)) kuliko wakati ni nafasi katika\(B\) (tazama\(OB′\)). Hivyo, vitu kwamba subtend pembe kubwa kutoka jicho kuonekana kubwa kwa sababu wao kuunda picha kubwa juu ya retina.

    Vitu viwili vya ukubwa sawa vinaonyeshwa mbele ya jicho. Kitu A ni karibu na jicho na hufanya angle theta 2 na mhimili wa macho. Kitu B ni mbali zaidi na hufanya theta ya angle 1 na mhimili wa macho. Ndani ya jicho, mionzi hupiga retina. Ray B mkuu ni karibu na mhimili wa macho kuliko ray A mkuu.
    Kielelezo\(\PageIndex{1}\): Ukubwa unaojulikana kwa jicho ni kuamua na angle subtended na kitu. Picha iliyoundwa kwenye retina na kitu katika\(A\) ni kubwa kuliko picha iliyoundwa kwenye retina na kitu kimoja kilichowekwa kwenye B (ikilinganishwa na urefu wa picha\(OA′\) hadi\(OB′\)).

    Tumeona kwamba, wakati kitu ni kuwekwa ndani ya focal urefu wa mbonyeo Lens, picha yake ni virtual, wima, na kubwa kuliko kitu (tazama sehemu (b) ya Kielelezo hiki). Hivyo, wakati picha hiyo zinazozalishwa na lens mbonyeo hutumika kama kitu kwa jicho, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\), picha juu ya retina ni wazi, kwa sababu picha zinazozalishwa na Lens subtends angle kubwa katika jicho kuliko kitu. Lens ya mbonyeo inayotumiwa kwa kusudi hili inaitwa kioo cha kukuza au kikuza rahisi.

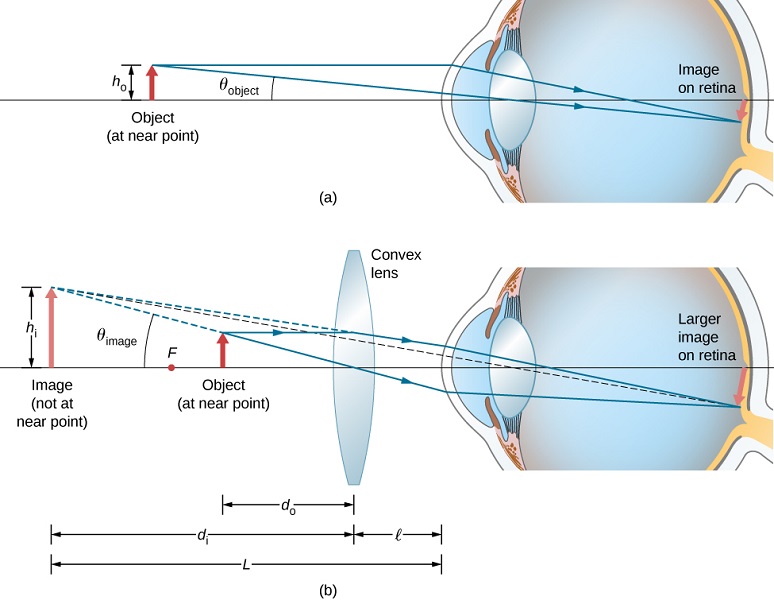
    Kielelezo a inaonyesha kitu kilicho na urefu h 0 mbele ya jicho, karibu. Picha ambayo ni ndogo kuliko kitu hutengenezwa kwenye retina. Kielelezo b kinaonyesha lens bi-convex kati ya jicho na kitu. Mionzi kutoka kwa kitu hupitia hili na kuingia jicho ili kuunda picha kubwa kwenye retina. Upanuzi wa nyuma wa mionzi iliyopotoka na lens hujiunga nyuma ya kitu ili kuunda picha ambayo ni kubwa kuliko kitu. Umbali wa picha hii kutoka kwa lens ni d subscript i na ile ya kitu kutoka lens ni d subscript o. umbali wa Lens kutoka jicho ni l. umbali wa picha kutoka jicho ni L. urefu wa picha ni h subscript i.
    Kielelezo\(\PageIndex{2}\): Kikuza rahisi ni lens ya mbonyeo inayotumiwa kuzalisha picha iliyozidi ya kitu kwenye retina. (a) Kwa lens hakuna convex, kitu subtends angle\(θ_{object}\) kutoka jicho. (b) Kwa lens ya mbonyeo mahali, picha iliyozalishwa na lens ya mbonyeo hupunguza angle\(θ_{image}\) kutoka kwa jicho, na\(θ_{image}> θ_{object}\). Hivyo, picha kwenye retina ni kubwa na lens ya convex mahali.

    Kwa akaunti ya ukuzaji wa lens kukuza, sisi kulinganisha angle subtended na picha (iliyoundwa na lens) na angle subtended na kitu (kutazamwa bila lens), kama inavyoonekana katika Kielelezo\(\PageIndex{1a}\). Tunadhani kwamba kitu iko karibu na jicho, kwa sababu hii ni umbali wa kitu ambacho jicho lisilosaidiwa linaweza kuunda picha kubwa zaidi kwenye retina. Tutalinganisha picha zilizotukuzwa zilizoundwa na lens na ukubwa huu wa picha ya juu kwa jicho lisilosaidiwa. Kukuza picha wakati wa kuzingatiwa na jicho ni ukuzaji wa angular\(M\), ambao hufafanuliwa na uwiano wa angle\(θ_{image}\) iliyopunguzwa na picha kwa angle\(θ_{object}\) iliyowekwa na kitu:

    \[M=\dfrac{θ_{image}}{θ_{object}}. \nonumber \]

    Fikiria hali iliyoonyeshwa kwenye Kielelezo\(\PageIndex{1b}\). Lens ya kukuza inafanyika umbali\(ℓ\) kutoka kwa jicho, na picha iliyozalishwa na mkuza huunda umbali\(L\) kutoka kwa jicho. Tunataka kuhesabu ukuzaji wa angular kwa yoyote ya kiholela\(L\) na\(ℓ\). Katika makadirio ya angle ndogo, ukubwa\(θ_{image}\) wa angular wa picha ni\(h_i/L\). Ukubwa\(θ_{object}\) wa angular wa kitu kilicho karibu ni\(θ_{object}=h_o/25\,cm\). Ukuaji wa angular ni basi

    \[\underbrace{ M=\dfrac{θ_{image}}{θ_{object}}=\dfrac{h_i(25cm)}{Lh_o}}_{\text{angular magnification}} . \label{angular magnification} \]

    Kutumia ufafanuzi wa ukuzaji wa mstari

    \[m=−\dfrac{d_i}{d_o}=\dfrac{h_i}{h_o} \label{mag} \]

    na equation nyembamba-lens

    \[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f} \nonumber \]

    tunakuja kwenye maneno yafuatayo kwa ukuzaji wa angular wa lens ya kukuza:

    \[\begin{align} M&= \left(−\dfrac{d_i}{d_o}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &=−d_i\left(\dfrac{1}{f}−\dfrac{1}{d_i}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &= \left(1−\dfrac{d_i}{f}\right)\left(\dfrac{25\,cm}{L}\right) \label{eq10} \end{align} \]

    Kutoka Kielelezo\(\PageIndex{1b}\), tunaona kwamba thamani kamili ya umbali wa picha ni\(|d_i|=L−ℓ\). Kumbuka kwamba\(d_i<0\) kwa sababu picha ni virtual, hivyo tunaweza kugawa kwa thamani kamili kwa kuingiza wazi ishara minus:

    \[−d_i=L−ℓ. \label{eq34} \]

    Kuingiza Equation\ ref {eq34} katika Equation\ ref {eq10} inatupa equation ya mwisho kwa ukuzaji wa angular wa lens ya kukuza:

    \[M=\left(\dfrac{25\,cm}{L}\right) \left(1+\dfrac{L−ℓ}{f} \right). \label{eq12} \]

    Kumbuka kwamba wingi wote katika equation hii lazima walionyesha kwa sentimita. Mara nyingi, tunataka picha kuwa umbali wa karibu (kwa mfano,\(L=25\,cm\)) ili kupata ukuzaji wa kiwango cha juu, na tunashikilia lens ya kukuza karibu na jicho (\(ℓ=0\)). Katika kesi hii, Equation\ ref {eq12} inatoa

    \[M=1+\dfrac{25\,cm}{f} \label{eq13} \]

    ambayo inaonyesha kwamba ukuzaji mkubwa hutokea kwa lens na urefu mfupi zaidi. Kwa kuongeza, wakati picha iko umbali wa karibu na hatua na lens inafanyika karibu na jicho (\(ℓ=0\)), basi\(L=d_i=25\,cm\) na Equation\ ref {eq12} inakuwa

    \[M=\dfrac{h_i}{h_o}=m \label{eq14} \]

    \(m\)wapi ukuzaji wa mstari (Equation\ ref {mag}) uliotokana hapo awali kwa vioo vya spherical na lenses nyembamba. Hali nyingine muhimu ni wakati picha iko kwenye infinity (\(L=\infty\)). Equation\ ref {eq12} kisha inachukua fomu

    \[M(L=\infty)=\dfrac{25\,cm}{f}. \label{eq15} \]

    Kukuza kwa matokeo ni tu uwiano wa umbali wa karibu na urefu wa urefu wa lens ya kukuza, hivyo lens yenye urefu mfupi wa focal hutoa ukuzaji wenye nguvu. Ingawa ukuzaji huu ni mdogo kwa 1 kuliko ukuzaji uliopatikana kwa picha kwenye hatua ya karibu, hutoa hali nzuri zaidi ya kutazama, kwa sababu jicho linafuatana wakati wa kutazama kitu cha mbali.

    Kwa kulinganisha equations\ ref {eq13} na\ ref {eq15}, tunaona kwamba upeo wa ukuzaji wa angular wa lens inayobadilika ni

    \[\dfrac{25cm}{f} ≤ M ≤1+\dfrac{25cm}{f}. \nonumber \]

    Mfano\(\PageIndex{1}\): Magnifying a Diamond

    Jeweler inataka kukagua almasi ya kipenyo cha 3.0-mm-na kikuza. Almasi inafanyika kwenye eneo la karibu la jiwe (25 cm), na jiwe linashikilia lens ya kukuza karibu na jicho lake.

    1. Je! Urefu wa msingi wa lens ya kukuza unapaswa kuona picha ya kipenyo cha 15-mm-kipenyo cha almasi?
    2. Je, urefu wa msingi wa lens ya kukuza unapaswa kupata ukuzaji wa 10×?

    Mkakati

    Tunahitaji kuamua ukuzaji unaohitajika wa mkufu. Kwa sababu jeweler inashikilia lenzi ya kukuza karibu na jicho lake, tunaweza kutumia Equation\ ref {eq13} ili kupata urefu wa focal wa lens ya kukuza.

    Suluhisho

    a. required linear ukuzaji ni uwiano wa taka picha kipenyo kwa almasi ya kipenyo halisi (Equation\ ref {eq15}). Kwa sababu jiwe linashikilia lens ya kukuza karibu na jicho lake na fomu za picha katika hatua yake ya karibu, ukuzaji wa mstari ni sawa na ukuzaji wa angular, hivyo

    \[\begin{align*} M &=m=\dfrac{h_i}{h_o}\\[4pt] &=\dfrac{15\,mm}{3.0\,mm} \\[4pt] &=5.0.\end{align*} \nonumber \]

    Urefu wa focal f wa lens ya kukuza inaweza kuhesabiwa kwa kutatua Equation\ ref {eq13} kwa\(f\), ambayo inatoa

    \[M=1+\dfrac{25\,cm}{f} \nonumber \]

    \[\begin{align*} f&=\dfrac{25\,cm}{M−1} \\[4pt] &= \dfrac{25\,cm}{5.0−1} \\[4pt] &= 6.3\,cm \end{align*} \nonumber \]

    b Ili kupata picha iliyotukuzwa kwa sababu ya kumi, sisi tena kutatua Equation\ ref {eq13} kwa\(f\), lakini wakati huu tunatumia\(M=10\). Matokeo yake ni

    \[\begin{align*} f &=\dfrac{25\,cm}{M−1} \\[4pt] &=\dfrac{25\,cm}{10−1} \\[4pt] &=2.8\,cm. \end{align*} \nonumber \]

    Umuhimu

    Kumbuka kuwa ukuzaji mkubwa unapatikana kwa kutumia lens yenye urefu mdogo. Kwa hiyo tunahitaji kutumia lens yenye radii ya curvature ambayo ni chini ya sentimita chache na kuiweka karibu sana na jicho letu. Hii si rahisi sana. Microscope ya kiwanja, iliyochunguzwa katika sehemu inayofuata, inaweza kushinda tatizo hili.