7.4: Ulinganisho wa mistari ya Wima na ya usawa
- Page ID
- 164592
Ulinganisho wa mstari wa wima ni wa fomu\(x = c\), wapi\(c\) nambari yoyote halisi. Mstari wa wima daima utazunguka\(x\) -axis kwa uhakika\((c, 0)\). Mteremko wa mstari wa wima haujafafanuliwa.
Pata mteremko wa mstari\(x = 4\) na graph mstari.
Suluhisho
\(x = 4\)ni grafu ya mstari wa wima kama inavyoonekana katika takwimu hapa chini.
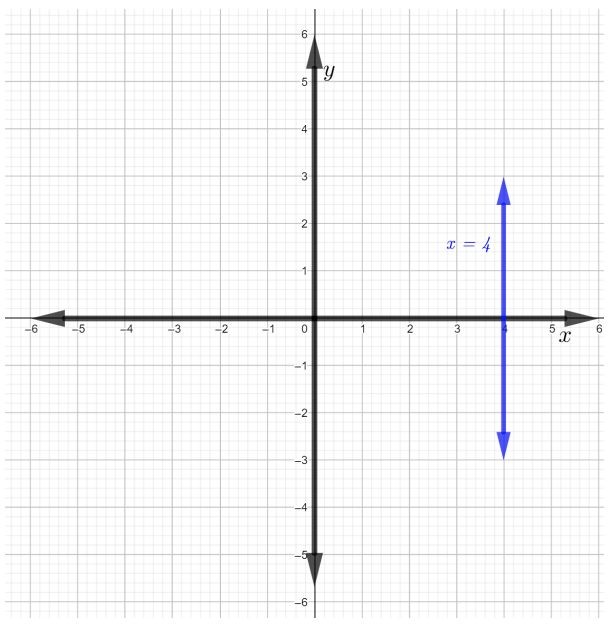
Ili kupata mteremko wa mstari\(x = 4\) chagua pointi mbili tofauti kwenye mstari. Hebu pointi ziwe\((4, −1)\) na\((4, 3)\). Kutumia mteremko wa fomu ya mstari,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3 − (−1)}{4 − 4} &\text{Substitute values} \\ &= \dfrac{4}{0} &\text{Simplify} \end{array}\)
Sasa, ikiwa\(4\) imegawanywa na\(0\), hii ni sawa na kuuliza swali,” ni namba gani mara zero inatoa\(4\)?” jibu ni, hakuna idadi hiyo. Idara ya sifuri haijulikani, na mteremko wa mstari wa wima\(x = 4\) haujafafanuliwa.
Ulinganisho wa mstari usio na usawa ni wa fomu\(y = k\), wapi\(k\) nambari yoyote halisi. Mstari wa usawa utazunguka kila wakati\(y\) -axis kwa uhakika\((0, k)\). Mteremko wa mstari usio na usawa ni Zero.
Pata mteremko wa mstari unaopita kupitia pointi\((−3, −2)\) na\((4, −2)\). Panda pointi na grafu mstari unaopita kupitia kwao.
Suluhisho
Tumia mteremko wa fomu ya mstari. Hivyo,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{(−2) − (−2)}{4 − (−3)} &\text{Substitute values} \\ &= \dfrac{0}{7} &\text{Simplify} \\ &= 0 &\text{\(0\)imegawanywa na nambari yoyote isiyo ya zero ni sawa na sifuri}\ mwisho {array}\)
Kwa hiyo, mstari unaopita kupitia pointi mbili zilizopewa ni mstari wa usawa, na mteremko sawa na sifuri, kama inavyoonekana katika takwimu hapa chini.
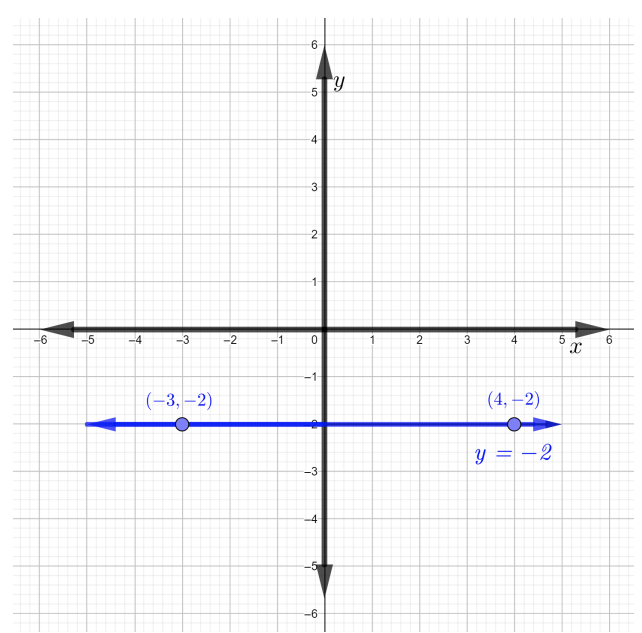
Graph mstari\(y − 3 = 0\) na kupata mteremko wake.
Suluhisho
Mstari\(y − 3 = 0\) unaweza kuandikwa kama\(y = 3\) (\(3\)kuongeza pande zote mbili za equation). Mstari\(y = 3\) ni mstari usio na usawa, kama inavyoonekana katika takwimu hapa chini.
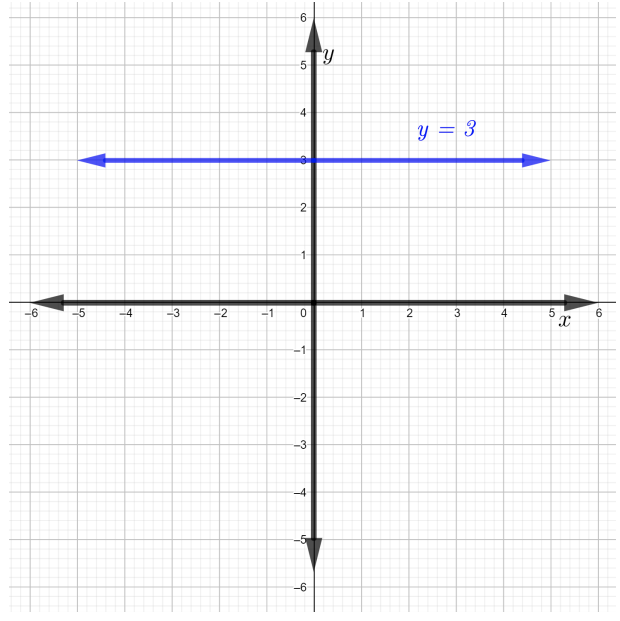
Sasa, ili kupata mteremko, chagua pointi mbili tofauti kwenye mstari\(y = 3\). Fikiria pointi\((0, 3)\) na\((3, 3)\). Hivyo,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3-3}{3-0} &\text{Substitute values} \\ &= \dfrac{0}{2} &\text{Simplify} \\ &= 0 &\text{\(0\)imegawanywa na nambari yoyote isiyo ya zero ni sawa na sifuri}\ mwisho {array}\)
Kwa hiyo, mteremko wa mstari uliopewa ni\(m = 0.\)
Pata mteremko wa kila mstari.
- \(x = −\dfrac{1}{2}\)
- \(y − 1 = 0\)
- \(x + 7 = 10\)
- \(y + 2 = −9\)
- Pata mteremko wa mstari unaopita kupitia pointi\((−4, 1)\) na\((2, 1)\). Panda pointi na grafu mstari unaopita kupitia kwao.
- Pata mteremko wa mstari unaopita kupitia pointi\((−3, 5)\) na\((−3, −7)\). Panda pointi na grafu mstari unaopita kupitia kwao.


