7.5: Fomu za Equation ya Line
- Page ID
- 164597
Sehemu iliyopita ilielezea usawa wa mistari ya wima na ya usawa. Sasa gundua aina tatu zaidi za equations ya mstari, yaani, Fomu ya Slope-Intercept, Fomu ya Point-Slope, na Fomu ya Standard.
Slope-Intercept Fomu ya Equation ya Line
Fomu ya Slope-Intercept ya equation ya mstari ni ya fomu:
\[y = mx + b \nonumber \]
Ambapo\(m\) ni mteremko wa mstari na\((0, b)\) ni\(y\) -intercept.
Kumbuka kuwa\(y\) -intercept ni hatua ambapo mstari intersect\(y\) -axis, kwamba ni wakati\(x = 0\).
Andika equation ya mstari na mteremko uliopewa na\(y\) -intercepts.
- mteremko =\(5\)\(y\); -kukatiza\((0, \dfrac{1}{2})\)
- mteremko =\(−\dfrac{5}{6}\)\(y\); - kukatiza\((0, −\dfrac{3}{4})\)
Suluhisho
- \(m = 5\)na\(b = \dfrac{1}{2}\)
equation ya mstari ni ya kwa\(y = mx + b\). Hivyo,
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute \(m = 5\)na\(b = \dfrac{1}{2}\)}\ mwisho {safu}\)
Kwa hiyo,\(y = 5x + \dfrac{1}{2}\) ni equation ya mstari na mteremko kutokana na\(y\) -intercept.
- Kutokana\(m = −\dfrac{5}{6}\) na\(b = −\dfrac{3}{4}\)
Hivyo,
\(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}\)
Kwa hiyo,\(y = −\dfrac{5}{6}x − \dfrac{3}{4}\) ni equation ya mstari na mteremko kutokana na\(y\) -intercept.
Tambua mteremko\(y\) na ukataze basi, uitumie kupiga kila mstari.
- \(y = −2x + 4\)
- \(5y − 3x = 10\)
Suluhisho
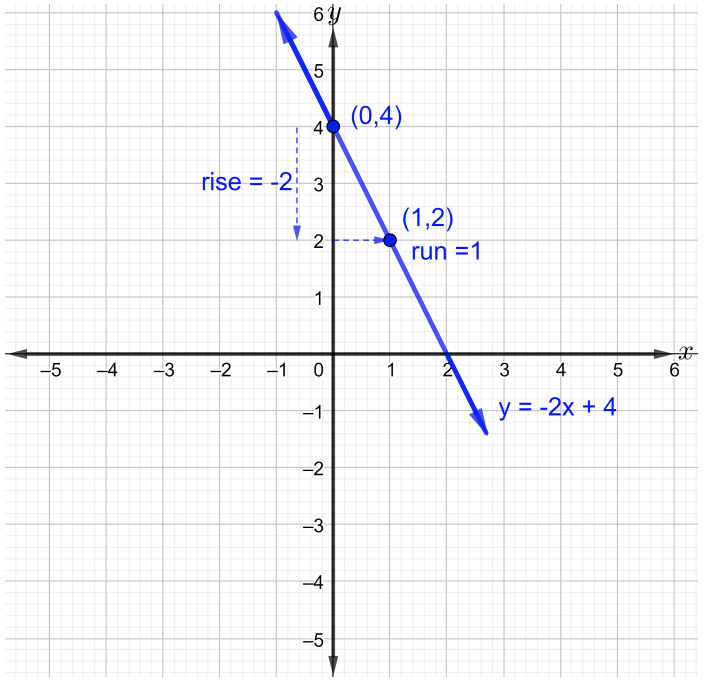
Taarifa kwamba equation linear kupewa ni katika mteremka-intercept fomu. Hivyo,\(m = −2\) au equivalently,\(m = −\dfrac{2}{1}\) na\(b = 4\)
\(m\)ni mteremko wa mstari, basi\(m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}\). Ili grafu mstari, njama angalau pointi mbili. Anza saa\(y\) -intercept\((0, 4)\) na hoja chini\(2\) kitengo kisha hoja ya\(1\) kitengo haki ya njama hatua ya pili. Sasa jiunge na pointi mbili kwa mstari wa moja kwa moja kama inavyoonekana katika takwimu hapa chini.
b Angalia kwamba haijulikani jinsi ya kutambua mteremko na\(y\) -intercept katika equation hii iliyotolewa linear kwa sababu si katika mteremka-intercept fomu. Hivyo, kutatua\(y\) kwa kuwa na equation katika fomu mteremka-intercept kama ifuatavyo,
\(\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add \(3x\)kwa pande zote mbili za equation}\\ &y =\ dfrac {3} {5} x - 2 &\ maandishi {Gawanya maneno yote\(5\) kwa kujitenga\(y\)}\ mwisho {array}\)
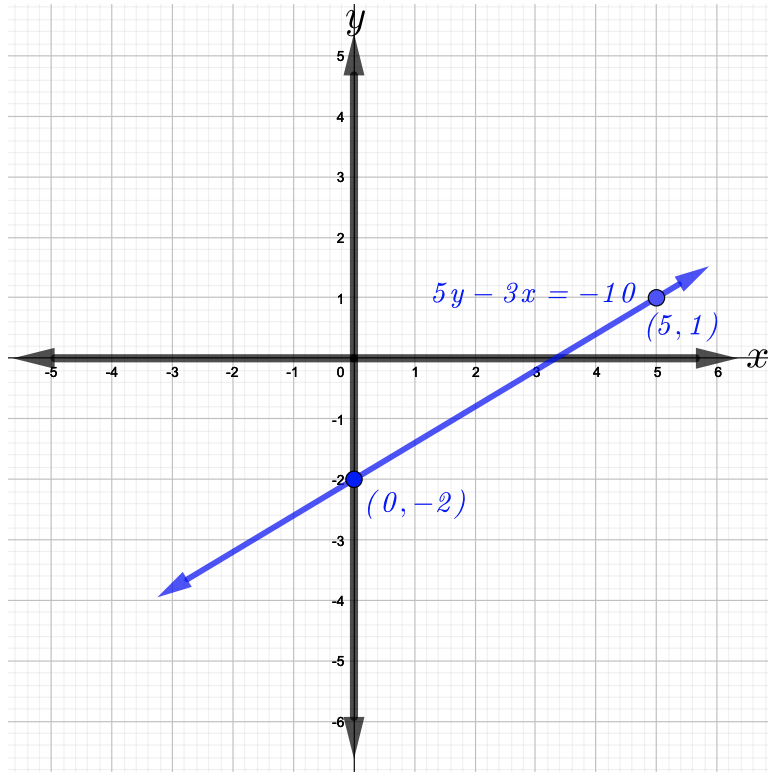
Sasa,\(m = \dfrac{3}{5}\) na\(b = −2\). Anza kwa kupanga njama\(y\) -intercept\((0, −2)\) kisha hoja\(3\)\(5\) vitengo zaidi na vitengo na haki na njama hatua ya pili ambayo ni\((5, 1)\). Sasa, jiunge na pointi mbili, yaani,\((0, −2)\) na\((5, 1)\) kupata grafu ya mstari iliyoonyeshwa kwenye takwimu hapa chini.
Andika equation ya mstari na mteremko uliopewa na\(y\) -intercept.
- mteremko:\(2\)\(y\) -kukatiza:\((0, \dfrac{3}{4})\)
- mteremko:\(\dfrac{5}{7}\)\(y\) -kukatiza:\((0, −6)\)
- mteremko:\(−\dfrac{1}{2}\)\(y\) -kukatiza:\((0, −\dfrac{7}{11} )\)
Tambua mteremko na\(y\) -intercept kisha uitumie kwa graph kila mstari.
- \(y = 5x − 3\)
- \(2y = −6x + 1\)
Fomu ya Point-Slove ya Equation ya Line
Fomu ya Point-Slope ya equation ya mstari wa moja kwa moja ni:
\[y − y_1 = m(x − x_1) \nonumber \]
Ambapo\(m\) ni mteremko wa mstari na\((x_1, y_1)\) ni hatua yoyote kwenye mstari wa moja kwa moja.
Find equation ya kila mstari kupita kwa njia ya hatua fulani na kupewa mteremko.
- Mteremko\(3\) na uhakika\((−1, 8)\)
- Mteremko\(−\dfrac{5}{2}\) na uhakika\((\dfrac{4}{3}, \dfrac{1}{3})\)
Suluhisho
- Ili kupata equation ya mstari kupitia hatua\((−1, 8)\) na mteremko\(m = 3\), tumia fomu ya mteremko wa uhakika kama ifuatavyo:
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute \(m = 3\),\(x_1 = −1\), na\(y_1 = 8\)}\\ &y- 8 = 3 (x + 1) &\ maandishi {Kurahisisha}\\ &y- 8 = 3x + 3 &\ maandishi {Kuzidisha maneno yote kwa haki ya equation na\(3\)}\\ &y = 3x + 11 &\ maandishi {Ongeza\(8\) pande zote mbili za usawa kutenganisha\(y\)}\ mwisho {safu}\)
Kwa hiyo,\(y = 3x + 11\) ni equation ya mstari na mteremko kutokana na uhakika. Mstari ni katika fomu ya kuingilia mteremko.
- Sawa na sehemu a, tumia Fomu ya Point-Slope kama ifuatavyo:
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute \(m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}\), na\(y_1 = −\dfrac{1}{3}\)}\\ &y +\ dfrac {1} {3} = -\ dfrac {5} {2} x +\ dfrac {20} {6} &\ maandishi {Kusambaza na kurahisisha}\\ &y = -\ dfrac {5} {2} x +\ dfrac {20} {6}} -\ dfrac {1} {1} &\ Nakala {3} &\ Nakala {Tract\(\dfrac{1}{3}\) kutoka pande zote mbili}\\ &y = -\ dfrac {5} {2} x + 3 &\ maandishi {Ili kuchanganya sehemu mbili, tazama kwamba LCD\(= 6\).}\\ & &\ maandishi {Kuzidisha nambari na denominator ya\(\dfrac{1}{3}\)\(2\) na kurahisisha:}\\ & &\ Nakala {\(\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3\)}\ mwisho {array}\)
Kwa hiyo,\(y = −\dfrac{5}{2}x + 3\) ni equation ya mstari kwa njia ya kutoa uhakika na mteremko kutokana.
Kupata equation ya pointi line kutokana\((2, 4)\) na\((−3, 9)\).
Kumbuka kwamba mapema katika sura hii alielezea jinsi ya kupata equation ya mstari kupewa mteremko na\(y\) -intercept. Sura hii pia alielezea jinsi ya kupata equation ya mstari kutokana na hatua yoyote juu ya mstari na mteremko. Hivyo, kwa njia zote mbili, mteremko hutolewa.
Suluhisho
Ili kupata equation ya mstari kutokana na pointi zozote mbili kwenye mstari, kwanza tafuta mteremko ukitumia mteremko wa formula ya mstari. Baadaye, tumia fomu ya mteremko wa uhakika na pointi yoyote iliyotolewa. Kwanza, tumia pointi mbili ili kupata mteremko wa mstari. Hebu\((x_1, y_1) = (2, 4)\) na\((x_2, y_2) = (−3, 9)\). Kisha,
\(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}\)
Sasa mteremko imekuwa kupatikana hivyo ijayo kupata equation ya mstari kwa kutumia moja ya pointi fulani. Hivyo,\(m = −1\) na fikiria kutumia hatua\((2, 4)\).
\(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute \(m = −1\)\(x_1 = 2\),\(y_1 = 4\)}\\ &y - 4 = -x + 2 &\ maandishi {Kusambaza\(-1\) kwa maneno yote upande wa kulia}\\ &y = -x + 6 &\ maandishi {Ongeza\(4\) pande zote mbili za equation ili kujitenga\(y\)}\ mwisho {safu}\)
Kwa hiyo,\(y = −x + 6\) ni equation ya mstari kupita kwa njia ya kutoa uhakika na ina mteremka-intercept fomu.
Find equation ya kila mstari kupita kwa njia ya hatua fulani na ina mteremko kupewa.
- Mteremko\(−\dfrac{5}{2}\) na uhakika\((3, 0)\).
- Mteremko\(\dfrac{1}{2}\) na uhakika\((−2, −3)\).
Kupata equation ya mstari kutokana Points zifuatazo.
- \((−9, −3)\)na\((6, −2)\)
- \((4, 1)\)na\((−2, 2)\)
Fomu ya kawaida ya Ulinganisho wa Mstari (AKA Fomu ya jumla ya Equation Linear)
Fomu ya kawaida ya mstari usio na wima iko katika fomu
\[Ax + By = C \nonumber \]
Ambapo\(A\) ni integer chanya,\(B\) na\(C\) ni integers na\(B \neq 0\).
Grafu kila mstari wa equations zifuatazo:
- \(4x − 3y = 6\)
- \(\dfrac{1}{2} − y + 1 = 0\)
Kumbuka kuwa\(x\) -intercept ni hatua ambapo mstari unaingiliana\(x\) -axis. Hiyo ni, wakati\(y = 0\). Hivyo,\(x\) -intercept ni hatua ya fomu\((a, 0)\), wapi\(a\) nambari yoyote halisi.
Suluhisho
- Equation\(4x − 3y = 6\) iko katika fomu ya kawaida. Ili kuchora mstari wa equation iliyotolewa inaweza kuwa inawezekana kutumia njia zaidi ya moja. Kwa mfano, kutatua kwa\(y\) kupata equation katika mteremka-intercept fomu, basi, grafu line. Inawezekana pia kupata pointi mbili, kisha graph mstari. pointi mbili rahisi kupata haraka ni\(x\) na\(y\) intercepts. Kwa hiyo, njia hii inapendekezwa.
Ili kupata\(x\) -intercept, kuweka\(y = 0\) katika equation kupewa na kutatua kwa\(x\) kama ifuatavyo,
\(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute \(y = 0\)}\\ &4x = 6 &\ maandishi {Kurahisisha}\\ &x =\ dfrac {6} {4} &\ maandishi {Gawanya kwa pande\(4\) zote mbili za equation}\\ &x =\ dfrac {3} {2} &\ maandishi {Kurahisisha}\ mwisho {safu}\)
Hivyo,\(x\) -intercept ni hatua\((\dfrac{3}{2}, 0)\)
Sasa, ili kupata\(y\) - intercept, kuweka\(x = 0\) kama ifuatavyo,
\(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute \(x = 0\)}\\ &—3y = 6 &\ maandishi {Kurahisisha}\\ &y = 6 —3 &\ maandishi {Gawanya kwa pande\(−3\) zote mbili za equation}\\ &y = -2 &\ maandishi {Kurahisisha}\ mwisho {safu}\)
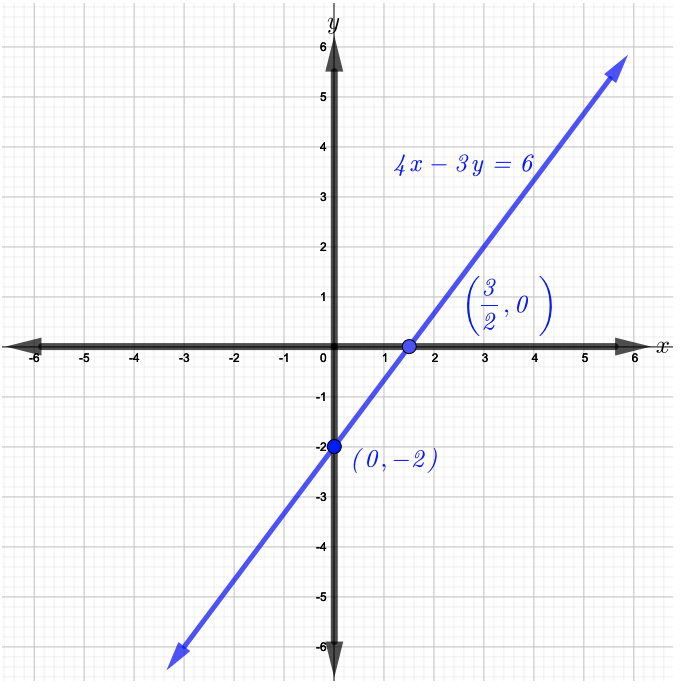
Sasa, njama pointi\((\dfrac{3}{2}, 0)\)\((0, −2)\) na graph mstari wa moja kwa moja unaopita kupitia kwao kama inavyoonekana katika takwimu hapa chini.
Equation\(\dfrac{1}{2} x − y + 1 = 0\) si katika fomu ya kawaida. Hivyo, Ondoa\(1\) kutoka pande zote mbili za equation kuwa na\(\dfrac{1}{2}x − y = −1\) ambayo sasa ni katika hali ya kiwango.
Kwa mara nyingine tena, sawa na sehemu b, kupata\(x\) na\(y\) -intercepts. Kwanza, pata\(x\) -intercept kwa kuweka\(y = 0\) na kutatua kwa\(x\) ifuatavyo.
\( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute \(y = 0\)}\\ &\ dfrac {1} {2} x = -1 &\ maandishi {Kurahisisha}\\ &x = -2 &\ maandishi {Kuzidisha kwa pande\(2\) zote mbili za equation.} \ mwisho {safu}\)
Hivyo,\(x\) -intercept ni uhakika\((−2, 0)\).
Sasa, kuweka\(x = 0\) kupata\(y\) intercept, kama ifuatavyo,
\( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute \(x = 0\)}\\ &-y = -1 &\ Nakala {Kurahisisha}\\ &y = 1 &\ maandishi {Kuzidisha kwa\(-1\).} \ mwisho {safu}\)
Kwa hiyo,\(y\) -intercept ni\((0, 1)\).
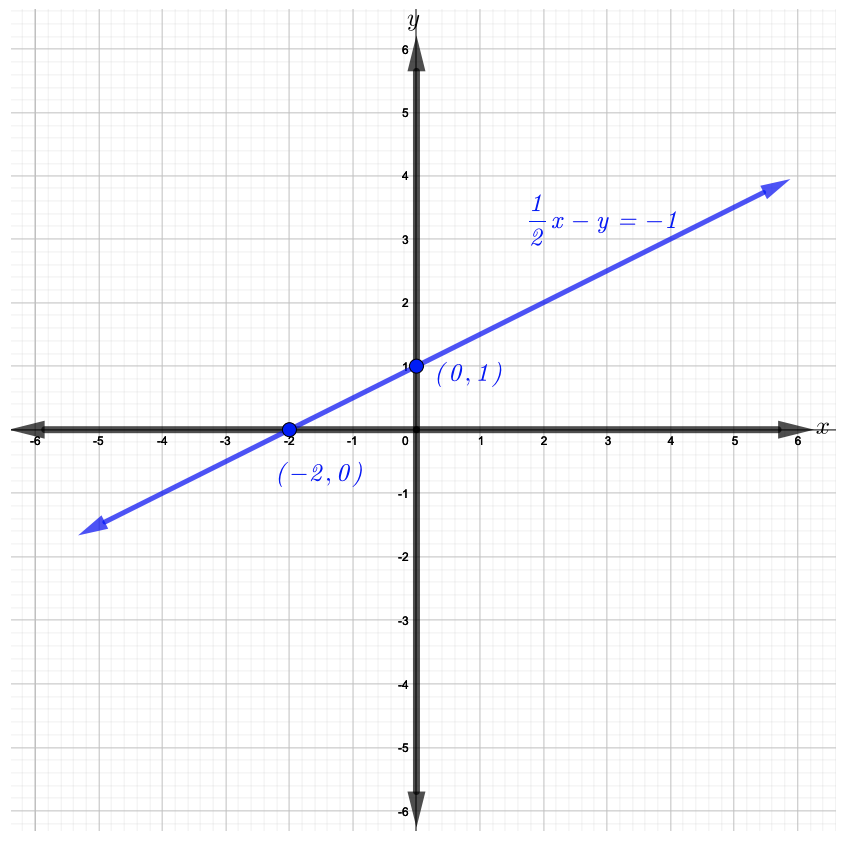
Panda\(x\) na\(y\) -intercepts,\((−2, 0)\) na\((0, 1)\), kisha graph mstari wa moja kwa moja ambayo hupita kupitia kwao kama inavyoonekana katika takwimu hapa chini.
Hakuna kazi ya nyumbani kwa sehemu hii.


