12.4: Utaratibu wa kijiometri na Mfululizo
- Page ID
- 175632
Mwishoni mwa sehemu hii, utaweza:
- Kuamua kama mlolongo ni kijiometri
- Pata neno la jumla (neno)\(n\) la mlolongo wa kijiometri
- Pata jumla ya\(n\) maneno ya kwanza ya mlolongo wa kijiometri
- Pata jumla ya mfululizo usio na kipimo cha kijiometri
- Tumia utaratibu wa kijiometri na mfululizo katika ulimwengu wa kweli
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kurahisisha:\(\frac{24}{32}\).
Kama amekosa tatizo hili, mapitio Mfano 1.24. - Tathmini: a.\(3^{4}\) b\(\left(\frac{1}{2}\right)^{4}\).
Kama amekosa tatizo hili, mapitio Mfano 1.19. - Ikiwa\(f(x)=4 \cdot 3^{x}\), pata.\(f(1)\) b.\(f(2)\) c\(f(3)\).
Kama amekosa tatizo hili, mapitio Mfano 3.49.
Kuamua kama Mlolongo ni Jiometri
Sasa tuko tayari kuangalia aina ya pili ya mlolongo, mlolongo wa kijiometri.
Mlolongo huitwa mlolongo wa kijiometri ikiwa uwiano kati ya maneno ya mfululizo daima ni sawa. Uwiano kati ya maneno mfululizo katika mlolongo wa kijiometri ni\(r\), uwiano wa kawaida, wapi\(n\) ni mkubwa kuliko au sawa na mbili.
Mlolongo wa kijiometri ni mlolongo ambapo uwiano kati ya maneno ya mfululizo daima ni sawa.
Uwiano kati ya maneno mfululizo,\(\frac{a_{n}}{a_{n-1}}\), ni\(r\), uwiano wa kawaida. \(n\)ni kubwa kuliko au sawa na mbili.
Fikiria utaratibu huu.
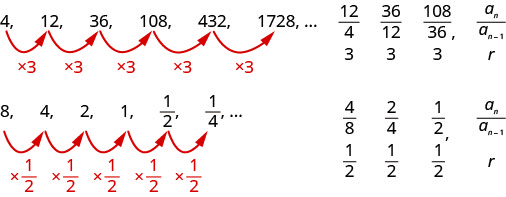
Kuamua kama kila mlolongo ni kijiometri. Ikiwa ndivyo, onyesha uwiano wa kawaida.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
Suluhisho:
Kuamua kama mlolongo ni kijiometri, tunapata uwiano wa maneno mfululizo yaliyoonyeshwa.
Pata uwiano wa maneno mfululizo
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
Mlolongo ni kijiometri. Mgawo wa kawaida ni\(r=2\).
b Pata uwiano wa maneno mfululizo
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
Mlolongo sio kijiometri. Hakuna uwiano wa kawaida.
c Kupata uwiano wa maneno mfululizo
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
Mlolongo ni kijiometri. Uwiano wa kawaida ni\(r=\frac{1}{3}\).
Kuamua kama kila mlolongo ni kijiometri. Ikiwa ndivyo zinaonyesha uwiano wa kawaida.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- Jibu
-
- Mlolongo ni kijiometri na uwiano wa kawaida\(r=3\).
- Mlolongo ni kijiometri na uwiano wa kawaida\(d=\frac{1}{4}\).
- Mlolongo sio kijiometri. Hakuna uwiano wa kawaida.
Kuamua kama kila mlolongo ni kijiometri. Ikiwa ndivyo zinaonyesha uwiano wa kawaida.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Jibu
-
- Mlolongo sio kijiometri. Hakuna uwiano wa kawaida.
- Mlolongo ni kijiometri na uwiano wa kawaida\(r=2\).
- Mlolongo ni kijiometri na uwiano wa kawaida\(r=\frac{1}{2}\).
Kama tunajua muda wa kwanza,\(a_{1}\), na uwiano wa kawaida,\(r\), tunaweza kuorodhesha idadi ya mwisho ya suala la mlolongo.
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(3\) na uwiano wa kawaida ni\(r=−2\).
Suluhisho:
Tunaanza na muda wa kwanza na kuzidisha kwa uwiano wa kawaida. Kisha tunazidisha matokeo hayo kwa uwiano wa kawaida ili kupata muda ujao, na kadhalika.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
Jibu:
Mlolongo ni\(3,-6,12,-24,48, \dots\)
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(7\) na uwiano wa kawaida ni\(r=−3\).
- Jibu
-
\(7,-21,63,-189,567\)
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(6\) na uwiano wa kawaida ni\(r=−4\).
- Jibu
-
\(6,-24,96,-384,1536\)
Pata Muda Mkuu (Muda)\(n\) wa Mlolongo wa Kijiometri
Kama tulivyopata formula kwa muda wa jumla wa mlolongo na mlolongo wa hesabu, tunaweza pia kupata formula kwa muda wa jumla wa mlolongo wa kijiometri.
Hebu tuandike maneno machache ya mlolongo ambapo muda wa kwanza ni\(a_{1}\) na uwiano wa kawaida ni\(r\). Sisi kisha kuangalia kwa mfano.
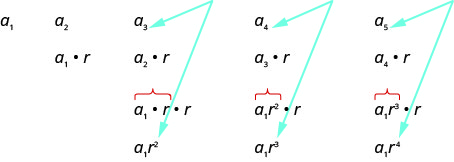
Tunapotafuta mfano katika maneno matano hapo juu, tunaona kwamba kila maneno huanza na\(a_{1}\).
Muda wa kwanza,\(a_{1}\), si kuzidishwa na yoyote\(r\). Katika kipindi cha pili,\(a_{1}\) ni kuongezeka kwa\(r\). Katika muda wa tatu,\(a_{1}\) ni kuongezeka kwa mara\(r\) mbili (\(r⋅r\)au\(r^{2}\)). Katika muda wa nne,\(a_{1}\) huongezeka kwa mara\(r\) tatu (\(r⋅r⋅r\)au\(r^{3}\)) na katika kipindi cha tano,\(a_{1}\) huongezeka kwa mara\(r\) nne. Katika kila muda, idadi ya nyakati huongezeka kwa\(a_{1}\)\(r\) ni moja chini ya idadi ya muda. Hii inatuongoza kwa yafuatayo
\(a_{n}=a_{1} r^{n-1}\)
Neno la jumla la mlolongo wa kijiometri\(a_{1}\) na muda wa kwanza na uwiano wa kawaida\(r\) ni
\(a_{n}=a_{1} r^{n-1}\)
Tutatumia formula hii katika mfano unaofuata ili kupata muda wa kumi na nne wa mlolongo.
Kupata kumi na nne mrefu ya mlolongo ambapo muda wa kwanza ni\(64\) na uwiano wa kawaida ni\(r=\frac{1}{2}\).
Suluhisho:
\(a_{n}=a_{1} r^{n-1}\)
Ili kupata muda wa kumi na nne\(a_{14}\), tumia formula\(a_{1}=64\) na\(r=\frac{1}{2}\).
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
Mbadala katika maadili.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
Kurahisisha.
\(a_{14}=\frac{1}{128}\)
Pata muda wa kumi na tatu wa mlolongo ambapo muda wa kwanza ni\(81\) na uwiano wa kawaida ni\(r=\frac{1}{3}\).
- Jibu
-
\(\frac{1}{6,561}\)
Kupata kumi na mbili mrefu ya mlolongo ambapo muda wa kwanza ni\(256\) na uwiano wa kawaida ni\(r=\frac{1}{4}\).
- Jibu
-
\(\frac{1}{16,384}\)
Wakati mwingine hatujui uwiano wa kawaida na tunapaswa kutumia taarifa iliyotolewa ili kuipata kabla ya kupata muda ulioombwa.
Kupata kumi na mbili mrefu ya mlolongo\(3, 6, 12, 24, 48, 96, …\) Kupata mrefu ujumla kwa mlolongo.
Suluhisho:
Ili kupata muda wa kumi na mbili, tunatumia formula\(a_{n}=a_{1} r^{n-1}\), na hivyo tunahitaji kwanza kuamua\(a_{1}\) na uwiano wa kawaida\(r\).
Muda wa kwanza ni tatu.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
Pata uwiano wa kawaida.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
Ili kupata muda wa kumi na mbili\(a_{12}\), tumia formula\(a_{1}=3\) na\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
Mbadala katika maadili.
\(a_{12}=3 \cdot 2^{12-1}\)
Kurahisisha.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
Pata muda wa jumla. Tunatumia formula\(a_{1}=3\) na\(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
Pata muda wa tisa wa mlolongo\(6, 18, 54, 162, 486, 1,458, … \) Kisha pata muda wa jumla kwa mlolongo.
- Jibu
-
\(a_{9}=39,366 .\)Neno la jumla ni\(a_{n}=6(3)^{n-1}\).
Pata muda wa kumi na moja wa mlolongo\(7, 14, 28, 56, 112, 224, …\) Kisha pata muda wa jumla kwa mlolongo.
- Jibu
-
\(a_{11}=7,168 .\)Neno la jumla ni\(a_{n}=7(2)^{n-1}\).
Pata Jumla ya\(n\) Masharti ya Kwanza ya Mlolongo wa Kijiometri
Tuligundua jumla ya Utaratibu wote wa jumla na mlolongo hesabu. Sasa tutafanya hivyo kwa utaratibu wa kijiometri. Jumla,\(S_{n}\), ya\(n\) maneno ya kwanza ya mlolongo wa kijiometri imeandikwa kama\(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\). Tunaweza kuandika jumla hii kwa kuanzia na muhula wa kwanza\(a_{1}\), na kuendelea\(r\) kuzidisha kwa kupata muda ujao kama:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
Hebu pia kuzidisha pande zote mbili za equation na\(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
Kisha, tunaondoa equations hizi. Tutaona kwamba wakati sisi Ondoa, wote lakini muda wa kwanza wa equation juu na muda wa mwisho wa equation chini Ondoa kwa sifuri.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
Tunazingatia pande zote mbili.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
Ili kupata formula kwa\(S_{n}\), kugawanya pande zote mbili na\((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Jumla,\(S_{n}\), ya\(n\) maneno ya kwanza ya mlolongo wa kijiometri ni
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
wapi\(a_{1}\) muda wa kwanza na\(r\) ni uwiano wa kawaida, na\(r\) si sawa na moja.
Tunatumia fomu hii katika mfano unaofuata ambapo maneno machache ya mlolongo yanapewa. Angalia jumla ya mlolongo wa kijiometri kawaida anapata kubwa sana wakati uwiano wa kawaida ni mkubwa kuliko moja.
Pata jumla ya\(20\) maneno ya kwanza ya mlolongo wa kijiometri\(7, 14, 28, 56, 112, 224, …\)
Suluhisho:
Ili kupata jumla, tutatumia formula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Tunajua\(a_{1}=7\),\(r=2\), na\(n=20\),
Kujua\(a_{1}=7, r=2\), na\(n=20\), tumia formula ya jumla.
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Mbadala katika maadili.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
Kurahisisha.
\(S_{20}=7,340,025\)
Pata jumla ya\(20\) maneno ya kwanza ya mlolongo wa kijiometri\(3, 6, 12, 24, 48, 96, …\)
- Jibu
-
\(3,145,725\)
Pata jumla ya\(20\) maneno ya kwanza ya mlolongo wa kijiometri\(6, 18, 54, 162, 486, 1,458, …\)
- Jibu
-
\(10,460,353,200\)
Katika mfano unaofuata, tunapewa jumla katika maelezo ya muhtasari. Wakati wa kuongeza maneno yote inaweza iwezekanavyo, mara nyingi ni rahisi kutumia formula ili kupata jumla ya\(n\) maneno ya kwanza.
Ili kutumia formula, tunahitaji\(r\). Tunaweza kuipata kwa kuandika maneno machache ya mlolongo na kupata uwiano wao. Chaguo jingine ni kutambua kwamba kwa muhtasari wa muhtasari, mlolongo umeandikwa kwa fomu\(\sum_{i=1}^{k} a(r)^{i}\), ambapo\(r\) ni uwiano wa kawaida.
Pata jumla:\(\sum_{i=1}^{15} 2(3)^{i}\).
Suluhisho:
Ili kupata jumla, tutatumia formula\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\), ambayo inahitaji\(a_{1}\) na\(r\). Tutaandika maneno machache, ili tuweze kupata taarifa zinazohitajika.
 |
|
| Andika maneno machache ya kwanza. | 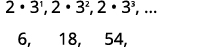 |
| Tambua\(a_{1}\). |  |
| Pata uwiano wa kawaida. |  |
| Kujua\(a_{1}=6\),\(r=3\), na\(n=15\), tumia formula ya jumla. | 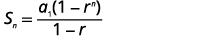 |
| Mbadala katika maadili. | 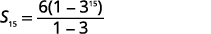 |
| Kurahisisha. | 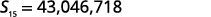 |
Pata jumla:\(\sum_{i=1}^{15} 6(2)^{i}\).
- Jibu
-
\(393,204\)
Pata jumla:\(\sum_{i=1}^{10} 5(2)^{i}\).
- Jibu
-
\(10,230\)
Pata Jumla ya Mfululizo wa Kijiometri usio
Ikiwa tunachukua mlolongo wa kijiometri na kuongeza maneno, tuna jumla inayoitwa mfululizo wa kijiometri. Mfululizo usio na kipimo wa kijiometri ni jumla isiyo na kipimo ambacho muda wake wa kwanza ni\(a_{1}\) na uwiano wa kawaida ni\(r\) na umeandikwa
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
Mfululizo usio na kipimo wa kijiometri ni jumla isiyo na kipimo ambacho muda wake wa kwanza ni\(a_{1}\) na uwiano wa kawaida ni\(r\) na umeandikwa
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
Tunajua jinsi ya kupata jumla ya\(n\) maneno ya kwanza ya mfululizo wa kijiometri kwa kutumia formula,\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). Lakini tunawezaje kupata jumla ya jumla isiyo na kipimo?
Hebu tuangalie mfululizo usio na kipimo wa kijiometri\(3+6+12+24+48+96+….\). Kila neno linapata kubwa na kubwa kwa hivyo inakuwa na maana kwamba jumla ya idadi isiyo na kipimo ya maneno hupata kubwa. Hebu tuangalie kiasi chache cha sehemu ya mfululizo huu. Tunaona\(a_{1}=3\) na\(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
Kama\(n\) anapata kubwa na kubwa, jumla anapata kubwa na kubwa. Hii ni kweli wakati\(|r|≥1\) na tunaita mfululizo tofauti. Hatuwezi kupata jumla ya mfululizo usio wa kijiometri wakati\(|r|≥1\).
Hebu tuangalie mfululizo usio na kipimo wa kijiometri ambao uwiano wa kawaida ni sehemu chini ya moja,
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). Hapa maneno kupata ndogo na ndogo kama\(n\) anapata kubwa. Hebu tuangalie kiasi chache cha mwisho cha mfululizo huu. Tunaona\(a_{1}=\frac{1}{2}\) na\(r=\frac{1}{2}\).
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
Angalia jumla anapata kubwa na kubwa lakini pia anapata karibu na karibu na moja. Wakati\(|r|<1\), maneno\(r^{n}\) hupata ndogo na ndogo. Katika kesi hii, tunaita mfululizo wa mfululizo. Kama\(n\) inakaribia infinity, (anapata kubwa sana),\(r^{n}\) anapata karibu na karibu na sifuri. Katika formula yetu jumla, tunaweza kuchukua nafasi ya\(r^{n}\) na sifuri na kisha sisi kupata formula kwa jumla\(S\), kwa usio mfululizo kijiometri wakati\(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
Fomu hii inatupa jumla ya mlolongo usio na kipimo wa kijiometri. Taarifa\(S\) haina subscript\(n\)\(S_{n}\) kama katika kama sisi si kuongeza idadi ya mwisho ya maneno.
Kwa mfululizo usio wa kijiometri ambao muda wa kwanza ni\(a_{1}\) na uwiano wa kawaida\(r\),
Kama\(|r|<1\), jumla ni
\(S=\frac{a_{1}}{1-r}\)
Ikiwa\(|r|≥1\), mfululizo wa kijiometri usio na kipimo hauna jumla. Tunasema mfululizo hupungua.
Pata jumla ya mfululizo usio wa kijiometri\(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
Suluhisho:
Ili kupata jumla, sisi kwanza tunapaswa kuthibitisha kuwa uwiano wa kawaida\(|r|<1\) na kisha tunaweza kutumia formula ya jumla\(S=\frac{a_{1}}{1-r}\).
Pata uwiano wa kawaida.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
Tambua\(a_{1}\).
\(a_{1}=54\)
Kujua\(a_{1}=54, r=\frac{1}{3}\), tumia formula ya jumla.
\(S=\frac{a_{1}}{1-r}\)
Mbadala katika maadili.
\(S=\frac{54}{1-\frac{1}{3}}\)
Kurahisisha.
\(S=81\)
Jibu:
\(S=80\)
Pata jumla ya mfululizo usio wa kijiometri\(48+24+12+6+3+\frac{3}{2}+\dots\)
- Jibu
-
\(96\)
Pata jumla ya mfululizo usio wa kijiometri\(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- Jibu
-
\(\frac{256}{3}\)
Matumizi ya kuvutia ya mfululizo wa kijiometri usio na kipimo ni kuandika decimal kurudia kama sehemu.
Andika decimal kurudia\(0.5\) kama sehemu.
Suluhisho:
Andika upya\(0.5\) kuonyesha tano kurudia. Tumia thamani ya mahali ili uandike upya hii kama jumla. Hii ni mfululizo usio na kipimo wa kijiometri.
0.5555555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
Pata uwiano wa kawaida.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
Tambua\(a_{1}\)
\(a_{1}=0.5\)
Kujua\(a_{1}=0.5 ,r=0.1\), tumia formula ya jumla.
\(S=\frac{a_{1}}{1-r}\)
Mbadala katika maadili.
\(S=\frac{0.5}{1-0.1}\)
Kurahisisha.
\(S=\frac{0.5}{0.9}\)
Panua nambari na denominator na\(10\).
\(S=\frac{5}{9}\)
Tunaulizwa kupata fomu ya sehemu.
\(0.5 = \frac{5}{9}\)
Andika decimal kurudia\(0.4\) kama sehemu.
- Jibu
-
\(\frac{4}{9}\)
Andika decimal kurudia\(0.8\) kama sehemu.
- Jibu
-
\(\frac{8}{9}\)
Tumia Utaratibu wa Kijiometri na Mfululizo katika Ulimwenguni
Matumizi moja ya utaratibu wa kijiometri inahusiana na matumizi ya watumiaji. Ikiwa marupurupu ya kodi hutolewa kwa kila kaya, athari kwa uchumi ni mara nyingi kiasi cha marupurupu ya mtu binafsi.
Serikali imeamua kutoa marupurupu\(1,000\) ya kodi ya $ kwa kila kaya ili kuchochea uchumi. Takwimu za serikali zinasema kwamba kila kaya itatumia\(80\)% ya marupurupu katika bidhaa na huduma. Wafanyabiashara na watu ambao walifaidika na kuwa\(80\)%\(80\) watatumia% ya yale waliyopata na kadhalika. Matokeo huitwa athari ya kuzidisha. Je, ni matokeo ya jumla ya marupurupu juu ya uchumi?
Suluhisho:
Kila wakati pesa inakwenda katika uchumi,\(80\)% ya hiyo hutumiwa na kisha ni katika uchumi kutumiwa. Tena,\(80\)% ya fedha hizi zinatumika katika uchumi tena. Hali hii inaendelea na hivyo inatuongoza kwenye mfululizo usio na kipimo wa kijiometri.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
Hapa muda wa kwanza ni\(1,000, a_{1}=1000\). Uwiano wa kawaida ni\(0.8, r=0.8\). Tunaweza kutathmini jumla hii tangu\(0.8<1\). Tunatumia formula kwa jumla kwenye mfululizo usio na kipimo wa kijiometri.
\(S=\frac{a_{1}}{1-r}\)
Mbadala katika maadili,\(a_{1}=1,000\) na\(r=0.8\).
\(S=\frac{1,000}{1-0.8}\)
Tathmini.
\(S=5,000\)
Jibu:
Athari ya jumla ya $\(1,000\) iliyopokelewa na kila kaya itakuwa\(5,000\) ukuaji wa $ katika uchumi.
Je, ni athari ya jumla juu ya uchumi wa marupurupu ya kodi ya serikali ya $\(1,000\) kwa kila kaya ili kuchochea uchumi kama kila kaya itatumia\(90\)% ya marupurupu katika bidhaa na huduma?
- Jibu
-
$\(10,000\)
Je, ni athari ya jumla juu ya uchumi wa marupurupu ya kodi ya serikali ya $\(500\) kwa kila kaya ili kuchochea uchumi kama kila kaya itatumia\(85\)% ya marupurupu katika bidhaa na huduma?
- Jibu
-
$\(3,333.33\)
Sisi inaonekana katika formula kiwanja maslahi ambapo mkuu,\(P\), imewekeza kwa kiwango cha riba\(r\), kwa\(t\) miaka. usawa mpya,\(A\), ni\(A=P\left(1+\frac{r}{n}\right)^{n t}\) wakati maslahi ni\(n\) imezungukwa mara mwaka. Fomula hii inatumika wakati mkupuo ilikuwa imewekeza upfront na inatuambia thamani baada ya kipindi fulani wakati.
Annuity ni uwekezaji ambayo ni mlolongo wa amana sawa mara kwa mara. Tutakuwa kuangalia annuities kwamba kulipa riba wakati wa amana. Kama sisi kuendeleza formula kwa thamani ya annuity, sisi ni kwenda basi\(n=1\). Hiyo ina maana kuna amana moja kwa mwaka.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
Tuseme\(P\) dola imewekeza mwishoni mwa kila mwaka. Mwaka mmoja baadaye amana hiyo ni ya thamani ya\(P(1+r)^{1}\) dola, na mwaka mwingine baadaye ni thamani ya\(P(1+r)^{2}\) dola. Baada ya\(t\) miaka, itakuwa na thamani ya\(P(1+r)^{t}\) dola.
| Mwisho wa mwaka\(1\) | Mwisho wa mwaka\(2\) | Mwisho wa mwaka\(3\) | |
|---|---|---|---|
| Kwanza Amana\(P\) @ mwisho wa mwaka\(1\) | \ (1\) ">\(P\) | \ (2\) ">Kiasi\(1\) mwaka baadaye\(P(1+r)^{1}\) | \ (3\) ">Kiasi\(2\) miaka baadaye\(P(1+r)^{2}\) |
| \(2\)Na Amana\(P\) @ mwisho wa mwaka\(2\) | \ (1\) "> | \ (2\) ">\(P\) | \ (3\) ">Kiasi\(1\) mwaka baadaye\(P(1+r)^{1}\) |
| \(3\)rd Amana\(P\) @ mwisho wa mwaka\(3\) | \ (1\) "> | \ (2\) "> | \ (3\) ">\(P\) |
Baada ya miaka mitatu, thamani ya annuity ni
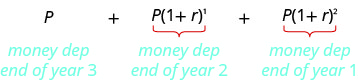
Hii jumla ya masharti ya mlolongo wa kijiometri ambapo muda wa kwanza ni\(P\) na uwiano wa kawaida ni\(1+r\). Sisi badala ya maadili haya katika formula jumla. Kuwa makini, tuna matumizi mawili tofauti ya\(r\). Ya jumla\(r\) ya formula ni uwiano wa kawaida wa mlolongo. Katika kesi hiyo, ndio\(1+r\) ambapo\(r\) ni kiwango cha riba.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
Kumbuka Nguzo yetu ni kwamba amana moja ilitolewa mwishoni mwa kila mwaka.
Tunaweza kukabiliana formula hii kwa\(n\) amana alifanya kwa mwaka na riba ni\(n\) imezungukwa mara mwaka.
Kwa mkuu\(P\), imewekeza mwishoni mwa kipindi compounding, na kiwango cha riba,\(r\), ambayo ni\(n\) imezungukwa mara mwaka, usawa mpya\(A\), baada ya\(t\) miaka, ni
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Wazazi wapya wanaamua kuwekeza $\(100\) kwa mwezi kwa annuity kwa binti yao ya mtoto. Akaunti italipa riba\(5\)% kwa mwaka ambayo imezungukwa kila mwezi. Kiasi gani kitakuwa katika akaunti ya mtoto wakati wa kuzaliwa kwake kumi na nane?
Suluhisho:
Ili kupata formula Annuity\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\),, tunahitaji kutambua\(P, r, n\), na\(t\).
Kutambua\(P\), kiasi imewekeza kila mwezi.
\(P=100\)
Tambua\(r\), kiwango cha riba ya kila mwaka, kwa fomu ya decimal.
\(r=0.05\)
Kutambua\(n\), idadi ya mara amana zitafanywa na maslahi imezungukwa kila mwaka.
\(n=12\)
Tambua\(t\), idadi ya miaka.
\(t=18\)
Kujua\(P=100, r=0.05, n=12\) na\(t=18\), tumia formula ya jumla.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Mbadala katika maadili.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
Tumia calculator kutathmini. Hakikisha kutumia mabano kama inahitajika.
\(A_{t}=34.920 .20\)
Jibu:
Mtoto atakuwa na $\(34,920.20\)
New mababu kuamua kuwekeza $\(200\) kwa mwezi katika annuity kwa mjukuu wao. Akaunti italipa riba\(5\)% kwa mwaka ambayo imezungukwa kila mwezi. Kiasi gani kitakuwa katika akaunti ya mtoto wakati wa kuzaliwa kwake ishirini na moja?
- Jibu
-
$\(88,868.36\)
Arturo alipata kazi yake ya kwanza ya wakati wote baada ya kuhitimu kutoka chuo kikuu akiwa na umri\(27\). Aliamua kuwekeza $\(200\) kwa mwezi katika IRA (annuity). Maslahi juu ya annuity ni\(8\)%, ambayo imezungukwa kila mwezi. Kiasi gani itakuwa katika akaunti ya Arturo wakati anastaafu siku yake ya kuzaliwa sitini na saba?
- Jibu
-
$\(698,201.57\)
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na Utaratibu.
Dhana muhimu
- Muda Mkuu (\(n\)th mrefu) ya Mlolongo wa Kijiometri: Muda wa jumla wa mlolongo wa kijiometri\(a_{1}\) na muda wa kwanza na uwiano wa kawaida\(r\) ni
\(a_{n}=a_{1} r^{n-1}\)
- Jumla ya\(n\) Masharti ya Kwanza ya Mfululizo wa Kijiometri: Jumla,\(S_{n}\), ya\(n\) maneno ya mlolongo wa kijiometri ni
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
ambapo\(a_{1}\) ni muda wa kwanza na\(r\) ni uwiano wa kawaida. Mfululizo wa Kijiometri usio: Mfululizo wa kijiometri usio ni jumla isiyo\(a_{1}\) na kipimo ambao muda wake wa kwanza ni\(r\) na uwiano wa kawaida umeandikwa\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- Jumla ya Infinite Kijiometri Series: Kwa usio kijiometri mfululizo ambao kwanza mrefu ni\(a_{1}\) na uwiano wa kawaida\(r\)\(|r|<1\),
Kama, jumla ni
\(S=\frac{a_{1}}{1-r}\)
Tunasema mfululizo hujiunga.
Ikiwa\(|r|≥1\), mfululizo wa kijiometri usio na kipimo hauna jumla. Tunasema mfululizo hupungua.
- Thamani ya Annuity kwa riba \(n\)imezungukwa Times Mwaka: Kwa mkuu\(P\),, imewekeza mwishoni mwa kipindi compounding, na kiwango cha riba\(r\),, ambayo ni imezungukwa\(n\) mara mwaka, usawa mpya\(A\), baada ya \(t\)miaka, ni
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
faharasa
- annuity
- Annuity ni uwekezaji ambayo ni mlolongo wa amana sawa mara kwa mara.
- uwiano wa kawaida
- Uwiano kati ya maneno mfululizo katika mlolongo wa kijiometri\(r\),, ni, uwiano wa kawaida, ambapo ni\(r\) mkubwa kuliko au sawa na mbili.\(\frac{a_{n}}{a_{n-1}}\)
- mlolongo jiometri
- Mlolongo wa kijiometri ni mlolongo ambapo uwiano kati ya maneno mfululizo daima ni sawa
- mfululizo usio wa kijiometri
- Mfululizo usio wa kijiometri ni mlolongo usio na kipimo wa kijiometri.


