12.3: Utaratibu wa hesabu
- Page ID
- 175683
Mwishoni mwa sehemu hii, utaweza:
- Kuamua kama mlolongo ni hesabu
- Pata neno la jumla (\(n\)neno) la mlolongo wa hesabu
- Pata jumla ya\(n\) masharti ya kwanza ya mlolongo wa hesabu
Kabla ya kuanza, fanya jaribio hili la utayari.
- Tathmini\(4n−1\) kwa integers\(1, 2, 3\), na\(4\).
Ikiwa umekosa tatizo hili, kagua Mfano 1.6. - Tatua mfumo wa equations:\(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\).
Ikiwa umekosa tatizo hili, kagua Mfano 4.9. - Kama\(f(n)=\frac{n}{2}(3 n+5)\), kupata\(f(1)+f(20)\).
Kama amekosa tatizo hili, mapitio Mfano 3.49.
Kuamua kama Mlolongo ni Hesabu
Sehemu ya mwisho ilianzisha utaratibu na sasa tutaangalia aina mbili za utaratibu ambazo kila mmoja ana mali maalum. Katika sehemu hii tutaangalia utaratibu wa hesabu na katika sehemu inayofuata, utaratibu wa kijiometri.
Mlolongo wa hesabu ni mlolongo ambapo tofauti kati ya maneno ya mfululizo ni mara kwa mara. Tofauti kati ya maneno mfululizo katika mlolongo wa hesabu, a_ {n} -a_ {n-1}, ni\(d\), tofauti ya kawaida, kwa\(n\) zaidi ya au sawa na mbili.
Mlolongo wa hesabu ni mlolongo ambapo tofauti kati ya maneno ya mfululizo daima ni sawa.
Tofauti kati ya maneno mfululizo, a_ {n} -a_ {n-1}, ni\(d\), tofauti ya kawaida, kwa\(n\) zaidi ya au sawa na mbili.
Kuamua kama kila mlolongo ni hesabu. Ikiwa ndivyo, onyesha tofauti ya kawaida.
- \(5,9,13,17,21,25, \dots\)
- \(4,9,12,17,20,25, \dots\)
- \(10,3,-4,-11,-18,-25, \dots\)
Suluhisho:
Kuamua kama mlolongo ni hesabu, tunapata tofauti ya maneno ya mfululizo yaliyoonyeshwa.
a.\(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)
Mlolongo ni hesabu. Tofauti ya kawaida ni\(d=4\).
b.\(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)
Mlolongo sio hesabu kama tofauti zote kati ya maneno ya mfululizo si sawa. Hakuna tofauti ya kawaida.
c.\(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)
Jibu:
Mlolongo ni hesabu. Tofauti ya kawaida ni\(d=-7\).
Kuamua kama kila mlolongo ni hesabu. Ikiwa ndivyo, onyesha tofauti ya kawaida.
- \(9,20,31,42,53,64, \dots\)
- \(12,6,0,-6,-12,-18, \dots\)
- \(7,1,10,4,13,7, \dots\)
- Jibu
-
- Mlolongo ni hesabu na tofauti ya kawaida\(d=11\).
- Mlolongo ni hesabu na tofauti ya kawaida\(d=-6\).
- Mlolongo sio hesabu kama tofauti zote kati ya maneno ya mfululizo si sawa.
Kuamua kama kila mlolongo ni hesabu. Ikiwa ndivyo, onyesha tofauti ya kawaida.
- \(-4,4,2,10,8,16, \dots\)
- \(-3,-1,1,3,5,7, \dots\)
- \(7,2,-3,-8,-13,-18, \dots\)
- Jibu
-
- Mlolongo sio hesabu kama tofauti zote kati ya maneno ya mfululizo si sawa.
- Mlolongo ni hesabu na tofauti ya kawaida\(d=2\).
- Mlolongo ni hesabu na tofauti ya kawaida\(d=−5\).
Kama tunajua muda wa kwanza,\(a_{1}\), na tofauti ya kawaida,\(d\), tunaweza kuorodhesha idadi ya mwisho ya suala la mlolongo.
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(5\) na tofauti ya kawaida ni\(d=−6\).
Suluhisho:
Tunaanza na muda wa kwanza na kuongeza tofauti ya kawaida. Kisha sisi kuongeza tofauti ya kawaida kwa matokeo kwamba kupata muda ujao, na kadhalika.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)
Jibu:
Mlolongo ni\(5,-1,-7,-13,-19, \dots\)
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(7\) na tofauti ya kawaida ni\(d=−4\).
- Jibu
-
\(7,3,-1,-5,-9, \dots\)
Andika maneno matano ya kwanza ya mlolongo ambapo muda wa kwanza ni\(11\) na tofauti ya kawaida ni\(d=−8\).
- Jibu
-
\(11,3,-5,-13,-21, \dots\)
Pata Muda Mkuu (\(n\)Muda) wa Mlolongo wa Hesabu
Kama tulivyopata formula kwa muda wa jumla wa mlolongo, tunaweza pia kupata formula kwa muda wa jumla wa mlolongo hesabu.
Hebu tuandike maneno machache ya mlolongo ambapo muda wa kwanza ni\(a_{1}\) na tofauti ya kawaida ni\(d\). Sisi kisha kuangalia kwa mfano.
Tunapotafuta mfano tunaona kwamba kila neno linaanza na\(a_{1}\).
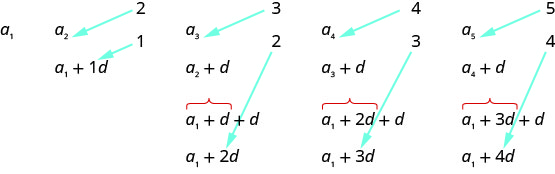
Muda wa kwanza anaongeza\(0d\) kwa\(a_{1}\), muda wa pili anaongeza\(1d\), muhula wa tatu anaongeza\(2d\), muda wa nne anaongeza\(3d\), na muda wa tano anaongeza\(4d\). Idadi ya\(ds\) wale\(a_{1}\) waliongezwa kwa ni moja chini ya idadi ya muda. Hii inatuongoza kwa yafuatayo
\(a_{n}=a_{1}+(n-1) d\)
Neno la jumla la mlolongo wa hesabu na muda wa kwanza\(a_{1}\) na tofauti ya kawaida\(d\) ni
\(a_{n}=a_{1}+(n-1) d\)
Tutatumia formula hii katika mfano unaofuata ili kupata muda wa 15 wa mlolongo.
Kupata kumi na tano mrefu ya mlolongo ambapo muda wa kwanza ni\(3\) na tofauti ya kawaida ni\(6\).
Suluhisho:
\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)
Kupata muda ishirini na saba ya mlolongo ambapo muda wa kwanza ni\(7\) na tofauti ya kawaida ni\(9\).
- Jibu
-
\(241\)
Kupata kumi na nane mrefu ya mlolongo ambapo muda wa kwanza ni\(13\) na tofauti ya kawaida ni\(−7\).
- Jibu
-
\(-106\)
Wakati mwingine hatujui muda wa kwanza na ni lazima tutumie maelezo mengine yaliyopewa ili kuipata kabla ya kupata neno lililoombwa.
Kupata kumi na mbili mrefu ya mlolongo ambapo mrefu saba ni\(10\) na tofauti ya kawaida ni\(−2\). Kutoa formula kwa muda wa jumla.
Suluhisho:
Ili kwanza kupata muda wa kwanza\(a_{1}\), tumia formula na\(a_{7}=10\),\(n=7\), na\(d=−2\). Mbadala katika maadili. Kurahisisha.
\(a_{n}=a_{1}+(n-1) d\)
\(10=a_{1}+(7-1)(-2)\)
\(10=a_{1}+(6)(-2)\)
\(10=a_{1}-12\)
\(a_{1}=22\)
Pata muda wa kumi na mbili\(a_{12}\), kwa kutumia formula na\(a_{1}=22\)\(n=12\),, na\(d=-2\). Mbadala katika maadili. Kurahisisha.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{12}=22+(12-1)(-2)\)
\(a_{12}=22+(11)(-2)\)
\(a_{12}=0\)
Muda wa kumi na mbili wa mlolongo ni\(0, a_{12}=0\)
Ili kupata muda wa jumla, badala ya maadili katika formula.
\(a_{n}=a_{1}+(n-1) d\)
\(a_{n}=22+(n-1)(-2)\)
\(a_{n}=22-2 n+2\)
Jibu:
Neno la jumla ni\(a_{n}=-2 n+24\)
Kupata kumi na moja mrefu ya mlolongo ambapo muda wa tisa ni\(8\) na tofauti ya kawaida ni\(−3\). Kutoa formula kwa muda wa jumla.
- Jibu
-
\(a_{11}=2 .\)Neno la jumla ni\(a_{n}=-3 n+35\)
Pata muda wa kumi na tisa wa mlolongo ambapo muda wa tano ni\(1\) na tofauti ya kawaida\(−4\) ni.Kutoa formula kwa muda wa jumla.
- Jibu
-
\(a_{19}=-55 .\)Neno la jumla ni\(a_{n}=-4 n+21\)
Wakati mwingine taarifa iliyotolewa inatuongoza kwenye equations mbili katika haijulikani mbili. Kisha tunatumia mbinu zetu za kutatua mifumo ya equations ili kupata maadili yanahitajika.
Kupata muda wa kwanza na tofauti ya kawaida ya mlolongo ambapo muda wa tano ni\(19\) na kumi na moja mrefu ni\(37\). Kutoa formula kwa muda wa jumla.
Suluhisho:
Kwa kuwa tunajua maneno mawili, tunaweza kufanya mfumo wa equations kutumia formula kwa muda wa jumla.
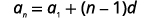 |
|
| Tunajua thamani ya\(a_{5}\) na\(a_{11}\), hivyo tutatumia\(n=5\) na\(n=11\). | 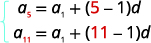 |
Mbadala katika maadili,\(a_{5}=19\) na\(a_{11}=37\). |
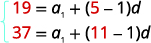 |
| Kurahisisha. | 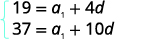 |
| Jitayarishe kuondokana na\(a_{1}\) neno kwa kuzidisha equation ya juu na\(−1\). Ongeza milinganyo. |
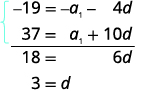 |
| Kubadilisha\(d=3\) nyuma katika equation kwanza. | 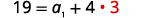 |
| Kutatua kwa\(a_{1}\). |  |
| Tumia formula\(a_{1}=7\) na\(d=3\). | 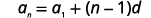 |
| Mbadala katika maadili. | 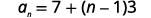 |
| Kurahisisha. | 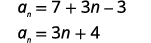 |
| Muda wa kwanza ni\(a_{1}=7\). Tofauti ya kawaida ni\(d=3\). |
|
| Neno la jumla la mlolongo ni\(a_{n}=3n+4\). |
Jibu:
Neno la jumla la mlolongo ni\(a_{n}=3n+4\).
Kupata muda wa kwanza na tofauti ya kawaida ya mlolongo ambapo muda wa nne ni\(17\) na mrefu kumi na tatu ni\(53\). Kutoa formula kwa muda wa jumla.
- Jibu
-
\(a_{1}=5, d=4 .\)Neno la jumla ni\(a_{n}=4 n+1\).
Kupata muda wa kwanza na tofauti ya kawaida ya mlolongo ambapo muda wa tatu ni\(2\) na kumi na mbili mrefu ni\(−25\). Kutoa formula kwa muda wa jumla.
- Jibu
-
\(a_{1}=8, d=-3 .\)Neno la jumla ni\(a_{n}=-3 n+11\).
Pata Jumla ya\(n\) Masharti ya Kwanza ya Mlolongo wa Hesabu
Kama ilivyo kwa utaratibu wa jumla, mara nyingi ni muhimu kupata jumla ya mlolongo wa hesabu. Jumla,\(S_{n}\), ya\(n\) maneno ya kwanza ya mlolongo wowote wa hesabu imeandikwa kama\(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\). Kupata jumla kwa kuongeza tu maneno yote inaweza kuwa tedious. Hivyo tunaweza pia kuendeleza formula kupata jumla ya mlolongo kutumia muda wa kwanza na wa mwisho wa mlolongo.
Tunaweza kuendeleza formula hii mpya kwa kwanza kuandika jumla kwa kuanzia na muhula wa kwanza\(a_{1}\),, na kuendelea kuongeza kupata muda ujao kama:\(d\)
\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).
Tunaweza pia kubadili utaratibu wa maneno na kuandika jumla kwa kuanzia\(a_{n}\) na kuendelea kutoa\(d\) ili kupata muda ujao kama
\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).
Ikiwa tunaongeza maneno haya mawili kwa jumla ya\(n\) masharti ya kwanza ya mlolongo wa hesabu, tunaweza kupata formula kwa jumla ya\(n\) masharti ya kwanza ya mfululizo wowote wa hesabu.
\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)
Kwa sababu kuna\(n\) kiasi cha\((a_{1}+a_{n})\) upande wa kulia wa equation, sisi kuandika upya upande wa kulia kama\(n(a_{1}+a_{n})\).
\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)
Tunagawanya na mbili kutatua\(S_{n}\).
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
Hii inatupa formula ya jumla kwa jumla ya\(n\) masharti ya kwanza ya mlolongo wa hesabu.
Jumla,\(S_{n}\), ya\(n\) masharti ya kwanza ya mlolongo hesabu ni
\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
ambapo\(a_{1}\) ni muda wa kwanza na\(a_{n}\) ni mrefu\(n\) th.
Tunatumia fomu hii katika mfano unaofuata ambapo maneno machache ya mlolongo yanapewa.
Pata jumla ya\(30\) masharti ya kwanza ya mlolongo wa hesabu:\(8, 13, 18, 23, 28, …\)
Suluhisho:
Ili kupata jumla, tutatumia formula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Tunajua\(a_{1}=8, d=5\) na\(n=30\), lakini tunahitaji kupata\(a_{n}\) ili kutumia formula ya jumla.
Pata\(a_{n}\) wapi\(a_{1}=8, d=5\) na\(n=30\). Kurahisisha.
\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)
Kujua\(a_{1}=8, n=30\), na\(a_{30}=153\), tumia fomu ya jumla. Mbadala katika maadili. Kurahisisha. Kurahisisha.
\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)
Pata jumla ya\(30\) masharti ya kwanza ya mlolongo wa hesabu:\(5, 9, 13, 17, 21, …\)
- Jibu
-
\(1,890\)
Pata jumla ya\(30\) masharti ya kwanza ya mlolongo wa hesabu:\(7, 10, 13, 16, 19, …\)
- Jibu
-
\(1,515\)
Katika mfano unaofuata, tunapewa muda wa jumla kwa mlolongo na tunaulizwa kupata jumla ya\(50\) maneno ya kwanza.
Pata jumla ya\(50\) maneno ya kwanza ya mlolongo wa hesabu ambao muda wake ni\(a_{n}=3n−4\).
Suluhisho:
Ili kupata jumla, tutatumia formula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Tunajua\(n=50\), lakini tunahitaji kupata\(a_{1}\) na\(a_{n}\) ili kutumia formula ya jumla.
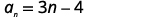 |
|
| Pata\(a_{1}\), kwa kubadilisha\(n=1\). | 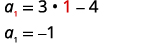 |
| Pata\(a_{n}\) kwa kubadilisha\(n=50\). | 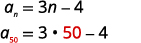 |
| Kurahisisha. | 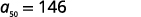 |
| Kujua\(n=50, a_{1}=−1,\) na\(a_{50}=146\) kutumia formula ya jumla. | 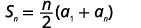 |
| Mbadala katika maadili. | 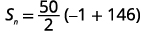 |
| Kurahisisha. | 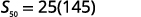 |
| Kurahisisha. | 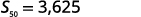 |
Pata jumla ya\(50\) maneno ya kwanza ya mlolongo wa hesabu ambao muda wake ni\(a_{n}=2n−5\).
- Jibu
-
\(2,300\)
Pata jumla ya\(50\) maneno ya kwanza ya mlolongo wa hesabu ambao muda wake ni\(a_{n}=4n+3\).
- Jibu
-
\(5,250\)
Katika mfano unaofuata tunapewa jumla katika maelezo ya muhtasari. Ili kuongeza maneno yote itakuwa ya kuchochea, kwa hiyo tunaondoa habari zinazohitajika kutumia formula ili kupata jumla ya\(n\) maneno ya kwanza.
Pata jumla:\(\sum_{i=1}^{25}(4 i+7)\).
Suluhisho:
Ili kupata jumla, tutatumia formula\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). Tunajua\(n=25\), lakini tunahitaji kupata\(a_{1}\) na\(a_{n}\) ili kutumia formula ya jumla.
| Panua notation ya muhtasari. |
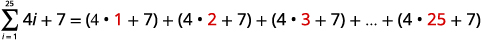
|
| Kurahisisha. |
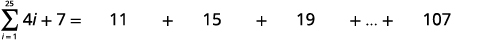
|
| Tambua\(a_{1}\). |  |
| Tambua\(a_{25}\). |

|
| Kujua\(n=25, a_{1}=11\), na\(a_{25} = 107\) kutumia formula ya jumla. |  |
| Mbadala katika maadili. |  |
| Kurahisisha. |  |
| Kurahisisha. |  |
Pata jumla:\(\sum_{i=1}^{30}(6 i-4)\).
- Jibu
-
\(2,670\)
Pata jumla:\(\sum_{i=1}^{35}(5 i-3)\).
- Jibu
-
\(3,045\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na utaratibu wa hesabu
Dhana muhimu
- General Term (\(n\)th mrefu) ya Mlolongo
Hesabu mrefu ya mlolongo hesabu na muda wa kwanza\(a_{1}\) na tofauti ya kawaida\(d\) ni\(a_{n}=a_{1}+(n-1) d\)
- Jumla ya\(n\) Masharti ya Kwanza ya Mlolongo
Hesabu Jumla\(S_{n}\),, ya kwanza\\(n\) suala la mlolongo hesabu, ambapo\(a_{1}\) ni mrefu kwanza na\(a_{n}\) ni\(n\) th mrefu ni\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)
faharasa
- mlolongo wa hesabu
- Mlolongo wa hesabu ni mlolongo ambapo tofauti kati ya maneno ya mfululizo ni mara kwa mara.
- tofauti ya kawaida
- Tofauti kati ya maneno mfululizo katika mlolongo wa hesabu,\(a_{n}−a_{n−1}\), ni\(d\), tofauti ya kawaida, kwa\(n\) zaidi ya au sawa na mbili.


