Skip to main content
Global

Sura ya 11 Mazoezi Mapitio

  1. Last updated
  2. Save as PDF
  • Page ID
    176842

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Sura ya Mapitio ya mazoezi

    Umbali na Midpoint Formula; Mizunguko

    Zoezi\(\PageIndex{1}\) Use the Distance Formula

    Katika mazoezi yafuatayo, tafuta umbali kati ya pointi. Pande zote hadi kumi karibu ikiwa inahitajika.

    1. \((-5,1)\)na\((-1,4)\)
    2. \((-2,5)\)na\((1,5)\)
    3. \((8,2)\)na\((-7,-3)\)
    4. \((1,-4)\)na\((5,-5)\)
    Jibu

    2. \(d=3\)

    4. \(d=\sqrt{17}, d \approx 4.1\)

    Zoezi\(\PageIndex{2}\) Use the Midpoint Formula

    Katika mazoezi yafuatayo, pata midpoint ya makundi ya mstari ambao mwisho wake hutolewa.

    1. \((-2,-6)\)na\((-4,-2)\)
    2. \((3,7)\)na\((5,1)\)
    3. \((-8,-10)\)na\((9,5)\)
    4. \((-3,2)\)na\((6,-9)\)
    Jibu

    2. \((4,4)\)

    4. \(\left(\frac{3}{2},-\frac{7}{2}\right)\)

    Zoezi\(\PageIndex{3}\) Write the Equation of a Circle in Standard Form

    Katika mazoezi yafuatayo, weka fomu ya kawaida ya equation ya mduara na habari iliyotolewa.

    1. Radius ni\(15\) na kituo cha\((0,0)\)
    2. Radius ni\(\sqrt{7}\) na kituo cha\((0,0)\)
    3. Radius ni\(9\) na kituo cha\((-3,5)\)
    4. Radius ni\(7\) na kituo cha\((-2,-5)\)
    5. kituo ni\((3,6)\) na uhakika juu ya mduara ni\((3,-2)\)
    6. kituo ni\((2,2)\) na uhakika juu ya mduara ni\((4,4)\)
    Jibu

    2. \(x^{2}+y^{2}=7\)

    4. \((x+2)^{2}+(y+5)^{2}=49\)

    6. \((x-2)^{2}+(y-2)^{2}=8\)

    Zoezi\(\PageIndex{4}\) Graph a Circle

    Katika mazoezi yafuatayo,

    1. Pata kituo na radius, basi
    2. Grafu kila mduara.
    1. \(2 x^{2}+2 y^{2}=450\)
    2. \(3 x^{2}+3 y^{2}=432\)
    3. \((x+3)^{2}+(y-5)^{2}=81\)
    4. \((x+2)^{2}+(y+5)^{2}=49\)
    5. \(x^{2}+y^{2}-6 x-12 y-19=0\)
    6. \(x^{2}+y^{2}-4 y-60=0\)
    Jibu

    2.

    1. radius:\(12,\) kituo cha:\((0,0)\)
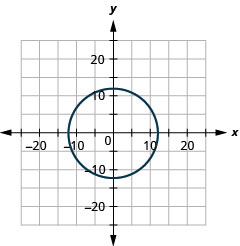
    Takwimu inaonyesha mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 20 hadi 20. Mhimili wa y wa ndege unatoka hasi 15 hadi 15. Katikati ya mduara ni (0, 0) na radius ya mduara ni 12.
    Kielelezo 11.E.1

    4.

    1. radius:\(7,\) kituo cha:\((-2,-5)\)
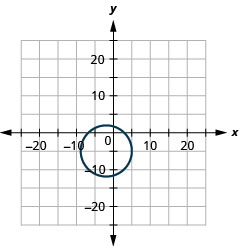
    Takwimu inaonyesha mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 20 hadi 20. Mhimili wa y wa ndege unatoka hasi 15 hadi 15. Katikati ya mduara ni (hasi 2, hasi 5) na radius ya mduara ni 7.
    Kielelezo 11.E.2

    6.

    1. radius:\(8,\) kituo cha:\((0,2)\)
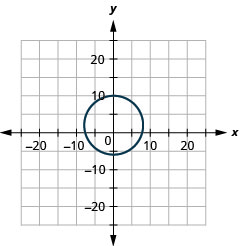
    Takwimu inaonyesha mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 20 hadi 20. Mhimili wa y wa ndege unatoka hasi 15 hadi 15. Katikati ya mduara ni (0, 2) na radius ya mduara ni 8.
    Kielelezo 11.E.3

    Parabola

    Zoezi\(\PageIndex{5}\) Graph Vertical Parabolas

    Katika mazoezi yafuatayo, grafu kila equation kwa kutumia mali zake.

    1. \(y=x^{2}+4 x-3\)
    2. \(y=2 x^{2}+10 x+7\)
    3. \(y=-6 x^{2}+12 x-1\)
    4. \(y=-x^{2}+10 x\)
    Jibu

    2.

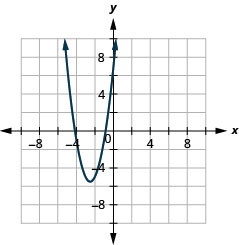
    Takwimu inaonyesha parabola ya juu ya ufunguzi iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 7 hadi 7. Vertex ni (nusu tano hasi, nusu kumi na moja) na parabola hupita kupitia pointi (hasi 4, hasi 1) na (hasi 1, hasi 1).
    Kielelezo 11.E.4

    4.

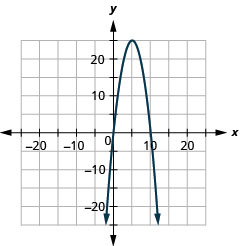
    Takwimu inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 36 hadi 36. Mhimili wa y wa ndege unatoka hasi 26 hadi 26. Vertex ni (5, 25) na parabola hupita kupitia pointi (2, 16) na (8, 16).
    Kielelezo 11.E.5
    Zoezi\(\PageIndex{6}\) Graph Vertical Parabolas

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida, basi
    2. Tumia mali ya fomu ya kawaida ili graph equation.
    1. \(y=x^{2}+4 x+7\)
    2. \(y=2 x^{2}-4 x-2\)
    3. \(y=-3 x^{2}-18 x-29\)
    4. \(y=-x^{2}+12 x-35\)
    Jibu

    2.

    1. \(y=2(x-1)^{2}-4\)
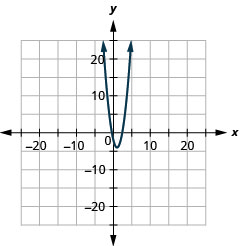
    Takwimu inaonyesha parabola ya juu ya ufunguzi iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 22 hadi 22. Mhimili wa y wa ndege unatoka hasi 16 hadi 16. Vertex ni (1, hasi 4) na parabola hupita kupitia pointi (0, hasi 2) na (2, hasi 2).
    Kielelezo 11.E.6

    4.

    1. \(y=-(x-6)^{2}+1\)
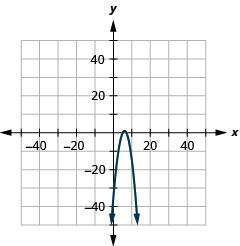
    Takwimu inaonyesha parabola ya kufungua chini iliyopigwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 60 hadi 60. Mhimili wa y wa ndege unatoka hasi 46 hadi 46. Vertex ni (6, 1) na parabola hupita kupitia pointi (5, 0) na (7, 0).
    Kielelezo 11.E.7
    Zoezi\(\PageIndex{7}\) Graph Horizontal Parabolas

    Katika mazoezi yafuatayo, grafu kila equation kwa kutumia mali zake.

    1. \(x=2 y^{2}\)
    2. \(x=2 y^{2}+4 y+6\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(x=-3 y^{2}\)
    Jibu

    2.

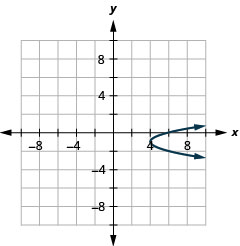
    Takwimu inaonyesha parabola ya ufunguzi wa kulia iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Vertex ni (4, hasi 1) na parabola hupita kupitia pointi (6, 0) na (6, hasi 2).
    Kielelezo 11.E.8

    4.

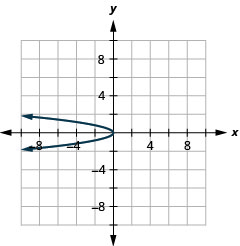
    Takwimu inaonyesha parabola ya ufunguzi wa kushoto iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Vertex ni (0, 0) na parabola hupita kupitia pointi (hasi 3, 1) na (hasi 3, hasi 1).
    Kielelezo 11.E.9
    Zoezi\(\PageIndex{8}\) Graph Horizontal Parabolas

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida, basi
    2. Tumia mali ya fomu ya kawaida ili graph equation.
    1. \(x=4 y^{2}+8 y\)
    2. \(x=y^{2}+4 y+5\)
    3. \(x=-y^{2}-6 y-7\)
    4. \(x=-2 y^{2}+4 y\)
    Jibu

    2.

    1. \(x=(y+2)^{2}+1\)
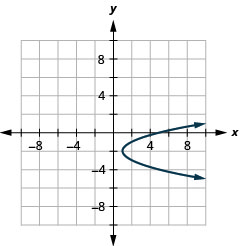
    Takwimu inaonyesha parabola ya ufunguzi wa kulia iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Vertex ni (1, hasi 2) na parabola hupita kupitia pointi (5, 0) na (5, hasi 4).
    Kielelezo 11.E.10

    4.

    1. \(x=-2(y-1)^{2}+2\)
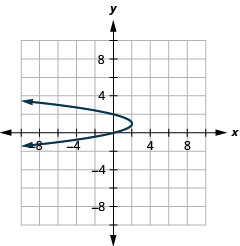
    Takwimu inaonyesha parabola ya ufunguzi wa kushoto iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Vertex ni (2, hasi 3) na parabola hupita kupitia pointi (0, 2) na (0, 0).
    Kielelezo 11.E.11
    Zoezi\(\PageIndex{9}\) Solve Applications with Parabolas

    Katika mazoezi yafuatayo, tengeneza equation ya upinde wa parabolic uliofanywa katika msingi wa daraja iliyoonyeshwa. Kutoa jibu kwa fomu ya kawaida.

    1.

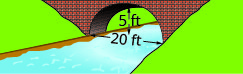
    Takwimu inaonyesha arch parabolic sumu katika msingi wa daraja. Arch ni urefu wa miguu 5 na upana wa futi 20.
    Kielelezo 11.E.12

    2.

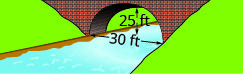
    Takwimu inaonyesha arch parabolic sumu katika msingi wa daraja. Arch ni urefu wa miguu 25 na upana wa futi 30.
    Kielelezo 11.E.13
    Jibu

    2. \(y=-\frac{1}{9} x^{2}+\frac{10}{3} x\)

    duaradufu

    Zoezi\(\PageIndex{10}\) Graph an Ellipse with Center at the Origin

    Katika mazoezi yafuatayo, grafu kila duaradufu.

    1. \(\frac{x^{2}}{36}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{4}+\frac{y^{2}}{81}=1\)
    3. \(49 x^{2}+64 y^{2}=3136\)
    4. \(9 x^{2}+y^{2}=9\)
    Jibu

    2.

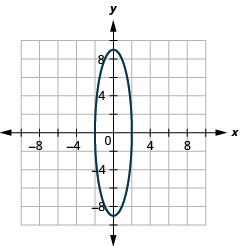
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. duaradufu ina kituo katika (0, 0), wima kuu mhimili, vertices katika (0, pamoja au minus 9), na ushirikiano vertices katika (pamoja au minus 2, 0).
    Kielelezo 11.E.14

    4.

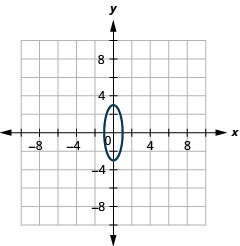
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 9 hadi 9. Mhimili wa y wa ndege unatoka hasi 7 hadi 7. duaradufu ina kituo katika (0, 0), wima kuu mhimili, vertices katika (0, pamoja au minus 3), na ushirikiano vertices katika (pamoja au minus 1, 0).
    Kielelezo 11.E.15
    Zoezi\(\PageIndex{11}\) Find the Equation of an Ellipse with Center at the Origin

    Katika mazoezi yafuatayo, pata equation ya ellipse iliyoonyeshwa kwenye grafu.

    1.

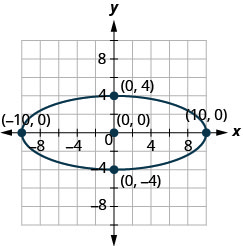
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. duaradufu ina kituo katika (0, 0), usawa mhimili kuu, vertices katika (pamoja au minus 10, 0), na ushirikiano vertices katika (0, pamoja au minus 4).
    Kielelezo 11.E.16

    2.

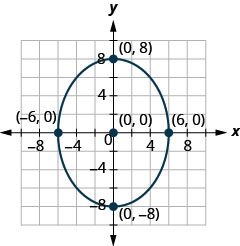
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. duaradufu ina kituo katika (0, 0), wima kuu mhimili, vertices katika (0, pamoja au minus 8), na ushirikiano vertices katika (pamoja au minus 6, 0).
    Kielelezo 11.E.17
    Jibu

    2. \(\frac{x^{2}}{36}+\frac{y^{2}}{64}=1\)

    Zoezi\(\PageIndex{12}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo, grafu kila duaradufu.

    1. \(\frac{(x-1)^{2}}{25}+\frac{(y-6)^{2}}{4}=1\)
    2. \(\frac{(x+4)^{2}}{16}+\frac{(y+1)^{2}}{9}=1\)
    3. \(\frac{(x-5)^{2}}{16}+\frac{(y+3)^{2}}{36}=1\)
    4. \(\frac{(x+3)^{2}}{9}+\frac{(y-2)^{2}}{25}=1\)
    Jibu

    2.

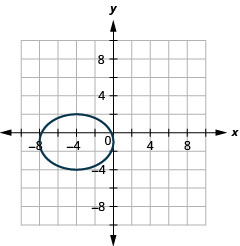
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. duaradufu ina kituo cha (hasi 4, hasi 1), usawa kuu mhimili, vipeo katika (hasi 8, hasi 1) na (0, hasi 1) na ushirikiano wima katika (hasi 4, 2) na (hasi 4, hasi 4).
    Kielelezo 11.E.18

    4.

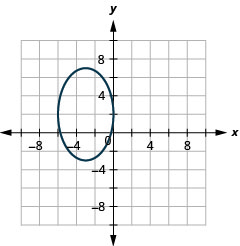
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. duaradufu ina kituo cha (hasi 3, 2), wima kuu mhimili, vipeo katika (hasi 3, 7) na (hasi 3, hasi 3) na ushirikiano wima katika (hasi 6, 2) na (0, 2).
    Kielelezo 11.E.19
    Zoezi\(\PageIndex{13}\) Graph an Ellipse with Center Not at the Origin

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida na
    2. Grafu.
    1. \(x^{2}+y^{2}+12 x+40 y+120=0\)
    2. \(25 x^{2}+4 y^{2}-150 x-56 y+321=0\)
    3. \(25 x^{2}+4 y^{2}+150 x+125=0\)
    4. \(4 x^{2}+9 y^{2}-126 x+405=0\)
    Jibu

    2.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
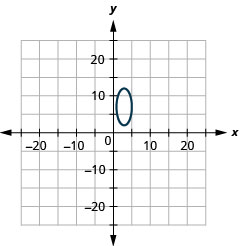
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 18 hadi 18. Mhimili wa y wa ndege unatoka hasi 14 hadi 14. duaradufu ina kituo katika (3, 7), wima kuu mhimili, vipeo katika (3, 2) na (3, 12) na ushirikiano vertices katika (hasi 1, 7) na (5, 7).
    Kielelezo 11.E.20

    4.

    1. \(\frac{x^{2}}{9}+\frac{(y-7)^{2}}{4}=1\)
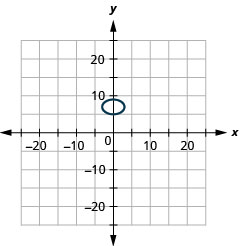
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 15 hadi 15. Mhimili wa y wa ndege unatoka hasi 11 hadi 11. duaradufu ina kituo katika (0, 7), usawa kuu mhimili, vipeo katika (3, 7) na (hasi 3, 7) na ushirikiano vertices katika (0, 5) na (0, 9).
    Kielelezo 11.E.21
    Zoezi\(\PageIndex{14}\) Solve Applications with Ellipses

    Katika mazoezi yafuatayo, andika equation ya ellipse ilivyoelezwa.

    1. Comet huenda katika obiti ya elliptical karibu na jua. Karibu zaidi kimondo kinapata jua ni takriban\(10\) AU na mbali zaidi ni takriban\(90\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya comet.
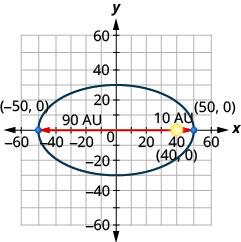
    Takwimu inaonyesha mfano wa obiti ya elliptical kuzunguka jua kwenye ndege ya kuratibu x y. duaradufu ina kituo katika (0, 0), usawa kuu mhimili, alama alama katika (plus au bala 50, 0), jua alama kama foci na kinachoitwa (50, 0), umbali wa karibu zaidi comet ni kutoka jua alama kama 10 U, na mbali zaidi comet ni kutoka jua alama kama 90 A U.
    Kielelezo 11.E.22
    Jibu

    1. Kutatua

    Hyperbolas

    Zoezi\(\PageIndex{15}\) Graph a Hyperbola with Center at \((0,0)\)

    Katika mazoezi yafuatayo, grafu.

    1. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    2. \(\frac{y^{2}}{49}-\frac{x^{2}}{16}=1\)
    3. \(9 y^{2}-16 x^{2}=144\)
    4. \(16 x^{2}-4 y^{2}=64\)
    Jibu

    1.

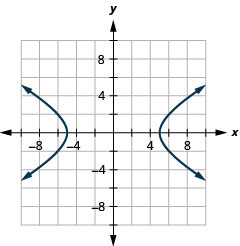
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 12 hadi 12. Mhimili wa y wa ndege unatoka hasi 9 hadi 9. Hyperbola ina kituo cha (0, 0) na matawi ambayo hupita kupitia vertices (pamoja au chini ya 5, 0), na kwamba wazi kushoto na kulia.
    Kielelezo 11.E.23

    3.

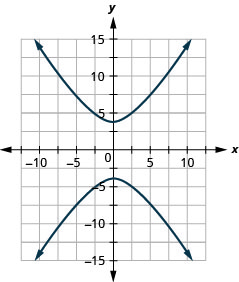
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 19 hadi 19. Mhimili wa y wa ndege unatoka hasi 15 hadi 15. Hyperbola ina kituo cha (0, 0) na matawi ambayo hupita kupitia vertices (0, plus au minus 4), na kwamba kufungua juu na chini.
    Kielelezo 11.E.24
    Zoezi\(\PageIndex{16}\) Graph a Hyperbola with Center at \((h,k)\)

    Katika mazoezi yafuatayo, grafu.

    1. \(\frac{(x+1)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{9}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-2)^{2}}{9}=1\)
    Jibu

    1.

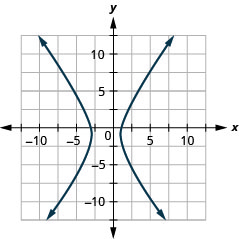
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hyperbola ina kituo cha (hasi 1, hasi 1) na matawi ambayo hupita kupitia vertices (hasi 3, hasi 1) na (1, hasi 1), na kwamba wazi kushoto na kulia.
    Kielelezo 11.E.25

    3.

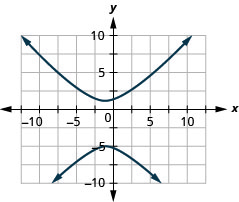
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hyperbola ina kituo cha (hasi 1, hasi 2) na matawi ambayo hupita kupitia vertices (hasi 1, 1) na (hasi 1, hasi 5), na kwamba kufungua na chini.
    Kielelezo 11.E.26
    Zoezi\(\PageIndex{17}\) Graph a Hyperbola with Center at \((h,k)\)

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida na
    2. Grafu.
    1. \(4 x^{2}-16 y^{2}+8 x+96 y-204=0\)
    2. \(16 x^{2}-4 y^{2}-64 x-24 y-36=0\)
    3. \(4 y^{2}-16 x^{2}+32 x-8 y-76=0\)
    4. \(36 y^{2}-16 x^{2}-96 x+216 y-396=0\)
    Jibu

    1.

    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
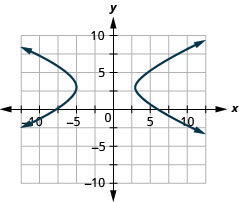
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hyperbola ina kituo cha (hasi 1, 3) na matawi ambayo hupita kupitia vertices (hasi 5, 3) na (3, 3), na kwamba wazi kushoto na kulia.
    Kielelezo 11.E.27

    3.

    1. \(\frac{(y-1)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
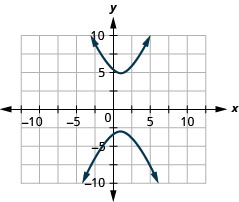
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hyperbola ina kituo cha (1, 1) na matawi ambayo hupita kupitia vertices (1, hasi 3) na (1, 5), na kwamba kufungua juu na chini.
    Kielelezo 11.E.28
    Zoezi\(\PageIndex{18}\) Identify the Graph of Each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    Katika mazoezi yafuatayo, tambua aina ya grafu.

      1. \(16 y^{2}-9 x^{2}-36 x-96 y-36=0\)
      2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      3. \(y=x^{2}-2 x+3\)
      4. \(25 x^{2}+9 y^{2}=225\)
      1. \(x^{2}+y^{2}+4 x-10 y+25=0\)
      2. \(y^{2}-x^{2}-4 y+2 x-6=0\)
      3. \(x=-y^{2}-2 y+3\)
      4. \(16 x^{2}+9 y^{2}=144\)
    Jibu

    1.

    1. Hyperbola
    2. Circle
    3. Parabola
    4. duaradufu

    Kutatua Mifumo ya Equations Nonlinear

    Zoezi\(\PageIndex{19}\) Solve a System of Nonlinear Equations Using Graphing

    Katika mazoezi yafuatayo, tatua mfumo wa equations kwa kutumia graphing.

    1. \(\left\{\begin{array}{l}{3 x^{2}-y=0} \\ {y=2 x-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{y=x^{2}-4} \\ {y=x-4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=169} \\ {x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y=-5}\end{array}\right.\)
    Jibu

    1.

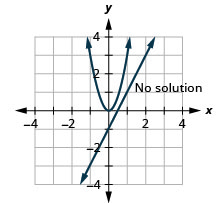
    Takwimu inaonyesha parabola na mstari uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 5 hadi 5. Mhimili wa y wa ndege unatoka hasi 4 hadi 4. Parabola ina vertex saa (0, 0) na kufungua juu. Mstari una mteremko wa 2 na y-intercept saa hasi 1. Parabola na mstari haviingiliani, hivyo mfumo hauna suluhisho.
    Kielelezo 11.E.29

    3.

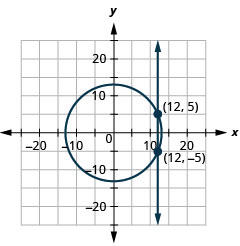
    Takwimu inaonyesha mduara na mstari uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 20 hadi 20. Mhimili wa y wa ndege unatoka hasi 15 hadi 15. Mduara una kituo cha saa (0, 0) na radius ya 13. Mstari ni wima. Mduara na mstari huingiliana kwenye pointi (12, 5) na (12, hasi 5), ambazo zimeandikwa. Suluhisho la mfumo ni (12, 5) na (12, hasi 5)
    Kielelezo 11.E.30
    Zoezi\(\PageIndex{20}\) Solve a System of Nonlinear Equations Using Substitution

    Katika mazoezi yafuatayo, tatua mfumo wa equations kwa kutumia badala.

    1. \(\left\{\begin{array}{l}{y=x^{2}+3} \\ {y=-2 x+2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x-y=4}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{9 x^{2}+4 y^{2}=36} \\ {y-x=5}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=4} \\ {2 x-y=1}\end{array}\right.\)
    Jibu

    1. \((-1,4)\)

    3. Hakuna ufumbuzi

    Zoezi\(\PageIndex{21}\) Solve a System of Nonlinear Equations Using Elimination

    Katika mazoezi yafuatayo, tatua mfumo wa equations kwa kutumia kuondoa.

    1. \(\left\{\begin{array}{l}{x^{2}+y^{2}=16} \\ {x^{2}-2 y-1=0}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}-y^{2}=5} \\ {-2 x^{2}-3 y^{2}=-30}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{4 x^{2}+9 y^{2}=36} \\ {3 y^{2}-4 x=12}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{x^{2}+y^{2}=14} \\ {x^{2}-y^{2}=16}\end{array}\right.\)
    Jibu

    1. \((-\sqrt{7}, 3),(\sqrt{7}, 3)\)

    3. \((-3,0),(0,-2),(0,2)\)

    Zoezi\(\PageIndex{22}\) Use a System of Nonlinear Equations to Solve Applications

    Katika mazoezi yafuatayo, tatua tatizo kwa kutumia mfumo wa equations.

    1. Jumla ya mraba ya namba mbili ni\(25\). Tofauti ya idadi ni\(1\). Kupata idadi.
    2. Tofauti ya mraba wa namba mbili ni\(45\). Tofauti ya mraba wa namba ya kwanza na mara mbili mraba wa namba ya pili ni\(9\). Kupata idadi.
    3. Mzunguko wa mstatili ni\(58\) mita na eneo lake ni mita za\(210\) mraba. Pata urefu na upana wa mstatili.
    4. Colton alinunua microwave kubwa kwa jikoni yake. Ulalo wa mbele wa microwave hupima\(34\) inchi. Mbele pia ina eneo la inchi za\(480\) mraba. Urefu na upana wa microwave ni nini?
    Jibu

    1. \(-3\)na\(-4\) au\(4\) na\(3\)

    3. Ikiwa urefu ni\(14\) inchi, upana ni\(15\) inchi. Ikiwa urefu ni\(15\) inchi, upana ni\(14\) inchi.

    Mazoezi mtihani

    Zoezi\(\PageIndex{23}\)

    Katika mazoezi yafuatayo, tafuta umbali kati ya pointi na katikati ya sehemu ya mstari na mwisho uliopewa. Pande zote hadi kumi karibu kama inahitajika.

    1. \((-4,-3)\)na\((-10,-11)\)
    2. \((6,8)\)na\((-5,-3)\)
    Jibu

    1. umbali:\(10,\) midpoint:\((-7,-7)\)

    Zoezi\(\PageIndex{24}\)

    Katika mazoezi yafuatayo, weka fomu ya kawaida ya equation ya mduara na habari iliyotolewa.

    1. Radius ni\(11\) na kituo cha\((0,0)\)
    2. Radius ni\(12\) na kituo cha\((10,-2)\)
    3. kituo ni\((-2,3)\) na uhakika juu ya mduara ni\((2,-3)\)
    4. Kupata equation ya duaradufu inavyoonekana katika grafu.
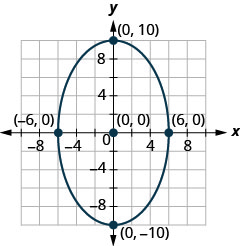
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. duaradufu ina kituo katika (0, 0), wima kuu mhimili, vertices katika (0, pamoja au minus 10), na ushirikiano vertices katika (pamoja au minus 6, 0).
    Kielelezo 11.E.31
    Jibu

    1. \(x^{2}+y^{2}=121\)

    3. \((x+2)^{2}+(y-3)^{2}=52\)

    Zoezi\(\PageIndex{25}\)

    Katika mazoezi yafuatayo,

    1. Kutambua aina ya grafu ya kila equation kama mduara, parabola, duaradufu, au hyperbola, na
    2. Grafu equation.
    1. \(4 x^{2}+49 y^{2}=196\)
    2. \(y=3(x-2)^{2}-2\)
    3. \(3 x^{2}+3 y^{2}=27\)
    4. \(\frac{y^{2}}{100}-\frac{x^{2}}{36}=1\)
    5. \(\frac{x^{2}}{16}+\frac{y^{2}}{81}=1\)
    6. \(x=2 y^{2}+10 y+7\)
    7. \(64 x^{2}-9 y^{2}=576\)
    Jibu

    1.

    1. duaradufu
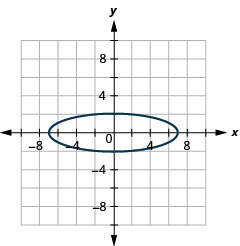
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. duaradufu ina kituo katika (0, 0), usawa mhimili kuu, vertices katika (pamoja au minus 7, 0) na ushirikiano vertices katika (0, pamoja au minus 2).
    Kielelezo 11.E.32

    3.

    1. Circle
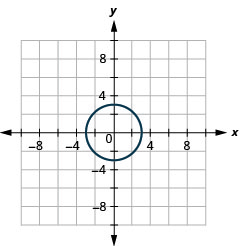
    Takwimu inaonyesha mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Mduara wa parabola una kituo cha (0, 0) na radius ya 3.
    Kielelezo 11.E.33

    5.

    1. duaradufu
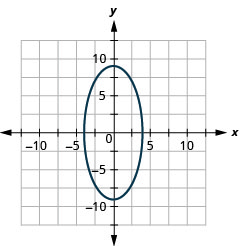
    Takwimu inaonyesha duaradufu iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. duaradufu ina kituo katika (0, 0), wima kuu mhimili, vertices katika (0, pamoja au minus 9) na ushirikiano vertices katika (pamoja au minus 4, 0).
    Kielelezo 11.E.34

    7.

    1. Hyperbola
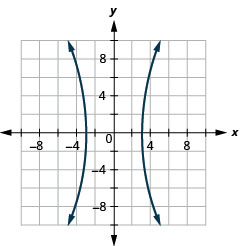
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 10 hadi 10. Mhimili wa y wa ndege unatoka hasi 8 hadi 8. Hyperbola ina kituo cha (0, 0) na matawi ambayo hupita kupitia vertices (pamoja au chini ya 3, 0) na kwamba wazi kushoto na kulia.
    Kielelezo 11.E.35
    Zoezi\(\PageIndex{26}\)

    Katika mazoezi yafuatayo,

    1. Tambua aina ya grafu ya kila equation kama mduara, parabola, duaradufu, au hyperbola,
    2. Andika equation katika fomu ya kawaida, na
    3. Grafu equation.
    1. \(25 x^{2}+64 y^{2}+200 x-256 y-944=0\)
    2. \(x^{2}+y^{2}+10 x+6 y+30=0\)
    3. \(x=-y^{2}+2 y-4\)
    4. \(9 x^{2}-25 y^{2}-36 x-50 y-214=0\)
    5. \(y=x^{2}+6 x+8\)
    6. Tatua mfumo usio wa kawaida wa equations kwa kuchora:\(\left\{\begin{array}{l}{3 y^{2}-x=0} \\ {y=-2 x-1}\end{array}\right.\).
    7. Tatua mfumo usio wa kawaida wa equations kwa kutumia mbadala:\(\left\{\begin{array}{l}{x^{2}+y^{2}=8} \\ {y=-x-4}\end{array}\right.\).
    8. Tatua mfumo usio wa kawaida wa equations kwa kutumia kuondoa:\(\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {2 x^{2}-9 y^{2}=18}\end{array}\right.\)
    9. Kujenga equation ya upinde parabolic sumu katika msingi wa daraja inavyoonekana. Kutoa jibu kwa\(y=a x^{2}+b x+c\) fomu.
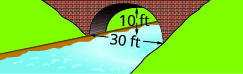
    Takwimu inaonyesha arch parabolic sumu katika msingi wa daraja. Arch ni urefu wa miguu 10 na upana wa futi 30.
    Kielelezo 11.E.36

    10. Comet huenda katika obiti ya elliptical karibu na jua. Karibu zaidi kimondo kinapata jua ni takriban\(20\) AU na mbali zaidi ni takriban\(70\) AU. Jua ni moja ya foci ya obiti ya elliptical. Kuruhusu kituo cha ellipse katika asili na kuandika axes katika AU, obiti itaonekana kama takwimu hapa chini. Tumia grafu kuandika equation kwa obiti elliptical ya comet.

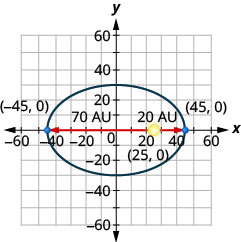
    Takwimu inaonyesha mfano wa obiti ya elliptical kuzunguka jua kwenye ndege ya kuratibu x y. duaradufu ina kituo katika (0, 0), usawa kuu mhimili, alama alama katika (pamoja au bala 45, 0), jua alama kama foci na kinachoitwa (25, 0), umbali wa karibu zaidi comet ni kutoka jua alama 20 U, na mbali zaidi comet ni kutoka jua alama 70 A U.
    Kielelezo 11.E.37

    11. Jumla ya namba mbili ni\(22\) na bidhaa ni\(−240\). Kupata idadi.

    12. Kwa siku yake ya kuzaliwa, babu na babu za Olive walinunua TV mpya ya widescreen. Kabla ya kufungua yeye anataka kuhakikisha kuwa inafaa kituo chake cha burudani. TV ni\(55\)”. Ukubwa wa TV hupimwa kwenye diagonal ya skrini na widescreen ina urefu ambao ni mkubwa kuliko upana. Skrini pia ina eneo la inchi za\(1452\) mraba. Kituo chake cha burudani kina kuingiza kwa TV yenye urefu wa\(50\) inchi na upana wa\(40\) inchi. Urefu na upana wa skrini ya TV ni nini na itafaa kituo cha burudani cha Olive?

    Jibu

    2.

    1. Circle
    2. \((x+5)^{2}+(y+3)^{2}=4\)
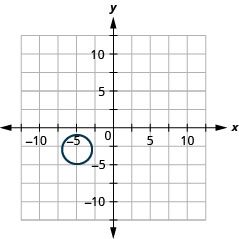
    Takwimu inaonyesha mduara uliowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Mduara una kituo cha (hasi 5, hasi 3) na radius 2.
    Kielelezo 11.E.38

    4.

    1. Hyperbola
    2. \(\frac{(x-2)^{2}}{25}-\frac{(y+1)^{2}}{9}=1\)
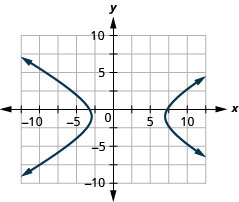
    Takwimu inaonyesha hyperbola iliyowekwa kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 14 hadi 14. Mhimili wa y wa ndege huendesha kutoka hasi 10 hadi 10. Hyperbola ina kituo cha (2, hasi 1) na matawi ambayo hupita kupitia vertices (hasi 3, hasi 1) na (7, hasi 1) ambayo hufungua kushoto na kulia.
    Kielelezo 11.E.39

    6. Hakuna ufumbuzi

    8. \((0,-3),(0,3)\)

    10. \(\frac{x^{2}}{2025}+\frac{y^{2}}{1400}=1\)

    12. Urefu ni\(44\) inchi na upana ni\(33\) inchi. TV itafaa kituo cha burudani cha Olive.

    faharasa

    mfumo wa equations isiyo ya kawaida
    Mfumo wa milinganyo isiyo ya kawaida ni mfumo ambapo angalau moja ya equations si linear.