11.2: Umbali na Midpoint Formula na Miduara
- Page ID
- 176854
Mwishoni mwa sehemu hii, utaweza:
- Tumia Mfumo wa Umbali
- Tumia Mfumo wa Midpoint
- Andika equation ya mduara katika fomu ya kawaida
- Grafu mduara
Kabla ya kuanza, fanya jaribio hili la utayari.
- Pata urefu wa hypotenuse ya pembetatu ya kulia ambayo miguu yake ni\(12\) na\(16\) inchi.
Kama amekosa tatizo hili, mapitio Mfano 2.34. - Sababu:\(x^{2}-18 x+81\).
Kama amekosa tatizo hili, mapitio Mfano 6.24. - Tatua kwa kukamilisha mraba:\(x^{2}-12 x-12=0\).
Kama amekosa tatizo hili, mapitio Mfano 9.22.
Katika sura hii tutaangalia sehemu za conic, ambazo huitwa conics, na mali zao. conics ni curves kwamba matokeo ya ndege intersecting mara mbili koni - mbegu mbili kuwekwa hatua kwa uhakika. Kila nusu ya koni mbili inaitwa nappe.
Kuna nne conics-mduara, parabola, duaradufu, na hyperbola. Takwimu inayofuata inaonyesha jinsi ndege inayoingiliana na matokeo ya koni mara mbili katika kila safu.
Kila moja ya curves ina maombi mengi yanayoathiri maisha yako ya kila siku, kutoka simu yako ya mkononi kwa acoustics na mifumo urambazaji. Katika sehemu hii tutaangalia mali ya mduara.
Tumia Mfumo wa Umbali
Tumetumia Theorem ya Pythagorean kupata urefu wa pande za pembetatu sahihi. Hapa tutatumia theorem hii tena kupata umbali kwenye mfumo wa kuratibu mstatili. Kwa kutafuta umbali kwenye mfumo wa kuratibu mstatili, tunaweza kufanya uhusiano kati ya jiometri ya conic na algebra-ambayo inafungua ulimwengu wa fursa za maombi.
Hatua yetu ya kwanza ni kuendeleza formula ili kupata umbali kati ya pointi kwenye mfumo wa kuratibu mstatili. Tutapanga pointi na kujenga pembetatu sahihi kama tulivyofanya wakati tulipopata mteremko katika Grafu na Kazi. Sisi kisha kuchukua hatua moja zaidi na kutumia Theorem Pythagorean kupata urefu wa hypotenuse ya pembetatu-ambayo ni umbali kati ya pointi.
Tumia mfumo wa kuratibu mstatili ili kupata umbali kati ya pointi\((6,4)\) na\((2,1)\).
Suluhisho
| Plot pointi mbili. Unganisha pointi mbili na mstari. Chora pembetatu sahihi kama ungeenda kupata mteremko. |
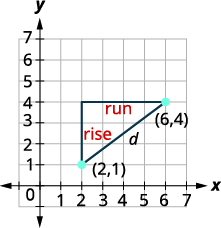
|
| Pata urefu wa kila mguu. |
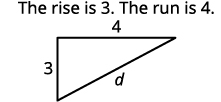
|
| Tumia Theorem ya Pythagorean kupata\(d\), umbali kati ya pointi mbili. | \(a^{2}+b^{2}=c^{2}\) |
| Mbadala katika maadili. | \(3^{2}+4^{2}=d^{2}\) |
| Kurahisisha. | \(9+16=d^{2}\) |
| \(25=d^{2}\) | |
| Tumia Mizizi ya Mizizi ya Mraba. | \(d=5\quad\cancel{d=-5}\) |
| Tangu umbali,\(d\) ni chanya, tunaweza kuondoa\(d=-5\). | Umbali kati ya pointi\((6,4)\) na\((2,1)\) ni\(5\). |
Tumia mfumo wa kuratibu mstatili ili kupata umbali kati ya pointi\((6,1)\) na\((2,-2)\).
- Jibu
-
\(d=5\)
Tumia mfumo wa kuratibu mstatili ili kupata umbali kati ya pointi\((5,3)\) na\((-3,-3)\).
- Jibu
-
\(d=10\)
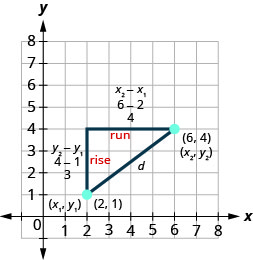
Njia tuliyotumia katika mfano wa mwisho inatuongoza kwenye fomu ili kupata umbali kati ya pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\).
Tulipopata urefu wa mguu usio na usawa tuliondoa\(6−2\) ambayo ni\(x_{2}-x_{1}\).
Tulipopata urefu wa mguu wa wima tuliondoa\(4−1\) ambayo ni\(y_{2}-y_{1}\).
Kama pembetatu alikuwa katika nafasi tofauti, tunaweza kuwa subtracted\(x_{1}-x_{2}\) au\(y_{1}-y_{2}\). Maneno\(x_{2}-x_{1}\) na\(x_{1}-x_{2}\) hutofautiana tu katika ishara ya nambari inayosababisha. Ili kupata thamani chanya tangu umbali ni chanya- tunaweza kutumia thamani kamili. Hivyo kuzalisha tutasema\(\left|x_{2}-x_{1}\right|\) na\(\left|y_{2}-y_{1}\right|\).
Katika Theorem ya Pythagorean, tunabadilisha maneno ya jumla\(\left|x_{2}-x_{1}\right|\) na\(\left|y_{2}-y_{1}\right|\) badala ya namba.
\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)
Hii ni Mfumo wa Umbali tunayotumia ili kupata umbali\(d\) kati ya pointi mbili\((x_{1},y_{1})\) na\((x_{2}, y_{2})\).
Umbali formula
Umbali\(d\) kati ya pointi mbili\((x_{1},y_{1})\) na\((x_{2}, y_{2})\) ni
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((-5,-3)\) na\((7,2)\).
Suluhisho:
Andika Mfumo wa Umbali.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Weka alama,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\),\(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) na mbadala.
\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
Kurahisisha.
\(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
Jibu:
\(d=13\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((-4,-5)\) na\((5,7)\).
- Jibu
-
\(d=15\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((-2,-5)\) na\((-14,-10)\).
- Jibu
-
\(d=13\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((10,−4)\) na\((−1,5)\). Andika jibu kwa fomu halisi na kisha upate makadirio ya decimal, iliyozunguka hadi kumi ya karibu ikiwa inahitajika.
Suluhisho:
Andika Mfumo wa Umbali.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Weka alama,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\),\(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) na mbadala.
\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)
Kurahisisha.
\(d=\sqrt{(-11)^{2}+9^{2}}\)
\(d=\sqrt{121+81}\)
\(d=\sqrt{202}\)
Kwa kuwa\(202\) si mraba kamili, tunaweza kuondoka jibu katika fomu halisi au kupata makadirio decimal.
\(d=\sqrt{202}\)
au
\(d \approx 14.2\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((−4,−5)\) na\((3,4)\). Andika jibu kwa fomu halisi na kisha upate makadirio ya decimal, iliyozunguka hadi kumi ya karibu ikiwa inahitajika.
- Jibu
-
\(d=\sqrt{130}, d \approx 11.4\)
Tumia Mfumo wa Umbali ili kupata umbali kati ya pointi\((−2,−5)\) na\((−3,−4)\). Andika jibu kwa fomu halisi na kisha upate makadirio ya decimal, iliyozunguka hadi kumi ya karibu ikiwa inahitajika.
- Jibu
-
\(d=\sqrt{2}, d \approx 1.4\)
Tumia Mfumo wa Midpoint
Mara nyingi ni muhimu kuwa na uwezo wa kupata midpoint ya sehemu. Kwa mfano, ikiwa una mwisho wa kipenyo cha mduara, unaweza kutaka kupata katikati ya mduara ambayo ni midpoint ya kipenyo. Ili kupata midpoint ya sehemu ya mstari, tunapata wastani wa\(x\) -kuratibu na wastani wa\(y\) -kuratibu za mwisho.
midpoint formula
Midpoint ya sehemu ya mstari ambao mwisho wake ni pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\) ni
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Ili kupata midpoint ya sehemu ya mstari, tunapata wastani wa\(x\) -kuratibu na wastani wa\(y\) -kuratibu za mwisho.
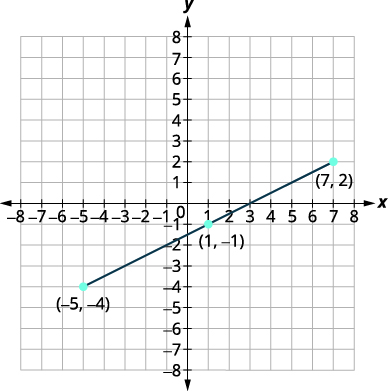
Tumia Mfumo wa Midpoint ili kupata midpoint ya makundi ya mstari ambao mwisho wake ni\((−5,−4)\) na\((7,2)\). Panda mwisho wa mwisho na midpoint kwenye mfumo wa kuratibu mstatili.
Suluhisho:
| Andika Mfumo wa Midpoint. | \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) |
| Lebo pointi,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-4}\end{array}\right), \left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) na mbadala. | \(\left(\frac{-5+7}{2}, \frac{-4+2}{2}\right)\) |
| Kurahisisha. | \(\left(\frac{2}{2}, \frac{-2}{2}\right)\) |
|
\((1,-1)\) Midpoint ya sehemu ni hatua \((1,-1)\). |
|
| Plot endpoints na midpoint. |
|
Tumia Mfumo wa Midpoint ili kupata midpoint ya makundi ya mstari ambao mwisho wake ni\((−3,−5)\) na\((5,7)\). Panda mwisho wa mwisho na midpoint kwenye mfumo wa kuratibu mstatili.
- Jibu
-
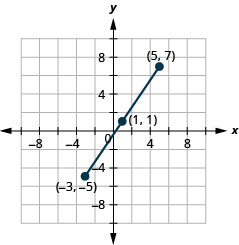
Kielelezo 11.1.7
Tumia Mfumo wa Midpoint ili kupata midpoint ya makundi ya mstari ambao mwisho wake ni\((−2,−5)\) na\((6,−1)\). Panda mwisho wa mwisho na midpoint kwenye mfumo wa kuratibu mstatili.
- Jibu
-
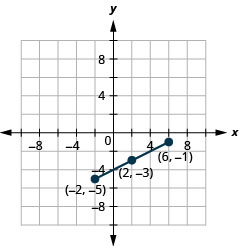
Kielelezo 11.1.8
Mfumo wa Umbali na Mfumo wa Midpoint hutegemea pointi mbili,\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\). Ni rahisi kuchanganya ambayo formula inahitaji kuongeza na ambayo huondoa kuratibu. Kama tunakumbuka ambapo formula kuja kutoka, ni inaweza kuwa rahisi kukumbuka formula.
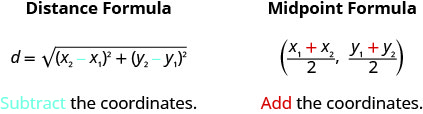
Andika Ulinganisho wa Mzunguko katika Fomu ya Kiwango
Kama tulivyosema, lengo letu ni kuunganisha jiometri ya conic na algebra. Kwa kutumia ndege ya kuratibu, tunaweza kufanya hivyo kwa urahisi.
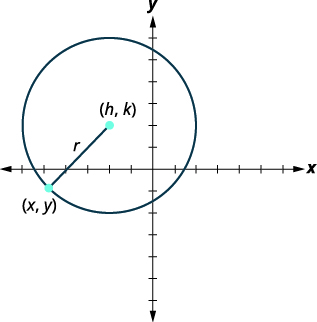
Sisi kufafanua mduara kama pointi zote katika ndege ambayo ni umbali fasta kutoka hatua fulani katika ndege. Hatua iliyotolewa inaitwa kituo,\((h,k)\), na umbali uliowekwa huitwa radius,\(r\), ya mduara.
Mduara ni pointi zote katika ndege ambayo ni umbali fasta kutoka hatua fulani katika ndege. Hatua iliyotolewa inaitwa kituo,\((h,k)\), na umbali uliowekwa huitwa radius,\(r\), ya mduara.
Tunaangalia mduara katika mfumo wa kuratibu mstatili. Radius ni umbali kutoka katikati,\((h,k)\), kwa uhakika juu ya mduara,\((x,y)\). |
|
| Kupata equation ya mduara, tunaweza kutumia formula umbali na pointi\((h,k)\),\((x,y)\) na umbali,\(r\). |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Badilisha maadili. | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| Square pande zote mbili. | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
Hii ni fomu ya kawaida ya equation ya mduara na kituo,\((h,k)\), na radius,\(r\).
Aina ya kiwango cha equation ya mduara na kituo,\((h,k)\), na radius,\(r\), ni
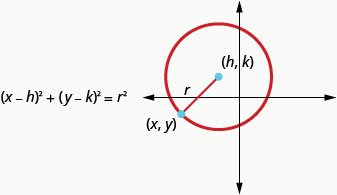
Andika fomu ya kawaida ya equation ya mduara na radius\(3\) na kituo\((0,0)\).
Suluhisho:
| Tumia fomu ya kawaida ya equation ya mduara | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Mbadala katika maadili\(r=3, h=0\), na\(k=0\). | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
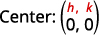 |
|
| Kurahisisha. | \(x^{2}+y^{2}=9\) |
Andika fomu ya kawaida ya equation ya mduara na radius ya\(6\) na katikati\((0,0)\).
- Jibu
-
\(x^{2}+y^{2}=36\)
Andika fomu ya kawaida ya equation ya mduara na radius ya\(8\) na katikati\((0,0)\).
- Jibu
-
\(x^{2}+y^{2}=64\)
Katika mfano wa mwisho, kituo hicho kilikuwa\((0,0)\). Angalia nini kilichotokea kwa equation. Wakati wowote kituo hicho\((0,0)\), fomu ya kawaida inakuwa\(x^{2}+y^{2}=r^{2}\).
Andika fomu ya kawaida ya equation ya mduara na radius\(2\) na kituo\((−1,3)\).
Suluhisho:
| Tumia fomu ya kawaida ya equation ya mduara. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Mbadala katika maadili. | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
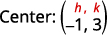 |
|
| Kurahisisha. | \((x+1)^{2}+(y-3)^{2}=4\) |
Andika fomu ya kawaida ya equation ya mduara na radius ya\(7\) na katikati\((2,−4)\).
- Jibu
-
\((x-2)^{2}+(y+4)^{2}=49\)
Andika fomu ya kawaida ya equation ya mduara na radius ya\(9\) na katikati\((−3,−5)\).
- Jibu
-
\((x+3)^{2}+(y+5)^{2}=81\)
Katika mfano unaofuata, radius haipatikani. Ili kuhesabu radius, tunatumia Mfumo wa Umbali na pointi mbili zilizopewa.
Andika fomu ya kawaida ya equation ya mduara na kituo\((2,4)\) ambacho pia kina uhakika\((−2,1)\).
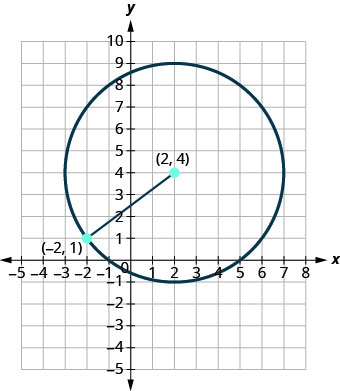
Suluhisho:
Radi ni umbali kutoka katikati hadi hatua yoyote kwenye mduara ili tuweze kutumia formula ya umbali ili kuihesabu. Tutatumia kituo\((2,4)\) na uhakika\((−2,1)\)
Tumia Mfumo wa Umbali ili kupata radius.
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Badilisha maadili. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)
\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)
Kurahisisha.
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(r=\sqrt{16+9}\)
\(r=\sqrt{25}\)
\(r=5\)
Sasa kwa kuwa tunajua Radius\(r=5\),, na kituo\((2,4)\), tunaweza kutumia fomu ya kiwango cha equation ya mduara kupata equation.
Tumia fomu ya kawaida ya equation ya mduara.
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
Mbadala katika maadili.
\((x-2)^{2}+(y-4)^{2}=5^{2}\)
Kurahisisha.
\((x-2)^{2}+(y-4)^{2}=25\)
Andika fomu ya kawaida ya equation ya mduara na kituo\((2,1)\) ambacho pia kina uhakika\((−2,−2)\).
- Jibu
-
\((x-2)^{2}+(y-1)^{2}=25\)
Andika fomu ya kawaida ya equation ya mduara na kituo\((7,1)\) ambacho pia kina uhakika\((−1,−5)\).
- Jibu
-
\((x-7)^{2}+(y-1)^{2}=100\)
Grafu ya Mzunguko
Equation yoyote ya fomu\((x-h)^{2}+(y-k)^{2}=r^{2}\) ni fomu ya kawaida ya equation ya mduara na kituo,\((h,k)\), na radius,\(r\). Tunaweza kisha grafu mduara kwenye mfumo wa kuratibu mstatili.
Kumbuka kuwa fomu ya kawaida inatoa wito wa kuondoa kutoka\(x\) na\(y\). Katika mfano unaofuata, equation ina\(x+2\), hivyo tunahitaji kuandika upya kuongeza kama kutoa ya hasi.
Pata kituo na radius, kisha graph mduara:\((x+2)^{2}+(y-1)^{2}=9\).
Suluhisho:
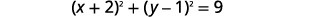 |
|
|
Tumia fomu ya kawaida ya equation ya mduara. Tambua kituo,\((h,k)\) na radius,\(r\). |
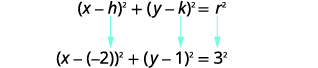 |
| Kituo:\((-2,1)\) radius:\(3\) | |
| Grafu mduara. | 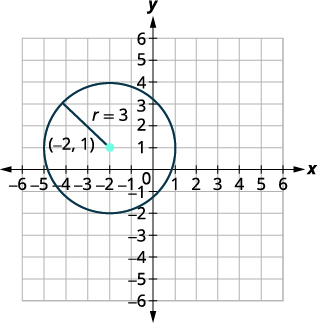 |
- Pata kituo na radius, basi
- Grafu mduara:\((x-3)^{2}+(y+4)^{2}=4\).
- Jibu
-
- mduara ni katikati katika\((3,-4)\) na radius ya\(2\).
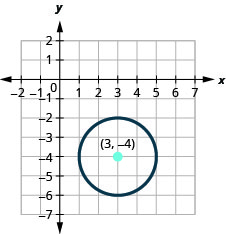
Kielelezo 11.1.19
- Pata kituo na radius, basi
- Grafu mduara:\((x-3)^{2}+(y-1)^{2}=16\).
- Jibu
-
- mduara ni katikati katika\((3,1)\) na radius ya\(4\).
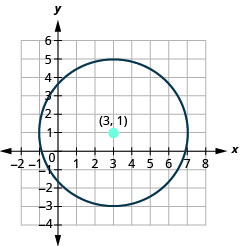
Kielelezo 11.1.20
Ili kupata kituo na radius, lazima tuandike equation katika fomu ya kawaida. Katika mfano unaofuata, ni lazima kwanza kupata mgawo\(x^{2}, y^{2}\) wa kuwa moja.
Pata kituo na radius na kisha graph mduara,\(4 x^{2}+4 y^{2}=64\).
Suluhisho:
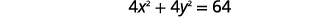 |
|
| Gawanya kila upande\(4\). | 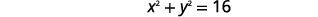 |
| Tumia fomu ya kawaida ya equation ya mduara. Tambua kituo,\((h,k)\) na radius,\(r\). |
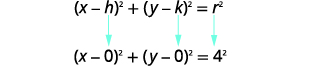 |
| Kituo:\((0,0)\) radius:\(4\) | |
| Grafu mduara. | 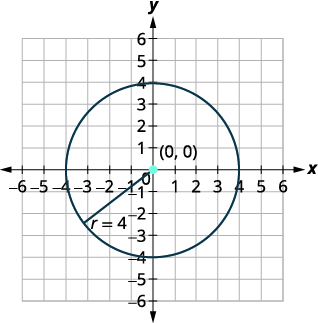 |
- Pata kituo na radius, basi
- Grafu mduara:\(3 x^{2}+3 y^{2}=27\)
- Jibu
-
- mduara ni katikati katika\((0,0)\) na radius ya\(3\).
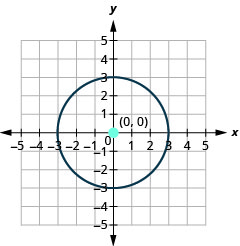
Kielelezo 11.1.25
- Pata kituo na radius, basi
- Grafu mduara:\(5 x^{2}+5 y^{2}=125\)
- Jibu
-
- mduara ni katikati katika\((0,0)\) na radius ya\(5\).
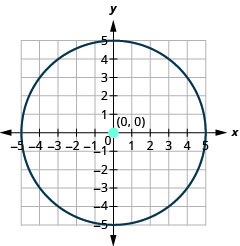
Kielelezo 11.1.26
Kama sisi kupanua equation kutoka Mfano 11.1.8,\((x+2)^{2}+(y-1)^{2}=9\), equation ya mduara inaonekana tofauti sana.
\((x+2)^{2}+(y-1)^{2}=9\)
Square binomials.
\(x^{2}+4 x+4+y^{2}-2 y+1=9\)
Panga masharti katika kushuka ili shahada, na kupata sifuri juu ya haki
\(x^{2}+y^{2}+4 x-2 y-4=0\)
Fomu hii ya equation inaitwa fomu ya jumla ya equation ya mduara.
Fomu ya jumla ya equation ya mduara ni
\(x^{2}+y^{2}+a x+b y+c=0\)
Ikiwa tunapewa equation kwa fomu ya jumla, tunaweza kuibadilisha kwa fomu ya kawaida kwa kukamilisha mraba katika wote wawili\(x\) na\(y\). Kisha tunaweza kupiga mduara kwa kutumia kituo chake na radius.
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}-4 x-6 y+4=0\)
Suluhisho:
Tunahitaji kuandika tena fomu hii ya jumla katika fomu ya kawaida ili kupata kituo na radius.
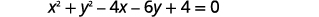
|
|
| Group\(x\) -masharti na\(y\) -masharti. Kukusanya constants upande wa kulia. |
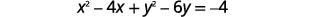
|
| Jaza mraba. |
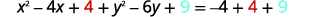
|
| Andika upya kama viwanja vya binomial. |
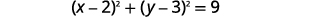
|
| Tambua kituo na radius. | Kituo:\((2,3)\) radius:\(3\) |
| Grafu mduara. |
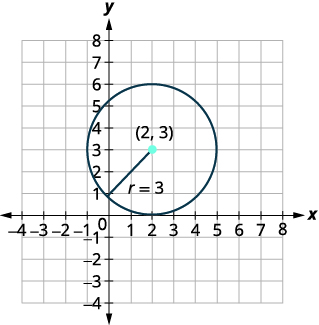
|
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}-6 x-8 y+9=0\).
- Jibu
-
- mduara ni katikati katika\((3,4)\) na radius ya\(4\).
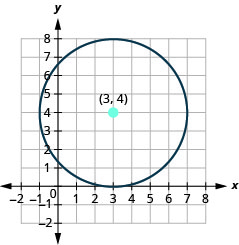
Kielelezo 11.1.32
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}+6 x-2 y+1=0\)
- Jibu
-
- mduara ni katikati katika\((-3,1)\) na radius ya\(3\).
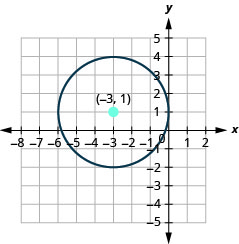
Kielelezo 11.1.33
Katika mfano unaofuata, kuna\(y\) -mrefu na\(y^{2}\) -mrefu. Lakini taarifa kwamba hakuna\(x\) -mrefu, tu\(x^{2}\) -mrefu. Tumeona hii kabla na kujua kwamba ina maana\(h\) ni\(0\). Tutahitaji kukamilisha mraba kwa\(y\) masharti, lakini si kwa\(x\) masharti.
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}+8 y=0\)
Suluhisho:
Tunahitaji kuandika tena fomu hii ya jumla katika fomu ya kawaida ili kupata kituo na radius.
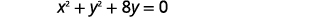 |
|
| Group\(x\) -masharti na\(y\) -masharti. | 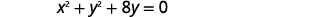 |
| Hakuna mara kwa mara kukusanya upande wa kulia. | |
| Jaza mraba kwa ajili ya\(y^{2}+8y\). | 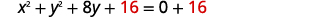 |
| Andika upya kama viwanja vya binomial. | 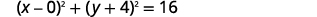 |
| Tambua kituo na radius. | Kituo:\((0,-4)\) radius:\(4\) |
| Grafu mduara. | 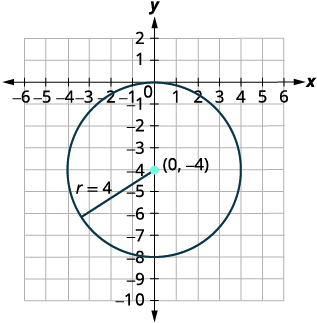 |
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}-2 x-3=0\).
- Jibu
-
- mduara ni katikati katika\((-1,0)\) na radius ya\(2\).
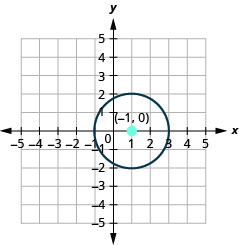
Kielelezo 11.1.39
- Pata kituo na radius, basi
- Grafu mduara:\(x^{2}+y^{2}-12 y+11=0\).
- Jibu
-
- mduara ni katikati katika\((0,6)\) na radius ya\(5\).
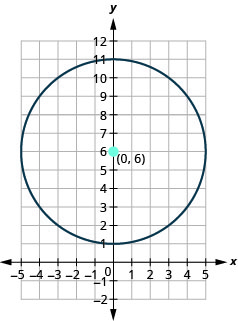
Kielelezo 11.1.40
Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi kwa kutumia umbali na midpoint formula, na graphing duru.
- Mbali-midpoint Formula na Miduara
- Kutafuta Umbali na Midpoint Kati ya Pointi mbili
- Kukamilisha Mraba Kuandika Equation katika Fomu ya kawaida ya Mzunguko
Dhana muhimu
- Umbali Mfumo: umbali\(d\) kati ya pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\) ni
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- Mfumo wa Midpoint: midpoint ya sehemu ya mstari ambao mwisho wake ni pointi mbili\(\left(x_{1}, y_{1}\right)\) na\(\left(x_{2}, y_{2}\right)\) ni
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Ili kupata midpoint ya sehemu ya mstari, tunapata wastani wa\(x\) -kuratibu na wastani wa\(y\) -kuratibu za mwisho. - Circle: Mduara ni pointi zote katika ndege ambayo ni umbali fasta kutoka hatua fasta katika ndege. Hatua iliyotolewa inaitwa kituo,\((h,k)\), na umbali uliowekwa huitwa radius,\(r\), ya mduara.
- Standard Fomu ya Equation Circle: aina ya kiwango cha equation ya mduara na kituo cha,\((h,k)\), na Radius,\(r\), ni
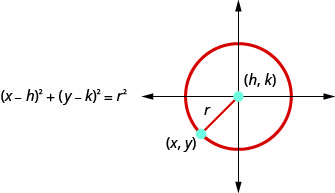
- Fomu ya jumla ya Equation ya Circle: Aina ya jumla ya equation ya mduara ni
\(x^{2}+y^{2}+a x+b y+c=0\)
faharasa
- mduara
- Mduara ni pointi zote katika ndege ambayo ni umbali fasta kutoka hatua fasta katika ndege.


