9.6: Tatua Matumizi ya Ulinganifu wa Quadratic

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

• Tatua maombi yaliyotokana na equations quadratic

Kabla ya kuanza, fanya jaribio hili la utayari.

1. Jumla ya namba mbili za mfululizo isiyo ya kawaida ni\(−100\). Kupata idadi.
   Kama amekosa tatizo hili, mapitio Mfano 2.18.
2. Kutatua:\(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\).
   Kama amekosa tatizo hili, mapitio Mfano 7.35.
3. Pata urefu wa hypotenuse ya pembetatu ya kulia na\(5\) inchi za miguu na\(12\) inchi.
   Kama amekosa tatizo hili, mapitio Mfano 2.34.

Kutatua Maombi yanayotokana na equations Quadratic

Tulitatua baadhi ya programu ambazo zinatokana na equations quadratic mapema, wakati njia pekee tulipaswa kutatua ilikuwa factoring. Sasa kwa kuwa tuna mbinu zaidi za kutatua usawa wa quadratic, tutaangalia tena programu.

Hebu kwanza tufupishe njia ambazo sasa tunapaswa kutatua equations quadratic.

Njia za Kutatua Ulinganifu wa Quadratic

1. Factoring
2. Mizizi ya mraba Mali
3. Kukamilisha Square
4. Mfumo wa Quadratic

Unapotatua kila equation, chagua njia ambayo ni rahisi zaidi kwako kufanya kazi tatizo. Kama ukumbusho, tutaiga Mkakati wetu wa kawaida wa kutatua matatizo hapa ili tuweze kufuata hatua.

Tumia Mkakati wa Kutatua Matatizo

1. Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
2. Tambua kile tunachotafuta.
3. Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
4. Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebraic.
5. Kutatua equation kutumia mbinu algebra.
6. Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
7. Jibu swali kwa sentensi kamili.

Tuna kutatuliwa maombi ya simu kwamba kushiriki mfululizo hata na isiyo ya kawaida integers, kwa modeling hali na equations linear. Kumbuka, tumeona kila integer hata ni\(2\) zaidi ya idadi iliyotangulia. Ikiwa tunaita kwanza\(n\), basi ijayo ni\(n+2\). Ijayo itakuwa\(n+2+2\) au\(n+4\). Hii pia ni kweli wakati sisi kutumia integers isiyo ya kawaida. Seti moja ya integers hata na seti moja ya integers isiyo ya kawaida huonyeshwa hapa chini.

\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)

\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)

Baadhi ya maombi ya integers isiyo ya kawaida au hata mfululizo yanatokana na equations quadratic. Nukuu hapo juu itakuwa na manufaa kama wewe jina vigezo.

Mfano\(\PageIndex{1}\)

Bidhaa ya integers mbili za mfululizo isiyo ya kawaida ni\(195\). Pata integers.

Suluhisho:

Hatua ya 1: Soma tatizo

Hatua ya 2: Tambua kile tunachotafuta.

Sisi ni kuangalia kwa integers mbili mfululizo isiyo ya kawaida.

Hatua ya 3: Jina kile tunachotafuta.

Hebu integer\(n=\) ya kwanza isiyo ya kawaida.

\(n+2=\)ijayo isiyo ya kawaida integer.

Hatua ya 4: Tafsiri katika equation. Sema tatizo katika sentensi moja.

“Bidhaa ya integers mbili mfululizo isiyo ya kawaida ni\(195\).” bidhaa ya integer ya kwanza isiyo ya kawaida na ya pili isiyo ya kawaida integer ni\(195\).

Tafsiri katika equation.

\(n(n+2)=195\)

Hatua ya 5: Tatua equation. Kusambaza.

\(n^{2}+2 n=195\)

Andika equation katika fomu ya kawaida.

\(n^{2}+2 n-195=0\)

Factor.

\((n+15)(n-13)=0\)

Tumia mali ya Bidhaa ya Zero.

\(n+15=0 \quad n-13=0\)

Kutatua kila equation.

\(n=-15, \quad n=13\)

Kuna maadili mawili ya\(n\) kwamba ni ufumbuzi. Hii itatupa jozi mbili za integers isiyo ya kawaida ya mfululizo kwa suluhisho letu.

\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)

Hatua ya 6: Angalia jibu.

Je, jozi hizi zinafanya kazi? Je, wao mfululizo integers isiyo ya kawaida?

\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)

Ni bidhaa zao\(195\)?

\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)

Hatua ya 7: Jibu swali.

Mbili integers mfululizo isiyo ya kawaida ambao bidhaa\(195\) ni\(13,15\) na\(-13,-15\).

Zoezi\(\PageIndex{1}\)

Bidhaa ya integers mbili za mfululizo isiyo ya kawaida ni\(99\). Pata integers.

Jibu

mbili mfululizo isiyo ya kawaida integers ambao bidhaa\(99\) ni\(9, 11\), na\(−9, −11\).

Zoezi\(\PageIndex{2}\)

Bidhaa ya integers mbili mfululizo hata ni\(168\). Pata integers.

Jibu

mbili mfululizo hata integers ambao bidhaa\(128\) ni\(12, 14\) na\(−12, −14\).

Tutatumia formula kwa eneo la pembetatu ili kutatua mfano unaofuata.

Ufafanuzi\(\PageIndex{1}\)

Eneo la Triangle

Kwa pembetatu na msingi\(b\),, na urefu\(h\),, eneo hilo\(A\), hutolewa na formula\(A=\frac{1}{2} b h\).

Kielelezo 9.5.1

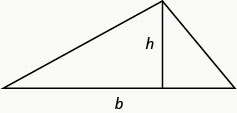
Kumbuka kwamba tunapotatua maombi ya kijiometri, ni muhimu kuteka takwimu.

Mfano\(\PageIndex{2}\)

Mbunifu ni kubuni mlango wa mgahawa. Anataka kuweka dirisha la triangular juu ya mlango. Kutokana na vikwazo vya nishati, dirisha linaweza tu kuwa na eneo la miguu ya\(120\) mraba na mbunifu anataka msingi kuwa\(4\) miguu zaidi ya mara mbili urefu. Pata msingi na urefu wa dirisha.

Suluhisho:

Jedwali 9.5.1

Hatua ya 1: Soma tatizo. Chora picha.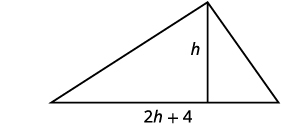
Hatua ya 2: Tambua kile tunachotafuta.	Tunatafuta msingi na urefu.
Hatua ya 3: Jina kile tunachotafuta.	Hebu\(h=\) urefu wa pembetatu. \(2h+4=\)msingi wa pembetatu.
Hatua ya 4: Tafsiri katika equation. Tunajua eneo hilo. Andika formula kwa eneo la pembetatu.	\(A=\frac{1}{2} b h\)
Hatua ya 5: Tatua equation. Mbadala katika maadili.	\(120=\frac{1}{2}(2 h+4) h\)
Kusambaza.	\(120=h^{2}+2 h\)
Hii ni equation quadratic, kuandika upya kwa fomu ya kawaida.	\(h^{2}+2 h-120=0\)
Factor.	\((h-10)(h+12)=0\)
Tumia mali ya Bidhaa ya Zero.	\(h-10=0 \quad h+12=0\)
Kurahisisha.	\(h=10, \quad \cancel{h=-12}\)
Kwa kuwa\(h\) ni urefu wa dirisha, thamani ya\(h=-12\) haina maana.
Urefu wa pembetatu\(h=10\).
Msingi wa pembetatu\(2h+4\). \(2 \cdot 10+4\) \(24\)
Hatua ya 6: Angalia jibu. Je, pembetatu yenye urefu\(10\) na msingi\(24\) ina eneo\(120\)? Ndiyo.
Hatua ya 7: Jibu swali.	Urefu wa dirisha la triangular ni\(10\) miguu na msingi ni\(24\) miguu.

Zoezi\(\PageIndex{3}\)

Pata msingi na urefu wa pembetatu ambao msingi wake ni inchi nne zaidi ya mara sita urefu wake na una eneo la inchi za\(456\) mraba.

Jibu

Urefu wa pembetatu ni\(12\) inchi na msingi ni\(76\) inchi.

Zoezi\(\PageIndex{4}\)

Ikiwa pembetatu iliyo na eneo la miguu ya\(110\) mraba ina msingi yaani futi mbili chini ya urefu mara mbili, urefu wa msingi na urefu wake ni nini?

Jibu

Urefu wa pembetatu ni\(11\) miguu na msingi ni\(20\) miguu.

Katika mifano miwili iliyotangulia, idadi katika radical katika Mfumo wa Quadratic ilikuwa mraba kamili na hivyo ufumbuzi ulikuwa namba za busara. Ikiwa tunapata nambari isiyo ya maana kama suluhisho la tatizo la maombi, tutatumia calculator kupata thamani ya takriban.

Tutatumia formula kwa eneo la mstatili ili kutatua mfano unaofuata.

Ufafanuzi\(\PageIndex{2}\)

Eneo la Mstatili

Kwa mstatili na urefu\(L\),, na upana\(W\), eneo hilo\(A\), hutolewa na formula\(A=LW\).

Kielelezo 9.5.3

Mfano\(\PageIndex{3}\)

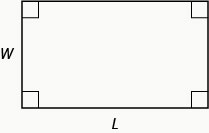
Mike anataka kuweka miguu\(150\) mraba ya Turf bandia katika yadi yake ya mbele. Hii ni eneo la juu la Turf bandia linaloruhusiwa na chama chake cha wamiliki wa nyumba. Anataka kuwa na eneo la mstatili wa turf na urefu mguu mmoja chini ya\(3\) mara upana. Pata urefu na upana. Pande zote hadi kumi ya karibu ya mguu.

Suluhisho:

Jedwali 9.5.2

Hatua ya 1: Soma tatizo. Chora picha.
Hatua ya 2: Tambua kile tunachotafuta.	Tunatafuta urefu na upana.
Hatua ya 3: Jina kile tunachotafuta.	Hebu upana\(w=\) wa mstatili. \(3w-1=\)urefu wa mstatili
Hatua ya 4: Tafsiri katika equation. Tunajua eneo hilo. Andika formula kwa eneo la mstatili.
Hatua ya 5: Tatua equation. Mbadala katika maadili.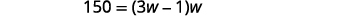
Kusambaza.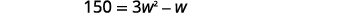
Hii ni equation quadratic; kuandika tena katika fomu ya kawaida. Tatua equation kwa kutumia Mfumo wa Quadratic.
Tambua\(a,b,c\) maadili.
Andika Mfumo wa Quadratic.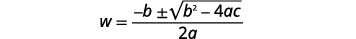
Kisha mbadala katika maadili ya\(a,b,c\).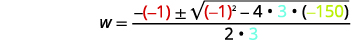
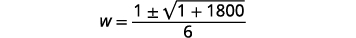
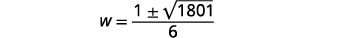
Kurahisisha.	Kielelezo 9.5.13
Andika upya ili kuonyesha ufumbuzi mbili.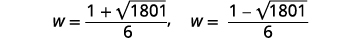
Takriban majibu kwa kutumia calculator. Sisi kuondoa ufumbuzi hasi kwa upana.
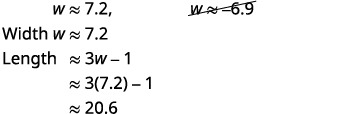Hatua ya 6: Angalia jibu. Hakikisha kwamba majibu yana maana. Kwa kuwa majibu ni takriban, eneo hilo halitatoka hasa\(150\).
Hatua ya 7: Jibu swali.	Upana wa mstatili ni takriban\(7.2\) miguu na urefu ni takriban\(20.6\) miguu.

Zoezi\(\PageIndex{5}\)

Urefu wa\(200\) mraba mguu mstatili bustani ya mboga ni miguu minne chini ya mara mbili upana. Pata urefu na upana wa bustani, hadi sehemu ya kumi ya mguu.

Jibu

Urefu wa bustani ni takriban\(18\) miguu na\(11\) miguu ya upana.

Zoezi\(\PageIndex{6}\)

Tablecloth ya mstatili ina eneo la miguu ya\(80\) mraba. Upana ni\(5\) miguu mfupi kuliko urefu.Urefu na upana wa kitambaa cha meza ni sehemu gani ya kumi ya mguu?

Jibu

Urefu wa kitambaa cha meza ni takriban\(11.8\) miguu na\(6.8\) miguu ya upana.

Theorem ya Pythagorean inatoa uhusiano kati ya miguu na hypotenuse ya pembetatu sahihi. Tutatumia Theorem ya Pythagorean kutatua mfano unaofuata.

Ufafanuzi\(\PageIndex{3}\)

Theorem ya Pythagorean

Katika pembetatu yoyote ya kulia, wapi\(a\) na\(b\) urefu wa miguu, na\(c\) ni urefu wa hypotenuse,\(a^{2}+b^{2}=c^{2}\).

Kielelezo 9.5.16

Mfano\(\PageIndex{4}\)

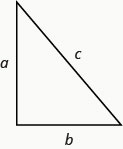
Rene ni kuanzisha likizo mwanga kuonyesha. Anataka kutengeneza 'mti' katika umbo la pembetatu mbili za kulia, kama inavyoonyeshwa hapa chini, na ana masharti mawili ya taa ya\(10\) miguu ya kutumia kwa pande. Ataunganisha taa juu ya pole na kwa vipande viwili chini. Anataka urefu wa pole kuwa sawa na umbali kutoka msingi wa pole kwa kila mti. Je, pole inapaswa kuwa mrefu gani?

Suluhisho:

Jedwali 9.5.3

Hatua ya 1: Soma tatizo. Chora picha.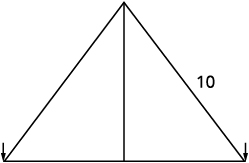
Hatua ya 2: Tambua kile tunachotafuta.	Tunatafuta urefu wa pole.
Hatua ya 3: Jina kile tunachotafuta.	Umbali kutoka kwa msingi wa pole hadi kwenye mti wowote ni sawa na urefu wa pole. Hebu\(x=\) urefu wa pole. \(x=\)umbali kutoka pole kwa hisa Kila upande ni pembetatu sahihi. Tunapata picha ya mmoja wao. 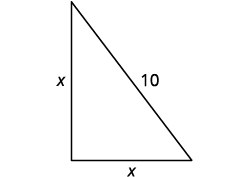Kielelezo 9.5.18
Hatua ya 4: Tafsiri katika equation. Tunaweza kutumia Theorem ya Pythagorean kutatua\(x\). Andika Theorem ya Pythagorean.	\(a^{2}+b^{2}=c^{2}\)
Hatua ya 5: Tatua equation. Mbadala.	\(x^{2}+x^{2}=10^{2}\)
Kurahisisha.	\(2 x^{2}=100\)
Gawanya na\(2\) kutenganisha kutofautiana.	\(\frac{2 x^{2}}{2}=\frac{100}{2}\)
Kurahisisha.	\(x^{2}=50\)
Tumia Mizizi ya Mizizi ya Mraba.	\(x=\pm \sqrt{50}\)
Kurahisisha radical.	\(x=\pm 5 \sqrt{2}\)
Andika upya ili kuonyesha ufumbuzi mbili.	\(x=5 \sqrt{2}, \quad \cancel{x=-5 \sqrt{2}}\)
	Ikiwa tunakaribia nambari hii hadi kumi ya karibu na calculator, tunapata\(x≈7.1\).
Hatua ya 6: Angalia jibu. Angalia mwenyewe katika Theorem ya Pythagorean.
Hatua ya 7: Jibu swali.	Pole inapaswa kuwa juu ya\(7.1\) miguu mirefu.

Zoezi\(\PageIndex{7}\)

Jua linatupa kivuli kutoka kwenye bendera ya bendera. Urefu wa pole ya bendera ni mara tatu urefu wa kivuli chake. Umbali kati ya mwisho wa kivuli na juu ya pole ya bendera ni\(20\) miguu. Find urefu wa kivuli na urefu wa pole bendera. Pande zote hadi kumi ya karibu.

Jibu

Urefu wa kivuli cha pole la bendera ni takriban\(6.3\) miguu na urefu wa pole la bendera ni\(18.9\) miguu.

Zoezi\(\PageIndex{8}\)

Umbali kati ya pembe za kinyume za shamba la mstatili ni nne zaidi ya upana wa shamba. Urefu wa shamba ni mara mbili upana wake. Pata umbali kati ya pembe za kinyume. Pande zote hadi kumi ya karibu.

Jibu

Umbali kati ya pembe za kinyume ni takriban\(7.2\) miguu.

Urefu wa projectile risasi juu kutoka chini ni inatokana na equation quadratic. Kasi ya awali\(v_{0}\), inasababisha kitu hadi mvuto husababisha kitu kuanguka chini.

Ufafanuzi\(\PageIndex{4}\)

Urefu kwa miguu,\(h\), wa kitu kilichopigwa juu ndani ya hewa na kasi ya awali,\(v_{0}\), baada ya\(t\) sekunde hutolewa na formula

\(h=-16 t^{2}+v_{0} t\)

Tunaweza kutumia formula hii ili kupata sekunde ngapi itachukua kwa ajili ya firework kufikia urefu maalum.

Mfano\(\PageIndex{5}\)

Firework ni risasi juu na\(130\) miguu ya awali kasi kwa pili. Itachukua sekunde ngapi kufikia urefu wa\(260\) miguu? Pande zote hadi kumi ya karibu ya pili.

Suluhisho:

Jedwali 9.5.4

Hatua ya 1: Soma tatizo.
Hatua ya 2: Tambua kile tunachotafuta.	Tunatafuta idadi ya sekunde, ambayo ni wakati.
Hatua ya 3: Jina kile tunachotafuta.	Hebu idadi\(t=\) ya sekunde.
Hatua ya 4: Tafsiri katika equation. Tumia formula.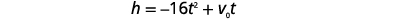
Hatua ya 5: Tatua equation. Tunajua kasi\(v_{0}\) ni\(130\) miguu kwa pili. Urefu ni\(260\) miguu. Badilisha maadili.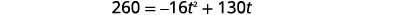
Hii ni equation quadratic, kuandika upya kwa fomu ya kawaida. Tatua equation kwa kutumia Mfumo wa Quadratic.
Kutambua maadili ya\(a, b, c\).
Andika Mfumo wa Quadratic.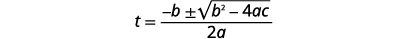
Kisha mbadala katika maadili ya\(a,b,c\).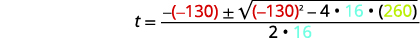
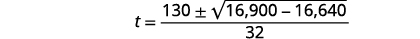
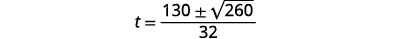
Kurahisisha.	Kielelezo 9.5.26
Andika upya ili kuonyesha ufumbuzi mbili.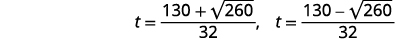
Takriban jibu na calculator.
Hatua ya 6: Angalia jibu. Cheti imesalia kwako.
Hatua ya 7: Jibu swali.	Kazi ya moto itakwenda na kisha kuanguka chini. Kama firework inakwenda juu, itafikia\(260\) miguu baada ya\(3.6\) sekunde takriban. Pia itapita urefu huo njiani chini kwa\(4.6\) sekunde.

Zoezi\(\PageIndex{9}\)

Arrow ni risasi kutoka ardhini ndani ya hewa kwa kasi ya awali ya\(108\) ft/s Matumizi formula\(h=-16 t^{2}+v_{0} t\) kuamua wakati mshale itakuwa\(180\) miguu kutoka ardhini.. Pande karibu kumi.

Jibu

Mshale utafikia\(180\) miguu njiani juu baada ya\(3\) sekunde na tena njiani chini baada ya takriban\(3.8\) sekunde.

Zoezi\(\PageIndex{10}\)

Mtu throws mpira ndani ya hewa na kasi ya\(96\) ft/s Matumizi formula\(h=-16 t^{2}+v_{0} t\) kuamua wakati urefu wa mpira itakuwa\(48\) miguu. Pande zote hadi kumi ya karibu.

Jibu

Mpira utafikia\(48\) miguu njiani juu baada ya takriban\(.6\) pili na tena njiani chini baada ya takriban\(5.4\) sekunde.

Tumetatua matatizo ya mwendo sare kwa kutumia formula\(D=rt\) katika sura zilizopita. Tulitumia meza kama ile iliyo chini ili kuandaa habari na kutuongoza kwenye equation.

Kielelezo 9.5.29

Fomu\(D=rt\) hiyo inadhani tunajua\(r\)\(t\) na tunatumia kupata\(D\). Kama tunajua\(D\) na\(r\) na haja ya kupata\(t\), tunataka kutatua equation kwa\(t\) na kupata formula\(t=\frac{D}{r}\).

Baadhi ya matatizo ya mwendo wa sare pia yanatokana na equations quadratic.

Mfano\(\PageIndex{6}\)

Profesa Smith tu akarudi kutoka mkutano iliyokuwa\(2,000\) maili mashariki ya nyumba yake. Muda wake wote katika ndege kwa safari ya pande zote ulikuwa\(9\) masaa. Ikiwa ndege ilikuwa ikiruka kwa kiwango cha\(450\) maili kwa saa, ni kasi gani ya mkondo wa ndege?

Suluhisho:

Hii ni hali ya mwendo sare. Mchoro utatusaidia kutazama hali hiyo.

Kielelezo 9.5.30

Tunajaza chati ili kuandaa habari.

Tunatafuta kasi ya mkondo wa ndege. Hebu kasi\(r=\) ya mkondo wa ndege.

Ndege inaporuka kwa upepo upepo huongeza kasi yake na hivyo kiwango ni\(450 + r\).

Ndege inapozunguka dhidi ya upepo upepo hupungua kasi yake na kiwango ni\(450 − r\).

Jedwali 9.5.5

Andika katika viwango. Andika katika umbali. Tangu\(D=r⋅t\), sisi kutatua kwa \(t\) na kupata\(t=\frac{D}{r}\). Tunagawanya umbali kwa kiwango katika kila mstari, na kuweka maneno katika safu ya wakati.
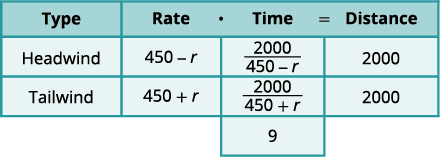Tunajua nyakati kuongeza\(9\) na hivyo sisi kuandika equation yetu.	\(\frac{2000}{450-r}+\frac{2000}{450+r}=9\)
Tunazidisha pande zote mbili na LCD.	\((450-r)(450+r)\left(\frac{2000}{450-r}+\frac{2000}{450+r}\right)=9(450-r)(450+r)\)
Kurahisisha.	\(2000(450+r)+2000(450-r)=9(450-r)(450+r)\)
sababu ya\(2,000\).	\(2000(450+r+450-r)=9\left(450^{2}-r^{2}\right)\)
Kutatua.	\(2000(900)=9\left(450^{2}-r^{2}\right)\)
Gawanya na\(9\).	\(2000(100)=450^{2}-r^{2}\)
Kurahisisha.	\(\begin{aligned}200000&=202500-r^{2} \\ -2500&=-r^{2}\\ 50&=r\end{aligned}\)\ Kasi ya mkondo wa ndege ni\(50\) mph.
Angalia: Je\(50\) mph kasi ya kuridhisha kwa mkondo wa ndege? Ndiyo. Kama ndege ni kusafiri\(450\) mph na upepo ni\(50\) mph, Tailwind \(450+50=500 \mathrm{mph} \quad \frac{2000}{500}=4\)masaa Upepo wa kichwa \(450-50=400 \mathrm{mph} \quad \frac{2000}{400}=5\)masaa Nyakati zinaongeza\(9\) masaa, hivyo hundi.

Kasi ya mkondo wa ndege ilikuwa\(50\) mph.

Zoezi\(\PageIndex{11}\)

Maryanne tu akarudi kutoka ziara na wajukuu wake nyuma mashariki. Safari hiyo ilikuwa\(2400\) maili kutoka nyumbani kwake na muda wake wote katika ndege kwa ajili ya safari ya pande zote ilikuwa\(10\) masaa. Ikiwa ndege ilikuwa ikiruka kwa kiwango cha\(500\) maili kwa saa, ni kasi gani ya mkondo wa ndege?

Jibu

Kasi ya mkondo wa ndege ilikuwa\(100\) mph.

Zoezi\(\PageIndex{12}\)

Gerry tu akarudi kutoka safari msalaba nchi. Safari hiyo ilikuwa\(3000\) maili kutoka nyumbani kwake na muda wake wote katika ndege kwa safari ya pande zote ulikuwa\(11\) masaa. Ikiwa ndege ilikuwa ikiruka kwa kiwango cha\(550\) maili kwa saa, ni kasi gani ya mkondo wa ndege?

Jibu

Kasi ya mkondo wa ndege ilikuwa\(50\) mph.

Maombi ya kazi pia yanaweza kutajwa na equations quadratic. Sisi kuweka yao juu kwa kutumia mbinu sawa sisi kutumika wakati sisi kutatuliwa yao na equations.Tutaweza kutumia mazingira sawa sasa.

Mfano\(\PageIndex{7}\)

Gazeti la uvumi la kila wiki lina habari kubwa kuhusu uchaguzi wa rais na mhariri anataka gazeti lichapishwe haraka iwezekanavyo. Amemwomba printer kuendesha vyombo vya habari vya ziada vya uchapishaji ili uchapishaji ufanyike haraka zaidi. Bonyeza #1 inachukua\(12\) masaa zaidi ya Press #2 kufanya kazi na wakati vyombo vya habari vyote viwili vinaendesha wanaweza kuchapisha kazi kwa\(8\) masaa. Inachukua muda gani kwa kila vyombo vya habari ili kuchapisha kazi peke yake?

Suluhisho:

Hili ni tatizo la kazi. Chati itatusaidia kuandaa habari.

Tunatafuta saa ngapi itachukua kila vyombo vya habari tofauti ili kukamilisha kazi.

Jedwali 9.5.6

Hebu idadi\(x=\) ya masaa kwa Press #2 kukamilisha kazi. Weka masaa kwa kazi kwa Press #1, Press #2, na wakati wao kazi pamoja.
Sehemu iliyokamilishwa na Press #1 pamoja na sehemu iliyokamilishwa na Press #2 inalingana na kiasi kilichokamilika pamoja. Tafsiri kwa equation.
Kutatua.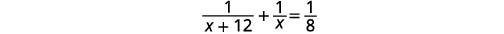
Kuzidisha kwa LCD, 8\(x(x+12)\).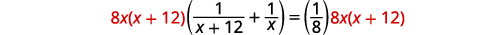
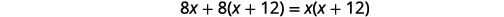
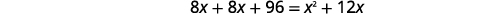
Kurahisisha.	Kielelezo 9.5.37 Kielelezo 9.5.38
Kutatua.	Kielelezo 9.5.40 Kielelezo 9.5.41
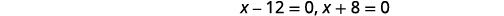
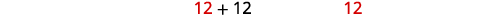
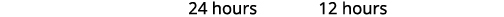
Kwa kuwa wazo la masaa hasi haina maana, tunatumia maadili\(x=12\).	Kielelezo 9.5.43
Andika jibu la sentensi yetu.	Waandishi wa habari #1 utachukua\(24\) masaa na Press #2 itachukua\(12\) masaa ya kufanya kazi peke yake.

Zoezi\(\PageIndex{13}\)

Gazeti la habari la kila wiki lina hadithi kubwa ikimtaja mtu wa Mwaka na mhariri anataka gazeti lichapishwe haraka iwezekanavyo. Amemwomba printer kuendesha vyombo vya habari vya ziada vya uchapishaji ili uchapishaji ufanyike haraka zaidi. Bonyeza #1 inachukua\(6\) masaa zaidi ya Press #2 kufanya kazi na wakati vyombo vya habari vyote viwili vinaendesha wanaweza kuchapisha kazi kwa\(4\) masaa. Inachukua muda gani kwa kila vyombo vya habari ili kuchapisha kazi peke yake?

Jibu

Waandishi wa habari #1 utachukua\(12\) masaa, na Press #2 itachukua\(6\) masaa ya kufanya kazi peke yake.

Zoezi\(\PageIndex{14}\)

Erlinda ni kuwa na chama na anataka kujaza tub yake moto. Ikiwa anatumia hose nyekundu tu inachukua\(3\) masaa zaidi kuliko kama anatumia hose ya kijani tu. Ikiwa anatumia hoses zote pamoja, tub ya moto hujaza\(2\) masaa. Inachukua muda gani kwa kila hose ili kujaza tub ya moto?

Jibu

Hose nyekundu huchukua\(6\) masaa na hose ya kijani huchukua\(3\) masaa peke yake.

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua maombi yaliyotokana na usawa wa quadratic.

• Matatizo ya Neno Kuhusisha Ulinganifu wa Quadratic
• Quadratic Equation Neno Matatizo
• Kutumia Mfumo wa Quadratic

Dhana muhimu

• Njia za Kutatua Ulinganifu wa Quadratic
  • Factoring
  • Mizizi ya mraba Mali
  • Kukamilisha Square
  • Mfumo wa Quadratic
• Jinsi ya kutumia Mkakati wa Kutatua Matatizo.
  1. Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
  2. Tambua kile tunachotafuta.
  3. Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
  4. Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebra.
  5. Kutatua equation kutumia mbinu nzuri algebra.
  6. Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
  7. Jibu swali kwa sentensi kamili.
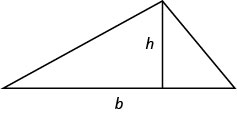
• Eneo la Triangle
  • Kwa pembetatu na msingi\(b\),, na urefu\(h\),, eneo hilo\(A\), hutolewa na formula\(A=\frac{1}{2}bh\).

Kielelezo 9.5.1

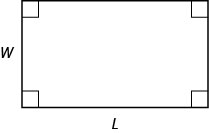
• Eneo la Mstatili
  • Kwa mstatili na urefu\(L\),, na upana\(W\), eneo hilo\(A\), hutolewa na formula\(A=LW\).

Kielelezo 9.5.3

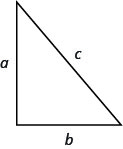
• Theorem ya Pythagorean
  • Katika pembetatu yoyote ya kulia, wapi\(a\) na\(b\) urefu wa miguu, na\(c\) ni urefu wa hypotenuse,\(a^{2}+b^{2}=c^{2}\).

Kielelezo 9.5.16

• Mwendo wa projectile
  • Urefu wa miguu,\(h\), wa kitu kilichopigwa juu ndani ya hewa na kasi ya awali,\(v_{0}\), baada ya\(t\) sekunde hutolewa na formula\(h=-16 t^{2}+v_{0} t\).