Skip to main content
Global

Sura ya 8 Mazoezi Mapitio

  1. Last updated
  2. Save as PDF
  • Page ID
    176389

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Sura ya Mapitio ya mazoezi

    Rahisisha Maneno na Mizizi

    Zoezi\(\PageIndex{1}\) Simplify Expressions with Roots

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(\sqrt{225}\)
      2. \(-\sqrt{16}\)
      1. \(-\sqrt{169}\)
      2. \(\sqrt{-8}\)
      1. \(\sqrt[3]{8}\)
      2. \(\sqrt[4]{81}\)
      3. \(\sqrt[5]{243}\)
      1. \(\sqrt[3]{-512}\)
      2. \(\sqrt[4]{-81}\)
      3. \(\sqrt[5]{-1}\)
    Jibu

    1.

    1. \(15\)
    2. \(-4\)

    3.

    1. \(2\)
    2. \(3\)
    3. \(3\)
    Zoezi\(\PageIndex{2}\) Estimate and Approximate Roots

    Katika mazoezi yafuatayo, tathmini kila mizizi kati ya namba mbili za mfululizo.

      1. \(\sqrt{68}\)
      2. \(\sqrt[3]{84}\)
    Jibu

    1.

    1. \(8<\sqrt{68}<9\)
    2. \(4<\sqrt[3]{84}<5\)
    Zoezi\(\PageIndex{3}\) Estimate and Approximate Roots

    Katika mazoezi yafuatayo, takriban kila mizizi na pande zote kwa maeneo mawili ya decimal.

      1. \(\sqrt{37}\)
      2. \(\sqrt[3]{84}\)
      3. \(\sqrt[4]{125}\)
    Jibu

    1. Tatua mwenyewe

    Zoezi\(\PageIndex{4}\) Simplify Variable Expressions with Roots

    Katika mazoezi yafuatayo, kurahisisha kutumia maadili kamili kama inavyohitajika.

      1. \(\sqrt[3]{a^{3}}\)
      2. \(\sqrt[7]{b^{7}}\)
      1. \(\sqrt{a^{14}}\)
      2. \(\sqrt{w^{24}}\)
      1. \(\sqrt[4]{m^{8}}\)
      2. \(\sqrt[5]{n^{20}}\)
      1. \(\sqrt{121 m^{20}}\)
      2. \(-\sqrt{64 a^{2}}\)
      1. \(\sqrt[3]{216 a^{6}}\)
      2. \(\sqrt[5]{32 b^{20}}\)
      1. \(\sqrt{144 x^{2} y^{2}}\)
      2. \(\sqrt{169 w^{8} y^{10}}\)
      3. \(\sqrt[3]{8 a^{51} b^{6}}\)
    Jibu

    1.

    1. \(a\)
    2. \(|b|\)

    3.

    1. \(m^{2}\)
    2. \(n^{4}\)

    5.

    1. \(6a^{2}\)
    2. \(2b^{4}\)

    Kurahisisha maneno makubwa

    Zoezi\(\PageIndex{5}\) Use the Product Property to Simplify Radical Expressions

    Katika mazoezi yafuatayo, tumia Mali ya Bidhaa ili kurahisisha maneno makubwa.

    1. \(\sqrt{125}\)
    2. \(\sqrt{675}\)
      1. \(\sqrt[3]{625}\)
      2. \(\sqrt[6]{128}\)
    Jibu

    1. \(5\sqrt{5}\)

    3.

    1. \(5 \sqrt[3]{5}\)
    2. \(2 \sqrt[6]{2}\)
    Zoezi\(\PageIndex{6}\) Use the Product Property to Simplify Radical Expressions

    Katika mazoezi yafuatayo, kurahisisha kutumia ishara za thamani kamili kama inahitajika.

      1. \(\sqrt{a^{23}}\)
      2. \(\sqrt[3]{b^{8}}\)
      3. \(\sqrt[8]{c^{13}}\)
      1. \(\sqrt{80 s^{15}}\)
      2. \(\sqrt[5]{96 a^{7}}\)
      3. \(\sqrt[6]{128 b^{7}}\)
      1. \(\sqrt{96 r^{3} s^{3}}\)
      2. \(\sqrt[3]{80 x^{7} y^{6}}\)
      3. \(\sqrt[4]{80 x^{8} y^{9}}\)
      1. \(\sqrt[5]{-32}\)
      2. \(\sqrt[8]{-1}\)
      1. \(8+\sqrt{96}\)
      2. \(\frac{2+\sqrt{40}}{2}\)
    Jibu

    2.

    1. \(4\left|s^{7}\right| \sqrt{5 s}\)
    2. \(2 a \sqrt[5]{3 a^{2}}\)
    3. \(2|b| \sqrt[6]{2 b}\)

    4.

    1. \(-2\)
    2. si kweli
    Zoezi\(\PageIndex{7}\) Use the Quotient Property to Simplify Radical Expressions

    Katika mazoezi yafuatayo, tumia Mali ya Quotient ili kurahisisha mizizi ya mraba.

      1. \(\sqrt{\frac{72}{98}}\)
      2. \(\sqrt[3]{\frac{24}{81}}\)
      3. \(\sqrt[4]{\frac{6}{96}}\)
      1. \(\sqrt{\frac{y^{4}}{y^{8}}}\)
      2. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
      3. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    3. \(\sqrt{\frac{300 m^{5}}{64}}\)
      1. \(\sqrt{\frac{28 p^{7}}{q^{2}}}\)
      2. \(\sqrt[3]{\frac{81 s^{8}}{t^{3}}}\)
      3. \(\sqrt[4]{\frac{64 p^{15}}{q^{12}}}\)
      1. \(\sqrt{\frac{27 p^{2} q}{108 p^{4} q^{3}}}\)
      2. \(\sqrt[3]{\frac{16 c^{5} d^{7}}{250 c^{2} d^{2}}}\)
      3. \(\sqrt[6]{\frac{2 m^{9} n^{7}}{128 m^{3} n}}\)
      1. \(\frac{\sqrt{80 q^{5}}}{\sqrt{5 q}}\)
      2. \(\frac{\sqrt[3]{-625}}{\sqrt[3]{5}}\)
      3. \(\frac{\sqrt[4]{80 m^{7}}}{\sqrt[4]{5 m}}\)
    Jibu

    1.

    1. \(\frac{6}{7}\)
    2. \(\frac{2}{3}\)
    3. \(\frac{1}{2}\)

    3. \(\frac{10 m^{2} \sqrt{3 m}}{8}\)

    5.

    1. \(\frac{1}{2|p q|}\)
    2. \(\frac{2 c d \sqrt[5]{2 d^{2}}}{5}\)
    3. \(\frac{|m n| \sqrt[6]{2}}{2}\)

    Kurahisisha Watazamaji wa

    Zoezi\(\PageIndex{8}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Katika mazoezi yafuatayo, andika kama kujieleza kwa kiasi kikubwa.

      1. \(r^{\frac{1}{2}}\)
      2. \(s^{\frac{1}{3}}\)
      3. \(t^{\frac{1}{4}}\)
    Jibu

    1.

    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    Zoezi\(\PageIndex{9}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Katika mazoezi yafuatayo, andika kwa ufafanuzi wa busara.

      1. \(\sqrt{21p}\)
      2. \(\sqrt[4]{8q}\)
      3. \(4\sqrt[6]{36r}\)
    Jibu

    1. Tatua mwenyewe

    Zoezi\(\PageIndex{10}\) Simplify Expressions with \(a^{\frac{1}{n}}\)

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(625^{\frac{1}{4}}\)
      2. \(243^{\frac{1}{5}}\)
      3. \(32^{\frac{1}{5}}\)
      1. \((-1,000)^{\frac{1}{3}}\)
      2. \(-1,000^{\frac{1}{3}}\)
      3. \((1,000)^{-\frac{1}{3}}\)
      1. \((-32)^{\frac{1}{5}}\)
      2. \((243)^{-\frac{1}{5}}\)
      3. \(-125^{\frac{1}{3}}\)
    Jibu

    1.

    1. \(5\)
    2. \(3\)
    3. \(2\)

    3.

    1. \(-2\)
    2. \(\frac{1}{3}\)
    3. \(-5\)
    Zoezi\(\PageIndex{11}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    Katika mazoezi yafuatayo, andika kwa ufafanuzi wa busara.

      1. \(\sqrt[4]{r^{7}}\)
      2. \((\sqrt[5]{2 p q})^{3}\)
      3. \(\sqrt[4]{\left(\frac{12 m}{7 n}\right)^{3}}\)
    Jibu

    1. Tatua mwenyewe

    Zoezi\(\PageIndex{12}\) Simplify Expressions with \(a^{\frac{m}{n}}\)

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(25^{\frac{3}{2}}\)
      2. \(9^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{2}{3}}\)
      1. \(-64^{\frac{3}{2}}\)
      2. \(-64^{-\frac{3}{2}}\)
      3. \((-64)^{\frac{3}{2}}\)
    Jibu

    1.

    1. \(125\)
    2. \(\frac{1}{27}\)
    3. \(16\)
    Zoezi\(\PageIndex{13}\) Use the Laws of Exponents to Simplify Expressions with Rational Exponents

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(6^{\frac{5}{2}} \cdot 6^{\frac{1}{2}}\)
      2. \(\left(b^{15}\right)^{\frac{3}{5}}\)
      3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
      1. \(\frac{a^{\frac{3}{4}} \cdot a^{-\frac{1}{4}}}{a^{-\frac{10}{4}}}\)
      2. \(\left(\frac{27 b^{\frac{2}{3}} c^{-\frac{5}{2}}}{b^{-\frac{7}{3}} c^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    Jibu

    1.

    1. \(6^{3}\)
    2. \(b^{9}\)
    3. \(\frac{1}{w}\)

    Ongeza, Ondoa na Kuzidisha Maneno makubwa

    Zoezi\(\PageIndex{14}\) add and Subtract Radical Expressions

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(7 \sqrt{2}-3 \sqrt{2}\)
      2. \(7 \sqrt[3]{p}+2 \sqrt[3]{p}\)
      3. \(5 \sqrt[3]{x}-3 \sqrt[3]{x}\)
      1. \(\sqrt{11 b}-5 \sqrt{11 b}+3 \sqrt{11 b}\)
      2. \(8 \sqrt[4]{11 c d}+5 \sqrt[4]{11 c d}-9 \sqrt[4]{11 c d}\)
      1. \(\sqrt{48}+\sqrt{27}\)
      2. \(\sqrt[3]{54}+\sqrt[3]{128}\)
      3. \(6 \sqrt[4]{5}-\frac{3}{2} \sqrt[4]{320}\)
      1. \(\sqrt{80 c^{7}}-\sqrt{20 c^{7}}\)
      2. \(2 \sqrt[4]{162 r^{10}}+4 \sqrt[4]{32 r^{10}}\)
    5. \(3 \sqrt{75 y^{2}}+8 y \sqrt{48}-\sqrt{300 y^{2}}\)
    Jibu

    1.

    1. \(4\sqrt{2}\)
    2. \(9\sqrt[3]{p}\)
    3. \(2\sqrt[3]{x}\)

    3.

    1. \(7\sqrt{3}\)
    2. \(7\sqrt[3]{2}\)
    3. \(3\sqrt[4]{5}\)

    5. \(37 y \sqrt{3}\)

    Zoezi\(\PageIndex{15}\) Multiply Radical Expressions

    Katika mazoezi yafuatayo, kurahisisha.

      1. \((5 \sqrt{6})(-\sqrt{12})\)
      2. \((-2 \sqrt[4]{18})(-\sqrt[4]{9})\)
      1. \(\left(3 \sqrt{2 x^{3}}\right)\left(7 \sqrt{18 x^{2}}\right)\)
      2. \(\left(-6 \sqrt[3]{20 a^{2}}\right)\left(-2 \sqrt[3]{16 a^{3}}\right)\)
    Jibu

    2.

    1. \(126 x^{2} \sqrt{2}\)
    2. \(48 a \sqrt[3]{a^{2}}\)
    Zoezi\(\PageIndex{16}\) Use Polynomial Multiplication to Multiply Radical Expressions

    Katika mazoezi yafuatayo, ongeze.

      1. \(\sqrt{11}(8+4 \sqrt{11})\)
      2. \(\sqrt[3]{3}(\sqrt[3]{9}+\sqrt[3]{18})\)
      1. \((3-2 \sqrt{7})(5-4 \sqrt{7})\)
      2. \((\sqrt[3]{x}-5)(\sqrt[3]{x}-3)\)
    3. \((2 \sqrt{7}-5 \sqrt{11})(4 \sqrt{7}+9 \sqrt{11})\)
      1. \((4+\sqrt{11})^{2}\)
      2. \((3-2 \sqrt{5})^{2}\)
    5. \((7+\sqrt{10})(7-\sqrt{10})\)
    6. \((\sqrt[3]{3 x}+2)(\sqrt[3]{3 x}-2)\)
    Jibu

    2.

    1. \(71-22 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-8 \sqrt[3]{x}+15\)

    4.

    1. \(27+8 \sqrt{11}\)
    2. \(29-12 \sqrt{5}\)

    6. \(\sqrt[3]{9 x^{2}}-4\)

    Gawanya maneno makubwa

    Zoezi\(\PageIndex{17}\) Divide Square Roots

    Katika mazoezi yafuatayo, kurahisisha.

      1. \(\frac{\sqrt{48}}{\sqrt{75}}\)
      2. \(\frac{\sqrt[3]{81}}{\sqrt[3]{24}}\)
      1. \(\frac{\sqrt{320 m n^{-5}}}{\sqrt{45 m^{-7} n^{3}}}\)
      2. \(\frac{\sqrt[3]{16 x^{4} y^{-2}}}{\sqrt[3]{-54 x^{-2} y^{4}}}\)
    Jibu

    2.

    1. \(\frac{8 m^{4}}{3 n^{4}}\)
    2. \(-\frac{x^{2}}{2 y^{2}}\)
    Zoezi\(\PageIndex{18}\) rationalize a One Term Denominator

    Katika mazoezi yafuatayo, rationalize denominator.

      1. \(\frac{8}{\sqrt{3}}\)
      2. \(\sqrt{\frac{7}{40}}\)
      3. \(\frac{8}{\sqrt{2 y}}\)
      1. \(\frac{1}{\sqrt[3]{11}}\)
      2. \(\sqrt[3]{\frac{7}{54}}\)
      3. \(\frac{3}{\sqrt[3]{3 x^{2}}}\)
      1. \(\frac{1}{\sqrt[4]{4}}\)
      2. \(\sqrt[4]{\frac{9}{32}}\)
      3. \(\frac{6}{\sqrt[4]{9 x^{3}}}\)
    Jibu

    2.

    1. \(\frac{\sqrt[3]{121}}{11}\)
    2. \(\frac{\sqrt[3]{28}}{6}\)
    3. \(\frac{\sqrt[3]{9 x}}{x}\)
    Zoezi\(\PageIndex{19}\) Rationalize a Two Term Denominator

    Katika mazoezi yafuatayo, kurahisisha.

    1. \(\frac{7}{2-\sqrt{6}}\)
    2. \(\frac{\sqrt{5}}{\sqrt{n}-\sqrt{7}}\)
    3. \(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}-\sqrt{8}}\)
    Jibu

    1. \(-\frac{7(2+\sqrt{6})}{2}\)

    3. \(\frac{(\sqrt{x}+2 \sqrt{2})^{2}}{x-8}\)

    Kutatua equations radical

    Zoezi\(\PageIndex{20}\) Solve Radical Equations

    Katika mazoezi yafuatayo, tatua.

    1. \(\sqrt{4 x-3}=7\)
    2. \(\sqrt{5 x+1}=-3\)
    3. \(\sqrt[3]{4 x-1}=3\)
    4. \(\sqrt{u-3}+3=u\)
    5. \(\sqrt[3]{4 x+5}-2=-5\)
    6. \((8 x+5)^{\frac{1}{3}}+2=-1\)
    7. \(\sqrt{y+4}-y+2=0\)
    8. \(2 \sqrt{8 r+1}-8=2\)
    Jibu

    2. hakuna ufumbuzi

    4. \(u=3, u=4\)

    6. \(x=-4\)

    8. \(r=3\)

    Zoezi\(\PageIndex{21}\) Solve Radical Equations with Two Radicals

    Katika mazoezi yafuatayo, tatua.

    1. \(\sqrt{10+2 c}=\sqrt{4 c+16}\)
    2. \(\sqrt[3]{2 x^{2}+9 x-18}=\sqrt[3]{x^{2}+3 x-2}\)
    3. \(\sqrt{r}+6=\sqrt{r+8}\)
    4. \(\sqrt{x+1}-\sqrt{x-2}=1\)
    Jibu

    2. \(x=-8, x=2\)

    4. \(x=3\)

    Zoezi\(\PageIndex{22}\) Use Radicals in Applications

    Katika mazoezi yafuatayo, tatua. Round makadirio ya mahali moja decimal.

    1. Landscaping Reed anataka kuwa na mraba bustani njama katika mashamba yake. Ana mbolea ya kutosha kufunika eneo la miguu ya\(75\) mraba. Tumia formula\(s=\sqrt{A}\) ili kupata urefu wa kila upande wa bustani yake. Pindua majibu yako kwa kumi ya karibu ya mguu.
    2. Uchunguzi wa ajali Mpelelezi wa ajali alipima alama za skid za moja ya magari yaliyohusika katika ajali. Urefu wa alama za skid ulikuwa\(175\) miguu. Tumia formula\(s=\sqrt{24d}\) ili kupata kasi ya gari kabla ya breki zilitumika. Pindua jibu lako kwa karibu kumi.
    Jibu

    2. \(64.8\)miguu

    Tumia Radicals katika Kazi

    Zoezi\(\PageIndex{23}\) Evaluate a Radical Function

    Katika mazoezi yafuatayo, tathmini kila kazi.

    1. \(g(x)=\sqrt{6 x+1}\), tafuta
      1. \(g(4)\)
      2. \(g(8)\)
    2. \(G(x)=\sqrt{5 x-1}\), tafuta
      1. \(G(5)\)
      2. \(G(2)\)
    3. \(h(x)=\sqrt[3]{x^{2}-4}\), tafuta
      1. \(h(-2)\)
      2. \(h(6)\)
    4. Kwa kazi\(g(x)=\sqrt[4]{4-4 x}\), tafuta
      1. \(g(1)\)
      2. \(g(-3)\)
    Jibu

    2.

    1. \(G(5)=2 \sqrt{6}\)
    2. \(G(2)=3\)

    4.

    1. \(g(1)=0\)
    2. \(g(-3)=2\)
    Zoezi\(\PageIndex{24}\) Find the Domain of a Radical Function

    Katika mazoezi yafuatayo, tafuta uwanja wa kazi na uandike kikoa katika maelezo ya muda.

    1. \(g(x)=\sqrt{2-3 x}\)
    2. \(F(x)=\sqrt{\frac{x+3}{x-2}}\)
    3. \(f(x)=\sqrt[3]{4 x^{2}-16}\)
    4. \(F(x)=\sqrt[4]{10-7 x}\)
    Jibu

    2. \((2, \infty)\)

    4. \(\left[\frac{7}{10}, \infty\right)\)

    Zoezi\(\PageIndex{25}\) graph Radical Functions

    Katika mazoezi yafuatayo,

    1. pata uwanja wa kazi
    2. graph kazi
    3. tumia grafu ili ueleze upeo
    1. \(g(x)=\sqrt{x+4}\)
    2. \(g(x)=2 \sqrt{x}\)
    3. \(f(x)=\sqrt[3]{x-1}\)
    4. \(f(x)=\sqrt[3]{x}+3\)
    Jibu

    2.

    1. kikoa:\([0, \infty)\)

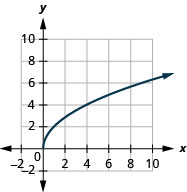
    2. Takwimu inaonyesha grafu ya kazi ya mizizi ya mraba kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka 0 hadi 8. Mhimili wa y huendesha kutoka 0 hadi 8. Kazi ina hatua ya kuanzia saa (0, 0) na hupitia pointi (1, 2) na (4, 4).
      Kielelezo 8.E.1
    3. mbalimbali:\([0, \infty)\)

    4.

    1. kikoa:\((-\infty, \infty)\)

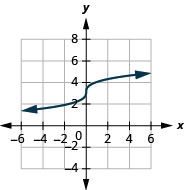
    2. Takwimu inaonyesha grafu ya kazi ya mizizi ya mchemraba kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 4 hadi 4. Mhimili wa y huendesha kutoka hasi 2 hadi 6. Kazi ina kituo cha kituo cha (0, 3) na hupitia pointi (hasi 1, 2) na (1, 4).
      Kielelezo 8.E.2
    3. mbalimbali:\((-\infty, \infty)\)

    Tumia Mfumo wa Idadi Tata

    Zoezi\(\PageIndex{26}\) evaluate the Square Root of a Negative Number

    Katika mazoezi yafuatayo, andika kila kujieleza kwa suala la\(i\) na kurahisisha iwezekanavyo.

      1. \(\sqrt{-100}\)
      2. \(\sqrt{-13}\)
      3. \(\sqrt{-45}\)
    Jibu

    Tatua mwenyewe

    Zoezi\(\PageIndex{27}\) Add or Subtract Complex Numbers

    Katika mazoezi yafuatayo, ongeza au uondoe.

    1. \(\sqrt{-50}+\sqrt{-18}\)
    2. \((8-i)+(6+3 i)\)
    3. \((6+i)-(-2-4 i)\)
    4. \((-7-\sqrt{-50})-(-32-\sqrt{-18})\)
    Jibu

    1. \(8 \sqrt{2} i\)

    3. \(8+5 i\)

    Zoezi\(\PageIndex{28}\) Multiply Complex Numbers

    Katika mazoezi yafuatayo, ongeze.

    1. \((-2-5 i)(-4+3 i)\)
    2. \(-6 i(-3-2 i)\)
    3. \(\sqrt{-4} \cdot \sqrt{-16}\)
    4. \((5-\sqrt{-12})(-3+\sqrt{-75})\)
    Jibu

    1. \(23+14 i\)

    3. \(-6\)

    Zoezi\(\PageIndex{29}\) Multiply Complex Numbers

    Katika mazoezi yafuatayo, kuzidisha kutumia Bidhaa ya Mraba ya Binomial Pattern.

    1. \((-2-3 i)^{2}\)
    Jibu

    1. \(-5-12 i\)

    Zoezi\(\PageIndex{30}\) Multiply Complex Numbers

    Katika mazoezi yafuatayo, kuzidisha kutumia Bidhaa ya Complex Conjugates Pattern.

    1. \((9-2 i)(9+2 i)\)
    Jibu

    Tatua mwenyewe

    Zoezi\(\PageIndex{31}\) divide Complex Numbers

    Katika mazoezi yafuatayo, ugawanye.

    1. \(\frac{2+i}{3-4 i}\)
    2. \(\frac{-4}{3-2 i}\)
    Jibu

    1. \(\frac{2}{25}+\frac{11}{25} i\)

    Zoezi\(\PageIndex{32}\) Simplify Powers of \(i\)

    Katika mazoezi yafuatayo, kurahisisha.

    1. \(i^{48}\)
    2. \(i^{255}\)
    Jibu

    1. \(1\)

    Mazoezi mtihani

    Zoezi\(\PageIndex{33}\)

    Katika mazoezi yafuatayo, kurahisisha kutumia maadili kamili kama inavyohitajika.

    1. \(\sqrt[3]{125 x^{9}}\)
    2. \(\sqrt{169 x^{8} y^{6}}\)
    3. \(\sqrt[3]{72 x^{8} y^{4}}\)
    4. \(\sqrt{\frac{45 x^{3} y^{4}}{180 x^{5} y^{2}}}\)
    Jibu

    1. \(5x^{3}\)

    3. \(2 x^{2} y \sqrt[3]{9 x^{2} y}\)

    Zoezi\(\PageIndex{34}\)

    Katika mazoezi yafuatayo, kurahisisha. Fikiria vigezo vyote ni chanya.

      1. \(216^{-\frac{1}{4}}\)
      2. \(-49^{\frac{3}{2}}\)
    2. \(\sqrt{-45}\)
    3. \(\frac{x^{-\frac{1}{4}} \cdot x^{\frac{5}{4}}}{x^{-\frac{3}{4}}}\)
    4. \(\left(\frac{8 x^{\frac{2}{3}} y^{-\frac{5}{2}}}{x^{-\frac{7}{3}} y^{\frac{1}{2}}}\right)^{\frac{1}{3}}\)
    5. \(\sqrt{48 x^{5}}-\sqrt{75 x^{5}}\)
    6. \(\sqrt{27 x^{2}}-4 x \sqrt{12}+\sqrt{108 x^{2}}\)
    7. \(2 \sqrt{12 x^{5}} \cdot 3 \sqrt{6 x^{3}}\)
    8. \(\sqrt[3]{4}(\sqrt[3]{16}-\sqrt[3]{6})\)
    9. \((4-3 \sqrt{3})(5+2 \sqrt{3})\)
    10. \(\frac{\sqrt[3]{128}}{\sqrt[3]{54}}\)
    11. \(\frac{\sqrt{245 x y^{-4}}}{\sqrt{45 x^{4} y^{3}}}\)
    12. \(\frac{1}{\sqrt[3]{5}}\)
    13. \(\frac{3}{2+\sqrt{3}}\)
    14. \(\sqrt{-4} \cdot \sqrt{-9}\)
    15. \(-4 i(-2-3 i)\)
    16. \(\frac{4+i}{3-2 i}\)
    17. \(i^{172}\)
    Jibu

    1.

    1. \(\frac{1}{4}\)
    2. \(-343\)

    3. \(x^{\frac{7}{4}}\)

    5. \(-x^{2} \sqrt{3 x}\)

    7. \(36 x^{4} \sqrt{2}\)

    9. \(2-7 \sqrt{3}\)

    11. \(\frac{7 x^{5}}{3 y^{7}}\)

    13. \(3(2-\sqrt{3})\)

    15. \(-12+8i\)

    17. \(-i\)

    Zoezi\(\PageIndex{35}\)

    Katika mazoezi yafuatayo, tatua.

    1. \(\sqrt{2 x+5}+8=6\)
    2. \(\sqrt{x+5}+1=x\)
    3. \(\sqrt[3]{2 x^{2}-6 x-23}=\sqrt[3]{x^{2}-3 x+5}\)
    Jibu

    2. \(x=4\)

    Zoezi\(\PageIndex{36}\)

    Katika zoezi zifuatazo,

    1. pata uwanja wa kazi
    2. graph kazi
    3. tumia grafu ili ueleze upeo
    1. \(g(x)=\sqrt{x+2}\)
    Jibu

    1.

    1. kikoa:\([-2, \infty)\)

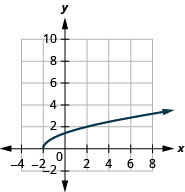
    2. Takwimu inaonyesha grafu ya kazi ya mizizi ya mraba kwenye ndege ya kuratibu x y. Mhimili wa x-wa ndege huendesha kutoka hasi 2 hadi 6. Mhimili wa y huendesha kutoka 0 hadi 8. Kazi ina hatua ya kuanzia (hasi 2, 0) na inapita kupitia pointi (hasi 1, 1) na (2, 2).
      Kielelezo 8.E.3
    3. mbalimbali:\([0, \infty)\)