Skip to main content
Global

4.5: Tatua Mifumo ya Equations na Vigezo vitatu

  1. Last updated
  2. Save as PDF
  • Page ID
    175914

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kuamua kama mara tatu iliyoamriwa ni suluhisho la mfumo wa milinganyo mitatu ya mstari na vigezo vitatu
    • Tatua mfumo wa equations linear na vigezo vitatu
    • Tatua programu kwa kutumia mifumo ya equations linear na vigezo vitatu

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Tathmini\(5x−2y+3z\) wakati\(x=−2, y=−4,\) na\(z=3.\)
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    2. Kuainisha equations kama equation masharti, utambulisho, au utata na kisha hali ya ufumbuzi. \( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
      Ikiwa umekosa tatizo hili, tathmini [kiungo].
    3. Kuainisha equations kama equation masharti, utambulisho, au utata na kisha hali ya ufumbuzi. \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. \)
      Ikiwa umekosa tatizo hili, tathmini [kiungo].

    Tambua Iwapo Triple Iliyoamriwa ni Suluhisho la Mfumo wa Ulinganisho wa Mstari wa Tatu na Vigezo

    Katika sehemu hii, tutaongeza kazi yetu ya kutatua mfumo wa equations linear. Hadi sasa tumefanya kazi na mifumo ya equations na equations mbili na vigezo viwili. Sasa tutafanya kazi na mifumo ya equations tatu na vigezo vitatu. Lakini kwanza hebu kupitia kile sisi tayari kujua kuhusu kutatua equations na mifumo kuwashirikisha hadi vigezo mbili.

    Tulijifunza mapema kwamba grafu ya equation linear\(ax+by=c\),, ni mstari. Kila hatua kwenye mstari, jozi iliyoamriwa\((x,y)\), ni suluhisho la equation. Kwa mfumo wa equations mbili na vigezo viwili, sisi grafu mistari miwili. Basi tunaweza kuona kwamba pointi zote kwamba ni ufumbuzi wa kila aina equation line. Na, kwa kutafuta nini mistari inafanana, tutapata suluhisho la mfumo.

    Wengi equations linear katika variable moja na suluhisho moja, lakini tuliona kwamba baadhi equations, aitwaye utata, hawana ufumbuzi na kwa equations nyingine, aitwaye utambulisho, namba zote ni ufumbuzi

    Tunajua wakati sisi kutatua mfumo wa equations mbili linear kuwakilishwa na grafu ya mistari miwili katika ndege moja, kuna kesi tatu iwezekanavyo, kama inavyoonekana.

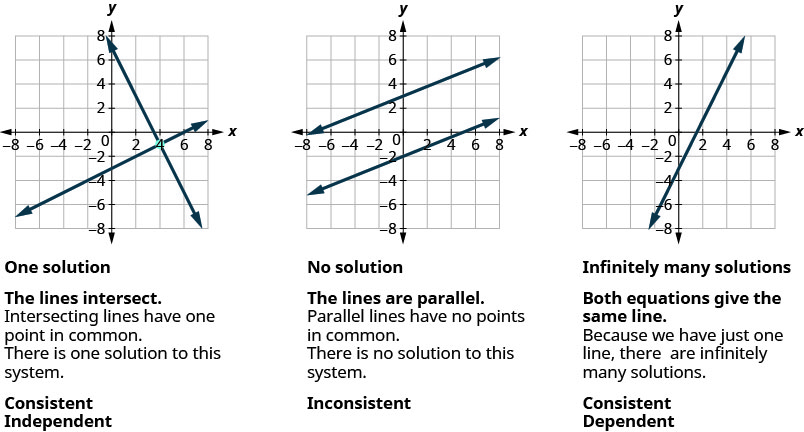
    Kielelezo kinaonyesha grafu tatu. Katika kwanza, mistari miwili inaingiliana. Mstari wa kuingiliana una hatua moja kwa pamoja. Kuna suluhisho moja kwa mfumo huu. Grafu hiyo imeandikwa Sambamba Independent. Katika grafu ya pili, mistari miwili ni sawa. Mstari wa sambamba hauna pointi sawa. Hakuna suluhisho la mfumo huu. Grafu hiyo imeandikwa haiendani. Katika grafu ya tatu, kuna mstari mmoja tu. Mlinganyo wote hutoa mstari huo. Kwa sababu tuna mstari mmoja tu, kuna ufumbuzi mkubwa sana. Ni kinachoitwa thabiti tegemezi.

    Vile vile, kwa equation linear na vigezo vitatu ax+na+cz=d, ax+na+cz=d, kila ufumbuzi wa equation ni mara tatu kuamuru, (x, y, z) (x, y, z) ambayo inafanya equation kweli.

    MSTARI WA MSTARI KATIKA VIGEZO

    equation linear na vigezo tatu, ambapo a, b, c, na d ni idadi halisi na a, b, na c si wote 0, ni ya fomu

    \[ ax+by+cz=d\nonumber \]

    Kila ufumbuzi wa equation ni kuamuru mara tatu,\((x,y,z)\) ambayo inafanya equation kweli.

    Vipengele vyote ambavyo ni ufumbuzi wa equation moja huunda ndege katika nafasi tatu-dimensional. Na, kwa kutafuta nini ndege zinafanana, tutapata suluhisho la mfumo.

    Tunapotatua mfumo wa equations tatu za mstari unaowakilishwa na grafu ya ndege tatu katika nafasi, kuna matukio matatu iwezekanavyo.

    Takwimu nane zinaonyeshwa. Ya kwanza inaonyesha ndege tatu za kuingiliana na hatua moja sawa. Ni kinachoitwa mfumo thabiti na equations Independent. Takwimu ya pili ina ndege tatu zinazofanana na hakuna pointi sawa. Ni kinachoitwa mfumo usioendana. Katika takwimu ya tatu ndege mbili ni sawa na sambamba na ndege ya tatu. Ndege hazina pointi sawa. Katika takwimu ya nne, ndege mbili ni sambamba na kila intersects ndege ya tatu. Ndege hazina pointi sawa. Katika takwimu ya tano, kila ndege inakabiliana na wengine wawili, lakini wote watatu hawashiriki pointi. Ndege hazina pointi sawa. Katika takwimu ya sita, ndege tatu zinaingiliana katika mstari mmoja. Kuna mstari mmoja tu, kwa hiyo kuna ufumbuzi mkubwa sana. Katika takwimu ya saba, ndege mbili zinajumuisha na zinaingiliana ndege ya tatu katika mstari. Kuna mstari mmoja tu, kwa hiyo kuna ufumbuzi mkubwa sana. Katika takwimu ya mwisho, ndege tatu ni sawa. Kuna ndege moja tu, kwa hiyo kuna ufumbuzi mkubwa sana........

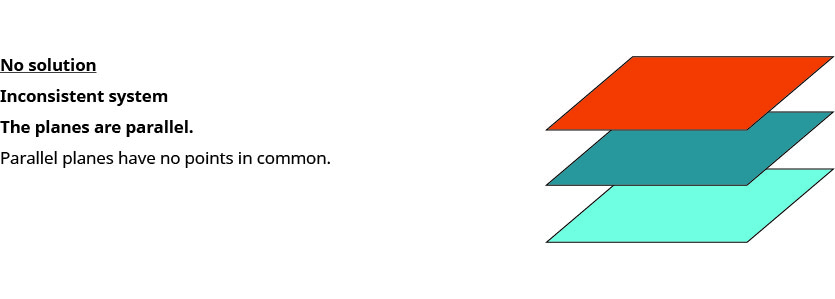
    Ili kutatua mfumo wa equations tatu za mstari, tunataka kupata maadili ya vigezo ambavyo ni ufumbuzi wa equations zote tatu. Kwa maneno mengine, tunatafuta mara tatu iliyoamriwa\((x,y,z)\) ambayo inafanya equations zote tatu kweli. Hizi huitwa ufumbuzi wa mfumo wa equations tatu za mstari na vigezo vitatu.

    UFUMBUZI WA MFUMO WA USAWA WA MSTARI NA VIGEZO VITATU

    Ufumbuzi wa mfumo wa equations ni maadili ya vigezo vinavyofanya equations zote kuwa kweli. Suluhisho linawakilishwa na mara tatu iliyoamriwa\((x,y,z)\).

    Kuamua kama mara tatu iliyoamriwa ni suluhisho la mfumo wa milinganyo mitatu, tunabadilisha maadili ya vigezo katika kila equation. Kama kuamuru mara tatu hufanya equations zote tatu kweli, ni suluhisho la mfumo.

    Mfano\(\PageIndex{1}\)

    Kuamua kama mara tatu iliyoamriwa ni suluhisho la mfumo:\( \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. \)

    ⓐ\((−2,−1,3)\) ⓑ\((−4,−3,4)\)

    Jibu

    ⓐ

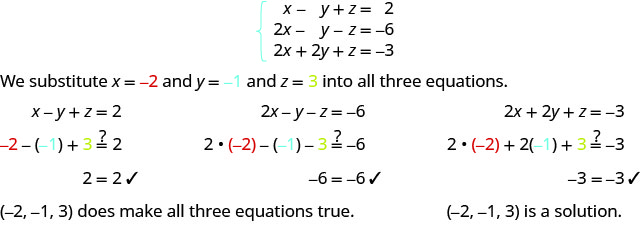
    equations ni x minus y plus z sawa 2, 2x minus y minus z sawa minus 6 na 2x pamoja 2y pamoja z sawa minus 3. Kutoa minus 2 kwa x, minus 1 kwa y na 3 kwa z katika equations zote tatu, tunaona kwamba wote watatu wanashikilia kweli. Kwa hiyo, chini ya 2, chini ya 1, 3 ni suluhisho.

    ⓑ

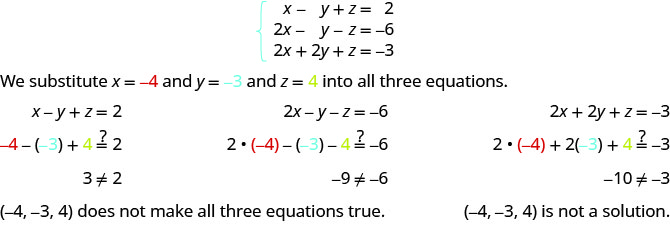
    equations ni x minus y plus z sawa 2, 2x minus y minus z sawa minus 6 na 2x pamoja 2y pamoja z sawa minus 3. Kutoa minus minus 4 kwa x, minus 3 kwa y na 4 kwa z katika equations zote tatu, tunaona kwamba wote watatu wanashikilia kweli. Kwa hiyo, minus 4, minus 3, 4 sio suluhisho.

    Mfano\(\PageIndex{2}\)

    Kuamua kama mara tatu iliyoamriwa ni suluhisho la mfumo:\( \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. \)

    ⓐ\((1,−3,2)\) ⓑ\((4,−1,−5)\)

    Jibu

    ⓐ ndiyo ⓑ hapana

    Mfano\(\PageIndex{3}\)

    Kuamua kama mara tatu iliyoamriwa ni suluhisho la mfumo:\( \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. \)

    ⓐ\((2,−2,3)\) ⓑ\((−2,2,3)\)

    Jibu

    ⓐ hapana ⓑ ndiyo

    Tatua Mfumo wa Ulinganisho wa Mstari na Vigezo vitatu

    Ili kutatua mfumo wa equations linear na vigezo tatu, sisi kimsingi kutumia mbinu hiyo sisi kutumika na mifumo ambayo ilikuwa na vigezo mbili. Tunaanza na jozi mbili za equations na katika kila jozi tunaondoa kutofautiana sawa. Hii kisha kutupa mfumo wa equations na vigezo mbili tu na kisha tunajua jinsi ya kutatua mfumo huo!

    Next, sisi kutumia maadili ya vigezo mbili sisi tu kupatikana kurudi nyuma equation awali na kupata variable tatu. Tunaandika jibu letu kama mara tatu iliyoamriwa na kisha angalia matokeo yetu.

    Mfano\(\PageIndex{4}\): How to Solve a System of Equations With Three Variables by Elimination

    Tatua mfumo kwa kuondoa:\( \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. \)

    Jibu

    equations ni x minus 2y pamoja z sawa 3, 2x pamoja y plus z sawa 4 na 3x pamoja 4y pamoja 3z sawa bala 1. Hatua ya 1 ni kuandika equations katika fomu ya kawaida. Wao ni. Ikiwa coefficients yoyote ni sehemu ndogo, wazi. Hakuna.Hatua ya 2 ni kuondoa variable sawa kutoka equations mbili. Chagua ni variable gani utaondoa. Tunaweza kuondokana na y kutoka equations 1 na 2 kwa kuzidisha equation 2 na 2. Kazi na jozi ya equations ili kuondoa variable waliochaguliwa. Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume. Ongeza milinganyo inayotokana na Hatua ya 2 ili kuondoa variable moja. equation mpya sisi kupata ni 5x pamoja 3z sawa 11.Hatua ya 3 ni kurudia hatua ya 2 kwa kutumia equations nyingine mbili na kuondoa variable sawa kama katika hatua ya 2. Tunaweza tena kuondoa y ya kutumia equations 1, 3 kwa kuzidisha equation 1 na 2. Kuongeza milinganyo mpya na matokeo itakuwa 5x pamoja 5z sawa 5.Hatua ya 4. Milinganyo miwili mpya huunda mfumo wa equations mbili na vigezo viwili. Tatua mfumo huu. Kuondoa x, tunapata sawa na minus 3. Kutoa hii katika moja ya equations mpya, tunapata x sawa na 4.Hatua ya 5 ni kutumia maadili ya vigezo viwili vinavyopatikana katika hatua ya 4 ili kupata variable ya tatu. 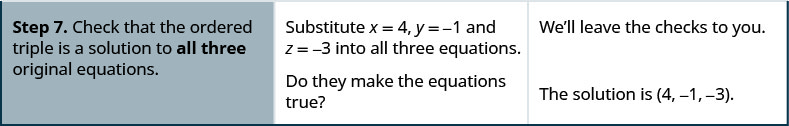Kubadilisha maadili ya x na z katika moja ya equations ya awali, tunapata y sawa na minus 1.Hatua ya 6 ni kuandika suluhisho kama amri tatu 4, minus 1, minus 3.Hatua ya 7 ni kuangalia kwamba mara tatu zilizoamriwa ni suluhisho la milinganyo yote matatu ya awali. Inafanya equations zote tatu kweli.

    Mfano\(\PageIndex{5}\)

    Tatua mfumo kwa kuondoa:\( \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.\)

    Jibu

    \((2,−1,3)\)

    Mfano\(\PageIndex{6}\)

    Tatua mfumo kwa kuondoa:\( \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. \)

    Jibu

    \((−2,3,4)\)

    Hatua hizi zimefupishwa hapa.

    TATUA MFUMO WA USAWA WA MSTARI NA VIGEZO VITATU.
    1. Andika equations katika fomu ya kawaida
      • Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
    2. Ondoa kutofautiana sawa kutoka kwa equations mbili.
      • Chagua ni variable gani utaondoa.
      • Kazi na jozi ya equations ili kuondoa variable waliochaguliwa.
      • Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
      • Ongeza equations kutokana na Hatua ya 2 ili kuondoa variable moja
    3. Kurudia Hatua ya 2 kwa kutumia equations nyingine mbili na kuondoa variable sawa kama katika Hatua ya 2.
    4. Milinganyo miwili mpya huunda mfumo wa equations mbili na vigezo viwili. Tatua mfumo huu.
    5. Tumia maadili ya vigezo viwili vilivyopatikana katika Hatua ya 4 ili kupata variable ya tatu.
    6. Andika suluhisho kama mara tatu iliyoamriwa.
    7. Angalia kwamba mara tatu zilizoamriwa ni suluhisho la milinganyo yote matatu ya awali.
    Mfano\(\PageIndex{7}\)

    Kutatua:\( \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. \)

    Jibu

    \[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]

    Tunaweza kuondoa\(z\) kutoka equations (1) na (2) kwa kuzidisha equation (2) na 2 na kisha kuongeza equations kusababisha.

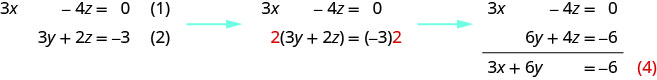
    equations ni 3 x minus 4 sawa 0, 3y pamoja na 2 z sawa na minus 3 na 2 x pamoja 3 y sawa na minus 5. Kuzidisha equation 2 na 2 na kuongeza equation 1. Tunapata 3 x pamoja na 6 y sawa na minus 6.

    Kumbuka kwamba milinganyo (3) na (4) wote wana vigezo\(x\) na\(y\). Tutatatua mfumo huu mpya kwa\(x\) na\(y\).

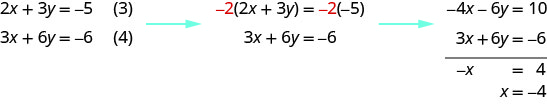
    Kuzidisha equation 3 na minus 2 na kuongeza kwamba equation 4. Tunapata x sawa na minus 4.

    Ili kutatua kwa y, sisi badala\(x=−4\) katika equation (3).

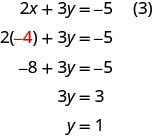
    Mbadala minus 4 katika equation 3 na kutatua kwa y. sisi kupata y sawa na 1.

    Sasa tuna\(x=−4\) na\(y=1\). Tunahitaji kutatua kwa z. Tunaweza mbadala\(x=−4\) katika equation (1) kupata z.

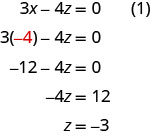
    Kutoa minus 4 katika equation 1 kwa x, tunapata z sawa na minus 3.

    Tunaandika suluhisho kama mara tatu zilizoamriwa. \((−4,1,−3)\)

    Tunaangalia kwamba suluhisho hufanya equations zote tatu kweli.

    \(\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}\)

    Mfano\(\PageIndex{8}\)

    Kutatua:\( \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. \)

    Jibu

    \((−3,4,−2)\)

    Mfano\(\PageIndex{9}\)

    Kutatua:\( \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. \)

    Jibu

    \((−2,3,−1)\)

    Wakati sisi kutatua mfumo na kuishia na hakuna vigezo na taarifa ya uongo, tunajua hakuna ufumbuzi na kwamba mfumo ni haiendani. Mfano unaofuata unaonyesha mfumo wa milinganyo ambayo haiendani.

    Mfano\(\PageIndex{10}\)

    Tatua mfumo wa equations:\( \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. \)

    Jibu

    \[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]

    Tumia equation (1) na (2) ili kuondoa z.

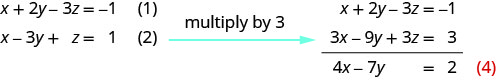
    equations ni x plus 2y minus 3z sawa minus 1, x minus 3y pamoja z sawa 1 na 2x minus y minus 2z sawa 2.

    Tumia (2) na (3) ili kuondoa\(z\) tena.

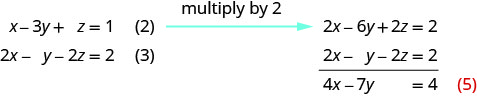
    Kuzidisha equation 2 na 3 na kuongeza kwa equation 1, sisi kupata equation 4, 4x minus 7y sawa 2. Kuzidisha equation 2 na 2 na kuongeza kwa equation 3, sisi kupata equation 5, 4x minus 7y sawa 4.

    Tumia (4) na (5) ili kuondokana na kutofautiana.

    Ulinganisho 4 na 5 wote wana vigezo 2. Kuzidisha equation 5 na minus 1 na kuongeza kwa equation 4. Tunapata 0 sawa na minus 2, ambayo ni ya uongo.

    Hakuna suluhisho.

    Sisi ni wa kushoto na taarifa ya uongo na hii inatuambia mfumo ni haiendani na haina ufumbuzi.

    Mfano\(\PageIndex{11}\)

    Tatua mfumo wa equations:\( \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. \)

    Jibu

    hakuna suluhisho

    Mfano\(\PageIndex{12}\)

    Tatua mfumo wa equations:\( \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. \)

    Jibu

    hakuna suluhisho

    Wakati sisi kutatua mfumo na kuishia na hakuna vigezo lakini taarifa ya kweli, tunajua kuna kubwa ufumbuzi wengi. Mfumo huo ni sawa na equations tegemezi. Suluhisho letu litaonyesha jinsi vigezo viwili vinategemea tatu.

    Mfano\(\PageIndex{13}\)

    Tatua mfumo wa equations:\( \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. \)

    Jibu

    \[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]

    Tumia equation (1) na (3) ili kuondoa x.

    equations ni x plus 2y bala z sawa 1, 2x pamoja 7y pamoja 4z sawa 11 na x plus 3y pamoja z sawa 4. Kuzidisha equation 1 na minus 1 na kuongeza kwa equation 3. Tunapata equation 4, y pamoja na 2z sawa 3.

    Matumizi equation (1) na (2) kuondoa x tena.

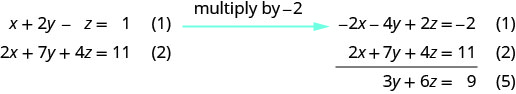
    Kuzidisha equation 1 na minus 2 na kuongeza kwa equation 2. Tunapata equation 5, 3y pamoja 6z sawa 9.

    Tumia equation (4) na (5) ili kuondoa\(y\).

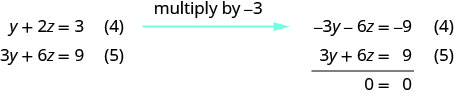
    Kuzidisha equation 4 na minus 3 na kuongeza kwa equation 5. Tunapata 0 sawa na 0. Kuna ufumbuzi usio na mwisho. Kutatua equation 4 kwa y, tunapata y sawa na minus 2z pamoja na 3. Kubadilisha hii katika equation 1, tunapata x sawa na 5z minus 5. Taarifa ya kweli 0 sawa na 0 inatuambia kwamba hii ni mfumo wa tegemezi ambao una ufumbuzi mkubwa sana. Ufumbuzi ni wa fomu x, y, z ambapo x ni 5z minus 5, y ni minus 2z pamoja 3 na z ni idadi yoyote halisi.
      Kuna ufumbuzi mkubwa sana.
    Kutatua equation (4) kwa y. Kuwakilisha suluhisho kuonyesha jinsi x na y wanategemea z.
    \( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)
    Tumia equation (1) kutatua kwa x. \( x+2y−z=1\)
    Mbadala\(y=−2z+3\). \( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \)

    Taarifa ya kweli\(0=0\) inatuambia kwamba hii ni mfumo wa tegemezi ambao una ufumbuzi mkubwa sana. Ufumbuzi ni wa fomu (x, y, z) (x, y, z) wapi\(x=5z−5;\space y=−2z+3\) na z ni idadi yoyote halisi.

    Mfano\(\PageIndex{14}\)

    Tatua mfumo kwa usawa:\( \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)

    Jibu

    infinitely wengi ufumbuzi\((x,3,z)\) ambapo\(x=z−3;\space y=3;\space z\) ni idadi yoyote halisi

    Mfano\(\PageIndex{15}\)

    Tatua mfumo kwa usawa:\( \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)

    Jibu

    infinitely wengi ufumbuzi\((x,y,z)\) ambapo\(x=5z−2;\space y=4z−3;\space z\) ni idadi yoyote halisi

    Tatua Maombi kwa kutumia Mifumo ya Ulinganisho wa mstari na Vigezo vitatu

    Maombi ambayo yanatokana na mifumo ya equations yanaweza kutatuliwa kwa kutumia mbinu sawa tulizotumia kutatua mifumo. Wengi wa maombi ni upanuzi tu kwa vigezo tatu ya aina tuna kutatuliwa mapema.

    Mfano\(\PageIndex{16}\)

    Idara ya ukumbi wa chuo cha jamii iliuza aina tatu za tiketi kwa uzalishaji wake wa hivi karibuni wa kucheza. Tiketi za watu wazima zinauzwa kwa $15, tiketi za mwanafunzi kwa $10 na tiketi za mtoto kwa $8. Idara ya ukumbi wa michezo ilifurahi kuwa na kuuzwa tiketi 250 na kuletwa $2,825 usiku mmoja. Idadi ya tiketi za wanafunzi zinazouzwa ni mara mbili idadi ya tiketi za watu wazima zinazouzwa. Ni wangapi wa kila aina ambayo idara hiyo iliuza?

    Jibu
    Tutatumia chati ili kuandaa habari. .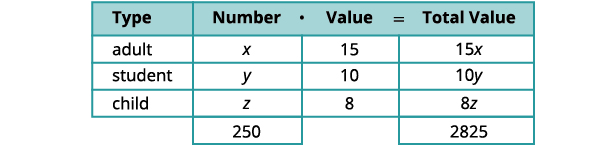
    Idadi ya wanafunzi ni mara mbili idadi ya watu wazima.  
    Andika upya equation katika fomu ya kawaida. \(\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} \)
    .
    Tumia equations (1) na (2) ili kuondoa z.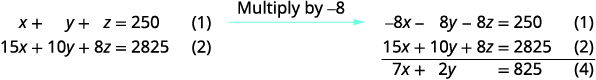  
    .
    Tumia (3) na (4) ili kuondoa\(y\).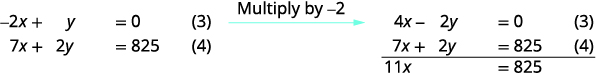  
    .
    Kutatua kwa x. \(x=75 \)tiketi ya watu wazima
    Tumia equation (3) ili kupata y. \(−2x+y=0\)
    Mbadala\(x=75\). \(\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} \)
    Tumia equation (1) ili kupata z. \(x+y+z=250\)
    Mbadala katika maadili
    \(x=75, \space y=150.\)
    \(\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} \)
    Andika suluhisho. Idara ya ukumbi iliuza tiketi 75 za watu wazima, tiketi za wanafunzi
    150, na tiketi 25 za watoto.
    Mfano\(\PageIndex{17}\)

    Idara ya sanaa ya chuo cha jamii iliuza aina tatu za tiketi kwa uwasilishaji wake wa hivi karibuni wa ngoma. Tiketi za watu wazima ziliuzwa kwa dola 20, tiketi za mwanafunzi kwa $12 na tiketi za mtoto kwa $10.Idara ya sanaa nzuri ilifurahi kuwa imeuza tiketi 350 na kuletwa $4,650 usiku mmoja. Idadi ya tiketi za watoto zinazouzwa ni sawa na idadi ya tiketi za watu wazima zinazouzwa. Ni wangapi wa kila aina ambayo idara hiyo iliuza?

    Jibu

    Idara ya sanaa nzuri iliuza tiketi 75 za watu wazima, tiketi za wanafunzi 200, na tiketi za watoto 75.

    Mfano\(\PageIndex{18}\)

    Timu ya soka ya chuo cha jamii iliuza aina tatu za tiketi kwa mchezo wake wa hivi karibuni. Tiketi za watu wazima zinauzwa kwa $10, tiketi za mwanafunzi kwa $8 na tiketi za mtoto kwa $5. Timu ya soka ilifurahi sana kuwa imeuza tiketi 600 na kuletwa katika $4,900 kwa mchezo mmoja. Idadi ya tiketi za watu wazima ni mara mbili idadi ya tiketi za watoto. Ni wangapi wa kila aina ambayo timu ya soka iliuza?

    Jibu

    Timu ya soka iliuza tiketi 200 za watu wazima, tiketi za wanafunzi 300, na tiketi 100 za watoto.

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi na kutatua mfumo wa mstari katika vigezo vitatu bila ufumbuzi au usio na mwisho.

    • Kutatua Mfumo wa Linear katika Vigezo vitatu na Hakuna au Ufumbuzi usio na mwisho
    • 3 Matumizi ya kutofautiana

    Dhana muhimu

    • Linear Equation katika Vigezo Tatu: equation linear na vigezo tatu, ambapo a, b, c, na d ni idadi halisi na a, b, na c si wote 0, ni ya fomu

      \[ax+by+cz=d\nonumber \]


      Kila ufumbuzi wa equation ni mara tatu awali,\((x,y,z)\) ambayo inafanya equation kweli.
    • Jinsi ya kutatua mfumo wa equations linear na vigezo tatu.
      1. Andika equations katika fomu ya kawaida
        Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
      2. Ondoa kutofautiana sawa kutoka kwa equations mbili.
        Chagua ni variable gani utaondoa.
        Kazi na jozi ya equations ili kuondoa variable waliochaguliwa.
        Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
        Ongeza equations kutokana na Hatua ya 2 ili kuondoa variable moja
      3. Kurudia Hatua ya 2 kwa kutumia equations nyingine mbili na kuondoa variable sawa kama katika Hatua ya 2.
      4. Milinganyo miwili mpya huunda mfumo wa equations mbili na vigezo viwili. Tatua mfumo huu.
      5. Tumia maadili ya vigezo viwili vilivyopatikana katika Hatua ya 4 ili kupata variable ya tatu.
      6. Andika suluhisho kama mara tatu iliyoamriwa.
      7. Angalia kwamba mara tatu zilizoamriwa ni suluhisho la milinganyo yote matatu ya awali.

    faharasa

    ufumbuzi wa mfumo wa equations linear na vigezo tatu
    Ufumbuzi wa mfumo wa equations ni maadili ya vigezo vinavyofanya equations zote kweli; suluhisho linawakilishwa na mara tatu iliyoamriwa (x, y, z).