11.4: Propriedades coligativas
- Page ID
- 184834
- Concentrações expressas dos componentes da solução usando fração molar e molalidade
- Descreva o efeito da concentração de soluto em várias propriedades da solução (pressão de vapor, ponto de ebulição, ponto de congelamento e pressão osmótica)
- Faça cálculos usando as equações matemáticas que descrevem esses vários efeitos coligativos
- Descreva o processo de destilação e suas aplicações práticas
- Explique o processo de osmose e descreva como ele é aplicado industrialmente e na natureza
As propriedades de uma solução são diferentes das do soluto (s) puro (s) ou do solvente. Muitas propriedades da solução dependem da identidade química do soluto. Em comparação com a água pura, uma solução de cloreto de hidrogênio é mais ácida, uma solução de amônia é mais básica, uma solução de cloreto de sódio é mais densa e uma solução de sacarose é mais viscosa. No entanto, existem algumas propriedades da solução que dependem apenas da concentração total das espécies de soluto, independentemente de suas identidades. Essas propriedades coligativas incluem redução da pressão de vapor, elevação do ponto de ebulição, depressão do ponto de congelamento e pressão osmótica. Esse pequeno conjunto de propriedades é de importância central para muitos fenômenos naturais e aplicações tecnológicas, conforme será descrito neste módulo.
Fração molar e molalidade
Várias unidades comumente usadas para expressar as concentrações dos componentes da solução foram apresentadas em um capítulo anterior deste texto, cada uma fornecendo certos benefícios para uso em diferentes aplicações. Por exemplo, a molaridade (M) é uma unidade conveniente para uso em cálculos estequiométricos, pois é definida em termos das quantidades molares das espécies de soluto:
\[M=\dfrac{\text{mol solute}}{\text{L solution}} \label{11.5.1} \]
Como os volumes da solução variam com a temperatura, as concentrações molares também variam. Quando expressa como molaridade, a concentração de uma solução com números idênticos de espécies de soluto e solvente será diferente em diferentes temperaturas, devido à contração/expansão da solução. Mais apropriadas para cálculos envolvendo muitas propriedades coligativas são as unidades de concentração baseadas em moles cujos valores não dependem da temperatura. Duas dessas unidades são a fração molar (introduzida no capítulo anterior sobre gases) e a molalidade.
A fração molar,\(\chi\), de um componente é a razão entre sua quantidade molar e o número total de moles de todos os componentes da solução:
\[\chi_\ce{A}=\dfrac{\text{mol A}}{\text{total mol of all components}} \label{11.5.2} \]
A molalidade é uma unidade de concentração definida como a razão entre o número de moles de soluto e a massa do solvente em quilogramas:
\[m=\dfrac{\text{mol solute}}{\text{kg solvent}} \label{11.5.3} \]
Como essas unidades são calculadas usando apenas massas e quantidades molares, elas não variam com a temperatura e, portanto, são mais adequadas para aplicações que exigem concentrações independentes da temperatura, incluindo várias propriedades coligativas, conforme será descrito neste módulo do capítulo.
O anticongelante na maioria dos radiadores de automóveis é uma mistura de volumes iguais de etilenoglicol e água, com pequenas quantidades de outros aditivos que evitam a corrosão. Quais são a (a) fração molar e (b) molalidade do etilenoglicol, C 2 H 4 (OH) 2, em uma solução preparada a partir\(\mathrm{2.22 \times 10^3 \;g}\) de etilenoglicol e\(\mathrm{2.00 \times 10^3\; g}\) de água (aproximadamente 2 L de glicol e 2 L de água)?
Solução
(a) A fração molar do etilenoglicol pode ser calculada derivando primeiro as quantidades molares de ambos os componentes da solução e, em seguida, substituindo essas quantidades na definição da unidade.
\(\mathrm{mol\:H_2O=2000\:g×\dfrac{1\:mol\:H_2O}{18.02\:g\:H_2O}=111\:mol\:H_2O}\)
\(\chi_\mathrm{ethylene\:glycol}=\mathrm{\dfrac{35.8\:mol\:C_2H_4(OH)_2}{(35.8+111)\:mol\: total}=0.245}\)
Observe que a fração molar é uma propriedade adimensional, sendo a proporção de propriedades com unidades idênticas (moles).
(b) Para encontrar a molalidade, precisamos conhecer os moles do soluto e a massa do solvente (em kg).
Primeiro, use a massa dada de etilenoglicol e sua massa molar para encontrar os moles do soluto:
\[\mathrm{2220\:g\:C_2H_4(OH)_2\left(\dfrac{mol\:C_2H_2(OH)_2}{62.07\:g}\right)=35.8\:mol\:C_2H_4(OH)_2} \nonumber \]
Em seguida, converta a massa da água de gramas em quilogramas:
\[\mathrm{2000\: g\:H_2O\left(\dfrac{1\:kg}{1000\:g}\right)=2\: kg\:H_2O} \nonumber \]
Finalmente, calcule a molaridade de acordo com sua definição:
\ [\ begin {align*}
\ ce {molalidade} &=\ mathrm {\ dfrac {mol\: soluto} {kg\: solvente}}\\
\ ce {molalidade} &=\ mathrm {\ dfrac {35,8\ :mol\ :C_2H_4 (OH) _2} {2\ :kg\ :H_2O}\\
\ ce {molalidade} &=17,9\ :m
\ end {align*}\ nonumber\]
Quais são a fração molar e a molalidade de uma solução que contém 0,850 g de amônia, NH 3, dissolvida em 125 g de água?
- Responda
-
7,14 × 10 −3; 0,399 m
Calcule a fração molar do soluto e do solvente em uma solução de 3,0 m de cloreto de sódio.
Leilão individual
A conversão de uma unidade de concentração para outra é realizada comparando primeiro as duas definições de unidades. Nesse caso, ambas as unidades têm o mesmo numerador (moles de soluto), mas denominadores diferentes. A concentração molal fornecida pode ser escrita como:
\[\mathrm{\dfrac{3.0\;mol\; NaCl}{1.0\; kg\; H_2O}} \nonumber \]
O numerador para a fração molar dessa solução é, portanto, 3,0 mol NaCl. O denominador pode ser calculado derivando a quantidade molar de água correspondente a 1,0 kg
\[\mathrm{1.0\:kg\:H_2O\left(\dfrac{1000\:g}{1\:kg}\right)\left(\dfrac{mol\:H_2O}{18.02\:g}\right)=55\:mol\:H_2O} \nonumber \]
e depois substituindo essas quantidades molares na definição de fração molar.
\ [\ begin {align*}
X_\ mathrm {H_2O} &=\ mathrm {\ dfrac {mol\ :H_2O} {mol\: NaCl + mol\ :H_2O}}\\
X_\ mathrm {H_2O} &=\ mathrm {\ dfrac {55\ :mol\ :H_H_B_ 2O} {3.0\ :mol\: NaCl+55\ :mol\ :H_2O}}\\
X_\ mathrm {H_2O} &=0,95\\
X_\ mathrm {NaCl} &=\ mathrm {\ dfrac {mol\: NaCl} { mol\: NaCl+mol\ :H_2O}}\\
X_\ mathrm {NaCl} &=\ mathrm {\ dfrac {3.0\ :mol\ :NaCl} {3.0\ :mol\: NaCl+55\ :mol\ :H_2O}}\\
X_\ mathrm {NaCl} &=0,052
\ end {align*}\ nonumber\]
A fração molar do iodo\(\ce{I_2}\), dissolvida em diclorometano\(\ce{CH_2Cl_2}\), é 0,115. Qual é a concentração molal, m, de iodo nessa solução?
- Responda
-
1,50 m
Redução da pressão de vapor
Conforme descrito no capítulo sobre líquidos e sólidos, a pressão de vapor de equilíbrio de um líquido é a pressão exercida por sua fase gasosa quando a vaporização e a condensação estão ocorrendo em taxas iguais:
\[ \text{liquid} \rightleftharpoons \text{gas} \label{11.5.4} \]
A dissolução de uma substância não volátil em um líquido volátil resulta em uma redução da pressão de vapor do líquido. Esse fenômeno pode ser racionalizado considerando o efeito das moléculas de soluto adicionadas nos processos de vaporização e condensação do líquido. Para vaporizar, as moléculas de solvente devem estar presentes na superfície da solução. A presença de soluto diminui a área de superfície disponível para as moléculas de solvente e, assim, reduz a taxa de vaporização do solvente. Como a taxa de condensação não é afetada pela presença de soluto, o resultado final é que o equilíbrio vaporização-condensação é alcançado com menos moléculas de solvente na fase de vapor (ou seja, a uma pressão de vapor mais baixa) (Figura\(\PageIndex{1}\)). Embora essa interpretação cinética seja útil, ela não leva em conta vários aspectos importantes da natureza coligativa da redução da pressão de vapor. Uma explicação mais rigorosa envolve a propriedade da entropia, um tópico de discussão em um capítulo de texto posterior sobre termodinâmica. Para fins de compreensão da redução da pressão de vapor de um líquido, é adequado observar que a maior entropia de uma solução em comparação com seu solvente e soluto separados serve para estabilizar efetivamente as moléculas do solvente e impedir sua vaporização. Uma pressão de vapor mais baixa resulta e um ponto de ebulição correspondentemente mais alto, conforme descrito na próxima seção deste módulo.
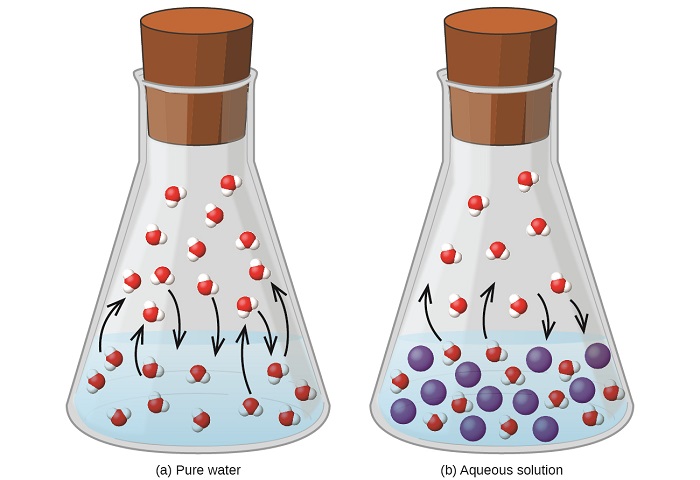
A relação entre as pressões de vapor dos componentes da solução e as concentrações desses componentes é descrita pela lei de Raoult: A pressão parcial exercida por qualquer componente de uma solução ideal é igual à pressão de vapor do componente puro multiplicada por seu mol fração na solução.
\[P_\ce{A}=X_\ce{A}P^\circ_\ce{A} \label{11.5.5} \]
onde P A é a pressão parcial exercida pelo componente A na solução,\(P^\circ_\ce{A}\) é a pressão de vapor de A puro e X A é a fração molar de A na solução. (A fração molar é uma unidade de concentração introduzida no capítulo sobre gases.)
Lembrando que a pressão total de uma mistura gasosa é igual à soma das pressões parciais de todos os seus componentes (lei de Dalton das pressões parciais), a pressão total de vapor exercida por uma solução contendo i componentes é
\[P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i \label{11.5.6} \]
Uma substância não volátil é aquela cuja pressão de vapor é insignificante (P° ≈ 0) e, portanto, a pressão de vapor acima de uma solução contendo apenas solutos não voláteis é devida apenas ao solvente:
\[P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent} \label{11.5.7} \]
Calcule a pressão de vapor de uma solução ideal contendo 92,1 g de glicerina, C 3 H 5 (OH) 3 e 184,4 g de etanol, C 2 H 5 OH, a 40 °C. A pressão de vapor do etanol puro é de 0,178 atm a 40 °C. A glicerina é essencialmente não volátil neste caso temperatura.
Solução
Como o solvente é o único componente volátil dessa solução, sua pressão de vapor pode ser calculada de acordo com a lei de Raoult como:
\(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
Primeiro, calcule as quantidades molares de cada componente da solução usando os dados de massa fornecidos.
\(\mathrm{92.1\cancel{g\:C_3H_5(OH)_3}×\dfrac{1\:mol\:C_3H_5(OH)_3}{92.094\cancel{g\:C_3H_5(OH)_3}}=1.00\:mol\:C_3H_5(OH)_3}\)
Em seguida, calcule a fração molar do solvente (etanol) e use a lei de Raoult para calcular a pressão de vapor da solução.
\(X_\mathrm{C_2H_5OH}=\mathrm{\dfrac{4.000\:mol}{(1.00\:mol+4.000\:mol)}=0.800}\)
\(P_\ce{solv}=X_\ce{solv}P^\circ_\ce{solv}=\mathrm{0.800×0.178\:atm=0.142\:atm}\)
Uma solução contém 5,00 g de ureia, CO (NH 2) 2 (um soluto não volátil) e 0,100 kg de água. Se a pressão de vapor da água pura a 25 °C for de 23,7 torr, qual é a pressão de vapor da solução?
- Responda
-
23,4 torr
Elevação do ponto de ebulição de um solvente
Conforme descrito no capítulo sobre líquidos e sólidos, o ponto de ebulição de um líquido é a temperatura na qual sua pressão de vapor é igual à pressão atmosférica ambiente. Como a pressão de vapor de uma solução é reduzida devido à presença de solutos não voláteis, é lógico que o ponto de ebulição da solução seja posteriormente aumentado. Em comparação com o solvente puro, uma solução, portanto, exigirá uma temperatura mais alta para atingir qualquer pressão de vapor, incluindo uma equivalente à da atmosfera circundante. O aumento no ponto de ebulição observado quando o soluto não volátil é dissolvido em um solvente,\(ΔT_b\), é chamado de elevação do ponto de ebulição e é diretamente proporcional à concentração molal das espécies de soluto:
\[ΔT_b=K_bm \label{11.5.8} \]
onde
- \(K_\ce{b}\)é a constante de elevação do ponto de ebulição, ou a constante ebullioscópica e
- \(m\)é a concentração molal (molalidade) de todas as espécies de soluto.
As constantes de elevação do ponto de ebulição são propriedades características que dependem da identidade do solvente. Os valores de K b para vários solventes estão listados na Tabela\(\PageIndex{1}\).
| Solvente | Ponto de ebulição (° C a 1 atm) | K b (Cm −1) | Ponto de congelamento (°C a 1 atm) | K f (Cm −1) |
|---|---|---|---|---|
| água | 100,0 | 0,512 | 0,0 | 1,86 |
| acetato de hidrogênio | 118,1 | 3,07 | 16.6 | 3.9 |
| benzeno | 80.1 | 2,53 | 5.5 | 5.12 |
| clorofórmio | 61,26 | 3,63 | −63,5 | 4,68 |
| nitrobenzeno | 210,9 | 5.24 | 5,67 | 8.1 |
A extensão em que a pressão de vapor de um solvente é reduzida e o ponto de ebulição é elevado depende do número total de partículas de soluto presentes em uma determinada quantidade de solvente, não da massa ou tamanho ou das identidades químicas das partículas. Uma solução aquosa de 1 m de sacarose (342 g/mol) e uma solução aquosa de 1 m de etilenoglicol (62 g/mol) exibirão o mesmo ponto de ebulição porque cada solução tem um mol de partículas de soluto (moléculas) por quilograma de solvente.
Qual é o ponto de ebulição de uma solução de 0,33 m de um soluto não volátil em benzeno?
Solução
Use a equação que relaciona a elevação do ponto de ebulição à molalidade do soluto para resolver esse problema em duas etapas.

- Calcule a mudança no ponto de ebulição.
\(ΔT_\ce{b}=K_\ce{b}m=2.53\:°\ce C\:m^{−1}×0.33\:m=0.83\:°\ce C\)
- Adicione a elevação do ponto de ebulição ao ponto de ebulição do solvente puro.
\(\mathrm{Boiling\: temperature=80.1\:°C+0.83\:°C=80.9\:°C}\)
Qual é o ponto de ebulição do anticongelante descrito no Exemplo\(\PageIndex{4}\)?
- Responda
-
109,2 °C
Determine o ponto de ebulição de uma solução de 92,1 g de iodo\(\ce{I2}\),, em 800,0 g de clorofórmio\(\ce{CHCl3}\),, assumindo que o iodo não é volátil e que a solução é ideal.
Solução
Podemos resolver esse problema usando quatro etapas.

- Converta de gramas em moles\(\ce{I2}\) usando a massa molar de\(\ce{I2}\) no fator de conversão unitário.
Resultado: 0,363 mol
Determine a molalidade da solução a partir do número de moles de soluto e da massa do solvente, em quilogramas.
Resultado: 0.454 m
Use a proporcionalidade direta entre a mudança no ponto de ebulição e a concentração molal para determinar o quanto o ponto de ebulição muda.
Resultado: 1.65 °C
Determine o novo ponto de ebulição a partir do ponto de ebulição do solvente puro e a mudança.
Resultado: 62.91 °C
Verifique cada resultado como uma autoavaliação.
Qual é o ponto de ebulição de uma solução de 1,0 g de glicerina\(\ce{C3H5(OH)3}\),, em 47,8 g de água? Suponha uma solução ideal.
- Responda
-
100,12 °C
Destilação de soluções
A destilação é uma técnica para separar os componentes das misturas que é amplamente aplicada tanto no laboratório quanto em ambientes industriais. É usado para refinar petróleo, isolar produtos de fermentação e purificar a água. Essa técnica de separação envolve o aquecimento controlado de uma mistura de amostra para vaporizar, condensar e coletar seletivamente um ou mais componentes de interesse. Um aparelho típico para destilações em escala de laboratório é mostrado na Figura\(\PageIndex{2}\).
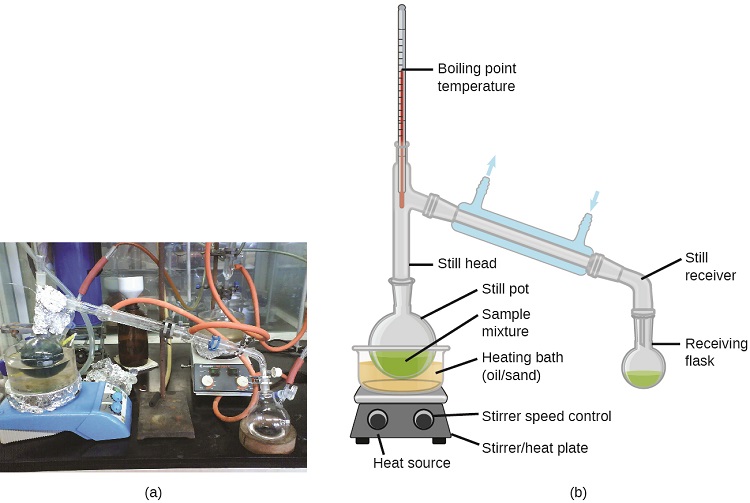
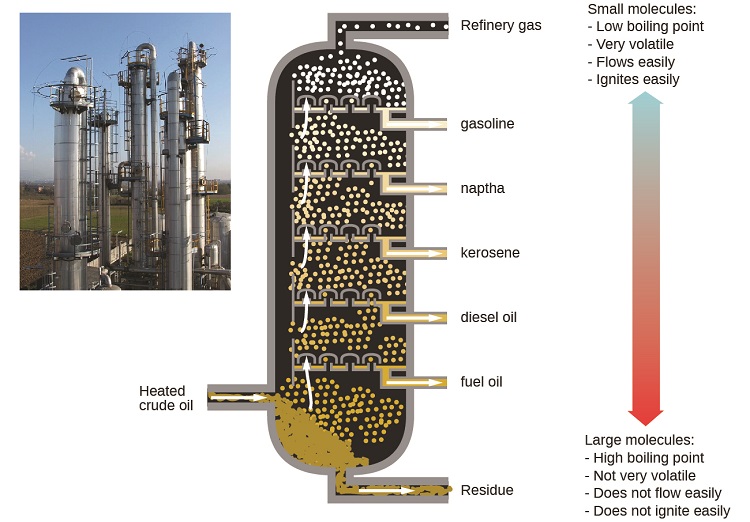
As refinarias de petróleo usam destilação fracionada em grande escala para separar os componentes do petróleo bruto. O petróleo bruto é aquecido a altas temperaturas na base de uma coluna alta de fracionamento, vaporizando muitos dos componentes que se elevam dentro da coluna. À medida que os componentes vaporizados alcançam zonas adequadamente frias durante sua subida, eles se condensam e são coletados. Os líquidos coletados são misturas mais simples de hidrocarbonetos e outros compostos de petróleo que são de composição apropriada para várias aplicações (por exemplo, combustível diesel, querosene, gasolina), conforme ilustrado na Figura\(\PageIndex{3}\).
Depressão do ponto de congelamento de um solvente
As soluções congelam em temperaturas mais baixas do que os líquidos puros. Esse fenômeno é explorado em esquemas de “degelo” que usam sal (Figura\(\PageIndex{4}\)), cloreto de cálcio ou uréia para derreter gelo em estradas e calçadas e no uso de etilenoglicol como “anticongelante” em radiadores de automóveis. A água do mar congela a uma temperatura mais baixa do que a água doce e, portanto, os oceanos Ártico e Antártico permanecem descongelados mesmo em temperaturas abaixo de 0° C (assim como os fluidos corporais de peixes e outros animais marinhos de sangue frio que vivem nesses oceanos).

A diminuição do ponto de congelamento de uma solução diluída em comparação com a do solvente puro, ΔT f, é chamada de depressão do ponto de congelamento e é diretamente proporcional à concentração molal do soluto
\[ΔT_\ce{f}=K_\ce{f}m \label{11.5.9} \]
onde
- \(m\)é a concentração molal do soluto no solvente e
- \(K_f\)é chamada de constante de depressão do ponto de congelamento (ou constante crioscópica).
Assim como as constantes de elevação do ponto de ebulição, essas são propriedades características cujos valores dependem da identidade química do solvente. Os valores de K f para vários solventes estão listados na Tabela\(\PageIndex{1}\).
Qual é o ponto de congelamento da solução de 0,33 m de um soluto não eletrolítico não volátil em benzeno descrito em Exemplo\(\PageIndex{4}\)?
Solução
Use a equação que relaciona a depressão do ponto de congelamento à molalidade do soluto para resolver esse problema em duas etapas.

- Calcule a mudança no ponto de congelamento. \[ΔT_\ce{f}=K_\ce{f}m=5.12\:°\ce C\:m^{−1}×0.33\:m=1.7\:°\ce C \nonumber \]
- Subtraia a mudança do ponto de congelamento observada do ponto de congelamento do solvente puro. \[\mathrm{Freezing\: Temperature=5.5\:°C−1.7\:°C=3.8\:°C} \nonumber \]
Qual é o ponto de congelamento de uma solução de 1,85 m de um soluto não eletrolítico não volátil em nitrobenzeno?
- Responda
-
−9,3 °C
O cloreto de sódio e seus análogos do grupo 2 cloreto de cálcio e magnésio são frequentemente usados para descongelar estradas e calçadas, devido ao fato de que uma solução de qualquer um desses sais terá um ponto de congelamento inferior a 0° C, o ponto de congelamento da água pura. Os sais metálicos do grupo 2 são frequentemente misturados com o cloreto de sódio (“sal grosso”) mais barato e mais facilmente disponível para uso em estradas, pois tendem a ser um pouco menos corrosivos que o NaCl e fornecem uma depressão maior do ponto de congelamento, pois se dissociam para produzir três partículas por unidade de fórmula, em vez de duas partículas como o cloreto de sódio.
Como esses compostos iônicos tendem a acelerar a corrosão do metal, eles não seriam uma escolha sábia para usar como anticongelante para o radiador do seu carro ou para descongelar um avião antes da decolagem. Para essas aplicações, compostos covalentes, como etileno ou propilenoglicol, são frequentemente usados. Os glicóis usados no fluido do radiador não apenas diminuem o ponto de congelamento do líquido, mas também elevam o ponto de ebulição, tornando o fluido útil tanto no inverno quanto no verão. Os glicóis aquecidos são frequentemente pulverizados na superfície dos aviões antes da decolagem em condições climáticas adversas no inverno para remover o gelo que já se formou e evitar a formação de mais gelo, o que seria particularmente perigoso se formado nas superfícies de controle da aeronave (Vídeo\(\PageIndex{1}\)).
Vídeo\(\PageIndex{1}\): A depressão do ponto de congelamento é explorada para remover o gelo das superfícies de controle da aeronave.
Diagrama de fases para uma solução aquosa de um não eletrólito
Os efeitos coligativos na pressão de vapor, ponto de ebulição e ponto de congelamento descritos na seção anterior são convenientemente resumidos comparando os diagramas de fase de um líquido puro e uma solução derivada desse líquido. Os diagramas de fase para água e uma solução aquosa são mostrados na Figura\(\PageIndex{5}\).
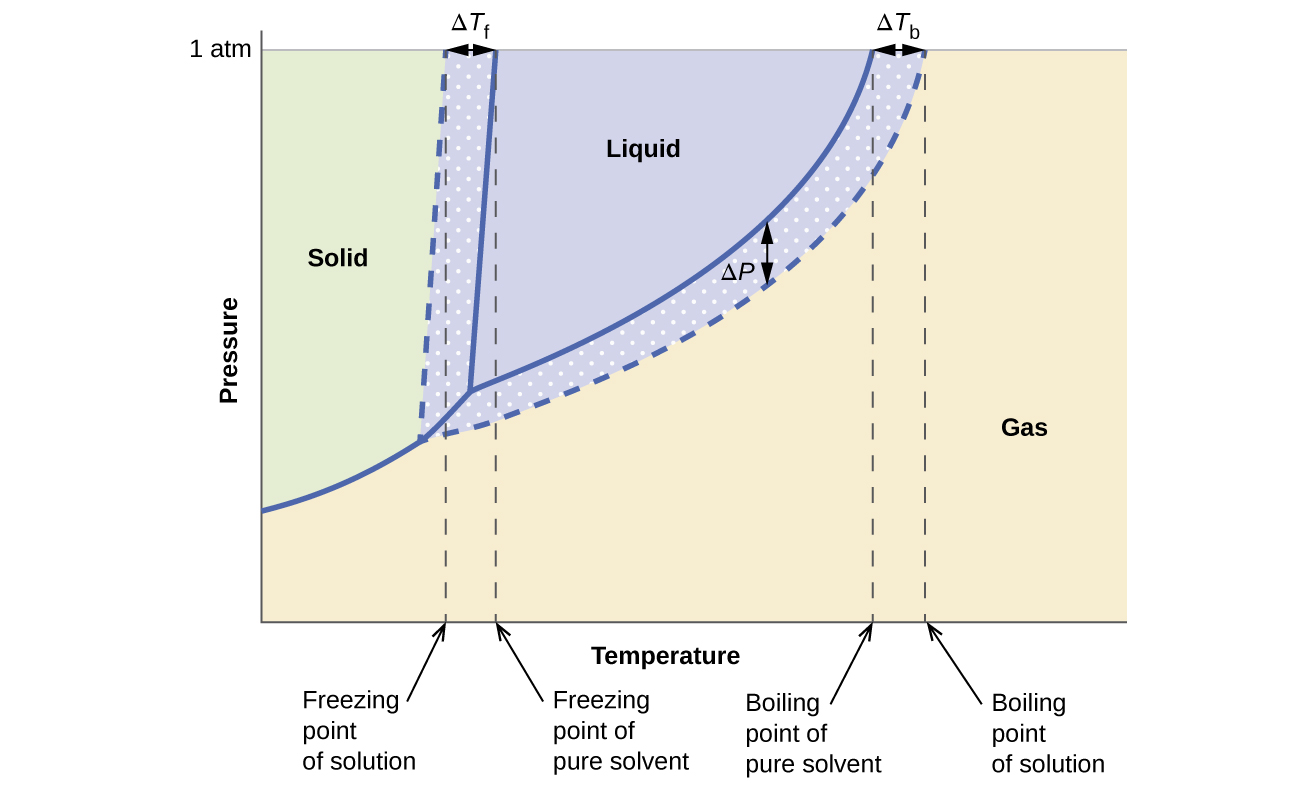
A curva de vapor líquido da solução está localizada abaixo da curva correspondente para o solvente, representando a redução da pressão de vapor, ΔP, que resulta da dissolução do soluto não volátil. Consequentemente, em qualquer pressão dada, o ponto de ebulição da solução é observado a uma temperatura mais alta do que a do solvente puro, refletindo a elevação do ponto de ebulição, ΔT b, associada à presença de soluto não volátil. A curva sólido-líquido da solução é deslocada à esquerda daquela do solvente puro, representando a depressão do ponto de congelamento, ΔTf, que acompanha a formação da solução. Finalmente, observe que as curvas de gás sólido para o solvente e sua solução são idênticas. Esse é o caso de muitas soluções que incluem solventes líquidos e solutos não voláteis. Assim como na vaporização, quando uma solução desse tipo é congelada, na verdade são apenas as moléculas de solvente que passam pela transição de líquido para sólido, formando solvente sólido puro que exclui as espécies de soluto. As fases sólida e gasosa, portanto, são compostas apenas por solvente e, portanto, as transições entre essas fases não estão sujeitas a efeitos coligativos.
Osmose e pressão osmótica de soluções
Vários materiais naturais e sintéticos exibem permeação seletiva, o que significa que somente moléculas ou íons de um determinado tamanho, forma, polaridade, carga e assim por diante, são capazes de passar (permear) o material. As membranas celulares biológicas fornecem exemplos elegantes de permeação seletiva na natureza, enquanto o tubo de diálise usado para remover resíduos metabólicos do sangue é um exemplo tecnológico mais simplista. Independentemente de como possam ser fabricados, esses materiais são geralmente chamados de membranas semipermeáveis.
Considere o aparelho ilustrado na Figura\(\PageIndex{6}\), no qual amostras de solvente puro e uma solução são separadas por uma membrana que somente moléculas de solvente podem permear. As moléculas de solvente se difundirão pela membrana em ambas as direções. Como a concentração de solvente é maior no solvente puro do que na solução, essas moléculas se difundem do lado do solvente da membrana para o lado da solução em uma taxa mais rápida do que na direção inversa. O resultado é uma transferência líquida de moléculas de solvente do solvente puro para a solução. A transferência por difusão de moléculas de solvente através de uma membrana semipermeável é um processo conhecido como osmose.
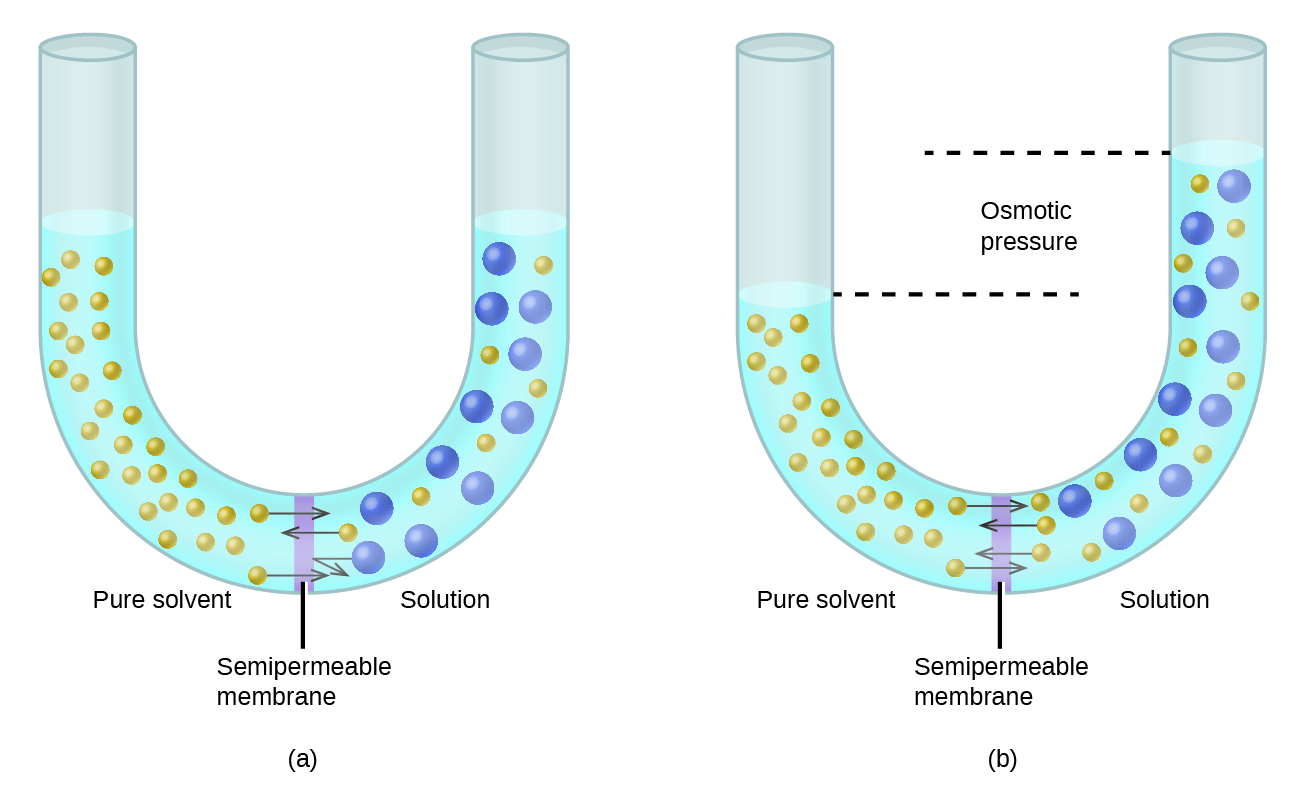
Quando a osmose é realizada em um aparelho como o mostrado na Figura\(\PageIndex{6}\), o volume da solução aumenta à medida que é diluída pelo acúmulo de solvente. Isso faz com que o nível da solução aumente, aumentando sua pressão hidrostática (devido ao peso da coluna de solução no tubo) e resultando em uma transferência mais rápida das moléculas de solvente de volta ao lado do solvente puro. Quando a pressão atinge um valor que produz uma taxa de transferência reversa de solvente igual à taxa de osmose, a transferência em massa do solvente cessa. Essa pressão é chamada de pressão osmótica (e\(\Pi\)) da solução. A pressão osmótica de uma solução diluída está relacionada à molaridade do soluto, M, e à temperatura absoluta, T, de acordo com a equação
\[Π=MRT \label{11.5.10} \]
onde\(R\) está a constante universal do gás.
Qual é a pressão osmótica (atm) de uma solução de 0,30 M de glicose em água que é usada para infusão intravenosa à temperatura corporal, 37 °C?
Solução
Podemos encontrar a pressão osmótica\(Π\), usando a Equação\ ref {11.5.10}, onde T está na escala Kelvin (310 K) e o valor de R é expresso em unidades apropriadas (0,08206 L atm/mol K).
\ [\ begin {align*}
π &=MRT\\
&=\ mathrm {0,03\ :mol/L × 0,08206\: L\: atm/mol\: K × 310\: K}\\
&=\ mathrm {7,6\ :atm}
\ end {align*}\ nonumber\]
Qual é a pressão osmótica (atm) de uma solução com volume de 0,750 L que contém 5,0 g de metanol, CH 3 OH, em água a 37 °C?
- Responda
-
5,3 atm
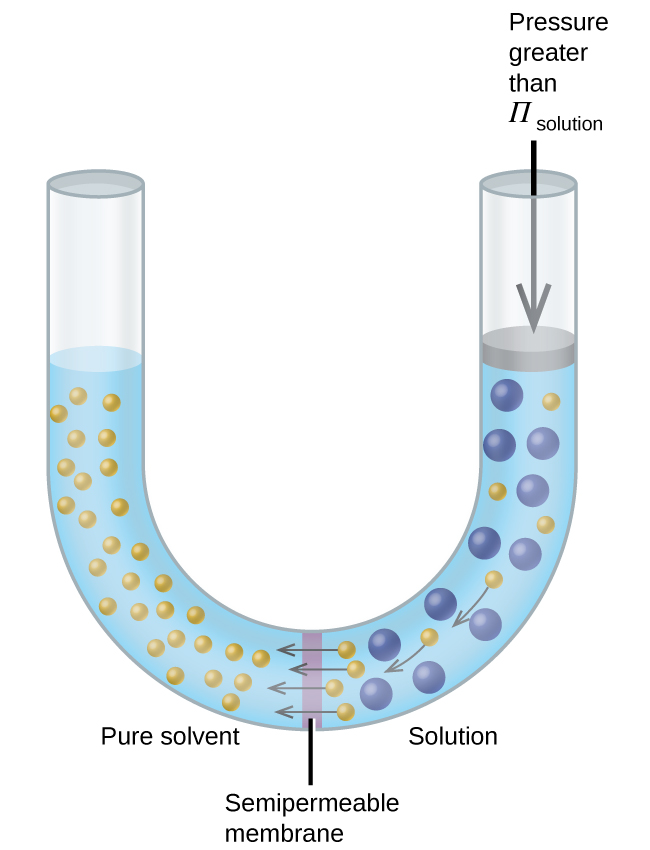
Se uma solução for colocada em um aparelho como o mostrado na Figura\(\PageIndex{7}\), aplicar pressão maior que a pressão osmótica da solução reverte a osmose e empurra as moléculas de solvente da solução para o solvente puro. Essa técnica de osmose reversa é usada para dessalinização em grande escala da água do mar e em escalas menores para produzir água de torneira de alta pureza para beber.
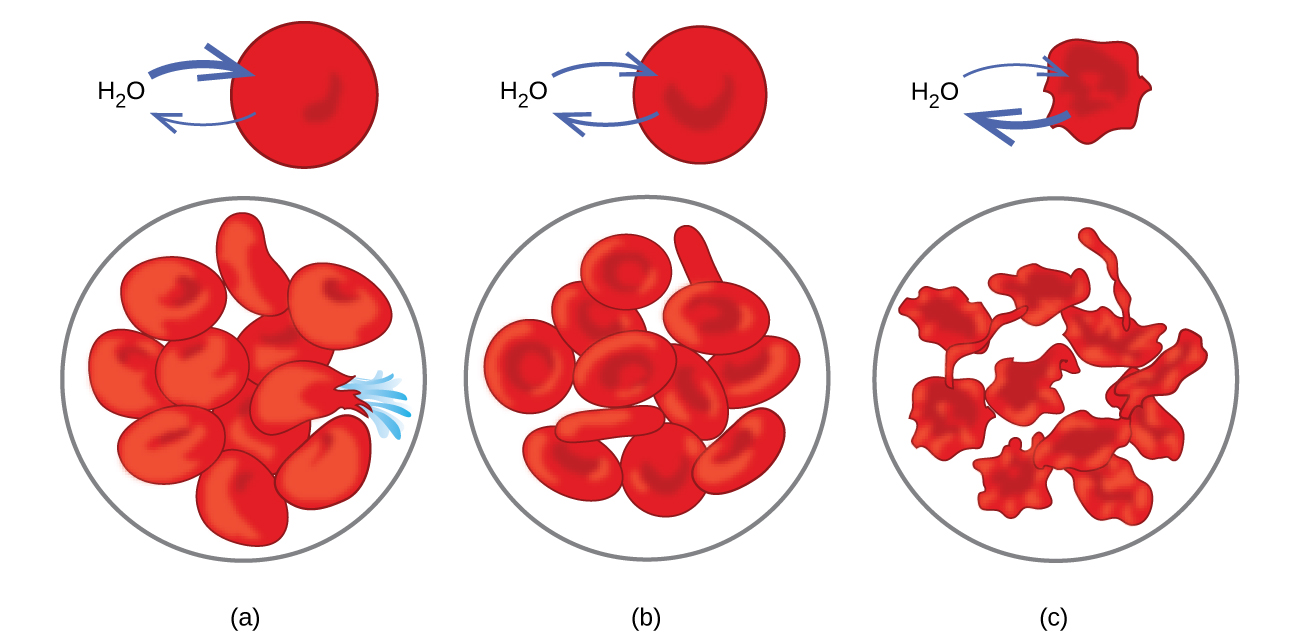
Exemplos de osmose são evidentes em muitos sistemas biológicos porque as células são cercadas por membranas semipermeáveis. Cenouras e aipo que ficaram moles porque perderam água podem ficar crocantes novamente colocando-os na água. A água entra nas células da cenoura ou do aipo por osmose. Um pepino colocado em uma solução salina concentrada perde água por osmose e absorve um pouco de sal para se tornar um picles. A osmose também pode afetar as células animais. As concentrações de soluto são particularmente importantes quando as soluções são injetadas no corpo. Os solutos nos fluidos celulares corporais e no soro sanguíneo dão a essas soluções uma pressão osmótica de aproximadamente 7,7 atm. As soluções injetadas no corpo devem ter a mesma pressão osmótica do soro sanguíneo; ou seja, devem ser isotônicas com o soro sanguíneo. Se uma solução menos concentrada, uma solução hipotônica, for injetada em quantidade suficiente para diluir o soro sanguíneo, a água do soro diluído passa para as células sanguíneas por osmose, fazendo com que as células se expandam e se rompam. Esse processo é chamado de hemólise. Quando uma solução mais concentrada, uma solução hipertônica, é injetada, as células perdem água para a solução mais concentrada, murcham e possivelmente morrem em um processo chamado crenação (Figura 11.5.8).
Determinação de massas molares
A pressão osmótica e as mudanças no ponto de congelamento, ponto de ebulição e pressão de vapor são diretamente proporcionais à concentração do soluto presente. Consequentemente, podemos usar a medição de uma dessas propriedades para determinar a massa molar do soluto a partir das medições.
Verificou-se que uma solução de 4,00 g de um não eletrólito dissolvido em 55,0 g de benzeno congela a 2,32 °C. Qual é a massa molar desse composto?
Solução
Podemos resolver esse problema usando as etapas a seguir.
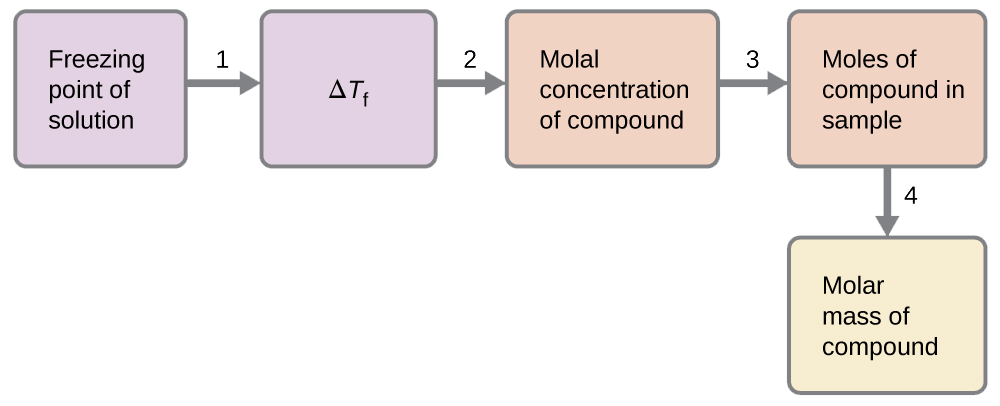
- Determine a mudança no ponto de congelamento a partir do ponto de congelamento observado e do ponto de congelamento do benzeno puro (Tabela 11.5.1).
- Determine a concentração molal de K f, a constante de depressão do ponto de congelamento para benzeno (Tabela 11.5.1) e ΔT f.
\(ΔT_\ce{f}=K_\ce{f}m\)
\(m=\dfrac{ΔT_\ce{f}}{K_\ce{f}}=\dfrac{3.2\:°\ce C}{5.12\:°\ce C m^{−1}}=0.63\:m\)
- Determine o número de moles de composto na solução a partir da concentração molal e da massa de solvente usada para fazer a solução.
\(\mathrm{Moles\: of\: solute=\dfrac{0.62\:mol\: solute}{1.00\cancel{kg\: solvent}}×0.0550\cancel{kg\: solvent}=0.035\:mol}\)
- Determine a massa molar a partir da massa do soluto e o número de moles nessa massa.
\(\mathrm{Molar\: mass=\dfrac{4.00\:g}{0.034\:mol}=1.2×10^2\:g/mol}\)
Uma solução de 35,7 g de um não eletrólito em 220,0 g de clorofórmio tem um ponto de ebulição de 64,5 °C. Qual é a massa molar desse composto?
- Responda
-
1,8 × 10 2 g/mol
Uma amostra de 0,500 L de uma solução aquosa contendo 10,0 g de hemoglobina tem uma pressão osmótica de 5,9 torr a 22 °C. Qual é a massa molar da hemoglobina?
Solução
Aqui está um conjunto de etapas que podem ser usadas para resolver o problema:

- \[\Pi=\mathrm{\dfrac{5.9\:torr×1\:atm}{760\:torr}=7.8×10^{−3}\:atm} \nonumber \]
\[\Pi=MRT \nonumber \]
\(M=\dfrac{Π}{RT}=\mathrm{\dfrac{7.8×10^{−3}\:atm}{(0.08206\:L\: atm/mol\: K)(295\:K)}=3.2×10^{−4}\:M}\)
- \(\mathrm{moles\: of\: hemoglobin=\dfrac{3.2×10^{−4}\:mol}{1\cancel{L\: solution}}×0.500\cancel{L\: solution}=1.6×10^{−4}\:mol}\)
- Determine a massa molar a partir da massa de hemoglobina e o número de moles nessa massa.
\(\mathrm{molar\: mass=\dfrac{10.0\:g}{1.6×10^{−4}\:mol}=6.2×10^4\:g/mol}\)
Qual é a massa molar de uma proteína se uma solução de 0,02 g da proteína em 25,0 mL de solução tiver uma pressão osmótica de 0,56 torr a 25 °C?
- Responda
-
2,7 × 10 4 g/mol
Propriedades coligativas dos eletrólitos
Conforme observado anteriormente neste módulo, as propriedades coligativas de uma solução dependem apenas do número, não do tipo, das espécies de soluto dissolvidas. Por exemplo, 1 mol de qualquer não eletrólito dissolvido em 1 kg de solvente produz a mesma redução do ponto de congelamento que 1 mol de qualquer outro não eletrólito. No entanto, 1 mol de cloreto de sódio (um eletrólito) forma 2 moles de íons quando dissolvido em solução. Cada íon individual produz o mesmo efeito no ponto de congelamento que uma única molécula produz.
A concentração de íons na água do mar é aproximadamente a mesma de uma solução contendo 4,2 g de NaCl dissolvido em 125 g de água. Suponha que cada um dos íons na solução de NaCl tenha o mesmo efeito no ponto de congelamento da água que uma molécula não eletrolítica e determine a temperatura de congelamento da solução (que é aproximadamente igual à temperatura de congelamento da água do mar).
Solução
Podemos resolver esse problema usando a seguinte série de etapas.
- Converta de gramas em moles de NaCl usando a massa molar de NaCl no fator de conversão unitário. Resultado: 0,072 mol NaCl
- Determine o número de moles de íons presentes na solução usando o número de moles de íons em 1 mol de NaCl como fator de conversão (íons 2 mol/1 mol NaCl). Resultado: íons de 0,14 mol
- Determine a molalidade dos íons na solução a partir do número de moles de íons e da massa do solvente, em quilogramas. Resultado: 1,1 m
- Use a proporcionalidade direta entre a mudança no ponto de congelamento e a concentração molal para determinar o quanto o ponto de congelamento muda. Resultado: 2.0 °C
- Determine o novo ponto de congelamento a partir do ponto de congelamento do solvente puro e a mudança. Resultado: −2,0 °C
Verifique cada resultado como uma autoavaliação.
Suponha que cada um dos íons no cloreto de cálcio, CaCl 2, tenha o mesmo efeito no ponto de congelamento da água que uma molécula não eletrolítica. Calcule o ponto de congelamento de uma solução de 0,724 g de CaCl 2 em 175 g de água.
- Responda
-
−0,208° C
Supondo a dissociação completa, uma solução aquosa de NaCl de 1,0 m contém 2,0 mol de íons (1,0 mol Na + e 1,0 mol Cl −) por cada quilograma de água, e espera-se que sua depressão no ponto de congelamento seja
\[ΔT_\ce{f}=\mathrm{2.0\:mol\: ions/kg\: water×1.86\:°C\: kg\: water/mol\: ion=3.7\:°C.} \label{11.5.11} \]
Quando esta solução é realmente preparada e sua depressão do ponto de congelamento é medida, no entanto, um valor de 3,4° C é obtido. Discrepâncias semelhantes são observadas para outros compostos iônicos, e as diferenças entre os valores medidos e esperados das propriedades coligativas normalmente se tornam mais significativas à medida que as concentrações de soluto aumentam. Essas observações sugerem que os íons de cloreto de sódio (e outros eletrólitos fortes) não estão completamente dissociados em solução.
Para explicar isso e evitar os erros que acompanham a suposição de dissociação total, um parâmetro medido experimentalmente, nomeado em homenagem ao químico alemão Jacobus Henricus van't Hoff, ganhador do Prêmio Nobel, é usado. O fator de van 't Hoff (i) é definido como a razão entre partículas de soluto em solução e o número de unidades de fórmula dissolvidas:
\[i=\dfrac{\textrm{moles of particles in solution}}{\textrm{moles of formula units dissolved}} \label{11.5.12} \]
Os valores dos fatores de van't Hoff medidos para vários solutos, juntamente com os valores previstos assumindo dissociação completa, são mostrados na Tabela\(\PageIndex{2}\).
| Eletrólito | Partículas em solução | i (Previsto) | i (medido) |
|---|---|---|---|
| HCl | H +, Cl - | 2 | 1.9 |
| NaCl | Na +, Cl - | 2 | 1.9 |
| MgSO 4 | Mg 2 +,\(\ce{SO4^2-}\) | 2 | 1.3 |
| MgCl 2 | Mg 2 +, 2Cl − | 3 | 2.7 |
| FeCl 3 | Fe 3 +, 3Cl − | 4 | 3.4 |
| glicose (um não eletrólito) | C 12 H 22 OU 11 | 1 | 1,0 |
Em 1923, os químicos Peter Debye e Erich Hückel propuseram uma teoria para explicar a aparente ionização incompleta de eletrólitos fortes. Eles sugeriram que, embora a atração interiônica em uma solução aquosa seja muito reduzida pela solvatação dos íons e pela ação isolante do solvente polar, ela não é completamente anulada. As atrações residuais evitam que os íons se comportem como partículas totalmente independentes (Figura\(\PageIndex{9}\)). Em alguns casos, um íon positivo e negativo podem realmente se tocar, dando uma unidade solvatada chamada par de íons. Assim, a atividade, ou a concentração efetiva, de qualquer tipo específico de íon é menor do que a indicada pela concentração real. Os íons ficam cada vez mais separados quanto mais diluída a solução, e as atrações interiônicas residuais se tornam cada vez menores. Assim, em soluções extremamente diluídas, as concentrações efetivas dos íons (suas atividades) são essencialmente iguais às concentrações reais. Observe que os fatores de van 't Hoff para os eletrólitos na Tabela\(\PageIndex{2}\) são para soluções de 0,05 m, em que concentração o valor de i para NaCl é 1,9, em oposição a um valor ideal de 2.
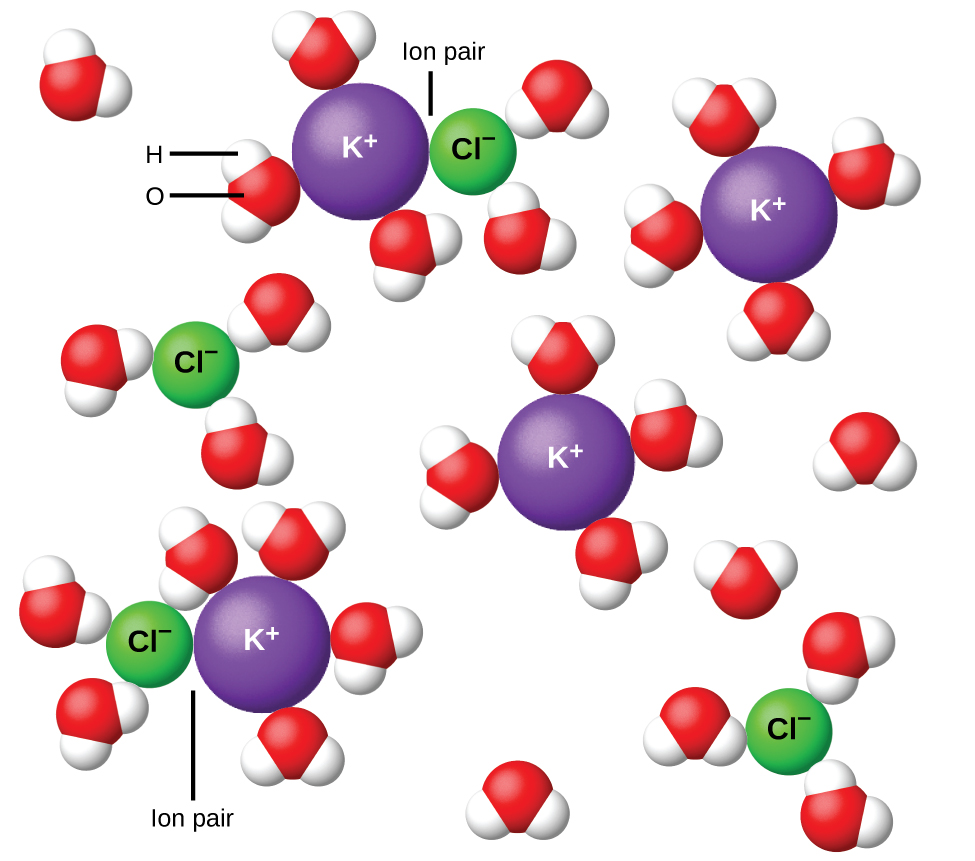
Resumo
As propriedades de uma solução que dependem apenas da concentração de partículas de soluto são chamadas de propriedades coligativas. Eles incluem mudanças na pressão de vapor, no ponto de ebulição e no ponto de congelamento do solvente na solução. As magnitudes dessas propriedades dependem apenas da concentração total de partículas de soluto na solução, não do tipo de partículas. A concentração total de partículas de soluto em uma solução também determina sua pressão osmótica. Essa é a pressão que deve ser aplicada à solução para evitar a difusão de moléculas de solvente puro através de uma membrana semipermeável na solução. Os compostos iônicos podem não se dissociar completamente em solução devido aos efeitos da atividade; nesse caso, os efeitos coligativos observados podem ser menores do que o previsto.
Equações-chave
- \(\left(P_\ce{A}=X_\ce{A}P^\circ_\ce{A}\right)\)
- \(P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i\)
- \(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
- ΔT b = K b m
- ΔT f = K f m
- Π = MRT
Notas de pé
- Um não eletrólito mostrado para comparação.
Glossário
- elevação do ponto de ebu
- elevação do ponto de ebulição de um líquido pela adição de um soluto
- ponto de ebulição constante de
- a constante de proporcionalidade na equação que relaciona a elevação do ponto de ebulição à molalidade do soluto; também conhecida como constante ebullioscópica
- propriedade coligativa
- propriedade de uma solução que depende apenas da concentração de uma espécie de soluto
- creenação
- processo pelo qual as células biológicas ficam enrugadas devido à perda de água por osmose
- depressão do ponto de congelamento
- redução do ponto de congelamento de um líquido pela adição de um soluto
- constante de depressão do ponto de congelamento
- (também, constante crioscópica) constante de proporcionalidade na equação que relaciona a depressão do ponto de congelamento à molalidade do soluto
- hemólise
- ruptura dos glóbulos vermelhos devido ao acúmulo de excesso de água por osmose
- hipertônico
- de maior pressão osmótica
- hipotônico
- de menor pressão osmótica
- par de íons
- par ânion/cátion solvatado mantido unido por atração eletrostática moderada
- isotônico
- de igual pressão osmótica
- molalidade (mm)
- uma unidade de concentração definida como a razão entre o número de moles de soluto e a massa do solvente em quilogramas
- osmose
- difusão de moléculas de solvente através de uma membrana semipermeável
- pressão osmótica (Π)
- pressão oposta necessária para evitar a transferência em massa de moléculas de solvente através de uma membrana semipermeável
- Lei de Raoult
- a pressão parcial exercida por um componente da solução é igual ao produto da fração molar do componente na solução e sua pressão de vapor de equilíbrio no estado puro
- membrana semipermeável
- uma membrana que permite seletivamente a passagem de certos íons ou moléculas
- fator Ivan 't Hoff (i)
- a razão entre o número de moles de partículas em uma solução e o número de moles de unidades de fórmula dissolvidas na solução


