5.3: Entalpia

Last updated
Save as PDF

Page ID: 185443

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Declare a primeira lei da termodinâmica
Defina a entalpia e explique sua classificação como uma função de estado
Escreva e balanceie equações termoquímicas
Calcule as mudanças de entalpia para várias reações químicas
Explique a lei de Hess e use-a para calcular entalpias de reação

A termoquímica é um ramo da termodinâmica química, a ciência que lida com as relações entre calor, trabalho e outras formas de energia no contexto de processos químicos e físicos. Ao nos concentrarmos na termoquímica neste capítulo, precisamos considerar alguns conceitos de termodinâmica amplamente usados.

As substâncias agem como reservatórios de energia, o que significa que a energia pode ser adicionada a elas ou removida delas. A energia é armazenada em uma substância quando a energia cinética de seus átomos ou moléculas é aumentada. A maior energia cinética pode estar na forma de translações aumentadas (movimentos de viagem ou em linha reta), vibrações ou rotações dos átomos ou moléculas. Quando a energia térmica é perdida, as intensidades desses movimentos diminuem e a energia cinética diminui. O total de todos os tipos possíveis de energia presentes em uma substância é chamado de energia interna (U), às vezes simbolizada como E.

À medida que um sistema sofre uma mudança, sua energia interna pode mudar e a energia pode ser transferida do sistema para o ambiente ou do ambiente para o sistema. A energia é transferida para um sistema quando ele absorve calor (q) do ambiente ou quando o ambiente funciona (w) no sistema. Por exemplo, a energia é transferida para o fio de metal à temperatura ambiente se estiver imerso em água quente (o fio absorve o calor da água) ou se você dobrar rapidamente o fio para frente e para trás (o fio fica mais quente por causa do trabalho realizado nele). Ambos os processos aumentam a energia interna do fio, o que se reflete em um aumento na temperatura do fio. Por outro lado, a energia é transferida de um sistema quando o calor é perdido do sistema ou quando o sistema funciona nos arredores.

A relação entre energia interna, calor e trabalho pode ser representada pela equação:

\[ΔU=q+w \label{5.4.1} \]

conforme mostrado na Figura$\PageIndex{1}$. Esta é uma versão da primeira lei da termodinâmica e mostra que a energia interna de um sistema muda através do fluxo de calor para dentro ou para fora do sistema (q positivo é o fluxo de calor para dentro; q negativo é o fluxo de calor para fora) ou pelo trabalho realizado no ou pelo sistema. O trabalho, w, é positivo se for feito no sistema e negativo se for feito pelo sistema.

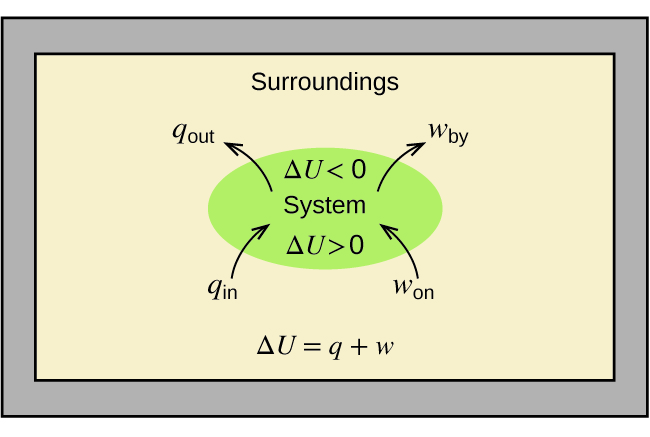
Figura$\PageIndex{1}$: A energia interna, U, de um sistema pode ser alterada pelo fluxo de calor e pelo trabalho. Se o calor fluir para o sistema, q _in, ou se o trabalho for feito no sistema, w _on, sua energia interna aumenta, ΔU > 0. Se o calor sair do sistema, q _sair ou o trabalho for feito pelo sistema, w _by, sua energia interna diminui, ΔU < 0.

Um tipo de trabalho chamado trabalho de expansão (ou trabalho de volume de pressão) ocorre quando um sistema empurra o ambiente contra uma pressão restritiva ou quando o ambiente comprime o sistema. Um exemplo disso ocorre durante a operação de um motor de combustão interna. A reação da gasolina e do oxigênio é exotérmica. Parte dessa energia é liberada como calor, e outra funciona empurrando o pistão no cilindro. As substâncias envolvidas na reação são o sistema, e o motor e o resto do universo são os arredores. O sistema perde energia ao aquecer e trabalhar no ambiente, e sua energia interna diminui. (O motor é capaz de manter o carro em movimento porque esse processo é repetido várias vezes por segundo enquanto o motor está funcionando.) Consideraremos como determinar a quantidade de trabalho envolvido em uma mudança química ou física no capítulo sobre termodinâmica.

Conforme discutido, a relação entre energia interna, calor e trabalho pode ser representada como ΔU = q + w. A energia interna é um tipo de quantidade conhecida como função de estado (ou variável de estado), enquanto calor e trabalho não são funções de estado. O valor de uma função de estado depende somente do estado em que o sistema se encontra e não de como esse estado é alcançado. Se uma quantidade não for uma função de estado, seu valor dependerá de como o estado é alcançado. Um exemplo de função de estado é altitude ou elevação. Se você estiver no cume do Monte. Kilimanjaro, você está a uma altitude de 5895 m, e não importa se você caminhou até lá ou caiu de paraquedas lá. A distância que você percorreu até o topo do Kilimanjaro, no entanto, não é uma função estatal. Você pode subir até o cume por uma rota direta ou por um caminho mais rotundo e tortuoso (Figura$\PageIndex{2}$). As distâncias percorridas seriam diferentes (a distância não é uma função estadual), mas a elevação alcançada seria a mesma (a altitude é uma função estadual).

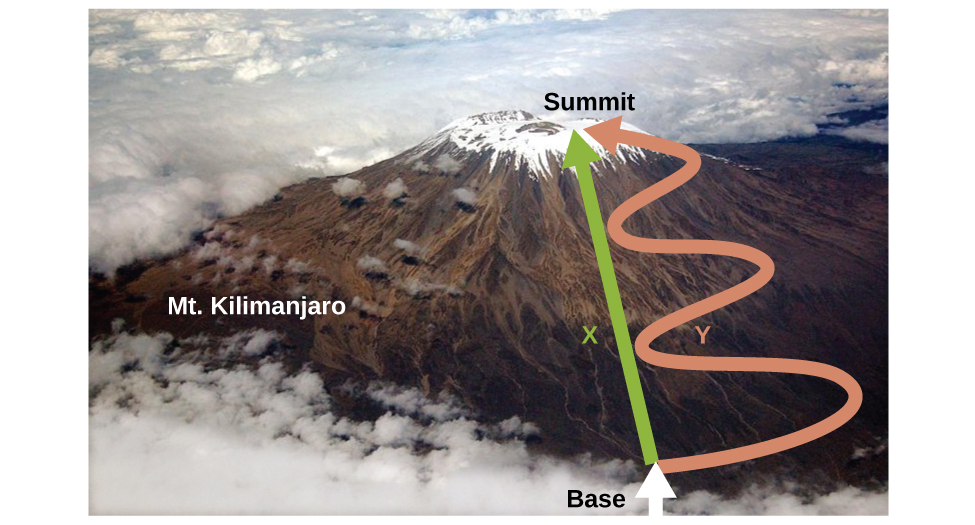
Figura$\PageIndex{2}$: Os caminhos X e Y representam duas rotas diferentes até o cume do Monte. Kilimanjaro. Ambos têm a mesma mudança de elevação (altitude ou elevação em uma montanha é uma função do estado; não depende do caminho), mas têm distâncias percorridas muito diferentes (a distância percorrida não é uma função estadual; depende do caminho). (crédito: modificação da obra de Paul Shaffner)

Os químicos normalmente usam uma propriedade conhecida como entalpia ($H$) para descrever a termodinâmica dos processos químicos e físicos. A entalpia é definida como a soma da energia interna de um sistema ($U$) e o produto matemático de sua pressão ($P$) e volume ($V$):

\[H=U+PV \label{5.4.2} \]

Como é derivada de três funções de estado ($U$$P$, e$V$), a entalpia também é uma função de estado. Os valores de entalpia para substâncias específicas não podem ser medidos diretamente; somente as alterações de entalpia para processos químicos ou físicos podem ser determinadas. Para processos que ocorrem em pressão constante (uma condição comum para muitas mudanças químicas e físicas), a mudança de entalpia ($ΔH$) é:

\[ΔH=ΔU+PΔV\label{5.4.3} \]

O produto matemático$PΔV$ representa trabalho ($w$), ou seja, trabalho de expansão ou volume de pressão, conforme observado. Por suas definições, os sinais aritméticos de ΔV e w sempre serão opostos:

\[PΔV=−w \label{5.4.4} \]

Substituindo a Equação\ ref {5.4.4} e a definição de energia interna (Equação\ ref {5.4.1}) na Equação\ ref {5.4.3} produz:

\[ \begin{align} ΔH&=ΔU+PΔV \\[4pt] &=q_\ce{p}+\cancel{w}−\cancel{w} \\[4pt] &=q_\ce{p} \label{5.4.5} \end{align} \]

onde$q_p$ está o calor da reação sob condições de pressão constante.

Portanto, se um processo químico ou físico for realizado em pressão constante com o único trabalho realizado causado por expansão ou contração, o fluxo de calor ($q_\ce{p}$) e a mudança de entalpia ($ΔH$) para o processo são iguais.

O calor emitido quando você opera um queimador de Bunsen é igual à mudança de entalpia da reação de combustão de metano que ocorre, pois ocorre na pressão essencialmente constante da atmosfera. Por outro lado, o calor produzido por uma reação medida em um calorímetro de bomba não é igual$ΔH$ porque o recipiente de metal fechado e de volume constante impede que o trabalho de expansão ocorra. Os químicos geralmente realizam experimentos em condições atmosféricas normais, com pressão externa constante com$q = ΔH$, o que torna a entalpia a escolha mais conveniente para determinar o calor.

As seguintes convenções se aplicam quando usamos$ΔH$:

Os químicos usam uma equação termoquímica para representar as mudanças na matéria e na energia. Em uma equação termoquímica, a mudança de entalpia de uma reação é mostrada como um valor de ΔH seguindo a equação da reação. Esse$ΔH$ valor indica a quantidade de calor associada à reação envolvendo o número de moles de reagentes e produtos, conforme mostrado na equação química. Por exemplo, considere esta equação:\[\ce{H2(g) + 1/2 O2(g) ⟶ H2O (l)} \;\; ΔH=\mathrm{−286\:kJ} \label{5.4.6} \] Essa equação indica que quando 1 mol de gás hidrogênio e 12 mol de gás oxigênio em alguma temperatura e pressão mudam para 1 mol de água líquida na mesma temperatura e pressão, 286 kJ de calor são liberados para o ambiente. Se os coeficientes da equação química forem multiplicados por algum fator, a mudança de entalpia deve ser multiplicada por esse mesmo fator (ΔH é uma propriedade extensa).

\[\begin {align*} &\textrm{(two-fold increase in amounts)}\label{5.4.7}\\ &\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\hspace{20px}ΔH=\mathrm{2×(−286\:kJ)=−572\:kJ}\\ &\textrm{(two-fold decrease in amounts)}\\ &\frac{1}{2}\ce{H2}(g)+\dfrac{1}{4}\ce{O2}(g)⟶\frac{1}{2}\ce{H2O}(l)\hspace{20px}ΔH=\mathrm{\frac{1}{2}×(−286\:kJ)=−143\:kJ} \end {align*} \label{5.4.6B} \]

A mudança de entalpia de uma reação depende do estado físico dos reagentes e produtos da reação (se temos gases, líquidos, sólidos ou soluções aquosas), portanto, eles devem ser mostrados. Por exemplo, quando 1 mol de gás hidrogênio e 12 mol de gás oxigênio mudam para 1 mol de água líquida na mesma temperatura e pressão, 286 kJ de calor são liberados. Se a água gasosa se formar, apenas 242 kJ de calor são liberados.

\[\ce{ H2(g) + 1/2 O2(g) ⟶ H2O(g)} \;\;\; ΔH=\ce{−242\:kJ} \label{5.4.7B} \]

Um valor negativo de uma alteração de entalpia, ΔH, indica uma reação exotérmica; um valor positivo de ΔH indica uma reação endotérmica. Se a direção de uma equação química for invertida, o sinal aritmético de seu ΔH é alterado (um processo endotérmico em uma direção é exotérmico na direção oposta).

Exemplo$\PageIndex{1}$: Measurement of an Enthalpy Change

Quando 0,0500 mol de HCl (aq) reage com 0,0500 mol de NaOH (aq) para formar 0,0500 mol de NaCl (aq), 2,9 kJ de calor são produzidos. O que é ΔH, a mudança de entalpia, por mol de reação ácida, para a reação ácido-base executada nas condições descritas?

\[\ce{HCl (aq) + NaOH(aq) \rightarrow NaCl (aq) + H2O(l)} \nonumber \]

Solução

Para a reação de 0,0500 mol de ácido (HCl), q = −2,9 kJ. Essa proporção

\[\mathrm{\dfrac{−2.9 \; kJ}{0.0500\; mol\; HCl}} \nonumber \]

pode ser usado como um fator de conversão para encontrar o calor produzido quando 1 mol de HCl reage:

\[ΔH =\mathrm{1\; \cancel{mol\; HCl} \times \dfrac{ −2.9\; kJ}{0.0500 \;\cancel{ mol\; HCl}} =−58\; kJ} \nonumber \]

A mudança de entalpia quando 1 mol de HCl reage é −58 kJ. Como esse é o número de moles na equação química, escrevemos a equação termoquímica como:

\[\ce{HCl}_{(aq)}+\ce{NaOH}_{(aq)}⟶\ce{NaCl}_{(aq)}+\ce{H_2O}_{(l)} \;\;\; ΔH=\mathrm{−58\;kJ} \nonumber \]

Exercício$\PageIndex{1}$

Quando 1,34 g de Zn (s) reage com 60,0 mL de 0,750 M HCl (aq), 3,14 kJ de calor são produzidos. Determine a mudança de entalpia por mol de zinco reagindo para a reação:

\[ \ce{Zn}_{(s)}+\ce{2HCl}_{(aq)}⟶\ce{ZnCl}_{(aq)}+\ce{H}_{2(g)} \nonumber \]

Resposta: ΔH = −153 kJ

Certifique-se de levar em consideração a estequiometria e os reagentes limitantes ao determinar o ΔH para uma reação química.

Exemplo$\PageIndex{2}$: Another Example of the Measurement of an Enthalpy Change

Um ursinho de goma contém 2,67 g de sacarose, C ₁₂ H ₂₂ O ₁₁. Quando reage com 7,19 g de clorato de potássio, KClO ₃, 43,7 kJ de calor são produzidos. Determine a mudança de entalpia para a reação

\[\ce{C12H22O11}(aq)+\ce{8KClO3}(aq)⟶\ce{12CO2}(g)+\ce{11H2O}(l)+\ce{8KCl}(aq) \nonumber \]

Solução SS

Temos$\mathrm{2.67\:\cancel{g}×\dfrac{1\:mol}{342.3\:\cancel{g}}=0.00780\:mol\:C_{12}H_{22}O_{11}}$ disponível, e

$\mathrm{7.19\:\cancel{g}×\dfrac{1\:mol}{122.5\:\cancel{g}}=0.0587\:mol\:KClO_3}$disponível.

Desde

$\mathrm{0.0587\:mol\:KClO_3×\dfrac{1\:mol\:\ce{C12H22O11}}{8\:mol\:KClO_3}=0.00734\:mol\:\ce{C12H22O11}}$

é necessário, C ₁₂ H ₂₂ O ₁₁ é o excesso de reagente e KClO ₃ é o reagente limitante.

A reação usa 8 mol KClO ₃, e o fator de conversão é$\mathrm{\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}}$, então nós temos$ΔH=\mathrm{8\:mol×\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}=−5960\:kJ}$. A mudança de entalpia para essa reação é −5960 kJ, e a equação termoquímica é:

\[\ce{C12H22O11 + 8KClO3⟶12CO2 + 11H2O + 8KCl}\hspace{20px}ΔH=\ce{−5960\:kJ} \nonumber \]

Exercício$\PageIndex{2}$

Quando 1,42 g de ferro reage com 1,80 g de cloro, 3,22 g$\ce{FeCl}_{2(s)}$ e 8,60 kJ de calor são produzidos. Qual é a mudança de entalpia para a reação quando 1 mol de$\ce{FeCl2(s)}$ é produzido?

Resposta: ΔH = −38 kJ

As alterações de entalpia são normalmente tabuladas para reações nas quais os reagentes e os produtos estão nas mesmas condições. Um estado padrão é um conjunto comumente aceito de condições usado como ponto de referência para a determinação de propriedades sob outras condições diferentes. Para químicos, o estado padrão da IUPAC se refere a materiais sob pressão de 1 bar e soluções a 1 M e não especifica uma temperatura (também é usado). Muitas tabelas termoquímicas listam valores com um estado padrão de 1 atm. Como o ΔH de uma reação muda muito pouco com essas pequenas mudanças na pressão (1 bar = 0,987 atm), os valores de ΔH (exceto para os valores medidos com maior precisão) são essencialmente os mesmos em ambos os conjuntos de condições padrão. Incluiremos um “o” sobrescrito no símbolo de mudança de entalpia para designar o estado padrão. Como a temperatura usual (mas não tecnicamente padrão) é 298,15 K, usaremos um “298” subscrito para designar essa temperatura. Assim, o símbolo ($ΔH^\circ_{298}$) é usado para indicar uma mudança de entalpia para um processo que ocorre nessas condições. (O símbolo ΔH é usado para indicar uma mudança de entalpia para uma reação que ocorre em condições não padronizadas.)

As mudanças de entalpia para muitos tipos de processos químicos e físicos estão disponíveis na literatura de referência, incluindo aquelas para reações de combustão, transições de fase e reações de formação. Ao discutirmos essas quantidades, é importante prestar atenção à natureza extensiva das alterações de entalpia e entalpia. Como a mudança de entalpia para uma determinada reação é proporcional às quantidades de substâncias envolvidas, ela pode ser relatada nessa base (ou seja, como o ΔH para quantidades específicas de reagentes). No entanto, muitas vezes achamos mais útil dividir uma propriedade extensa (ΔH) por outra (quantidade de substância) e relatar um valor intensivo por quantidade de ΔH, geralmente “normalizado” para uma base por mol. (Observe que isso é semelhante a determinar o calor específico da propriedade intensiva a partir da extensa capacidade de calor da propriedade, conforme visto anteriormente.)

Entalpia da combustão

A entalpia padrão da combustão (n$ΔH_C^\circ$) é a mudança de entalpia quando 1 mol de uma substância queima (combina vigorosamente com o oxigênio) sob condições de estado padrão; às vezes é chamada de “calor de combustão”. Por exemplo, a entalpia da combustão do etanol, −1366,8 kJ/mol, é a quantidade de calor produzida quando um mol de etanol sofre combustão completa a 25 °C e pressão de 1 atmosfera, produzindo produtos também a 25 °C e 1 atm.

\[\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}+\ce{3H2O}(l)\hspace{20px}ΔH_{298}^\circ=\mathrm{−1366.8\: kJ} \label{5.4.8} \]

As entalpias de combustão de muitas substâncias foram medidas; algumas delas estão listadas na Tabela$\PageIndex{1}$. Muitas substâncias prontamente disponíveis com grandes entalpias de combustão são usadas como combustíveis, incluindo hidrogênio, carbono (como carvão ou carvão vegetal) e hidrocarbonetos (compostos contendo apenas hidrogênio e carbono), como metano, propano e os principais componentes da gasolina.

Tabela$\PageIndex{1}$: Entalpias molares padrão de combustão
Substância	Reação de combustão	Entalpia da combustão$ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)$
carbono	$\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−393.5
hidrogênio	$\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−285.8
magnésio	$\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−601.6
enxofre	$\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−296.8
monóxido de carbono	$\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−283.0
metano	$\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−890.8
acetileno	$\ce{C2H2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{2CO2}(g)+\ce{H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−1301.1
etanol	$\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−1366.8
metanol	$\ce{CH3OH}(l)+\dfrac{3}{2}\ce{O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−726.1
isooctano	$\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)$	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−5461

Exemplo$\PageIndex{3}$: Using Enthalpy of Combustion

Como$\PageIndex{3}$ sugere a Figura, a combustão da gasolina é um processo altamente exotérmico. Vamos determinar a quantidade aproximada de calor produzida pela queima de 1,00 L de gasolina, supondo que a entalpia da combustão da gasolina seja a mesma do isooctano, um componente comum da gasolina. A densidade do isooctano é de 0,692 g/mL.

Figura$\PageIndex{3}$: A combustão da gasolina é muito exotérmica. (crédito: modificação do trabalho por “AlexEagle” /Flickr)

Solução

Começando com uma quantidade conhecida (1,00 L de isooctano), podemos realizar conversões entre unidades até chegarmos à quantidade desejada de calor ou energia. A entalpia da combustão do isooctano fornece uma das conversões necessárias. A tabela$\PageIndex{1}$ fornece esse valor como −5460 kJ por 1 mol de isooctano (C ₈ H ₁₈).

Usando esses dados,

\[\mathrm{1.00\:\cancel{L\:\ce{C8H18}}×\dfrac{1000\:\cancel{mL\:\ce{C8H18}}}{1\:\cancel{L\:\ce{C8H18}}}×\dfrac{0.692\:\cancel{g\:\ce{C8H18}}}{1\:\cancel{mL\:\ce{C8H18}}}×\dfrac{1\:\cancel{mol\:\ce{C8H18}}}{114\:\cancel{g\:\ce{C8H18}}}×\dfrac{−5460\:kJ}{1\:\cancel{mol\:\ce{C8H18}}}=−3.31×10^4\:kJ} \nonumber \]

A combustão de 1,00 L de isooctano produz 33.100 kJ de calor. (Essa quantidade de energia é suficiente para derreter 99,2 kg, ou cerca de 218 libras, de gelo.)

Nota: Se você fizer esse cálculo uma etapa por vez, encontrará:

\ (\ begin {align*}
&\ mathrm {1,00\ :L\:\ ce {C8H18} 1,00×10^3\ :mL\:\ ce {C8H18}}\\
&\ mathrm {1,00×10^3\ :mL\:\ ce {C8H18} 692\ :g\:\ ce {C8H18}}\
&\ mathrm {692\ :g\:\ ce {C8H18} 6,07\ :mol\:\ ce {C8H18}}\\
&\ mathrm {692\ :g\:\ ce {C8H18} −3,31×10^4\ :kJ}
\ end {align*}\)

Exercício$\PageIndex{3}$

Quanto calor é produzido pela combustão de 125 g de acetileno?

Resposta: 6,25 × 10 ³ kJ

Tecnologias energéticas emergentes baseadas em algas (biocombustíveis)

À medida que as reservas de combustíveis fósseis diminuem e se tornam mais caras de extrair, a busca continua por fontes de combustível substitutas para o futuro. Entre os biocombustíveis mais promissores estão os derivados de algas (Figura$\PageIndex{4}$). As espécies de algas usadas são atóxicas, biodegradáveis e estão entre os organismos que mais crescem no mundo. Cerca de 50% do peso das algas é óleo, que pode ser facilmente convertido em combustível, como biodiesel. As algas podem produzir 26.000 galões de biocombustível por hectare — muito mais energia por acre do que outras culturas. Algumas cepas de algas podem florescer em água salobra que não é utilizável para o cultivo de outras culturas. As algas podem produzir biodiesel, biogasolina, etanol, butanol, metano e até combustível de aviação.

Figura$\PageIndex{4}$: (a) Pequenos organismos de algas podem ser (b) cultivados em grandes quantidades e, eventualmente, (c) transformados em um combustível útil, como o biodiesel. (crédito a: modificação da obra de Micah Sittig; crédito b: modificação da obra de Robert Kerton; crédito c: modificação da obra de John F. Williams)

De acordo com o Departamento de Energia dos EUA, apenas 39.000 quilômetros quadrados (cerca de 0,4% da massa terrestre$\dfrac{1}{7}$ dos EUA ou menos da área usada para cultivar milho) podem produzir combustível de algas suficiente para substituir todo o combustível à base de petróleo usado nos EUA. O custo dos combustíveis para algas está se tornando mais competitivo — por exemplo, a Força Aérea dos EUA está produzindo combustível de aviação a partir de algas a um custo total de menos de $5 por galão. O processo usado para produzir combustível para algas é o seguinte: cultivar as algas (que usam a luz solar como fonte de energia e CO ₂ como matéria-prima); colher as algas; extrair os compostos de combustível (ou compostos precursores); processar conforme necessário (por exemplo, realizar uma reação de transesterificação para produzir biodiesel); purificar; e distribuir (Figura$\PageIndex{5}$).

Figura$\PageIndex{5}$: As algas convertem a luz solar e o dióxido de carbono em óleo que é colhido, extraído, purificado e transformado em uma variedade de combustíveis renováveis.

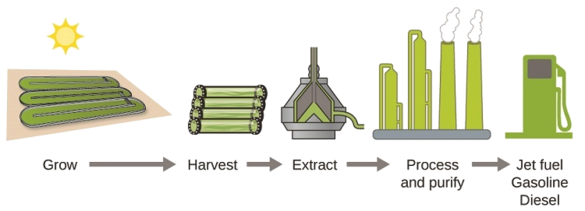
Entalpia de formação padrão

Uma entalpia padrão de formação$ΔH^\circ_\ce{f}$ é uma mudança de entalpia para uma reação na qual exatamente 1 mol de uma substância pura é formado a partir de elementos livres em seus estados mais estáveis sob condições de estado padrão. Esses valores são especialmente úteis para calcular ou prever mudanças de entalpia para reações químicas que são impraticáveis ou perigosas de realizar, ou para processos para os quais é difícil fazer medições. Se tivermos valores para as entalpias padrão de formação apropriadas, podemos determinar a mudança de entalpia para qualquer reação, que praticaremos na próxima seção sobre a lei de Hess.

A entalpia padrão de formação de CO ₂ (g) é −393,5 kJ/mol. Esta é a mudança de entalpia para a reação exotérmica:

\[\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=−393.5\:\ce{kJ} \label{5.4.9} \]

começando com os reagentes a uma pressão de 1 atm e 25 °C (com o carbono presente como grafite, a forma mais estável de carbono nessas condições) e terminando com um mol de CO ₂, também a 1 atm e 25 °C. Para o dióxido de nitrogênio,$\ce{NO}_{2(g)}$,$ΔH^\circ_\ce{f}$ é 33,2 kJ/mol. Esta é a mudança de entalpia da reação:

\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=+33.2\: \ce{kJ} \label{5.4.10} \]

Uma equação de reação com$\frac{1}{2}$ mol de N ₂ e 1 mol de O ₂ está correta neste caso porque a entalpia padrão de formação sempre se refere a 1 mol de produto, NO ₂ (g).

Você encontrará uma tabela de entalpias padrão de formação de muitas substâncias comuns nas Tabelas T1 e T2. Esses valores indicam que as reações de formação variam de altamente exotérmicas (como −2984 kJ/mol para a formação de P ₄ O ₁₀) a fortemente endotérmicas (como +226,7 kJ/mol para a formação de acetileno, C ₂ H ₂). Por definição, a entalpia padrão de formação de um elemento em sua forma mais estável é igual a zero em condições padrão, que é 1 atm para gases e 1 M para soluções.

Exemplo$\PageIndex{4}$: Evaluating an Enthalpy of Formation

O ozônio, O ₃ (g), se forma a partir do oxigênio, O ₂ (g), por um processo endotérmico. A radiação ultravioleta é a fonte da energia que impulsiona essa reação na alta atmosfera. Supondo que tanto os reagentes quanto os produtos da reação estejam em seus estados padrão, determine a entalpia padrão de formação$ΔH^\circ_\ce{f}$ do ozônio a partir das seguintes informações:

\[\ce{3O2}(g)⟶\ce{2O3}(g)\hspace{20px}ΔH^\circ_{298}=+286\: \ce{kJ} \nonumber \]

S olutio n$ΔH^\circ_\ce{f}$ é a mudança de entalpia para a formação de um mol de uma substância em seu estado padrão a partir dos elementos em seus estados padrão. Assim,$ΔH^\circ_\ce{f}$ para O ₃ (g) é a mudança de entalpia para a reação:

\[\dfrac{3}{2}\ce{O2}(g)⟶\ce{O3}(g) \nonumber \]

Para a formação de 2 mol de O ₃ (g),$ΔH^\circ_{298}=+286\: \ce{kJ}$. Essa proporção,$\mathrm{\left(\dfrac{286\:kJ}{2\:mol\:O_3}\right)}$, pode ser usada como um fator de conversão para encontrar o calor produzido quando 1 mol de O ₃ (g) é formado, que é a entalpia de formação para O ₃ (g):

\[ΔH^\circ \ce{\:for\:1\:mole\: of\:O_3}(g)=\mathrm{1\:\cancel{mol\:O_3}×\dfrac{286\:kJ}{2\:\cancel{mol\:O_3}}=143\:kJ} \nonumber \]

Portanto,$ΔH^\circ_\ce{f}[\ce{O3}(g)]=\ce{+143\: kJ/mol}$.

Exercício$\PageIndex{4}$

O gás hidrogênio, H ₂, reage explosivamente com o cloro gasoso, Cl ₂, para formar cloreto de hidrogênio, HCl (g). Qual é a mudança de entalpia para a reação de 1 mol de H ₂ (g) com 1 mol de Cl ₂ (g) se os reagentes e os produtos estiverem em condições de estado padrão? A entalpia padrão de formação de HCl (g) é −92,3 kJ/mol.

Resposta

Para a reação

\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{298}=\mathrm{−184.6\:kJ} \nonumber \]

Exemplo$\PageIndex{5}$: Writing Reaction Equations for $ΔH^\circ_\ce{f}$

Escreva as equações da reação de calor de formação para:

$\ce{C2H_5OH}_{(l)}$
$\ce{Ca_3(PO_4)}_{2(s)}$

Solução

Lembrando que as equações de$ΔH^\circ_\ce{f}$ reação servem para formar 1 mol do composto a partir de seus elementos constituintes sob condições padrão, temos:

$\ce{2C}(s,\:\ce{graphite})+\ce{3H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OH}(l)$
$\ce{3Ca}(s)+\frac{1}{2}\ce{P4}(s)+\ce{4O2}(g)⟶\ce{Ca3(PO4)2}(s)$

Nota: O estado padrão do carbono é grafite, e o fósforo existe como$P_4$.

Exercício$\PageIndex{5}$

Escreva as equações da reação de calor de formação para:

$\ce{C_2H_5OC_2H}_{5(l)}$
$\ce{Na_2CO}_{3(s)}$

Responda a: $\ce{4C}(s,\:\ce{graphite})+\ce{5H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OC2H5}(l)$;
Resposta b: $\ce{2Na}(s)+\ce{C}(s,\:\ce{graphite})+\dfrac{3}{2}\ce{O2}(g)⟶\ce{Na2CO3}(s)$

Lei de Hess

Há duas maneiras de determinar a quantidade de calor envolvida em uma mudança química: medi-la experimentalmente ou calculá-la a partir de outras mudanças de entalpia determinadas experimentalmente. Algumas reações são difíceis, se não impossíveis, de investigar e fazer medições precisas experimentalmente. E mesmo quando uma reação não é difícil de realizar ou medir, é conveniente poder determinar o calor envolvido em uma reação sem precisar realizar um experimento.

Esse tipo de cálculo geralmente envolve o uso da lei de Hess, que afirma: Se um processo pode ser escrito como a soma de vários processos graduais, a mudança de entalpia do processo total é igual à soma das mudanças de entalpia das várias etapas. A lei de Hess é válida porque a entalpia é uma função de estado: as mudanças de entalpia dependem apenas de onde um processo químico começa e termina, mas não do caminho que ele percorre do início ao fim. Por exemplo, podemos pensar na reação do carbono com o oxigênio para formar dióxido de carbono como ocorrendo diretamente ou por um processo de duas etapas. O processo direto está escrito:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)}\;\;\;ΔH^∘_{298}=\mathrm{−394\;kJ} \label{ 5.4.11} \]

No processo de duas etapas, o primeiro monóxido de carbono é formado:

\[\ce{C}_{(s)}+\dfrac{1}{2}\ce{O}_{2(g)}⟶\ce{CO}_{(g)}\;\;\;ΔH^∘_{298}=\mathrm{−111\;kJ} \label{ 5.4.12} \]

Então, o monóxido de carbono reage ainda mais para formar dióxido de carbono:

\[\ce{CO} {(g)}+\dfrac{1}{2}\ce{O2}(g)⟶\ce{CO}_2 {(g)}\;\;\;ΔH^∘_{298}=\mathrm{−283\;kJ} \label{ 5.4.13} \]

A equação que descreve a reação geral é a soma dessas duas mudanças químicas:

\[\begin {align*} &\textrm{Step 1:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)\\ &\underline{\textrm{Step 2:} \:\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)}\\ &\textrm{Sum:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)+\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)+\ce{CO2}(g) \end {align*} \label{5.4.14} \]

Como o CO produzido na Etapa 1 é consumido na Etapa 2, a variação líquida é:

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)} \label{5.4.15} \]

De acordo com a lei de Hess, a mudança de entalpia da reação será igual à soma das mudanças de entalpia das etapas. Podemos aplicar os dados das entalpias experimentais de combustão na Tabela$\PageIndex{1}$ para encontrar a mudança de entalpia de toda a reação em suas duas etapas:

\ [\ begin {align*}
&\ ce {C} (s) +\ frac {1} {2}\ ce {O2} (g) ⟶\ ce {CO} (g) &&ΔH^\ circ_ {298} =\ mathrm {−111\ :kJ}\\
&\ ce {CO} (g) +\ frac {1} {2}\ ce {OJ}\\ &\ ce {CO} (g) +\ frac {1} {2}\ ce {O2} 2} (g) ⟶\ ce {CO2} (g) &&ΔH^\ circ_ {298} =\ mathrm {−283\ :kJ}\\
&\ sobrelinha {\ ce {C} (s) +\ ce {O2} (g) ⟶\ ce {CO2} (g)\ hspace {25px}} & ; &\ overline {ΔH^\ circ_ {298} =\ mathrm {−394\ :kJ}}
\ end {align*}\ label {5.4.16}\]

O resultado é mostrado na Figura$\PageIndex{6}$. Vemos que ΔH da reação geral é o mesmo, independentemente de ocorrer em uma ou duas etapas. Essa descoberta (ΔH geral para a reação = soma dos valores de ΔH para as “etapas” da reação na reação geral) é verdadeira em geral para processos químicos e físicos.

Figura$\PageIndex{6}$: A formação de CO ₂ (g) a partir de seus elementos pode ser considerada como ocorrendo em duas etapas, que somam a reação geral, conforme descrito pela lei de Hess. As linhas azuis horizontais representam entalpias. Para um processo exotérmico, os produtos têm menor entalpia do que os reagentes.

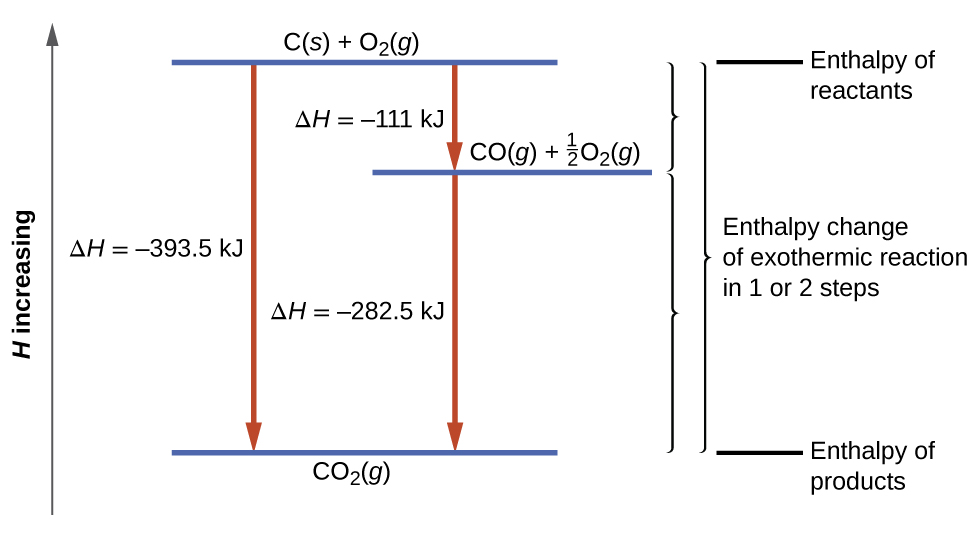
Antes de praticarmos ainda mais o uso da lei de Hess, lembremos duas características importantes de ΔH.

ΔH é diretamente proporcional às quantidades de reagentes ou produtos. Por exemplo, a mudança de entalpia para a reação formando 1 mol de NO ₂ (g) é +33,2 kJ:\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{+33.2\: kJ} \label{5.4.17} \]
Quando 2 moles de NO ₂ (o dobro) são formados, o ΔH será duas vezes maior:\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g)\hspace{20px}ΔH=\mathrm{+66.4\: kJ} \label{5.4.18} \]

Em geral, se multiplicarmos ou dividirmos uma equação por um número, a mudança de entalpia também deve ser multiplicada ou dividida pelo mesmo número.
ΔH para uma reação em uma direção é igual em magnitude e oposto em sinal a ΔH para a reação na direção inversa. Por exemplo, considerando que:\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH=\mathrm{−184.6\:kJ} \label{5.4.19} \]
Então, para a reação “reversa”, a mudança de entalpia também é “revertida”:\[\ce{2HCl}(g)⟶\ce{H2}(g)+\ce{Cl2}(g)\hspace{20px}ΔH=\mathrm{+184.6\: kJ} \label{5.4.20} \]

Exemplo$\PageIndex{6}$: Stepwise Calculation of $ΔH^\circ_\ce{f}$

Usando a Lei de Hess Determine a entalpia de formação,$ΔH^\circ_\ce{f}$, de FeCl ₃ (s) a partir das mudanças de entalpia do seguinte processo de duas etapas que ocorre sob condições de estado padrão:

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{20px}ΔH°=\mathrm{−341.8\:kJ} \nonumber \]

\[\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm \nonumber{−57.7\:kJ} \nonumber \]

Solução

Estamos tentando encontrar a entalpia padrão de formação de FeCl3 (s), que é igual a ΔH° para a reação:

\[\ce{Fe}(s)+\frac{3}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH^\circ_\ce{f}=\:? \nonumber \]

Observando as reações, vemos que a reação para a qual queremos encontrar ΔH° é a soma das duas reações com valores conhecidos de ΔH, então devemos somar seus ΔH s:

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{59px}ΔH°=\mathrm{−341.8\:kJ}\\ \underline{\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm{−57.7\:kJ}}\\ \ce{Fe}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{43px}ΔH°=\mathrm{−399.5\:kJ} \nonumber \]

A entalpia de formação,$ΔH^\circ_\ce{f}$, de FeCl ₃ (s) é −399,5 kJ/mol.

Exercício$\PageIndex{6}$

Calcule ΔH para o processo:

\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g) \nonumber \]

a partir das seguintes informações:

\[\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g)\hspace{20px}ΔH=\mathrm{180.5\:kJ} \nonumber \]

\[\ce{NO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{−57.06\:kJ} \nonumber \]

Resposta: 6,4 kJ

Aqui está um exemplo menos direto que ilustra o processo de pensamento envolvido na solução de muitos problemas da lei de Hess. Mostra como podemos encontrar muitas entalpias padrão de formação (e outros valores de ΔH) se forem difíceis de determinar experimentalmente.

Exemplo$\PageIndex{7}$: A More Challenging Problem

Usando a Lei de Hess, o monofluoreto de cloro pode reagir com o flúor para formar trifluoreto de cloro:

(i)$\ce{ClF}(g)+\ce{F2}(g)⟶\ce{ClF3}(g)\hspace{20px}ΔH°=\:?$

Use as reações aqui para determinar o ΔH° para a reação (i):

(ii)$\ce{2OF2}(g)⟶\ce{O2}(g)+\ce{2F2}(g)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−49.4\:kJ}$

(iii)$\ce{2ClF}(g)+\ce{O2}(g)⟶\ce{Cl2O}(g)+\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{+205.6\: kJ}$

(iv)$\ce{ClF3}(g)+\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+266.7\: kJ}$

Solução

Nosso objetivo é manipular e combinar as reações (ii), (iii) e (iv) de forma que elas se somam à reação (i). Indo da esquerda para a direita em (i), vemos primeiro que$\ce{ClF}_{(g)}$ é necessário como reagente. Isso pode ser obtido multiplicando a reação (iii) por$\frac{1}{2}$, o que significa que a mudança de ΔH° também é multiplicada por$\frac{1}{2}$:

\[\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)\hspace{20px} ΔH°=\frac{1}{2}(205.6)=+102.8\: \ce{kJ} \nonumber \]

Em seguida, vemos que também$\ce{F_2}$ é necessário como reagente. Para obter isso, reverta e reduza pela metade a reação (ii), o que significa que o ΔH° muda de sinal e é reduzido pela metade:

\[\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)\hspace{20px}ΔH°=+24.7\: \ce{kJ} \nonumber \]

Para obter ClF ₃ como produto, inverta (iv), alterando o sinal de ΔH°:

\[\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)⟶\ce{ClF3}(g)+\ce{O2}(g)\hspace{20px}ΔH°=\mathrm{−266.7\: kJ} \nonumber \]

Agora, verifique se essas reações correspondem à reação que queremos:

\ [\ begin {align*}
&\ ce {ClF} (g) +\ frac {1} {2}\ ce {O2} (g) ⟶\ frac {1} {2}\ ce {Cl2O} (g) +\ frac {1} {2}\ ce {OF2} (g) &&ΔH°=\ mathrm {+102.8\: kJ}\\
&\ frac {1} {2}\ ce {O2} (g) +\ ce {F2} (g) ⟶\ ce {OF2} (g) &&ΔH°=\ mathrm {+24,7\: kJ}\\
&\ frac {1} {2}\ ce {Cl2O} (g) +\ dfrac {3} {2}\ ce {OF2} (g) ⟶\ ce {ClF3} (g) +\ ce {O2} (g) &&ΔH°=\ mathrm {−266,7\ :kJ}\\
&\ sobrelinha {\ ce {ClF} (g) +\ ce {F2} ⟶\ ce {ClF3} (g)\ hspace {130px}} &&\ over linha {ΔH°=\ mathrm {−139.2\ :kJ}}
\ end {align*}\ nonumber\]

Reagentes$\frac{1}{2}\ce{O2}$ e$\frac{1}{2}\ce{O2}$ cancelam o produto O ₂; o produto$\frac{1}{2}\ce{Cl2O}$ cancela o reagente$\frac{1}{2}\ce{Cl2O}$; e o reagente$\dfrac{3}{2}\ce{OF2}$ é cancelado pelos produtos$\frac{1}{2}\ce{OF2}$ e OF ₂. Isso deixa apenas os reagentes ClF (g) e F ₂ (g) e o produto ClF ₃ (g), que são o que queremos. Como a soma dessas três reações modificadas produz a reação de interesse, a soma dos três valores modificados de ΔH° produzirá o ΔH° desejado:

$ΔH°=\mathrm{(+102.8\:kJ)+(24.7\:kJ)+(−266.7\:kJ)=−139.2\:kJ}$

Exercício$\PageIndex{7}$

O cloreto de alumínio pode ser formado a partir de seus elementos:

(i)$\ce{2Al}(s)+\ce{3Cl2}(g)⟶\ce{2AlCl3}(s)\hspace{20px}ΔH°=\:?$

Use as reações aqui para determinar o ΔH° para a reação (i):

(ii)$\ce{HCl}(g)⟶\ce{HCl}(aq)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−74.8\:kJ}$

(iii)$\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{−185\:kJ}$

(iv)$\ce{AlCl3}(aq)⟶\ce{AlCl3}(s)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+323\:kJ/mol}$

(v)$\ce{2Al}(s)+\ce{6HCl}(aq)⟶\ce{2AlCl3}(aq)+\ce{3H2}(g)\hspace{20px}ΔH^\circ_{(v)}=\mathrm{−1049\:kJ}$

Resposta: −1407 kJ

Também podemos usar a lei de Hess para determinar a alteração da entalpia de qualquer reação se as entalpias correspondentes de formação dos reagentes e produtos estiverem disponíveis. As reações graduais que consideramos são: (i) decomposições dos reagentes em seus elementos componentes (para as quais as mudanças de entalpia são proporcionais ao negativo das entalpias de formação dos reagentes), seguidas por (ii) recombinações dos elementos para dar os produtos (com a entalpia mudanças proporcionais às entalpias de formação dos produtos). A mudança de entalpia padrão da reação geral é, portanto, igual a: (ii) a soma das entalpias padrão de formação de todos os produtos mais (i) a soma dos negativos das entalpias padrão de formação dos reagentes. Isso geralmente é reorganizado ligeiramente para ser escrito da seguinte forma,$\sum$ representando “a soma de” e n representando os coeficientes estequiométricos:

\[ΔH^\circ_\ce{reaction}=\sum n×ΔH^\circ_\ce{f}\ce{(products)}−\sum n×ΔH^\circ_\ce{f}\ce{(reactants)} \label{5.4.20B} \]

O exemplo a seguir mostra em detalhes por que essa equação é válida e como usá-la para calcular a mudança de entalpia para uma reação de interesse.

Exemplo$\PageIndex{8}$: Using Hess’s Law

Qual é a mudança de entalpia padrão para a reação:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\hspace{20px}ΔH°=\:? \nonumber \]

Solução 1: Usando a equação

Como alternativa, poderíamos usar a forma especial da lei de Hess dada anteriormente:

\[ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)} \nonumber \]

\[\begin {align*} &=\mathrm{\left[2\:\cancel{mol\:HNO_3}×\dfrac{−207.4\:kJ}{\cancel{mol\:HNO_3\:(\mathit{aq})}}+1\:\cancel{mol\: NO\:(\mathit{g})}×\dfrac{+90.2\: kJ}{\cancel{mol\: NO\:(\mathit{g})}}\right]}\\ &\mathrm{\:−\,\left[3\:\cancel{mol\:NO_2(\mathit{g})}×\dfrac{+33.2\: kJ}{\cancel{mol\:NO_2\:(\mathit{g})}}+1\:\cancel{mol\:H_2O\:(\mathit{l})}×\dfrac{−285.8\:kJ}{\cancel{mol\:H_2O\:(\mathit{l})}}\right]}\\ &=\mathrm{2(−207.4\:kJ)+1(+90.2\: kJ)−3(+33.2\: kJ)−1(−285.8\:kJ)}\\ &=\mathrm{−138.4\:kJ}\end {align*} \nonumber \]

Solução 2: Apoiando por que a equação geral é válida

Podemos escrever essa reação como a soma das decomposições de 3NO ₂ (g) e 1H ₂ O (l) em seus elementos constituintes e a formação de 2 HNO ₃ (aq) e 1 NO (g) a partir de seus elementos constituintes. Escrevendo essas reações e observando suas relações com os$ΔH^\circ_\ce{f}$ valores desses compostos (das Tabelas T1 e T2), temos:

\[\ce{3NO2}(g)⟶ \dfrac{3}{2} \ce{N2}(g)+ 3 \ce{O2}(g)\hspace{20px}ΔH^\circ_{1}=\mathrm{−99.6\:kJ} \nonumber \]

\[\ce{H2O}(l)⟶\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)\hspace{20px}ΔH^\circ_{2}=+285.8\: \ce{kJ}\:[−1×ΔH^\circ_\ce{f}(\ce{H2O})] \nonumber \]

\[\ce{H2}(g)+\ce{N2}(g)+ 3 \ce{O2}(g)⟶\ce{2HNO3}(aq)\hspace{20px}ΔH^\circ_{3}=−414.8\:kJ\:[2×ΔH^\circ_\ce{f}(\ce{HNO3 \nonumber})] \nonumber \]

\[\frac{1}{2}\ce{N2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO}(g)\hspace{20px}ΔH^\circ \nonumber_{4}=+90.2\: \ce{kJ}\:[1×(\ce{NO})] \nonumber \]

A soma dessas equações de reação fornece a reação em que estamos interessados:

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g) \nonumber \]

A soma de suas mudanças de entalpia fornece o valor que queremos determinar:

\[\begin {align*} ΔH^\circ_\ce{rxn}&=ΔH^\circ_1+ΔH^\circ_2+ΔH^\circ_3+ΔH^\circ_4=\mathrm{(−99.6\:kJ)+(+285.8\: kJ)+(−414.8\:kJ)+(+90.2\: kJ)}\\ &=\mathrm{−138.4\:kJ} \end {align*} \nonumber \]

Portanto, a mudança de entalpia padrão para essa reação é ΔH° = −138,4 kJ.

Observe que esse resultado foi obtido por:

multiplicando o$ΔH^\circ_\ce{f}$ de cada produto pelo seu coeficiente estequiométrico e somando esses valores,
multiplicando o$ΔH^\circ_\ce{f}$ de cada reagente por seu coeficiente estequiométrico e somando esses valores, e então
subtraindo o resultado encontrado na etapa 2 do resultado encontrado na etapa 1.

Esse também é o procedimento para usar a equação geral, conforme mostrado.

Exercício$\PageIndex{8}$

Calcule o calor de combustão de 1 mol de etanol, C ₂ H ₅ OH (l), quando H ₂ O (l) e CO ₂ (g) são formados. Use as seguintes entalpias de formação: C ₂ H ₅ OH (l), −278 kJ/mol; H ₂ O (l), −286 kJ/mol; e CO ₂ (g), −394 kJ/mol.

Resposta: −1368 kJ/mol

Resumo

Se uma mudança química é realizada em pressão constante e o único trabalho realizado é causado por expansão ou contração, q para a mudança é chamado de mudança de entalpia com o símbolo ΔH, ou$ΔH^\circ_{298}$ para reações que ocorrem sob condições de estado padrão. O valor de ΔH para uma reação em uma direção é igual em magnitude, mas oposto em sinal, a ΔH para a reação na direção oposta, e ΔH é diretamente proporcional à quantidade de reagentes e produtos. Exemplos de mudanças de entalpia incluem entalpia de combustão, entalpia de fusão, entalpia de vaporização e entalpia padrão de formação. A entalpia padrão de formação,$ΔH^\circ_\ce{f}$, é a mudança de entalpia que acompanha a formação de 1 mol de uma substância a partir dos elementos em seus estados mais estáveis a 1 bar (estado padrão). Muitos dos processos são realizados a 298,15 K. Se as entalpias de formação estiverem disponíveis para os reagentes e produtos de uma reação, a mudança de entalpia pode ser calculada usando a lei de Hess: Se um processo pode ser escrito como a soma de vários processos graduais, a mudança de entalpia do processo total é igual à soma das mudanças de entalpia das várias etapas.

Equações-chave

$ΔU=q+w$
$ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}$

Notas de pé

1 Para obter mais informações sobre o combustível de algas, consulte www.theguardian.com/environme... n-fuel-problem.

Glossário

termodinâmica química: área da ciência que lida com as relações entre calor, trabalho e todas as formas de energia associadas a processos químicos e físicos

entalpia (H): soma da energia interna de um sistema e o produto matemático de sua pressão e volume

alteração de entalpia (ΔH): calor liberado ou absorvido por um sistema sob pressão constante durante um processo químico ou físico

trabalho de expansão (trabalho de volume de pressão): trabalho realizado à medida que um sistema se expande ou se contrai contra a pressão externa

primeira lei da termodinâmica: a energia interna de um sistema muda devido ao fluxo de calor dentro ou fora do sistema ou ao trabalho realizado no ou pelo sistema

Lei de Hess: se um processo pode ser representado como a soma de várias etapas, a mudança de entalpia do processo é igual à soma das mudanças de entalpia das etapas

hidrocarbonetos: composto apenas de hidrogênio e carbono; o principal componente dos combustíveis fósseis

energia interna (U): total de todos os tipos possíveis de energia presentes em uma substância ou substâncias

entalpia padrão de combustão ($ΔH^\circ_\ce{c}$): calor liberado quando um mol de um composto sofre combustão completa sob condições padrão

entalpia padrão de formação ($ΔH^\circ_\ce{f}$): alteração de entalpia de uma reação química na qual 1 mol de uma substância pura é formado a partir de seus elementos em seus estados mais estáveis sob condições de estado padrão

estado padrão: conjunto de condições físicas aceitas como condições de referência comuns para relatar propriedades termodinâmicas; 1 bar de pressão e soluções em concentrações de 1 molar, geralmente a uma temperatura de 298,15 K
função de estado: propriedade que depende apenas do estado de um sistema, e não do caminho percorrido para chegar a esse estado

Solução

Solução SS

Exemplo\(\PageIndex{3}\): Using Enthalpy of Combustion

Solução

Exercício\(\PageIndex{3}\)

Tecnologias energéticas emergentes baseadas em algas (biocombustíveis)

Exemplo\(\PageIndex{4}\): Evaluating an Enthalpy of Formation

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)

Solução

Exercício\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\): Stepwise Calculation of \(ΔH^\circ_\ce{f}\)

Solução

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{7}\): A More Challenging Problem

Solução

Exercício\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\): Using Hess’s Law

Solução 1: Usando a equação

Solução 2: Apoiando por que a equação geral é válida

Exercício\(\PageIndex{8}\)

Equações-chave

Substância	Reação de combustão	Entalpia da combustão\(ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)\)
carbono	\(\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−393.5
hidrogênio	\(\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−285.8
magnésio	\(\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−601.6
enxofre	\(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−296.8
monóxido de carbono	\(\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−283.0
metano	\(\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−890.8
acetileno	\(\ce{C2H2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{2CO2}(g)+\ce{H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−1301.1
etanol	\(\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−1366.8
metanol	\(\ce{CH3OH}(l)+\dfrac{3}{2}\ce{O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−726.1
isooctano	\(\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)\)	\ (ΔH_c^\ circ\ left (\ mathrm {\ dfrac {kJ} {mol}\ :a\ :25°C}\ right)\)” style="text-align:center; ">−5461

Objetivos de

Exemplo\(\PageIndex{1}\): Measurement of an Enthalpy Change

Solução

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\): Another Example of the Measurement of an Enthalpy Change

Solução SS

Exercício\(\PageIndex{2}\)

Entalpia da combustão

Exemplo\(\PageIndex{3}\): Using Enthalpy of Combustion

Solução

Exercício\(\PageIndex{3}\)

Tecnologias energéticas emergentes baseadas em algas (biocombustíveis)

Entalpia de formação padrão

Exemplo\(\PageIndex{4}\): Evaluating an Enthalpy of Formation

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)

Solução

Exercício\(\PageIndex{5}\)

Lei de Hess

Exemplo\(\PageIndex{6}\): Stepwise Calculation of \(ΔH^\circ_\ce{f}\)

Solução

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{7}\): A More Challenging Problem

Solução

Exercício\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\): Using Hess’s Law

Solução 1: Usando a equação

Solução 2: Apoiando por que a equação geral é válida

Exercício\(\PageIndex{8}\)

Resumo

Equações-chave

Notas de pé

Glossário