5.2: Calorimetria

Objetivos de

• Explicar a técnica da calorimetria
• Calcule e interprete o calor e propriedades relacionadas usando dados típicos de calorimetria

Uma técnica que podemos usar para medir a quantidade de calor envolvida em um processo químico ou físico é conhecida como calorimetria. A calorimetria é usada para medir quantidades de calor transferidas de ou para uma substância. Para isso, o calor é trocado por um objeto calibrado (calorímetro). A mudança na temperatura da parte de medição do calorímetro é convertida na quantidade de calor (já que a calibração anterior foi usada para estabelecer sua capacidade térmica). A medição da transferência de calor usando essa abordagem requer a definição de um sistema (a substância ou substâncias que sofrem alterações químicas ou físicas) e seus arredores (os outros componentes do aparelho de medição que servem para fornecer calor ao sistema ou absorva o calor do sistema). O conhecimento da capacidade térmica do ambiente e as medições cuidadosas das massas do sistema e do ambiente e suas temperaturas antes e depois do processo permitem calcular o calor transferido conforme descrito nesta seção.

Um calorímetro é um dispositivo usado para medir a quantidade de calor envolvida em um processo químico ou físico. Por exemplo, quando ocorre uma reação exotérmica em solução em um calorímetro, o calor produzido pela reação é absorvido pela solução, o que aumenta sua temperatura. Quando ocorre uma reação endotérmica, o calor necessário é absorvido pela energia térmica da solução, o que diminui sua temperatura (Figura\(\PageIndex{1}\)). A mudança de temperatura, junto com o calor e a massa específicos da solução, podem então ser usados para calcular a quantidade de calor envolvida em qualquer um dos casos.

Figura\(\PageIndex{1}\): Em uma determinação calorimétrica, ou (a) ocorre um processo exotérmico e o calor, q, é negativo, indicando que a energia térmica é transferida do sistema para seu entorno, ou (b) ocorre um processo endotérmico e o calor, q, é positivo, indicando que a energia térmica é transferida do entorno ao sistema.

Dois diagramas rotulados a e b são mostrados. Cada um é composto por dois recipientes retangulares com um termômetro inserido no canto superior direito e estendendo-se para dentro. Há uma seta voltada para a direita conectando cada caixa em cada diagrama. O recipiente esquerdo no diagrama a mostra uma solução rodopiante rosa e verde com os termos “Processo exotérmico” e “Sistema” escritos no centro com setas voltadas para longe dos termos apontando para “q”. Os rótulos “Solução” e “Ambiente” estão escritos na parte inferior do recipiente. O recipiente certo no diagrama a tem o termo “Solução” escrito na parte inferior do recipiente e uma seta vermelha voltada para cima perto do termômetro com a frase “Temperatura aumentada” ao lado dele. Os redemoinhos rosa e verde são mais misturados neste recipiente. O recipiente esquerdo no diagrama b mostra uma solução rodopiante roxa e azul com os termos “Processo endotérmico” e “Sistema” escritos no centro com setas voltadas para longe dos termos e “Solução” e “Ambiente” escritos na parte inferior. As setas apontam para longe da letra “q”. O recipiente direito no diagrama b tem o termo “Solução” escrito na parte inferior e uma seta vermelha voltada para baixo perto do termômetro com a frase “Temperatura diminuída” ao lado dele. Os redemoinhos azul e roxo são mais misturados neste recipiente.

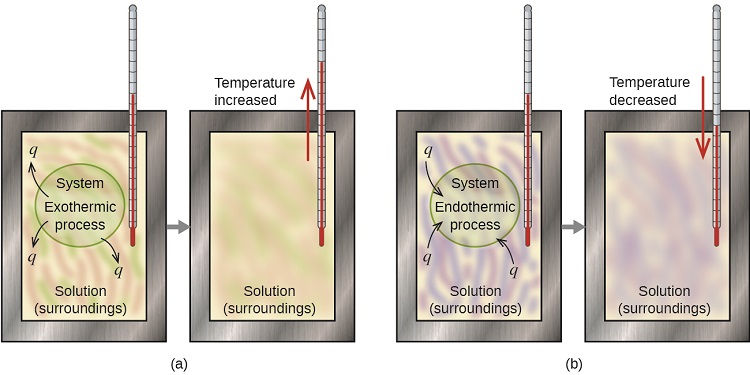
Por convenção, q recebe um sinal negativo (-) quando o sistema libera calor para o ambiente (exotérmico); q recebe um sinal positivo (+) quando o sistema absorve calor do ambiente (endotérmico).

Os cientistas usam calorímetros bem isolados que praticamente impedem a transferência de calor entre o calorímetro e seu ambiente. Isso permite a determinação precisa do calor envolvido nos processos químicos, do conteúdo energético dos alimentos e assim por diante. Estudantes de química geral costumam usar calorímetros simples construídos com copos de poliestireno (Figura\(\PageIndex{2}\)). Esses calorímetros de “xícara de café” fáceis de usar permitem mais troca de calor com o ambiente e, portanto, produzem valores de energia menos precisos.

Figura\(\PageIndex{2}\): Um calorímetro simples pode ser construído a partir de dois copos de poliestireno. Um termômetro e um agitador se estendem pela tampa até a mistura de reação.

Dois copos de isopor são mostrados aninhados um no outro com uma tampa na parte superior. Um termômetro e uma vareta de agitação são inseridos através da tampa e na solução dentro do copo, que é mostrada como um corte. A haste de agitação tem uma seta de duas pontas ao lado, voltada para cima e para baixo. A mistura líquida dentro do copo é rotulada como “Mistura de reação”.

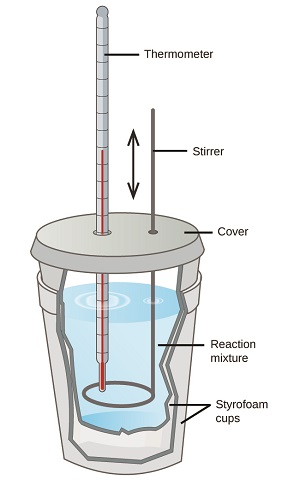
Calorímetros de soluções comerciais também estão disponíveis. Calorímetros relativamente baratos geralmente consistem em dois copos de paredes finas que são encaixados de forma a minimizar o contato térmico durante o uso, junto com uma tampa isolada, agitador portátil e termômetro simples. Os calorímetros mais caros usados na indústria e na pesquisa geralmente têm um recipiente de reação bem isolado e totalmente fechado, mecanismo de agitação motorizado e um sensor de temperatura mais preciso (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Os calorímetros de soluções comerciais variam de (a) modelos simples e baratos para uso por estudantes a (b) modelos caros e mais precisos para a indústria e pesquisa.

Dois diagramas são mostrados e rotulados a e b. O diagrama a mostra um termômetro que passa por uma tampa isolante em forma de disco e entra em um cilindro de metal que é rotulado como “recipiente interno de metal”, que por sua vez está aninhado em um cilindro de metal rotulado como “recipiente externo de metal”. O cilindro interno repousa sobre um anel de suporte isolante. Um agitador passa pela tampa isolante e também entra no cilindro interno. O diagrama b mostra um recipiente interno de metal meio cheio de líquido apoiado em um anel de suporte isolante e aninhado em um recipiente externo de metal. Uma sonda de temperatura de precisão e uma haste de agitação motorizada são colocadas na solução no recipiente interno e conectadas por fios ao equipamento externo à configuração.

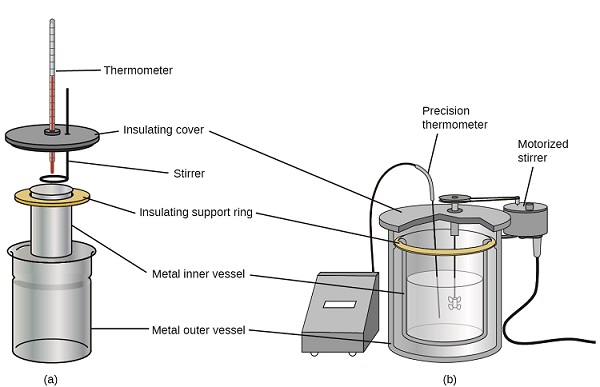
Antes de praticarmos problemas de calorimetria envolvendo reações químicas, considere um exemplo simples que ilustra a ideia central por trás da calorimetria. Suponha que inicialmente tenhamos uma substância de alta temperatura, como um pedaço de metal quente (M), e uma substância de baixa temperatura, como água fria (W). Se colocarmos o metal na água, o calor fluirá de M para W. A temperatura de M diminuirá e a temperatura de W aumentará, até que as duas substâncias tenham a mesma temperatura, ou seja, quando atingirem o equilíbrio térmico (Figura\(\PageIndex{4}\)). Se isso ocorrer em um calorímetro, o ideal é que toda essa transferência de calor ocorra entre as duas substâncias, sem ganho ou perda de calor pelo calorímetro ou pelo ambiente do calorímetro. Sob essas circunstâncias ideais, a mudança líquida de calor é zero:

\[q_\mathrm{\,substance\: M} + q_\mathrm{\,substance\: W}=0 \label{5.3.1} \]

Essa relação pode ser reorganizada para mostrar que o calor ganho pela substância M é igual ao calor perdido pela substância W:

\[q_\mathrm{\,substance\: M}=-q_\mathrm{\,substance\: W} \label{5.3.2} \]

A magnitude do calor (mudança) é, portanto, a mesma para ambas as substâncias, e o sinal negativo apenas mostra que\(q_{substance\, M}\) e\(q_{substance\, W}\) são opostos na direção do fluxo de calor (ganho ou perda), mas não indica o sinal aritmético de nenhum dos valores q (que é determinado pelo fato de o a matéria em questão ganha ou perde calor, por definição). Na situação específica descrita,\(q_{substance\, M}\) é um valor negativo e\(q_{substance\, W}\) é positivo, pois o calor é transferido de M para W.

Figura\(\PageIndex{4}\): Em um processo simples de calorimetria, (a) o calor, q, é transferido do metal quente, M, para a água fria, W, até que (b) ambos estejam na mesma temperatura.

Dois diagramas são mostrados e rotulados a e b. Cada diagrama é composto por um recipiente retangular com um termômetro inserido no interior a partir do canto superior direito. Ambos os contêineres são conectados por uma seta voltada para a direita. Ambos os recipientes estão cheios de água, representada pela letra “W”, e cada recipiente tem um quadrado no meio que representa um metal rotulado com a letra “M”. No diagrama a, o metal é desenhado em marrom e tem três flechas voltadas para o outro lado. Cada seta tem a letra “q” em sua extremidade. O metal é rotulado como “sistema” e a água é rotulada como “ambiente”. O termômetro neste diagrama tem uma leitura relativamente baixa. No diagrama b, o metal é representado em roxo e o termômetro tem uma leitura relativamente alta.

Exemplo\(\PageIndex{1}\): Heat Transfer between Substances at Different Temperatures

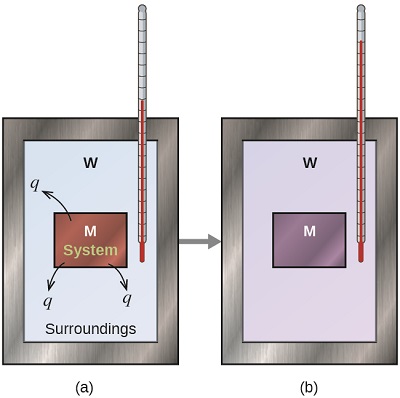
Um pedaço de vergalhão quente de 360 g (uma haste de aço usada para reforçar o concreto) é jogado em 425 mL de água a 24,0 °C. A temperatura final da água é medida como 42,7 °C. Calcule a temperatura inicial da peça de vergalhão. Suponha que o calor específico do aço seja aproximadamente o mesmo do ferro (Tabela T4) e que toda a transferência de calor ocorra entre o vergalhão e a água (não há troca de calor com o ambiente).

Solução

A temperatura da água aumenta de 24,0° C para 42,7° C, então a água absorve o calor. Esse calor veio do pedaço de vergalhão, que inicialmente estava em uma temperatura mais alta. Supondo que toda a transferência de calor fosse entre o vergalhão e a água, sem “perda” de calor para o ambiente, o calor liberado pelo vergalhão = − calor absorvido pela água, ou:

\[q_\ce{rebar}=−q_\ce{water} \nonumber \]

Como sabemos como o calor está relacionado a outras quantidades mensuráveis, temos:

\[(c×m×ΔT)_\ce{rebar}=−(c×m×ΔT)_\ce{water} \nonumber \]

Deixando f = final e i = inicial, na forma expandida, isso se torna:

\[ c_\ce{rebar}×m_\ce{rebar}×(T_\mathrm{f,rebar}−T_\mathrm{i,rebar})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]

A densidade da água é 1,0 g/mL, então 425 mL de água = 425 g. Observando que a temperatura final do vergalhão e da água é de 42,7° C, a substituição dos valores conhecidos produz:

\[ \mathrm{(0.449\:J/g\: °C)(360g)(42.7°C−\mathit T_\mathrm{i,rebar})=-(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)} \nonumber \]

\[\mathrm{\mathit T_{i,rebar}=\dfrac{(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)}{(0.449\:J/g\: °C)(360\:g)}+42.7°C} \nonumber \]

Resolver isso dá Ti, vergalhão = 248° C, então a temperatura inicial do vergalhão foi de 248° C.

Exercício\(\PageIndex{1A}\)

Um pedaço de cobre de 248 g é jogado em 390 mL de água a 22,6 °C. A temperatura final da água foi medida como 39,9 °C. Calcule a temperatura inicial da peça de cobre. Suponha que toda transferência de calor ocorra entre o cobre e a água.

Responda

A temperatura inicial do cobre foi de 335,6 °C.

Exercício\(\PageIndex{1B}\)

Um pedaço de cobre de 248 g inicialmente a 314 °C é jogado em 390 mL de água inicialmente a 22,6 °C. Supondo que toda a transferência de calor ocorra entre o cobre e a água, calcule a temperatura final.

Responda

A temperatura final (alcançada pelo cobre e pela água) é 38,7 °C.

Esse método também pode ser usado para determinar outras quantidades, como o calor específico de um metal desconhecido.

Exemplo\(\PageIndex{2}\): Identifying a Metal by Measuring Specific Heat

Um pedaço de metal de 59,7 g que havia sido submerso em água fervente foi rapidamente transferido para 60,0 mL de água inicialmente a 22,0 °C. A temperatura final é 28,5 °C. Use esses dados para determinar o calor específico do metal. Use esse resultado para identificar o metal.

Solução

Assumindo uma transferência de calor perfeita, calor liberado pelo metal = −calor absorvido pela água, ou:

\[q_\ce{metal}=−q_\ce{water} \nonumber \]

Na forma expandida, isso é:

\[c_\ce{metal}×m_\ce{metal}×(T_\mathrm{f,metal}−T_\mathrm{i, metal})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]

Observando que, como o metal estava submerso em água fervente, sua temperatura inicial era de 100,0 °C; e que para a água, 60,0 mL = 60,0 g; temos:

\[\mathrm{(\mathit c_{metal})(59.7\:g)(28.5°C−100.0°C)=−(4.18\:J/g\: °C)(60.0\:g)(28.5°C−22.0°C)} \nonumber \]

Resolvendo isso:

\[\mathrm{\mathit c_{metal}=\dfrac{−(4.184\:J/g\: °C)(60.0\:g)(6.5°C)}{(59.7\:g)(−71.5°C)}=0.38\:J/g\: °C} \nonumber \]

Comparando isso com os valores na Tabela T4, nosso calor específico experimental está mais próximo do valor do cobre (0,39 J/g° C), então identificamos o metal como cobre.

Exercício\(\PageIndex{2}\)

Uma peça de 92,9 g de metal prateado/cinza é aquecida a 178,0 °C e, em seguida, rapidamente transferida para 75,0 mL de água inicialmente a 24,0 °C. Após 5 minutos, tanto o metal quanto a água atingem a mesma temperatura: 29,7 °C. Determine o calor específico e a identidade do metal. (Nota: Você deve descobrir que o calor específico é próximo ao de dois metais diferentes. Explique como você pode determinar com confiança a identidade do metal).

Responda

\(c_{metal}= 0.13 \;J/g\; °C\)

Esse calor específico é próximo ao do ouro ou do chumbo. Seria difícil determinar qual metal esse era baseado apenas nos valores numéricos. No entanto, a observação de que o metal é prateado/cinza, além do valor do calor específico, indica que o metal é chumbo.

 

Quando usamos a calorimetria para determinar o calor envolvido em uma reação química, os mesmos princípios que discutimos se aplicam. A quantidade de calor absorvida pelo calorímetro geralmente é pequena o suficiente para que possamos negligenciá-la (embora não para medições altamente precisas, conforme discutido posteriormente), e o calorímetro minimiza a troca de energia com o ambiente. Como a energia não é criada nem destruída durante uma reação química, não há mudança geral de energia durante a reação. O calor produzido ou consumido na reação (o “sistema”), _reação q, mais o calor absorvido ou perdido pela solução (o “ambiente”)\(q_{solution}\),, deve somar zero:

\[q_\ce{reaction}+q_\ce{solution}=0\ \label{ 5.3.10} \]

Isso significa que a quantidade de calor produzida ou consumida na reação é igual à quantidade de calor absorvida ou perdida pela solução:

\[q_\ce{reaction}=−q_\ce{solution} \label{5.3.11} \]

Esse conceito está no centro de todos os problemas e cálculos de calorimetria.

Exemplo\(\PageIndex{3}\): Heat Produced by an Exothermic Reaction

Quando 50,0 mL de 0,10 M de HCl (aq) e 50,0 mL de 1,00 M NaOH (aq), ambos a 22,0 °C, são adicionados a um calorímetro de xícara de café, a temperatura da mistura atinge um máximo de 28,9 °C. Qual é a quantidade aproximada de calor produzida por essa reação?

\[\ce{HCl}(aq)+\ce{NaOH}(aq)⟶\ce{NaCl}(aq)+\ce{H2O}(l) \nonumber \]

Solução SS

Para visualizar o que está acontecendo, imagine que você poderia combinar as duas soluções tão rapidamente que nenhuma reação ocorresse enquanto elas se misturavam; depois da mistura, a reação ocorreu. No momento da mistura, você tem 100,0 mL de uma mistura de HCl e NaOH a 22,0 °C. O HCl e o NaOH então reagem até que a temperatura da solução atinja 28,9 °C.

O calor liberado pela reação é igual ao absorvido pela solução. Portanto:

\[q_\ce{reaction}=−q_\ce{solution} \nonumber \]

(É importante lembrar que essa relação só se mantém se o calorímetro não absorver o calor da reação e não houver troca de calor entre o calorímetro e seus arredores.)

Em seguida, sabemos que o calor absorvido pela solução depende de sua mudança específica de calor, massa e temperatura:

\[q_\ce{solution}=(c×m×ΔT)_\ce{solution} \nonumber \]

Para prosseguir com esse cálculo, precisamos fazer mais algumas suposições ou aproximações razoáveis. Como a solução é aquosa, podemos proceder como se fosse água em termos de seus valores específicos de calor e massa. A densidade da água é de aproximadamente 1,0 g/mL, então 100,0 mL tem uma massa de cerca de 1,0 × 10 ² g (dois números significativos). O calor específico da água é de aproximadamente 4,18 J/g °C, então o usamos para o calor específico da solução. Substituindo esses valores, obtém-se:

\[\mathrm{\mathit q_{solution}=(4.184\:J/g\: °C)(1.0×10^2\:g)(28.9°C−22.0°C)=2.89×10^3\:J} \nonumber \]

Finalmente, como estamos tentando encontrar o calor da reação, temos:

\[q_\ce{reaction}=−q_\ce{solution}=−2.89×10^3\:J \nonumber \]

O sinal negativo indica que a reação é exotérmica. Ela produz 2,89 kJ de calor.

Exercício\(\PageIndex{3}\)

Quando 100 mL de NaCl 0,200 M (aq) e 100 mL de 0,200 M AgNO ₃ (aq), ambos a 21,9 °C, são misturados em um calorímetro de xícara de café, a temperatura aumenta para 23,5 °C à medida que o AgCl sólido se forma. Quanto calor é produzido por essa reação de precipitação? Quais suposições você fez para determinar seu valor?

Responda

\(1.34 \times 10^3\; J\); suponha que nenhum calor seja absorvido pelo calorímetro, nenhum calor seja trocado entre o calorímetro e seus arredores e que o calor e a massa específicos da solução sejam iguais aos da água

Termoquímica de aquecedores de mãos

Ao trabalhar ou brincar ao ar livre em um dia frio, você pode usar um aquecedor de mãos para aquecer as mãos (Figura\(\PageIndex{5}\)). Um aquecedor de mãos reutilizável comum contém uma solução supersaturada de NaC ₂ H ₃ O ₂ (acetato de sódio) e um disco de metal. Dobrar o disco cria locais de nucleação em torno dos quais o NaC ₂ H ₃ O ₂ metaestável se cristaliza rapidamente (um capítulo posterior sobre soluções investigará a saturação e a supersaturação com mais detalhes).

O processo\(\ce{NaC2H3O2}(aq)⟶\ce{NaC2H3O2}(s)\) é exotérmico e o calor produzido por esse processo é absorvido pelas mãos, aquecendo-as (pelo menos por um tempo). Se o aquecedor de mãos for reaquecido, o NaC ₂ H ₃ O ₂ se redissolverá e poderá ser reutilizado.

Figura\(\PageIndex{5}\): Aquecedores químicos para mãos produzem calor que aquece sua mão em um dia frio. Neste, você pode ver o disco de metal que inicia a reação exotérmica de precipitação. (crédito: modificação do trabalho da Science Buddies TV/YouTube)

Uma série de três fotos é mostrada. Há duas setas voltadas para a direita conectando uma foto à próxima. A primeira foto mostra um aquecedor químico de mãos. É uma bolsa que contém um líquido transparente e incolor. Há um disco branco localizado à direita dentro da bolsa. A segunda foto mostra a mesma coisa, exceto que o disco branco se tornou uma substância branca e turva. A terceira foto mostra a sacola inteira cheia dessa substância branca.

Outro aquecedor de mãos comum produz calor quando é aberto, expondo o ferro e a água do aquecedor de mãos ao oxigênio do ar. Uma versão simplificada dessa reação exotérmica é

\[\ce{2Fe(s) + 3/2 O2(g) ⟶ Fe2O3(s)}.\ n\nonumber \]

O sal no aquecedor de mãos catalisa a reação, por isso produz calor mais rapidamente; celulose, vermiculita e carvão ativado ajudam a distribuir o calor uniformemente. Outros tipos de aquecedores de mãos usam fluido mais leve (um catalisador de platina ajuda o fluido do isqueiro a oxidar exotérmicamente), carvão vegetal (o carvão oxida em um estojo especial) ou unidades elétricas que produzem calor ao passar uma corrente elétrica de uma bateria por fios resistivos.

Exemplo\(\PageIndex{4}\): Heat Flow in an Instant Ice Pack

Quando o nitrato de amônio sólido se dissolve na água, a solução fica fria. Essa é a base para uma “bolsa de gelo instantânea” (Figura\(\PageIndex{5}\)). Quando 3,21 g de NH ₄ NO ₃ sólido se dissolvem em 50,0 g de água a 24,9° C em um calorímetro, a temperatura diminui para 20,3° C.

Calcule o valor de q para essa reação e explique o significado de seu sinal aritmético. Declare todas as suposições que você fez.

Figura\(\PageIndex{5}\): Uma compressa fria instantânea consiste em uma bolsa contendo nitrato de amônio sólido e uma segunda bolsa de água. Quando o saco de água é quebrado, o pacote fica frio porque a dissolução do nitrato de amônio é um processo endotérmico que remove a energia térmica da água. A compressa fria então remove a energia térmica do seu corpo.

Solução

Assumimos que o calorímetro impede a transferência de calor entre a solução e seu ambiente externo (incluindo o próprio calorímetro), caso em que:

\[q_\ce{rxn}=−q_\ce{soln} \nonumber \]

com “rxn” e “soln” usados como abreviação para “reação” e “solução”, respectivamente.

Supondo também que o calor específico da solução seja o mesmo da água, temos:

\[\begin{align*} q_\ce{rxn} &=−q_\ce{soln}=−(c×m×ΔT)_\ce{soln}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(20.3°C−24.9°C)]}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(−4.6°C)]}\\ &+\mathrm{1.0×10^3\:J=+1.0\:kJ} \end{align*}\]

O sinal positivo para q indica que a dissolução é um processo endotérmico.

Exercício\(\PageIndex{4}\)

Quando uma amostra de 3,00 g de KCl foi adicionada a 3,00 × 10 ² g de água em um calorímetro de xícara de café, a temperatura diminuiu em 1,05 °C. Quanto calor está envolvido na dissolução do KCl? Quais suposições você fez?

Responda

1,33 kJ; suponha que o calorímetro impeça a transferência de calor entre a solução e seu ambiente externo (incluindo o próprio calorímetro) e que o calor específico da solução seja o mesmo da água.

Se a quantidade de calor absorvida por um calorímetro for muito grande para ser negligenciada ou se precisarmos de resultados mais precisos, devemos levar em consideração o calor absorvido pela solução e pelo calorímetro.

Figura\(\PageIndex{6}\): (a) Um calorímetro de bomba é usado para medir o calor produzido por reações envolvendo reagentes ou produtos gasosos, como combustão. (b) Os reagentes estão contidos na “bomba” estanque ao gás, que é submersa na água e cercada por materiais isolantes. (crédito a: modificação do trabalho por “Harbor1” /Wikimedia commons)

Uma imagem e um diagrama são mostrados, rotulados a e b, respectivamente. A imagem a mostra um calorímetro de bomba. É uma máquina em forma de cubo com uma cavidade na parte superior, um cilindro de metal acima da cavidade e um painel de leitura preso no lado superior direito. O diagrama b mostra uma figura recortada de um cubo com um recipiente cilíndrico cheio de água no meio dele. Outro recipiente, denominado “bomba”, fica dentro de um cilindro menor que contém um copo de amostra e está aninhado no recipiente cilíndrico cercado pela água. Uma linha preta se estende até a água e é rotulada como “Termômetro de precisão”. Dois fios denominados “Eletrodos” se estendem para longe de uma tampa que fica no topo do recipiente interno. Um painel de leitura está localizado no canto superior direito do cubo.

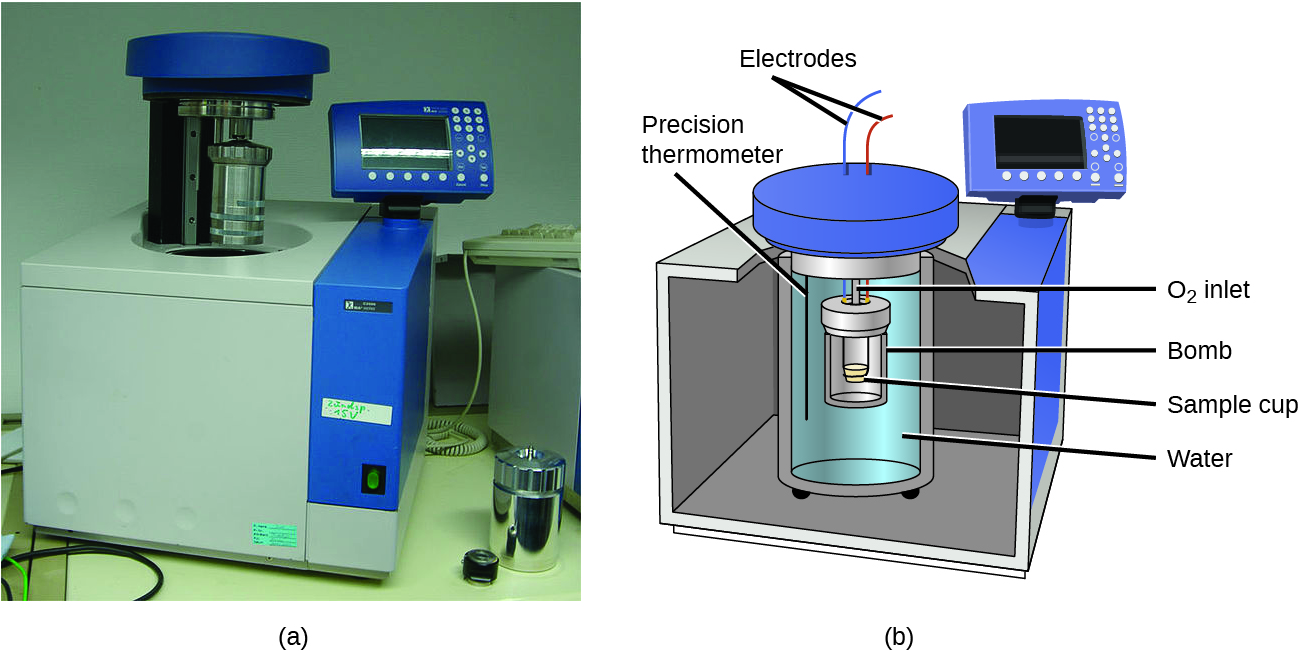
Os calorímetros descritos são projetados para operar em pressão constante (atmosférica) e são convenientes para medir o fluxo de calor que acompanha os processos que ocorrem na solução. Um tipo diferente de calorímetro que opera em volume constante, coloquialmente conhecido como calorímetro de bomba, é usado para medir a energia produzida por reações que produzem grandes quantidades de calor e produtos gasosos, como reações de combustão. (O termo “bomba” vem da observação de que essas reações podem ser vigorosas o suficiente para se assemelhar a explosões que danificariam outros calorímetros.) Esse tipo de calorímetro consiste em um recipiente de aço robusto (a “bomba”) que contém os reagentes e está submerso em água (Figura\(\PageIndex{6}\)). A amostra é colocada na bomba, que é então preenchida com oxigênio em alta pressão. Uma pequena faísca elétrica é usada para acender a amostra. A energia produzida pela reação fica presa na bomba de aço e na água ao redor. O aumento da temperatura é medido e, junto com a capacidade térmica conhecida do calorímetro, é usado para calcular a energia produzida pela reação. Os calorímetros de bomba requerem calibração para determinar a capacidade térmica do calorímetro e garantir resultados precisos. A calibração é realizada usando uma reação com um q conhecido, como uma quantidade medida de ácido benzóico inflamada por uma faísca de um fio fusível de níquel que é pesado antes e depois da reação. A mudança de temperatura produzida pela reação conhecida é usada para determinar a capacidade térmica do calorímetro. A calibração geralmente é realizada todas as vezes antes que o calorímetro seja usado para coletar dados de pesquisa.

Vídeo\(\PageIndex{1}\): Vídeo de como um calorímetro de bomba é preparado para a ação.

Exemplo\(\PageIndex{5}\): Bomb Calorimetry

Quando 3,12 g de glicose, C ₆ H ₁₂ O ₆, são queimados em um calorímetro de bomba, a temperatura do calorímetro aumenta de 23,8 °C para 35,6 °C. O calorímetro contém 775 g de água e a própria bomba tem uma capacidade térmica de 893 J/°C. Quanto calor foi produzido pelo combustão da amostra de glicose?

Solução

A combustão produz calor que é absorvido principalmente pela água e pela bomba. (As quantidades de calor absorvidas pelos produtos da reação e o excesso de oxigênio não reagido são relativamente pequenas e lidar com elas está além do escopo deste texto. Nós os negligenciaremos em nossos cálculos.)

O calor produzido pela reação é absorvido pela água e pela bomba:

\ [\ begin {align*}
&q_\ ce {rxn} =− (q_\ ce {água} +q_\ ce {bomba})\\
&=\ mathrm {− [(4.184\ :J/g\: °C) × (775\ :g) × (35,6°C−23,8°C) +893\ :J/°C× (35,6°C−23,8°C) +893\ :J/°C× (35,6°C−23,8°C) °C−23,8°C)]}\\
&=\ mathrm {− (38.300\ :J+10.500\ :J)}\\
&=\ mathrm {−48.800\: J=−48,8\: kJ}
\ end { alinhamento*}\ nonumber\]

Essa reação liberou 48,7 kJ de calor quando 3,12 g de glicose foram queimados.

Exercício\(\PageIndex{5}\)

Quando 0,963 g de benzeno, C ₆ H ₆, é queimado em um calorímetro de bomba, a temperatura do calorímetro aumenta em 8,39 °C. A bomba tem uma capacidade térmica de 784 J/°C e é submersa em 925 mL de água. Quanto calor foi produzido pela combustão da amostra de glicose?

Resposta

39,0 kJ

Desde que o primeiro foi construído em 1899, 35 calorímetros foram construídos para medir o calor produzido por uma pessoa viva. ¹ Esses calorímetros de corpo inteiro de vários designs são grandes o suficiente para acomodar um ser humano individual. Mais recentemente, os calorímetros de sala inteira permitem a realização de atividades relativamente normais, e esses calorímetros geram dados que refletem mais de perto o mundo real. Esses calorímetros são usados para medir o metabolismo de indivíduos sob diferentes condições ambientais, diferentes regimes alimentares e com diferentes condições de saúde, como diabetes. Em humanos, o metabolismo é normalmente medido em calorias por dia. Uma caloria nutricional (caloria) é a unidade de energia usada para quantificar a quantidade de energia derivada do metabolismo dos alimentos; uma caloria é igual a 1000 calorias (1 kcal), a quantidade de energia necessária para aquecer 1 kg de água em 1 °C.

Medindo calorias nutricionais

No seu dia-a-dia, você pode estar mais familiarizado com a energia fornecida em calorias, ou calorias nutricionais, que são usadas para quantificar a quantidade de energia nos alimentos. Uma caloria (cal) = exatamente 4,184 joules e uma caloria (observe a capitalização) = 1000 cal ou 1 kcal. (É aproximadamente a quantidade de energia necessária para aquecer 1 kg de água em 1 °C.)

Os macronutrientes dos alimentos são proteínas, carboidratos e gorduras ou óleos. As proteínas fornecem cerca de 4 calorias por grama, os carboidratos também fornecem cerca de 4 calorias por grama e as gorduras e os óleos fornecem cerca de 9 calorias/g. Os rótulos nutricionais das embalagens de alimentos mostram o conteúdo calórico de uma porção do alimento, bem como a decomposição em calorias de cada um dos três macronutrientes ( Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): (a) O macarrão e o queijo contêm energia na forma dos macronutrientes dos alimentos. (b) As informações nutricionais do alimento são mostradas no rótulo da embalagem. Nos EUA, o conteúdo energético é dado em calorias (por porção); o resto do mundo geralmente usa quilojoules. (crédito a: modificação da obra de “Rex Roof” /Flickr)

Para o exemplo mostrado em (b), a energia total por porção de 228 g é calculada por:

\[\mathrm{(5\:g\: protein×4\:Calories/g)+(31\:g\: carb×4\:Calories/g)+(12\:g\: fat×9\:Calories/g)=252\:Calories} \label{5.3.X} \]

Portanto, você pode usar rótulos de alimentos para contar suas calorias. Mas de onde vêm os valores? E quão precisos eles são? O conteúdo calórico dos alimentos pode ser determinado usando calorimetria de bomba; ou seja, queimando o alimento e medindo a energia que ele contém. Uma amostra de alimento é pesada, misturada no liquidificador, liofilizada, moída até virar pó e transformada em uma pastilha. O pellet é queimado dentro de um calorímetro de bomba e a mudança de temperatura medida é convertida em energia por grama de alimento.

Hoje, o conteúdo calórico nos rótulos dos alimentos é derivado usando um método chamado sistema Atwater, que usa o conteúdo calórico médio dos diferentes constituintes químicos dos alimentos, proteínas, carboidratos e gorduras. As quantidades médias são aquelas dadas na equação e são derivadas dos vários resultados obtidos pela calorimetria de bomba de alimentos integrais. A quantidade de carboidratos é descontada em uma certa quantidade pelo conteúdo de fibra, que é um carboidrato indigestível. Para determinar o conteúdo energético de um alimento, as quantidades de carboidratos, proteínas e gorduras são multiplicadas pela média de calorias por grama de cada um e pelos produtos somados para obter a energia total.

Resumo

A calorimetria é usada para medir a quantidade de energia térmica transferida em um processo químico ou físico. Isso requer uma medição cuidadosa da mudança de temperatura que ocorre durante o processo e das massas do sistema e dos arredores. Essas quantidades medidas são então usadas para calcular a quantidade de calor produzida ou consumida no processo usando relações matemáticas conhecidas. Os calorímetros são projetados para minimizar a troca de energia entre o sistema que está sendo estudado e seus arredores. Eles variam de calorímetros simples para xícaras de café usados por estudantes introdutórios de química a sofisticados calorímetros de bomba usados para determinar o conteúdo energético dos alimentos.

Notas de pé

1. 1 Francis D. Reardon e cols.. “O calorímetro humano Snellen revisitado, reprojetado e atualizado: características de design e desempenho.” Engenharia Médica e Biológica e Computação 8 (2006) 721—28, O calorímetro humano Snellen revisitado, reprojetado e atualizado: características de design e desempenho [link.springer.com].

Glossário

calorímetro de bomba

dispositivo projetado para medir a mudança de energia para processos que ocorrem sob condições de volume constante; comumente usado para reações envolvendo reagentes ou produtos sólidos e gasosos

calorímetro

dispositivo usado para medir a quantidade de calor absorvida ou liberada em um processo químico ou físico

calorimetria

processo de medição da quantidade de calor envolvida em um processo químico ou físico

caloria nutricional (caloria)

unidade usada para quantificar a energia fornecida pela digestão de alimentos, definida como 1000 cal ou 1 kcal

arredores

toda a matéria, exceto o sistema que está sendo estudado

sistema

porção de matéria passando por uma mudança química ou física sendo estudada