1.6: Tratamento matemático dos resultados de medição
- Page ID
- 185213
₽
- Explique a abordagem de análise dimensional (rótulo fatorial) para cálculos matemáticos envolvendo quantidades.
- Descreva como usar a análise dimensional para realizar conversões de unidades para uma determinada propriedade e cálculos envolvendo duas ou mais propriedades.
- Converta entre as três unidades principais de temperatura: Fahrenheit, Celsius e Kelvin.
Geralmente, uma quantidade de juros pode não ser fácil (ou mesmo possível) de medir diretamente, mas deve ser calculada a partir de outras propriedades medidas diretamente e relações matemáticas apropriadas. Por exemplo, considere medir a velocidade média de um atleta correndo sprints. Isso normalmente é feito medindo o tempo necessário para o atleta correr da linha de partida até a linha de chegada e a distância entre essas duas linhas e, em seguida, computando a velocidade a partir da equação que relaciona essas três propriedades:
\[\mathrm{speed=\dfrac{distance}{time}} \nonumber \]
Um velocista com qualidade olímpica pode correr 100 m em aproximadamente 10 s, correspondendo a uma velocidade média de
\[\mathrm{\dfrac{100\: m}{10\: s}=10\: m/s} \nonumber \]
Observe que essa aritmética simples envolve dividir os números de cada quantidade medida para produzir o número da quantidade calculada (100/10 = 10) e, da mesma forma, dividir as unidades de cada quantidade medida para produzir a unidade da quantidade calculada (m/s = m/s). Agora, considere usar essa mesma relação para prever o tempo necessário para uma pessoa correndo nessa velocidade percorrer uma distância de 25 m. A mesma relação entre as três propriedades é usada, mas neste caso, as duas quantidades fornecidas são uma velocidade (10 m/s) e uma distância (25 m). Para produzir a propriedade procurada, tempo, a equação deve ser reorganizada adequadamente:
\[\mathrm{time=\dfrac{distance}{speed}} \nonumber \]
O tempo pode então ser calculado como:
\[\mathrm{\dfrac{25\: m}{10\: m/s}=2.5\: s} \nonumber \]
Novamente, a aritmética dos números (25/10 = 2,5) foi acompanhada pela mesma aritmética nas unidades (m/m/s = s) para produzir o número e a unidade do resultado, 2,5 s. Observe que, assim como para os números, quando uma unidade é dividida por uma unidade idêntica (neste caso, m/m), o resultado é “1” —ou, como comumente formulado, as unidades” cancelar.”
Esses cálculos são exemplos de uma abordagem matemática versátil conhecida como análise dimensional (ou método de rótulo fatorial). A análise dimensional é baseada nessa premissa: as unidades de quantidades devem ser submetidas às mesmas operações matemáticas que seus números associados. Esse método pode ser aplicado a cálculos que variam de conversões de unidades simples a cálculos mais complexos de várias etapas envolvendo várias quantidades diferentes.
Fatores de conversão e análise dimensional
Uma proporção de duas quantidades equivalentes expressas com unidades de medida diferentes pode ser usada como um fator de conversão de unidade. Por exemplo, os comprimentos de 2,54 cm e 1 polegada são equivalentes (por definição) e, portanto, um fator de conversão unitário pode ser derivado da razão,
\[\mathrm{\dfrac{2.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: 2.54\:\dfrac{cm}{in.}} \nonumber \]
Vários outros fatores de conversão comumente usados são fornecidos na Tabela\(\PageIndex{1}\).
| Comprimento | Volume | Missa |
|---|---|---|
| 1 m = 1,0936 jardas | 1 L = 1,0567 qt | 1 kg = 2,2046 libras |
| 1 pol. = 2,54 cm (exato) | 1 qt = 0,94635 L | 1 lb = 453,59 g |
| 1 km = 0,62137 mi | 1 pé 3 = 28,317 L | 1 (avoirdupois) oz = 28,349 g |
| 1 mi = 1609,3 km | 1 colher de sopa = 14,787 mL | 1 onça (troy) = 31,103 g |
Quando multiplicamos uma quantidade (como a distância dada em polegadas) por um fator de conversão unitário apropriado, convertemos a quantidade em um valor equivalente com unidades diferentes (como a distância em centímetros). Por exemplo, o salto vertical de 34 polegadas de um jogador de basquete pode ser convertido em centímetros por:
\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm} \nonumber \]
Como essa aritmética simples envolve quantidades, a premissa da análise dimensional exige que multipliquemos números e unidades. Os números dessas duas quantidades são multiplicados para produzir o número da quantidade do produto, 86, enquanto as unidades são multiplicadas para produzir
\[\mathrm{\dfrac{in.\times cm}{in.}}. \nonumber \]
Assim como para números, uma proporção de unidades idênticas também é numericamente igual a um,
\[\mathrm{\dfrac{in.}{in.}=1} \nonumber \]
e o produto unitário, portanto, simplifica para cm. (Quando unidades idênticas se dividem para produzir um fator de 1, diz-se que elas “cancelam”.) Usando a análise dimensional, podemos determinar se um fator de conversão da unidade foi configurado corretamente, verificando se a unidade original será cancelada e o resultado conterá a unidade desejada (convertida).
A massa de um Frisbee de competição é 125 g. Converta sua massa em onças usando o fator de conversão unitário derivado da relação 1 oz = 28,349 g (Tabela\(\PageIndex{1}\)).
Solução
Se tivermos o fator de conversão, podemos determinar a massa em quilogramas usando uma equação semelhante à usada para converter o comprimento de polegadas para centímetros.
\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor}\nonumber \]
Escrevemos o fator de conversão da unidade em suas duas formas:
\[\mathrm{\dfrac{1\: oz}{28.349\: g}\:and\:\dfrac{28.349\: g}{1\: oz}}\nonumber \]
O fator de conversão unitário correto é a proporção que cancela as unidades de gramas e deixa onças.
\ [\ begin {align*}
x\:\ ce {oz} &=\ mathrm {125\:\ cancel {g}\ times\ dfrac {1\: oz} {28.349\:\ cancel {g}}\\
&=\ mathrm {\ left (\ dfrac {125} {28.349}\ right)\ :oz}\\
&=\ mathrm {4.41\: oz\: (três\: números\: significativos)}
\ end {align*}\ nonumber\]
Converta um volume de 9.345 qt em litros.
- Resposta
-
8.844 L
Além das simples conversões de unidades, o método fator-label pode ser usado para resolver problemas mais complexos envolvendo cálculos. Independentemente dos detalhes, a abordagem básica é a mesma — todos os fatores envolvidos no cálculo devem ser adequadamente orientados para garantir que seus rótulos (unidades) sejam cancelados e/ou combinados adequadamente para produzir a unidade desejada no resultado. É por isso que é chamado de método de rotulagem de fatores. À medida que seu estudo de química continua, você encontrará muitas oportunidades de aplicar essa abordagem.
Qual é a densidade do anticongelante comum em unidades de g/mL? Uma amostra de 4,00 qt do anticongelante pesa 9,26 lb.
Solução
Como isso\(\mathrm{density=\dfrac{mass}{volume}}\), precisamos dividir a massa em gramas pelo volume em mililitros. Em geral: o número de unidades de B = o número de unidades do fator de conversão da\(\times\) unidade A. Os fatores de conversão necessários são dados na Tabela 1.7.1:1 lb = 453,59 g; 1 L = 1,0567 qt; 1 L = 1.000 mL. Podemos converter massa de libras em gramas em uma única etapa:
\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{1\:\cancel{lb}}=4.20\times 10^3\:g}\nonumber \]
Precisamos usar duas etapas para converter o volume de quartos em mililitros.
- Converta quartos em litros.
\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: L}{1.0567\:\cancel{qt}}=3.78\: L}\nonumber \]
- Converta litros em mililitros.
\[\mathrm{3.78\:\cancel{L}\times\dfrac{1000\: mL}{1\:\cancel{L}}=3.78\times10^3\:mL}\nonumber \]
Então,
\[\mathrm{density=\dfrac{4.20\times10^3\:g}{3.78\times10^3\:mL}=1.11\: g/mL}\nonumber \]
Como alternativa, o cálculo pode ser configurado de uma forma que use três fatores de conversão de unidades sequencialmente, da seguinte forma:
\[\mathrm{\dfrac{9.26\:\cancel{lb}}{4.00\:\cancel{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\:\cancel{L}}{1000\: mL}=1.11\: g/mL}\nonumber \]
Qual é o volume em litros de 1.000 onças, considerando que 1 L = 1,0567 qt e 1 qt = 32 oz (exatamente)?
- Resposta
-
\(\mathrm{2.956\times10^{-2}\:L}\)
Enquanto estava sendo conduzido da Filadélfia para Atlanta, a uma distância de cerca de 1250 km, um Lamborghini Aventador Roadster 2014 usa 213 L de gasolina.
- Qual economia de combustível (média), em milhas por galão, o Roadster obteve durante essa viagem?
- Se a gasolina custa $3,80 por galão, qual foi o custo do combustível para essa viagem?
Solução
(a) Primeiro convertemos a distância de quilômetros para milhas:
\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi}\nonumber \]
e depois converta o volume de litros em galões:
\[\mathrm{213\:\cancel{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\: gal}{4\:\cancel{qt}}=56.3\: gal}\nonumber \]
Então,
\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg}\nonumber \]
Como alternativa, o cálculo pode ser configurado de uma forma que use todos os fatores de conversão sequencialmente, da seguinte forma:
\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{1\:\cancel{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg}\nonumber \]
(b) Usando o volume calculado anteriormente em galões, encontramos:
\[\mathrm{56.3\: gal\times\dfrac{$3.80}{1\: gal}=$214}\nonumber \]
Um Toyota Prius Hybrid usa 59,7 L de gasolina para dirigir de São Francisco a Seattle, a uma distância de 1300 km (dois dígitos significativos).
- Qual economia de combustível (média), em milhas por galão, o Prius obteve durante essa viagem?
- Se a gasolina custa $3,90 por galão, qual foi o custo do combustível para essa viagem?
- Responda a um
-
51 mpg
- Resposta b
-
$62
Conversão de unidades de temperatura
Usamos a palavra temperatura para nos referirmos ao calor ou ao frio de uma substância. Uma forma de medir uma mudança na temperatura é usar o fato de que a maioria das substâncias se expande quando a temperatura aumenta e se contrai quando a temperatura diminui. O mercúrio ou álcool em um termômetro de vidro comum muda seu volume à medida que a temperatura muda. Como o volume do líquido muda mais do que o volume do vidro, podemos ver o líquido se expandir quando esquenta e se contrair quando fica mais frio.
Para marcar uma escala em um termômetro, precisamos de um conjunto de valores de referência: Duas das mais usadas são as temperaturas de congelamento e ebulição da água a uma pressão atmosférica especificada. Na escala Celsius, 0 °C é definido como a temperatura de congelamento da água e 100 °C como a temperatura de ebulição da água. O espaço entre as duas temperaturas é dividido em 100 intervalos iguais, que chamamos de graus. Na escala Fahrenheit, o ponto de congelamento da água é definido como 32° F e a temperatura de ebulição como 212° F. O espaço entre esses dois pontos em um termômetro Fahrenheit é dividido em 180 partes iguais (graus).
Definir as escalas de temperatura em Celsius e Fahrenheit conforme descrito no parágrafo anterior resulta em uma relação um pouco mais complexa entre os valores de temperatura nessas duas escalas do que para unidades de medida diferentes para outras propriedades. A maioria das unidades de medida de uma determinada propriedade é diretamente proporcional uma à outra (y = mx). Usando unidades de comprimento conhecidas como um exemplo:
\[\mathrm{length\: in\: feet=\left(\dfrac{1\: ft}{12\: in.}\right)\times length\: in\: inches} \nonumber \]
onde
- y = comprimento em pés,
- x = comprimento em polegadas e
- a constante de proporcionalidade, m, é o fator de conversão.
As escalas de temperatura Celsius e Fahrenheit, no entanto, não compartilham um ponto zero comum e, portanto, a relação entre essas duas escalas é linear e não proporcional (\(y = mx + b\)). Consequentemente, converter uma temperatura de uma dessas escalas em outra requer mais do que uma simples multiplicação por um fator de conversão, m, mas também deve levar em consideração as diferenças nos pontos zero da escala (\(b\)).
A equação linear que relaciona as temperaturas Celsius e Fahrenheit é facilmente derivada das duas temperaturas usadas para definir cada escala. Representando a temperatura Celsius como\(x\) e a temperatura em Fahrenheit como\(y\), a inclinação\(m\),, é calculada para ser:
\[\begin{align*} m &=\dfrac{\Delta y}{\Delta x} \\[4pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\end{align*} \nonumber \]
O intercepto y da equação, b, é então calculado usando um dos pares de temperatura equivalentes, (100 °C, 212 °F) ou (0 °C, 32 °F), como:
\[\begin{align*} b&=y-mx \\[4pt] &= \mathrm{32\:^\circ F-\dfrac{9\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[4pt] &= \mathrm{32\:^\circ F} \end{align*} \nonumber \]
A equação que relaciona as escalas de temperatura é então:
\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{9\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C} \nonumber \]
Uma forma abreviada dessa equação que omite as unidades de medida é:
\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{9}{5}\times \mathit{T}_{^\circ C}+32} \nonumber \]
O rearranjo dessa equação produz a forma útil para converter de Fahrenheit para Celsius:
\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{5}{9}(\mathit{T}_{^\circ F}+32)} \nonumber \]
Conforme mencionado anteriormente neste capítulo, a unidade de temperatura SI é o kelvin (K). Diferente das escalas Celsius e Fahrenheit, a escala kelvin é uma escala de temperatura absoluta na qual 0 (zero) K corresponde à temperatura mais baixa que teoricamente pode ser alcançada. A descoberta do início do século XIX da relação entre o volume e a temperatura de um gás sugeriu que o volume de um gás seria zero a −273,15 °C. Em 1848, o físico britânico William Thompson, que mais tarde adotou o título de Lord Kelvin, propôs uma escala absoluta de temperatura baseada nesse conceito (mais o tratamento deste tópico é fornecido no capítulo deste texto sobre gases).
A temperatura de congelamento da água nesta escala é 273,15 K e sua temperatura de ebulição 373,15 K. Observe que a diferença numérica nessas duas temperaturas de referência é 100, a mesma da escala Celsius, e assim a relação linear entre essas duas escalas de temperatura exibirá uma inclinação de\(\mathrm{1\:\dfrac{K}{^\circ\:C}}\). Seguindo a mesma abordagem, as equações para conversão entre as escalas de temperatura de Kelvin e Celsius são derivadas como sendo:
\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15 \nonumber \]
\[T_\mathrm{^\circ C}=T_{\ce K}-273.15 \nonumber \]
O 273,15 nessas equações foi determinado experimentalmente, então não é exato. A figura\(\PageIndex{1}\) mostra a relação entre as três escalas de temperatura. Lembre-se de que não usamos o sinal de grau com temperaturas na escala Kelvin.
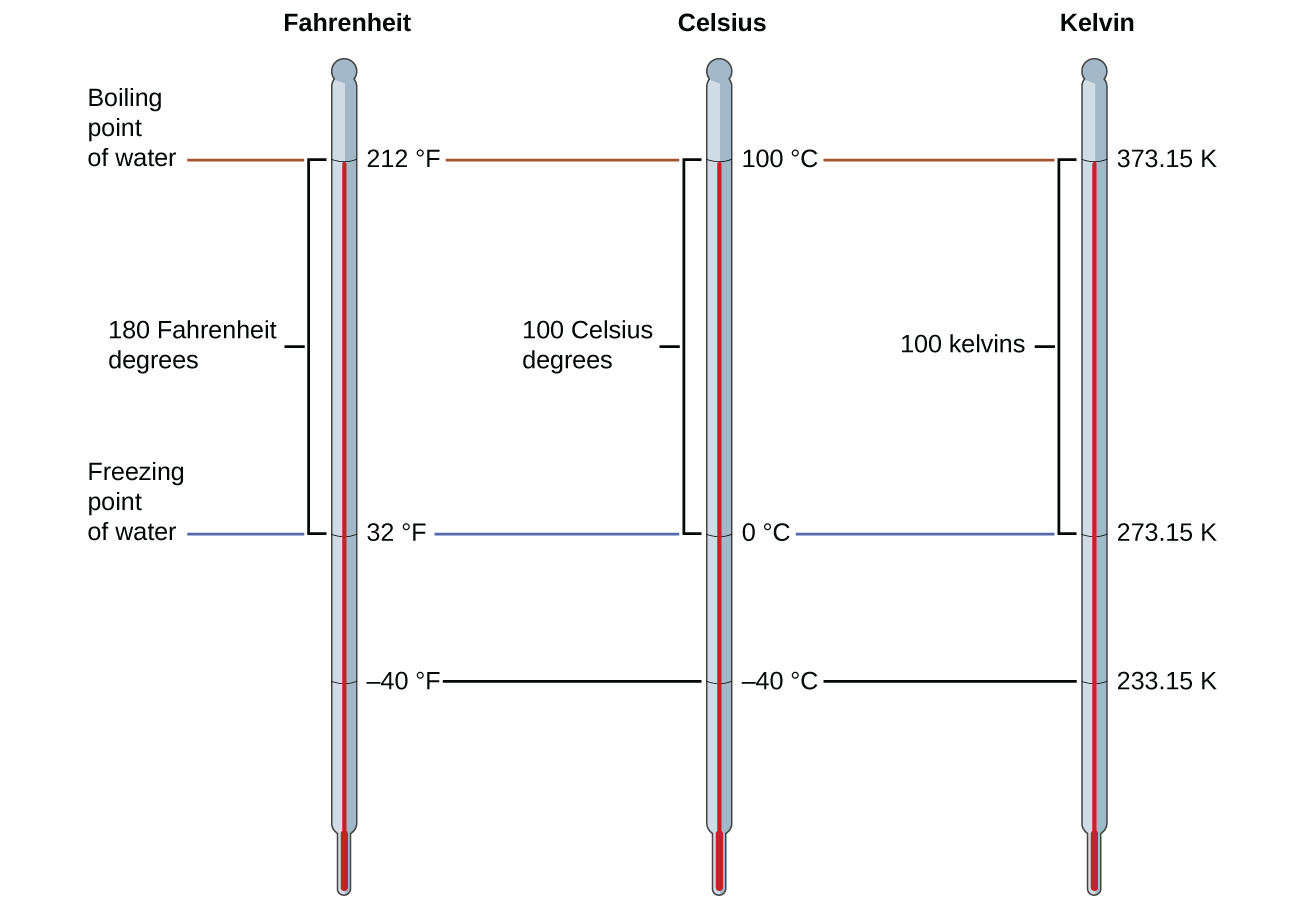
Embora a escala de temperatura Kelvin (absoluta) seja a escala oficial de temperatura SI, Celsius é comumente usada em muitos contextos científicos e é a escala de escolha para contextos não científicos em quase todas as áreas do mundo. Muito poucos países (EUA e seus territórios, Bahamas, Belize, Ilhas Cayman e Palau) ainda usam Fahrenheit para clima, remédios e culinária.
A temperatura corporal normal tem sido comumente aceita como 37,0° C (embora varie dependendo da hora do dia e do método de medição, bem como entre os indivíduos). Qual é essa temperatura na escala Kelvin e na escala Fahrenheit?
Solução
\[\mathrm{K= {^\circ C}+273.15=37.0+273.2=310.2\: K}\nonumber \]
\[\mathrm{^\circ F=\dfrac{9}{5}\:{^\circ C}+32.0=\left(\dfrac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F}\nonumber \]
Converta 80,92 °C em K e °F.
- Resposta
-
354.07 KM, 177.7 °F
Assar uma pizza pronta exige uma temperatura de forno de 450° F. Se você estiver na Europa e o termômetro do forno usa a escala Celsius, qual é a configuração? Qual é a temperatura do Kelvin?
Solução
\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{5}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)}\nonumber \]
\[\mathrm{K={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^2\,K\hspace{20px}(two\: significant\: figures)}\nonumber \]
Converta 50 °F em °C e K.
- Resposta
-
100 °C, 280 KG
Resumo
As medições são feitas usando uma variedade de unidades. Muitas vezes, é útil ou necessário converter uma quantidade medida de uma unidade em outra. Essas conversões são realizadas usando fatores de conversão de unidades, que são derivados de aplicações simples de uma abordagem matemática chamada método de rótulo fatorial ou análise dimensional. Essa estratégia também é empregada para calcular as quantidades buscadas usando quantidades medidas e relações matemáticas apropriadas.
Equações-chave
- \(T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32\)
- \(T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32\)
- \(T_\ce{K}={^\circ \ce C}+273.15\)
- \(T_\mathrm{^\circ C}=\ce K-273.15\)
Glossário
- análise dimensional
- (também, método de rótulo de fator) abordagem matemática versátil que pode ser aplicada a cálculos que variam de simples conversões de unidades a cálculos mais complexos e de várias etapas envolvendo várias quantidades diferentes
- Fahrenheit
- unidade de temperatura; a água congela a 32° F e ferve a 212° F nesta escala
- fator de conversão da unidade
- proporção de quantidades equivalentes expressas com unidades diferentes; usado para converter de uma unidade para uma unidade diferente


