7.3: Resolução de problemas
- Page ID
- 185849
As pessoas enfrentam problemas todos os dias — geralmente, vários problemas ao longo do dia. Às vezes, esses problemas são simples: para dobrar uma receita de massa de pizza, por exemplo, basta dobrar cada ingrediente da receita. Às vezes, porém, os problemas que encontramos são mais complexos. Por exemplo, digamos que você tenha um prazo de trabalho e deva enviar uma cópia impressa de um relatório ao seu supervisor até o final do dia útil. O relatório é urgente e deve ser enviado da noite para o dia. Você terminou o relatório ontem à noite, mas sua impressora não funcionará hoje. O que você deve fazer? Primeiro, você precisa identificar o problema e depois aplicar uma estratégia para solucioná-lo.
Estratégias de resolução de problemas
Quando você se depara com um problema — seja ele um problema matemático complexo ou uma impressora quebrada, como resolvê-lo? Antes de encontrar uma solução para o problema, o problema deve primeiro ser claramente identificado. Depois disso, uma das muitas estratégias de resolução de problemas pode ser aplicada, esperançosamente resultando em uma solução.
Uma estratégia de resolução de problemas é um plano de ação usado para encontrar uma solução. Estratégias diferentes têm diferentes planos de ação associados a elas (Tabela 7.2). Por exemplo, uma estratégia bem conhecida é a tentativa e erro. O velho ditado, “Se no início você não tiver sucesso, tente, tente novamente” descreve tentativa e erro. Em termos de sua impressora quebrada, você pode tentar verificar os níveis de tinta e, se isso não funcionar, verifique se a bandeja de papel não está atolada. Ou talvez a impressora não esteja realmente conectada ao seu laptop. Ao usar tentativa e erro, você continuaria tentando soluções diferentes até resolver o problema. Embora a tentativa e erro normalmente não seja uma das estratégias mais eficientes em termos de tempo, ela é comumente usada.
| Estratégias de resolução de problemas | ||
|---|---|---|
| Método | Descrição | Exemplo |
| Tentativa e erro | Continue tentando soluções diferentes até que o problema seja resolvido | Reiniciando o telefone, desligando o WiFi, desligando o bluetooth para determinar por que o telefone está com defeito |
| algoritmo | Fórmula de resolução de problemas passo a passo | Manual de instruções para instalar um novo software em seu computador |
| Heurística | Estrutura geral de resolução de problemas | Trabalhando de trás para frente; dividindo uma tarefa em etapas |
Outro tipo de estratégia é um algoritmo. Um algoritmo é uma fórmula de resolução de problemas que fornece instruções passo a passo usadas para alcançar o resultado desejado (Kahneman, 2011). Você pode pensar em um algoritmo como uma receita com instruções altamente detalhadas que produzem o mesmo resultado toda vez que são executadas. Algoritmos são usados com frequência em nossa vida cotidiana, especialmente na ciência da computação. Quando você faz uma pesquisa na Internet, mecanismos de busca como o Google usam algoritmos para decidir quais entradas aparecerão primeiro na sua lista de resultados. O Facebook também usa algoritmos para decidir quais postagens exibir em seu feed de notícias. Você consegue identificar outras situações nas quais os algoritmos são usados?
Uma heurística é outro tipo de estratégia de resolução de problemas. Embora um algoritmo deva ser seguido exatamente para produzir um resultado correto, uma heurística é uma estrutura geral de resolução de problemas (Tversky & Kahneman, 1974). Você pode pensar neles como atalhos mentais usados para resolver problemas. Uma “regra prática” é um exemplo de heurística. Essa regra economiza tempo e energia para a pessoa ao tomar uma decisão, mas apesar de suas características que economizam tempo, nem sempre é o melhor método para tomar uma decisão racional. Diferentes tipos de heurística são usados em diferentes tipos de situações, mas o impulso de usar uma heurística ocorre quando uma das cinco condições é atendida (Pratkanis, 1989):
Trabalhar de trás para frente é uma heurística útil na qual você começa a resolver o problema focando no resultado final. Considere este exemplo: você mora em Washington, D.C. e foi convidado para um casamento às 16h no sábado na Filadélfia. Sabendo que a Interestadual 95 tende a funcionar em qualquer dia da semana, você precisa planejar sua rota e programar sua partida de acordo. Se você quiser estar no serviço de casamento às 15h30 e levar 2,5 horas para chegar à Filadélfia sem trânsito, a que horas você deve sair de casa? Você usa a heurística inversa para planejar os eventos do seu dia regularmente, provavelmente sem sequer pensar nisso.
Outra heurística útil é a prática de realizar uma grande meta ou tarefa dividindo-a em uma série de etapas menores. Os alunos costumam usar esse método comum para concluir um grande projeto de pesquisa ou um longo ensaio para a escola. Por exemplo, os alunos geralmente discutem, desenvolvem uma tese ou tópico principal, pesquisam o tópico escolhido, organizam suas informações em um esboço, escrevem um rascunho, revisam e editam o rascunho, desenvolvem um rascunho final, organizam a lista de referências e revisam seu trabalho antes de entregar o projeto. A tarefa grande se torna menos trabalhosa quando é dividida em uma série de pequenas etapas.
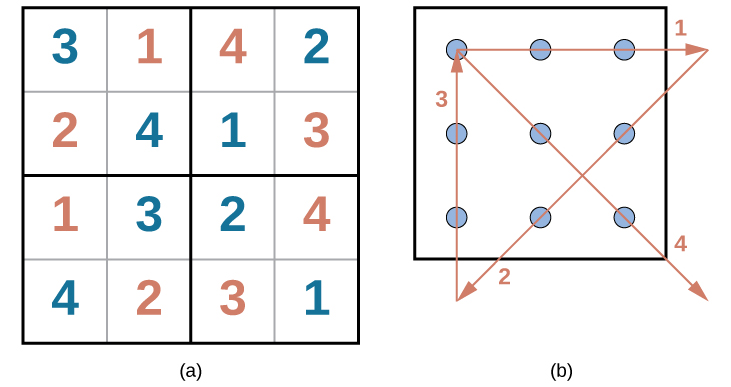
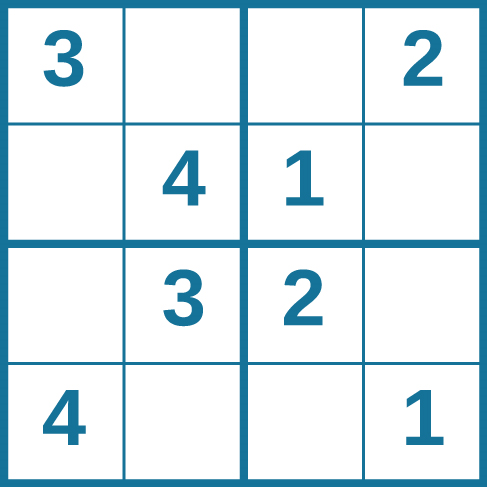
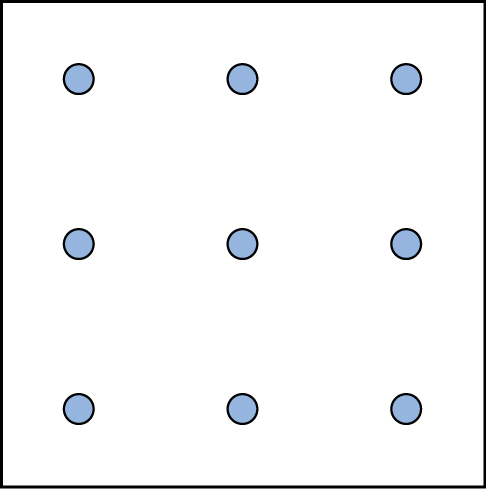
As habilidades de resolução de problemas podem melhorar com a prática. Muitas pessoas se desafiam todos os dias com quebra-cabeças e outros exercícios mentais para aprimorar suas habilidades de resolução de problemas. Os quebra-cabeças de Sudoku aparecem diariamente na maioria dos jornais. Normalmente, um quebra-cabeça sudoku é uma grade 9 × 9. O sudoku simples abaixo (Figura 7.7) é uma grade 4 × 4. Para resolver o quebra-cabeça, preencha as caixas vazias com um único dígito: 1, 2, 3 ou 4. Aqui estão as regras: Os números devem totalizar 10 em cada caixa em negrito, cada linha e cada coluna; no entanto, cada dígito só pode aparecer uma vez em uma caixa, linha e coluna em negrito. Avalie seu tempo ao resolver esse quebra-cabeça e compare seu tempo com o de um colega de classe.
Armadilhas para a solução de problemas
No entanto, nem todos os problemas são resolvidos com sucesso. Quais desafios nos impedem de resolver um problema com sucesso? Albert Einstein disse uma vez: “Insanidade é fazer a mesma coisa repetidamente e esperar um resultado diferente”. Imagine uma pessoa em uma sala com quatro portas. Uma porta que sempre esteve aberta no passado agora está trancada. A pessoa, acostumada a sair da sala por aquela porta em particular, continua tentando sair pela mesma porta, mesmo que as outras três portas estejam abertas. A pessoa está presa, mas ela só precisa ir até outra porta, em vez de tentar sair pela porta trancada. Um conjunto mental é quando você persiste em abordar um problema de uma forma que funcionou no passado, mas claramente não está funcionando agora.
A fixação funcional é um tipo de conjunto mental em que você não consegue perceber um objeto sendo usado para algo diferente do que foi projetado. Duncker (1945) conduziu uma pesquisa fundamental sobre a fixação funcional. Ele criou um experimento no qual os participantes receberam uma vela, um livro de fósforos e uma caixa de tachinhas. Eles foram instruídos a usar esses itens para prender a vela na parede para que ela não pingasse cera na mesa abaixo. Os participantes tiveram que usar a fixação funcional para resolver o problema (Figura 7.10). Durante a missão da Apollo 13 à Lua, os engenheiros da NASA no Mission Control tiveram que superar a fixação funcional para salvar a vida dos astronautas a bordo da espaçonave. Uma explosão em um módulo da espaçonave danificou vários sistemas. Os astronautas corriam o risco de serem envenenados pelo aumento dos níveis de dióxido de carbono devido a problemas com os filtros de dióxido de carbono. Os engenheiros descobriram uma maneira de os astronautas usarem sacos plásticos, fitas adesivas e mangueiras de ar sobressalentes para criar um filtro de ar improvisado, que salvou a vida dos astronautas.
Pesquisadores investigaram se a fixação funcional é afetada pela cultura. Em um experimento, indivíduos do grupo Shuar, no Equador, foram convidados a usar um objeto para uma finalidade diferente daquela para a qual o objeto foi originalmente planejado. Por exemplo, os participantes receberam uma história sobre um urso e um coelho separados por um rio e foram convidados a selecionar entre vários objetos, incluindo uma colher, um copo, borrachas e assim por diante, para ajudar os animais. A colher era o único objeto longo o suficiente para atravessar o rio imaginário, mas se a colher fosse apresentada de uma forma que refletisse seu uso normal, os participantes demoraram mais para escolher a colher para resolver o problema. (German & Barrett, 2005). Os pesquisadores queriam saber se a exposição a ferramentas altamente especializadas, como ocorre com indivíduos em países industrializados, afeta sua capacidade de transcender a fixação funcional. Foi determinado que a fixação funcional é experimentada em culturas industrializadas e não industrializadas (German & Barrett, 2005).
Para tomar boas decisões, usamos nosso conhecimento e nosso raciocínio. Muitas vezes, esse conhecimento e raciocínio são sólidos e sólidos. Às vezes, no entanto, somos influenciados por preconceitos ou por outras pessoas manipulando uma situação. Por exemplo, digamos que você e três amigos quisessem alugar uma casa e tivessem um orçamento alvo combinado de $1.600. O corretor de imóveis mostra apenas casas muito degradadas por $1.600 e depois mostra uma casa muito bonita por $2.000. Você pode pedir a cada pessoa que pague mais em aluguel para conseguir a casa de $2.000? Por que o corretor de imóveis lhe mostraria as casas degradadas e a bela casa? O corretor de imóveis pode estar desafiando seu viés de ancoragem. Um viés de ancoragem ocorre quando você se concentra em uma informação ao tomar uma decisão ou resolver um problema. Nesse caso, você está tão focado na quantidade de dinheiro que está disposto a gastar que pode não reconhecer quais tipos de casas estão disponíveis nessa faixa de preço.
O viés de confirmação é a tendência de se concentrar em informações que confirmam suas crenças existentes. Por exemplo, se você acha que seu professor não é muito legal, você percebe todos os casos de comportamento rude exibidos pelo professor, ignorando as inúmeras interações agradáveis em que ele se envolve diariamente. O preconceito retrospectivo leva você a acreditar que o evento que você acabou de vivenciar era previsível, mesmo que na verdade não fosse. Em outras palavras, você sempre soube que as coisas aconteceriam do jeito que aconteceram. O preconceito representativo descreve uma maneira errada de pensar, na qual você, sem querer, estereotipa alguém ou algo; por exemplo, você pode presumir que seus professores passam o tempo livre lendo livros e conversando intelectualmente, porque a ideia de eles passarem o tempo brincando voleibol ou visitar um parque de diversões não se encaixam em seus estereótipos de professores.
Finalmente, a heurística de disponibilidade é uma heurística na qual você toma uma decisão com base em um exemplo, informação ou experiência recente que está prontamente disponível para você, mesmo que possa não ser o melhor exemplo para informar sua decisão. Os preconceitos tendem a “preservar o que já está estabelecido — para manter nosso conhecimento, crenças, atitudes e hipóteses preexistentes” (Aronson, 1995; Kahneman, 2011). Esses vieses estão resumidos na Tabela 7.3.
| Resumo dos vieses de decisão | |
|---|---|
| Viés | Descrição |
| Ancoragem | Tendência de se concentrar em uma informação específica ao tomar decisões ou resolver problemas |
| Confirmação | Concentra-se em informações que confirmam as crenças existentes |
| Retrospectiva | A crença de que o evento que acabamos de experimentar era previsível |
| Representante | Estereótipos não intencionais de alguém ou algo |
| Disponibilidade | A decisão é baseada em um precedente disponível ou em um exemplo que pode estar incorreto |
Assista a este videoclipe feito por professores sobre preconceitos cognitivos para saber mais.