6.2: Gráficos das outras funções trigonométricas
- Page ID
- 189175
- Analise o gráfico de\(y=\tan x\).
- Variações gráficas de\(y=\tan x\).
- Analise os gráficos de\(y=\sec x\)\(y=\csc x\) e.
- Variações gráficas de\(y=\sec x\)\(y=\csc x\) e.
- Analise o gráfico de\(y=\cot x\).
- Variações gráficas de\(y=\cot x\).
Sabemos que a função tangente pode ser usada para encontrar distâncias, como a altura de um edifício, montanha ou mastro de bandeira. Mas e se quisermos medir ocorrências repetidas de distância? Imagine, por exemplo, um carro da polícia estacionado ao lado de um armazém. A luz giratória do carro da polícia atravessava a parede do armazém em intervalos regulares. Se a entrada for tempo, a saída seria a distância percorrida pelo feixe de luz. O feixe de luz repetiria a distância em intervalos regulares. A função tangente pode ser usada para aproximar essa distância. Seriam necessárias assíntotas para ilustrar os ciclos repetidos quando o feixe corre paralelo à parede porque, aparentemente, o feixe de luz pode parecer se estender para sempre. O gráfico da função tangente ilustraria claramente os intervalos repetidos. Nesta seção, exploraremos os gráficos da tangente e outras funções trigonométricas.
Analisando o gráfico de\(y =\tan x\)
Começaremos com o gráfico da função tangente, traçando pontos como fizemos para as funções seno e cosseno. Lembre-se de que
\[\tan \, x=\dfrac{\sin \, x}{\cos \, x}\]
O período da função tangente ocorre\(\pi\) porque o gráfico se repete em intervalos de\(k\pi\) onde\(k\) é uma constante. Se representarmos graficamente a função tangente em\(−\frac{\pi}{2}\) até\(\frac{\pi}{2}\), podemos ver o comportamento do gráfico em um ciclo completo. Se observarmos qualquer intervalo maior, veremos que as características do gráfico se repetem.
Podemos determinar se a tangente é uma função ímpar ou par usando a definição de tangente.
\[\begin{align*} \tan(-x)&= \dfrac{\sin(-x)}{\cos(-x)} \qquad \text{Definition of tangent}\\ &= \dfrac{-\sin \, x}{\cos \, x} \qquad \text{Sine is an odd function, cosine is even}\\ &= -\dfrac{\sin \, x}{\cos \, x} \qquad \text{The quotient of an odd and an even function is odd}\\ &= -\tan \, x \qquad \text{Definition of tangent} \end{align*}\]
Portanto, a tangente é uma função ímpar. Podemos analisar ainda mais o comportamento gráfico da função tangente observando os valores de alguns dos ângulos especiais, conforme listado na Tabela\(\PageIndex{1}\).
| \(x\) | \(−\dfrac{\pi}{2}\) | \(−\dfrac{\pi}{3}\) | \(−\dfrac{\pi}{4}\) | \(−\dfrac{\pi}{6}\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\tan x\) | indefinida | \(-\sqrt{3}\) | \(–1\) | \(-\dfrac{\sqrt{3}}{3}\) | 0 | \(\dfrac{\sqrt{3}}{3}\) | 1 | \(\sqrt{3}\) | indefinida |
Esses pontos nos ajudarão a desenhar nosso gráfico, mas precisamos determinar como o gráfico se comporta onde não está definido. Se olharmos mais de perto os valores quando\(\frac{\pi}{3}<x<\frac{\pi}{2}\), podemos usar uma tabela para procurar uma tendência. Porque\(\frac{\pi}{3}≈1.05\) e\(\frac{\pi}{2}≈1.57\), avaliaremos em medidas\(x\) em radianos\(1.05<x<1.57\), conforme mostrado na Tabela\(\PageIndex{2}\).
| \(x\) | 1.3 | 1,5 | 1,55 | 1,56 |
|---|---|---|---|---|
| \(\tan x\) | 3.6 | 14.1 | 48,1 | 92,6 |
Conforme\(x\) se aproxima\(\dfrac{\pi}{2}\), as saídas da função ficam cada vez maiores. Por ser\(y=\tan \, x\) uma função ímpar, vemos a tabela correspondente de valores negativos na Tabela\(\PageIndex{3}\).
| \(x\) | −1,3 | −1,5 | −1,5 | −1,56 |
|---|---|---|---|---|
| \(\tan x\) | −3,6 | −14,1 | −48,1 | −92,6 |
Podemos ver que, à medida que\(x\) se aproxima\(−\frac{\pi}{2}\), as saídas ficam cada vez menores. Lembre-se de que existem alguns valores de\(x\) para os quais\(\cos \, x=0\). Por exemplo,\(\cos \left (\frac{\pi}{2} \right)=0\)\(\cos \left (\frac{3\pi}{2} \right )=0\) e. Nesses valores, a função tangente é indefinida, então o gráfico de\(y=\tan \, x\) tem descontinuidades em\(x=\frac{\pi}{2}\)\(\frac{3\pi}{2}\) e. Nesses valores, o gráfico da tangente tem assíntotas verticais. \(\PageIndex{1}\)A figura representa o gráfico de\(y=\tan \, x\). A tangente é positiva de\(0\) para\(\frac{\pi}{2}\) e de\(\pi\) para\(\frac{3\pi}{2}\), correspondendo aos quadrantes I e III do círculo unitário.
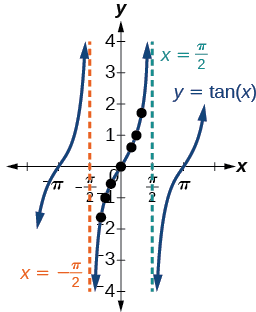
Figura\(\PageIndex{1}\): Gráfico da função tangente
Representação gráfica de variações de\(y = \tan \, x\)
Assim como acontece com as funções seno e cosseno, a função tangente pode ser descrita por uma equação geral.
\[y=A\tan(Bx) \nonumber\]
Podemos identificar alongamentos e compressões horizontais e verticais usando valores de\(A\)\(B\) e. O alongamento horizontal normalmente pode ser determinado a partir do período do gráfico. Com gráficos tangentes, muitas vezes é necessário determinar um alongamento vertical usando um ponto no gráfico.
Como não há valores máximos ou mínimos de uma função tangente, o termo amplitude não pode ser interpretado como é para as funções seno e cosseno. Em vez disso, usaremos a frase fator de alongamento/compressão ao nos referirmos à constante\(A\).
- O fator de alongamento é\(|A|\).
- O período é\(P=\dfrac{\pi}{|B|}\).
- O domínio é todo números reais\(x\), onde\(x≠\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) isso\(k\) é um número inteiro.
- O alcance é\((−\infty,\infty)\).
- As assíntotas ocorrem\(x=\dfrac{\pi}{2| B |}+\dfrac{π}{| B |}k\) onde\(k\) está um número inteiro.
- \(y=A\tan(Bx)\)é uma função estranha.
Representação gráfica de um período de uma função tangente esticada ou comprimida
Podemos usar o que sabemos sobre as propriedades da função tangente para esboçar rapidamente um gráfico de qualquer função tangente esticada e/ou comprimida da forma\(f(x)=A\tan(Bx)\). Nós nos concentramos em um único período da função, incluindo a origem, porque a propriedade periódica nos permite estender o gráfico para o resto do domínio da função, se quisermos. Nosso domínio limitado é então o intervalo\(\left (−\dfrac{P}{2},\dfrac{P}{2} \right )\) e o gráfico tem assíntotas verticais em\(\pm \dfrac{P}{2}\) onde\(P=\dfrac{\pi}{B}\). Em\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2} \right )\) seguida, o gráfico surgirá da assíntota esquerda em\(x=−\dfrac{\pi}{2}\), cruzará a origem e continuará a aumentar à medida que se aproxima da assíntota direita em\(x=\dfrac{\pi}{2}\). Para fazer com que a função se aproxime das assíntotas na taxa correta, também precisamos definir a escala vertical avaliando a função para pelo menos um ponto pelo qual o gráfico passará. Por exemplo, podemos usar
\[f \left (\dfrac{P}{4} \right )=A\tan \left (B\dfrac{P}{4} \right )=A\tan \left (B\dfrac{\pi}{4B} \right )=A \nonumber\]
porque\(\tan \left (\dfrac{\pi}{4} \right )=1\).
- Identifique o fator de alongamento,\(| A |\).
- Identifique B e determine o período,\(P=\dfrac{\pi}{| B |}\).
- Desenhe assíntotas verticais em\(x=−\dfrac{P}{2}\)\(x=\dfrac{P}{2}\) e.
- \(A>0\)Pois, o gráfico se aproxima da assíntota esquerda em valores de saída negativos e da assíntota direita em valores de saída positivos (inverso para\(A<0\)).
- Faça um gráfico dos pontos de referência em\(\left (\dfrac{P}{4},A \right )\)\((0,0)\),\(\left (−\dfrac{P}{4},−A \right )\), e e desenhe o gráfico através desses pontos.
Esboce um gráfico de um período da função\(y=0.5\tan \left (\dfrac{\pi}{2}x \right )\).
Solução
Primeiro, identificamos\(A\)\(B\) e.
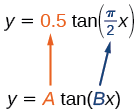
Figura\(\PageIndex{2}\)
Porque\(A=0.5\) e\(B=\dfrac{\pi}{2}\), podemos encontrar o fator e o período de alongamento/compressão. O período é\(\dfrac{\pi}{\dfrac{\pi}{2}}=2\), então as assíntotas estão em\(x=±1\). Em um período de um quarto da origem, temos
\[\begin{align*} f(0.5)&= 0.5\tan \left (\dfrac{0.5\pi}{2} \right )\\ &= 0.5\tan \left (\dfrac{\pi}{4} \right )\\ &= 0.5 \end{align*}\]
Isso significa que a curva deve passar pelos pontos\((0.5,0.5)\)\((0,0)\),\((−0.5,−0.5)\) e. O único ponto de inflexão está na origem. A figura\(\PageIndex{3}\) mostra o gráfico de um período da função.
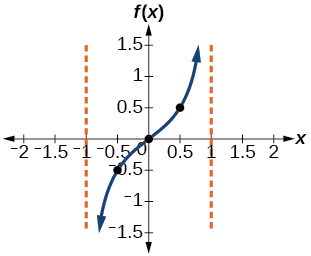
Figura\(\PageIndex{3}\)
Esboce um gráfico de\(f(x)=3\tan \left (\dfrac{\pi}{6}x \right )\).
- Responda
-

Figura\(\PageIndex{4}\)
Representação gráfica de um período de uma função tangente deslocada
Agora que podemos representar graficamente uma função tangente que está esticada ou comprimida, adicionaremos uma mudança vertical e/ou horizontal (ou de fase). Nesse caso, adicionamos\(C\) e\(D\) à forma geral da função tangente.
\[f(x)=A\tan(Bx−C)+D \nonumber\]
O gráfico de uma função tangente transformada é diferente da função tangente básica\(\tan x\) de várias maneiras:
- O fator de alongamento é\(| A |\).
- O período é\(\dfrac{\pi}{| B |}\).
- O domínio é\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) é um número inteiro.
- O alcance é\((−∞,−| A |]∪[| A |,∞)\).
- As assíntotas verticais ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) há um número inteiro ímpar.
- Não há amplitude.
- \(y=A \tan(Bx)\)é uma função ímpar porque é o quociente de funções pares e ímpares (seno e cosseno, em perspectiva).
- Expresse a função dada no formulário\(y=A\tan(Bx−C)+D\).
- Identifique o fator de alongamento/compressão,\(| A |\).
- Identifique\(B\) e determine o período,\(P=\dfrac{\pi}{|B|}\).
- Identifique\(C\) e determine a mudança de fase,\(\dfrac{C}{B}\).
- Desenhe o gráfico de\(y=A\tan(Bx)\) deslocado para a direita em\(\dfrac{C}{B}\) e para cima em\(D\).
- Desenhe as assíntotas verticais, que ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), onde\(k\) há um número inteiro ímpar.
- Faça um gráfico de três pontos de referência e desenhe o gráfico através desses pontos.
Faça um gráfico de um período da função\(y=−2\tan(\pi x+\pi)−1\).
Solução
- Etapa 1. A função já está escrita no formulário\(y=A\tan(Bx−C)+D\).
- Etapa 2. \(A=−2\), então o fator de alongamento é\(|A|=2\).
- Etapa 3. \(B=\ pi\), então o período é\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{pi}=1\).
- Etapa 4. \(C=−\ pi\), então a mudança de fase é\(CB=\dfrac{−\pi}{\pi}=−1\).
- Etapa 5-7. As assíntotas estão em\(x=−\dfrac{3}{2}\)\(x=−\dfrac{1}{2}\) e e e os três pontos de referência recomendados são\((−1.25,1)\)\((−1,−1)\),\((−0.75,−3)\) e. O gráfico é mostrado na Figura\(\PageIndex{5}\).
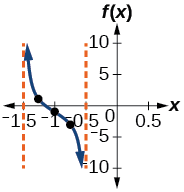
Figura\(\PageIndex{5}\)
Análise
Observe que essa é uma função decrescente porque\(A<0\).
Como o gráfico em\(\PageIndex{2}\) Example seria diferente se fizéssemos\(A=2\) em vez de\(−2\)?
- Responda
-
Isso se refletiria em toda a linha\(y=−1\), tornando-se uma função crescente.
- Encontre o período a\(P\) partir do espaçamento entre assíntotas verticais sucessivas ou interceptações x.
- Escreva\(f(x)=A\tan \left (\dfrac{\pi}{P}x \right )\).
- Determine um ponto conveniente\((x,f(x))\) no gráfico fornecido e use-o para determinar\(A\).
Encontre uma fórmula para a função representada graficamente na Figura\(\PageIndex{6}\).
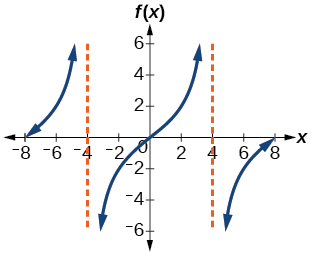
Figura\(\PageIndex{6}\): Uma função tangente esticada
Solução
O gráfico tem a forma de uma função tangente.
- Etapa 1. Um ciclo se estende de\(–4\) até\(4\), então o período é\(P=8\). Desde então\(P=\dfrac{\pi}{| B |}\), nós temos\(B=\dfrac{π}{P}=\dfrac{\pi}{8}\).
- Etapa 2. A equação deve ter a forma\(f(x)=A\tan \left (\dfrac{\pi}{8}x \right )\).
- Etapa 3. Para encontrar o trecho vertical\(A\), podemos usar o ponto\((2,2)\). \[\begin{align*} 2&=A\tan \left (\dfrac{\pi}{8}\cdot 2 \right )\\ &=A\tan \left (\dfrac{\pi}{4} \right ) \end{align*}\]
Porque\(\tan \left (\dfrac{\pi}{4} \right )=1\),\(A=2\).
Essa função teria uma fórmula\(f(x)=2\tan \left (\dfrac{\pi}{8}x \right )\).
Encontre uma fórmula para a função na Figura\(\PageIndex{7}\).
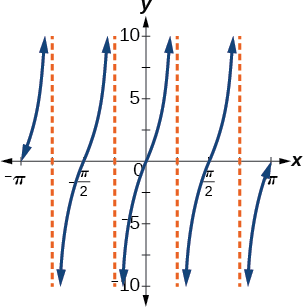
Figura\(\PageIndex{7}\)
- Responda
-
\(g(x)=4\tan(2x)\)
Analisando os gráficos de\(y = \sec x\) e\(y = \csc x\)
A secante foi definida pela identidade recíproca\(sec \, x=\dfrac{1}{\cos x}\). Observe que a função é indefinida quando o cosseno é\(0\), levando a assíntotas verticais em\(\dfrac{\pi}{2}\),\(\dfrac{3\pi}{2}\) etc. Como o cosseno nunca é maior do que\(1\) em valor absoluto, a secante, sendo a recíproca, nunca será menor do que\(1\) em valor absoluto.
Podemos representar graficamente\(y=\sec x\) observando o gráfico da função cosseno porque essas duas funções são recíprocas uma da outra. Veja a Figura\(\PageIndex{8}\). O gráfico do cosseno é mostrado como uma onda laranja tracejada para que possamos ver a relação. Onde o gráfico da função cosseno diminui, o gráfico da função secante aumenta. Onde o gráfico da função cosseno aumenta, o gráfico da função secante diminui. Quando a função cosseno é zero, a secante é indefinida.
O gráfico secante tem assíntotas verticais em cada valor de\(x\) onde o gráfico do cosseno cruza o\(x\) eixo -; nós as mostramos no gráfico abaixo com linhas verticais tracejadas, mas não mostraremos todas as assíntotas explicitamente em todos os gráficos posteriores envolvendo a secante e a cossecante.
Observe que, como o cosseno é uma função uniforme, a secante também é uma função uniforme. Isso é,\(\sec(−x)=\sec x\).
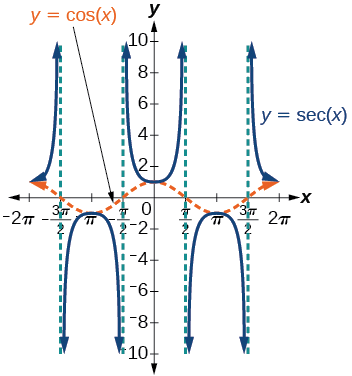
Figura\(\PageIndex{8}\): Gráfico da função secante,\(f(x)=\sec x=\dfrac{1}{\cos x}\)
Como fizemos com a função tangente, voltaremos a nos referir à constante\(| A |\) como o fator de alongamento, não a amplitude.
- O fator de alongamento é\(| A |\).
- O período é\(\dfrac{2\pi}{| B |}\).
- O domínio é\(x≠\dfrac{\pi}{2| B |}k\), onde\(k\) é um número inteiro ímpar.
- O alcance é\((−∞,−|A|]∪[|A|,∞)\).
- As assíntotas verticais ocorrem em\(x=\dfrac{\pi}{2| B |}k\), onde\(k\) há um número inteiro ímpar.
- Não há amplitude.
- \(y=A\sec(Bx)\)é uma função par porque o cosseno é uma função par.
Semelhante à secante, a cossecante é definida pela identidade recíproca\(\csc x=\dfrac{1}{\sin x}\). Observe que a função é indefinida quando o seno é\(0\), levando a uma assíntota vertical no gráfico em\(0\),\(\pi\), etc. Como o seno nunca é maior do que\(1\) em valor absoluto, a cossecante, sendo a recíproca, nunca será menor do que\(1\) em valor absoluto.
Podemos representar graficamente\(y=\csc x\) observando o gráfico da função seno porque essas duas funções são recíprocas uma da outra. Veja a Figura\(\PageIndex{7}\). O gráfico do seno é mostrado como uma onda laranja tracejada para que possamos ver a relação. Onde o gráfico da função senoidal diminui, o gráfico da função cossecante aumenta. Onde o gráfico da função senoidal aumenta, o gráfico da função cossecante diminui.
O gráfico cossecante tem assíntotas verticais em cada valor de\(x\) onde o gráfico senoidal cruza o\(x\) eixo -; nós as mostramos no gráfico abaixo com linhas verticais tracejadas.
Observe que, como o seno é uma função ímpar, a função cossecante também é uma função ímpar. Isso é,\(\csc(−x)=−\csc x\).
O gráfico da cossecante, mostrado na Figura\(\PageIndex{9}\), é semelhante ao gráfico da secante.
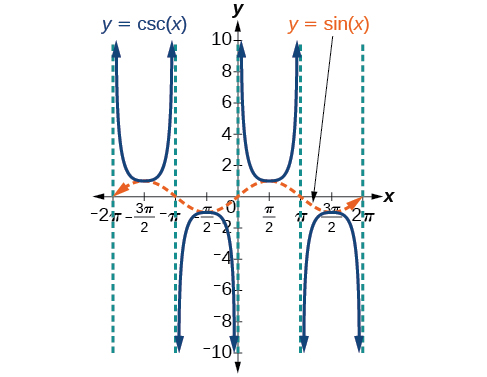
Figura\(\PageIndex{9}\): O gráfico da função cossecante,\(f(x)=\csc x=\frac{1}{\sin x}\)
- O fator de alongamento é\(| A |\).
- O período é\(\dfrac{2\pi}{|B|}\).
- O domínio é\(x≠\dfrac{\pi}{|B|}k\), onde\(k\) é um número inteiro.
- O alcance é\((−∞,−|A|]∪[|A|,∞)\).
- As assíntotas ocorrem em\(x=\dfrac{\pi}{| B |}k\), onde\(k\) é um número inteiro.
- \(y=A\csc(Bx)\)é uma função ímpar porque seno é uma função ímpar.
Representação gráfica de variações de\(y = \sec x\) e\(y= \csc x\)
Para versões deslocadas, comprimidas e/ou esticadas das funções secante e cossecante, podemos seguir métodos semelhantes aos que usamos para tangente e cotangente. Ou seja, localizamos as assíntotas verticais e também avaliamos as funções para alguns pontos (especificamente a extremidade local). Se quisermos representar graficamente apenas um único período, podemos escolher o intervalo para o período de mais de uma maneira. O procedimento para secante é muito semelhante, porque a identidade da cofunção significa que o gráfico secante é o mesmo que o gráfico cossecante deslocado meio período para a esquerda. Mudanças verticais e de fase podem ser aplicadas à função cossecante da mesma forma que para a secante e outras funções. As equações se tornam as seguintes.
\[y=A\sec(Bx−C)+D\]
\[y=A\csc(Bx−C)+D\]
- O fator de alongamento é\(|A|\).
- O período é\(\dfrac{2\pi}{|B|}\).
- O domínio é\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), onde\(k\) é um número inteiro ímpar.
- O alcance é\((−∞,−|A|]∪[|A|,∞)\).
- As assíntotas verticais ocorrem em\(x=\dfrac{C}{B}+\dfrac{π}{2| B |}k\), onde\(k\) há um número inteiro ímpar.
- Não há amplitude.
- \(y=A\sec(Bx)\)é uma função par porque o cosseno é uma função par.
- O fator de alongamento é\(|A|\).
- O período é\(\dfrac{2\pi}{|B|}\).
- O domínio é\(x≠\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), onde\(k\) é um número inteiro.
- O alcance é\((−∞,−|A|]∪[|A|,∞)\).
- As assíntotas verticais ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{|B|}k\), onde\(k\) é um número inteiro.
- Não há amplitude.
- \(y=A\csc(Bx)\)é uma função ímpar porque seno é uma função ímpar.
- Expresse a função dada no formulário\(y=A\sec(Bx)\).
- Identifique o fator de alongamento/compressão,\(|A|\).
- Identifique\(B\) e determine o período,\(P=\dfrac{2\pi}{| B |}\).
- Esboce o gráfico de\(y=A\cos(Bx)\).
- Use a relação recíproca entre\(y=\cos \, x\) e\(y=\sec \, x\) para desenhar o gráfico de\(y=A\sec(Bx)\).
- Esboce as assíntotas.
- Faça um gráfico de dois pontos de referência e desenhe o gráfico através desses pontos.
Faça um gráfico de um período de\(f(x)=2.5\sec(0.4x)\).
Solução
- Etapa 1. A função dada já está escrita na forma geral,\(y=A\sec(Bx)\).
- Etapa 2. \(A=2.5\)então o fator de alongamento é\(2.5\).
- Etapa 3. \(B=0.4\)então\(P=\dfrac{2\pi}{0.4}=5\pi\). O período é de\(5\pi\) unidades.
- Etapa 4. Esboce o gráfico da função\(g(x)=2.5\cos(0.4x)\).
- Etapa 5. Use a relação recíproca das funções cosseno e secante para desenhar a função cossecante.
- Etapas 6—7. Esboce duas assíntotas ao\(x=1.25\pi\) e ao\(x=3.75\pi\). Podemos usar dois pontos de referência, o mínimo local em\((0,2.5)\) e o máximo local em\((2.5\pi,−2.5)\). A figura\(\PageIndex{10}\) mostra o gráfico.
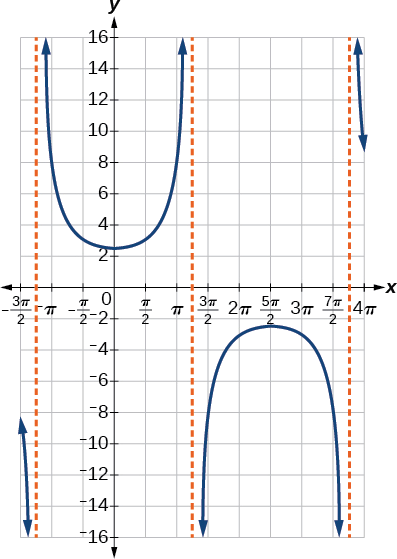
Figura\(\PageIndex{10}\)
Faça um gráfico de um período de\(f(x)=−2.5\sec(0.4x)\).
- Responda
-
Esse é um reflexo vertical do gráfico anterior porque\(A\) é negativo.
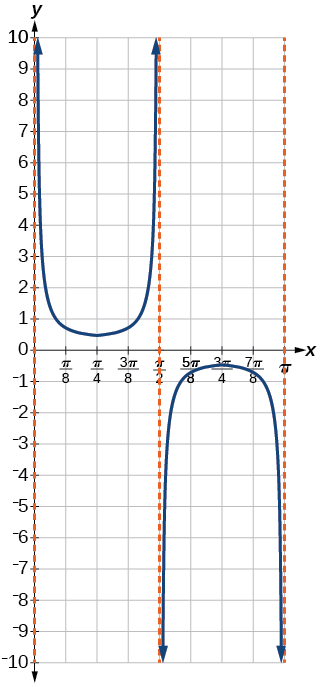
Figura\(\PageIndex{11}\)
Sim. O alcance de\(f(x)=A\sec(Bx−C)+D\) é\((−∞,−|A|+D]∪[|A|+D,∞)\).
- Expresse a função dada no formulário\(y=A \sec(Bx−C)+D\).
- Identifique o fator de alongamento/compressão,\(| A |\).
- Identifique\(B\) e determine o período,\(\dfrac{2\pi}{|B|}\).
- Identifique\(C\) e determine a mudança de fase,\(\dfrac{C}{B}\).
- Desenhe o gráfico de\(y=A \sec(Bx)\). mas desloque-o para a direita\(\dfrac{C}{B}\) e para cima\(D\).
- Desenhe as assíntotas verticais, que ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{2| B |}k\), onde\(k\) há um número inteiro ímpar.
Faça um gráfico de um período de\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
Solução
- Etapa 1. Expresse a função dada no formulário\(y=4\sec \left (\dfrac{\pi}{3x}−\dfrac{\pi}{2} \right )+1\).
- Etapa 2. O fator de alongamento/compressão é\(| A |=4\).
- Etapa 3. O período é
\[\begin{align*} \dfrac{2\pi}{|B|}&= \dfrac{2\pi}{\dfrac{\pi}{3}}\\ &= 2\pi \cdot \dfrac{3}{\pi}\\ &= 6 \end{align*}\]
- Etapa 4. A mudança de fase é
\[\begin{align*} \dfrac{C}{B}&= \dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{3}}\\ &= \dfrac{\pi}{2}\cdot \dfrac{3}{\pi}\\ &= 1.5 \end{align*}\]
- Etapa 5. Desenhe o gráfico de\(y=A\sec(Bx)\), mas desloque-o para a direita\(\dfrac{C}{B}=1.5\) e para cima em\(D=6\).
- Etapa 6. Esboce as assíntotas verticais\(x=0\), que ocorrem em\(x=3\),\(x=6\) e. Há um mínimo local em\((1.5,5)\) e um máximo local em\((4.5,−3)\). A figura\(\PageIndex{12}\) mostra o gráfico.
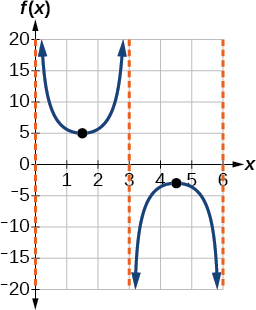
Figura\(\PageIndex{12}\)
Faça um gráfico de um período de\(f(x)=−6\sec(4x+2)−8\).
- Responda
-
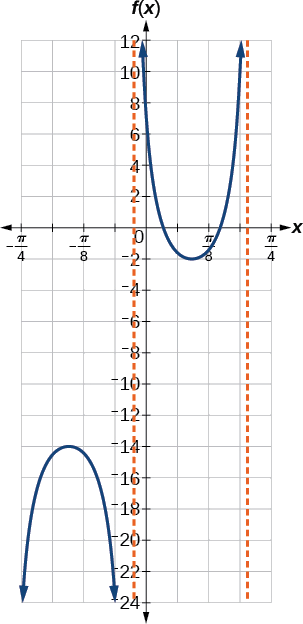
Figura\(\PageIndex{13}\)
Sim. Os pontos excluídos do domínio seguem as assíntotas verticais. Suas localizações mostram o deslocamento horizontal e a compressão ou expansão implícitas na transformação para a entrada da função original.
- Expresse a função dada no formulário\(y=A\csc(Bx)\).
- \(|A|\).
- Identifique\(B\) e determine o período,\(P=\dfrac{2\pi}{| B |}\).
- Desenhe o gráfico de\(y=A\sin(Bx)\).
- Use a relação recíproca entre\(y=sin \, x\) e\(y=\csc \, x\) para desenhar o gráfico de\(y=A\csc(Bx)\).
- Esboce as assíntotas.
- Faça um gráfico de dois pontos de referência e desenhe o gráfico através desses pontos.
Faça um gráfico de um período de\(f(x)=−3\csc(4x)\).
Solução
- Etapa 1. A função dada já está escrita na forma geral,\(y=A\csc(Bx)\).
- Etapa 2. \(| A |=| −3 |=3\), então o fator de alongamento é\(3\).
- Etapa 3. \(B=4\), então\(P=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\). O período é de\(\dfrac{\pi}{2}\) unidades.
- Etapa 4. Esboce o gráfico da função\(g(x)=−3\sin(4x)\).
- Etapa 5. Use a relação recíproca das funções seno e cossecante para desenhar a função cossecante.
- Etapas 6—7. Esboce três assíntotas em\(x=0\)\(x=\dfrac{\pi}{4}\),\(x=\dfrac{\pi}{2}\) e. Podemos usar dois pontos de referência, o máximo local em\(\left (\dfrac{\pi}{8},−3 \right )\) e o mínimo local em\(\left (\dfrac{3\pi}{8},3 \right )\). A figura\(\PageIndex{14}\) mostra o gráfico.
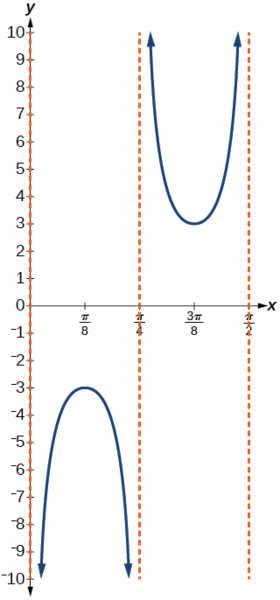
Figura\(\PageIndex{14}\)
Faça um gráfico de um período de\(f(x)=0.5\csc(2x)\).
- Responda
-
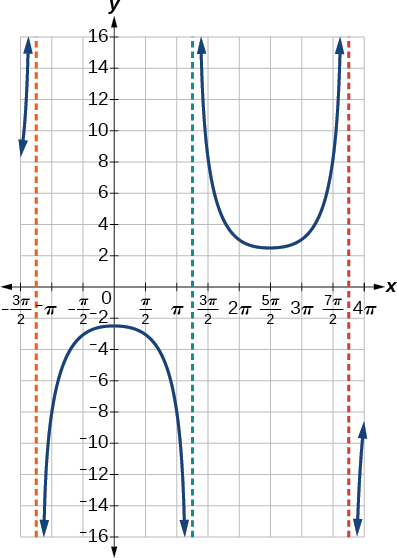
Figura\(\PageIndex{15}\)
- Expresse a função dada no formulário\(y=A\csc(Bx−C)+D\).
- Identifique o fator de alongamento/compressão,\(|A|\).
- Identifique\(B\) e determine o período,\(\dfrac{2\pi}{| B |}\).
- Identifique\(C\) e determine a mudança de fase,\(\dfrac{C}{B}\).
- Desenhe o gráfico de\(y=A\csc(Bx)\), mas desloque-o para a direita em e para cima\(D\).
- Desenhe as assíntotas verticais, que ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) está um número inteiro.
Esboce um gráfico de\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\). Quais são o domínio e o alcance dessa função?
Solução
- Etapa 1. Expresse a função dada no formulário\(y=2\csc \left (\dfrac{\pi}{2}x \right )+1\).
- Etapa 2. Identifique o fator de alongamento/compressão,\(| A |=2\).
- Etapa 3. O período é\(\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{\pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\).
- Etapa 4. A mudança de fase é\(\dfrac{0}{\dfrac{\pi}{2}}=0\).
- Etapa 5. Desenhe o gráfico\(y=A\csc(Bx)\), mas mude-o para cima\(D=1\).
- Etapa 6. Esboce as assíntotas verticais, que ocorrem em\(x=0\),\(x=2\),\(x=4\).
O gráfico dessa função é mostrado na Figura\(\PageIndex{16}\).
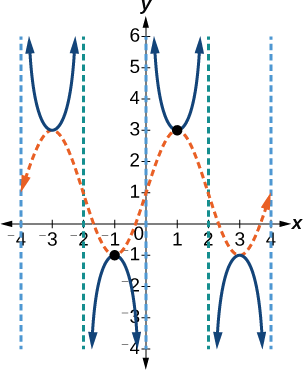
Figura\(\PageIndex{16}\): Uma função cossecante transformada
Análise
As assíntotas verticais mostradas no gráfico marcam um período da função, e a extremidade local nesse intervalo é mostrada por pontos. Observe como o gráfico da cossecante transformada se relaciona com o gráfico de\(f(x)=2\sin \left (\frac{\pi}{2}x \right )+1\), mostrado como a onda tracejada laranja.
Dado o gráfico\(f(x)=2\cos \left (\frac{\pi}{2}x \right )+1\) mostrado na Figura\(\PageIndex{17}\), esboce o gráfico de\(g(x)=2\sec \left (\dfrac{\pi}{2}x \right )+1\) nos mesmos eixos.
![Um gráfico de dois períodos de uma função coseno modificada. O intervalo é [-1,3], representado graficamente de x=-4 a x=4.](https://math.libretexts.org/@api/deki/files/14146/imageedit_56_4915587648.png)
Figura\(\PageIndex{17}\)
- Responda
-
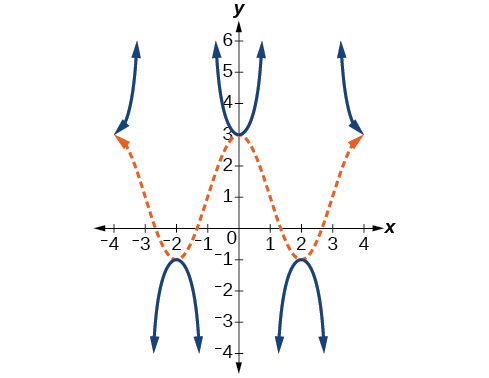
Figura\(\PageIndex{18}\)
Analisando o gráfico de\(y = \cot x\)
A última função trigonométrica que precisamos explorar é a cotangente. A cotangente é definida pela identidade recíproca\(cot \, x=\dfrac{1}{\tan x}\). Observe que a função é indefinida quando a função tangente é\(0\), levando a uma assíntota vertical no gráfico em\(0\)\(\pi\),, etc. Como a saída da função tangente é toda números reais, a saída da função cotangente também é toda números reais.
Podemos representar graficamente\(y=\cot x\) observando o gráfico da função tangente porque essas duas funções são recíprocas uma da outra. Veja a Figura\(\PageIndex{19}\). Onde o gráfico da função tangente diminui, o gráfico da função cotangente aumenta. Onde o gráfico da função tangente aumenta, o gráfico da função cotangente diminui.
O gráfico cotangente tem assíntotas verticais em cada valor de\(x\) onde\(\tan x=0\); nós as mostramos no gráfico abaixo com linhas tracejadas. Como a cotangente é a recíproca da tangente,\(\cot x\) tem assíntotas verticais em todos os valores de\(x\) onde\(\tan x=0\) e\(\cot x=0\) em todos os valores de\(x\) onde\(\tan x\) tem suas assíntotas verticais.
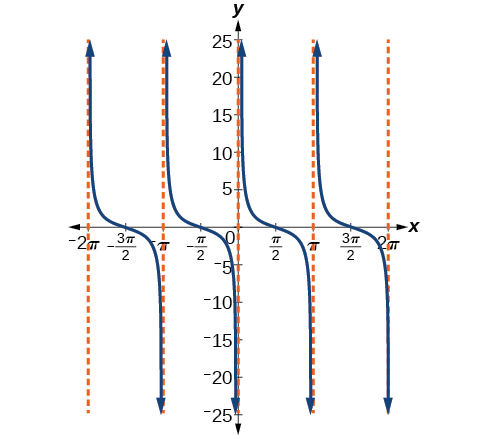
Figura\(\PageIndex{19}\): A função cotangente
- O fator de alongamento é\(|A|\).
- O período é\(P=\dfrac{\pi}{|B|}\).
- O domínio é\(x≠\dfrac{\pi}{|B|}k\), onde\(k\) é um número inteiro.
- O alcance é\((−∞,∞)\).
- As assíntotas ocorrem em\(x=\dfrac{\pi}{| B |}k\), onde\(k\) é um número inteiro.
- \(y=A\cot(Bx)\)é uma função estranha.
Representação gráfica de variações de\(y =\cot x\)
Podemos transformar o gráfico da cotangente da mesma forma que fizemos com a tangente. A equação se torna a seguinte.
\[y=A\cot(Bx−C)+D\]
- O fator de alongamento é\(| A |\).
- O período é\(\dfrac{\pi}{|B|}\)
- O domínio é\(x≠\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) é um número inteiro.
- O alcance é\((−∞,−|A|]∪[|A|,∞)\).
- As assíntotas verticais ocorrem em\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) é um número inteiro.
- Não há amplitude.
- \(y=A\cot(Bx)\)é uma função ímpar porque é o quociente de funções pares e ímpares (cosseno e seno, respectivamente)
- Expresse a função no formulário\(f(x)=A\cot(Bx)\).
- Identifique o fator de alongamento,\(|A|\).
- Identifique o período,\(P=\dfrac{\pi}{|B|}\).
- Desenhe o gráfico de\(y=A\tan(Bx)\).
- Faça um gráfico de quaisquer dois pontos de referência.
- Use a relação recíproca entre tangente e cotangente para desenhar o gráfico de\(y=Acot(Bx)\).
- Esboce as assíntotas.
Determine o fator de alongamento, o período e a mudança de fase de e\(y=3\cot(4x)\), em seguida, esboce um gráfico.
Solução
- Etapa 1. Expressar a função no formulário\(f(x)=A\cot(Bx)\) dá\(f(x)=3\cot(4x)\).
- Etapa 2. O fator de alongamento é\(|A|=3\).
- Etapa 3. O período é\(P=\dfrac{\pi}{4}\).
- Etapa 4. Esboce o gráfico de\(y=3\tan(4x)\).
- Etapa 5. Faça um gráfico de dois pontos de referência. Dois desses pontos são\(\left (\dfrac{\pi}{16},3 \right )\)\(\left (\dfrac{3\pi}{16},−3 \right )\) e.
- Etapa 6. Use a relação recíproca para desenhar\(y=3\cot(4x)\).
- Etapa 7. Esboce as assíntotas,\(x=0\),\(x=\dfrac{\pi}{4}\).
O gráfico laranja na Figura\(\PageIndex{20}\) mostra\(y=3\tan(4x)\) e o gráfico azul mostra\(y=3\cot(4x)\).
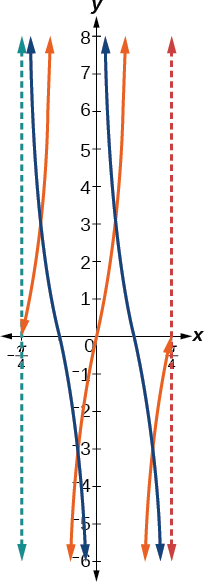
Figura\(\PageIndex{20}\)
- Expresse a função no formulário\(f(x)=A\cot(Bx−C)+D\).
- Identifique o fator de alongamento,\(| A |\).
- Identifique o período,\(P=\dfrac{\pi}{|B|}\).
- Identifique a mudança de fase,\(\dfrac{C}{B}\).
- Desenhe o gráfico de\(y=A\tan(Bx)\) deslocado para a direita em\(\dfrac{C}{B}\) e para cima em\(D\).
- Esboce as assíntotas\(x=\dfrac{C}{B}+\dfrac{\pi}{| B |}k\), onde\(k\) está um número inteiro.
- Faça um gráfico de três pontos de referência e desenhe o gráfico através desses pontos.
Esboce um gráfico de um período da função\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
Solução
- Etapa 1. A função já está escrita na forma geral\(f(x)=A\cot(Bx−C)+D\).
- Etapa 2. \(A=4\), então o fator de alongamento é\(4\).
- Etapa 3. \(B=\dfrac{\pi}{8}\), então o período é\(P=\dfrac{\pi}{| B |}=\dfrac{\pi}{\dfrac{\pi}{8}}=8\).
- Etapa 4. \(C=\dfrac{\pi}{2}\), então a mudança de fase é\(CB=\dfrac{\dfrac{\pi}{2}}{\dfrac{\pi}{8}}=4\).
- Etapa 5. Nós desenhamos\(f(x)=4\tan \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
- Etapa 6-7. Três pontos que podemos usar para guiar o gráfico são\((6,2)\)\((8,−2)\),\((10,−6)\) e. Usamos a relação recíproca de tangente e cotangente para desenhar\(f(x)=4\cot \left (\dfrac{\pi}{8}x−\dfrac{\pi}{2} \right )−2\).
- Etapa 8. As assíntotas verticais são\(x=4\)\(x=12\) e.
O gráfico é mostrado na Figura\(\PageIndex{21}\).
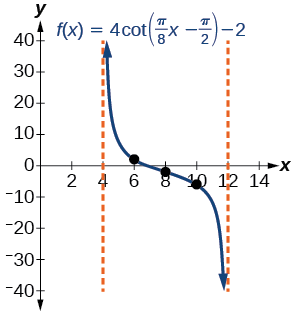
Figura\(\PageIndex{21}\): Um período de uma função cotangente modificada
Usando os gráficos de funções trigonométricas para resolver problemas do mundo real
Muitos cenários do mundo real representam funções periódicas e podem ser modelados por funções trigonométricas. Como exemplo, vamos voltar ao cenário a partir do abridor de seção. Você já observou o feixe formado pela luz giratória em um carro da polícia e se perguntou sobre o movimento do próprio feixe de luz pela parede? O comportamento periódico da distância em que a luz brilha em função do tempo é óbvio, mas como determinamos a distância? Podemos usar a função tangente.
Suponha que a função\(y=5\tan(\dfrac{\pi}{4}t)\) marque a distância no movimento de um feixe de luz do topo de um carro da polícia através de uma parede onde\(t\) está o tempo em segundos e\(y\) é a distância em pés de um ponto na parede diretamente em frente ao carro da polícia.
- Encontre e interprete o fator de alongamento e o período.
- Gráfico do intervalo\([0,5]\).
- Avalie\(f(1)\) e discuta o valor da função nessa entrada.
Solução
- Sabemos, pela forma geral,\(y=A\tan(Bt)\) que\(| A |\) é o fator de alongamento e\(\dfrac{\pi}{B}\) o período.
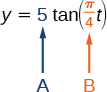
Figura\(\PageIndex{22}\)
Vemos que o fator de alongamento é\(5\). Isso significa que o feixe de luz terá se movido em\(5\) pés após metade do período.
O período é\(\dfrac{\pi}{\tfrac{\pi}{4}}=\dfrac{\pi}{1}⋅\dfrac{4}{\pi}=4\). Isso significa que a cada\(4\) segundo, o feixe de luz varre a parede. A distância do local em frente ao carro da polícia aumenta à medida que o carro da polícia se aproxima.
- Para representar graficamente a função, desenhamos uma assíntota em\(t=2\) e usamos o fator de alongamento e o período. Veja a figura\(\PageIndex{23}\)
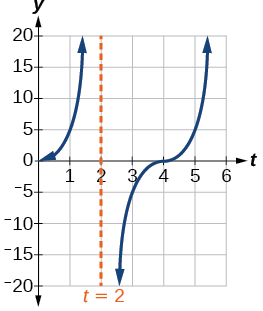
Figura\(\PageIndex{23}\)
- período:\(f(1)=5\tan(\frac{\pi}{4}(1))=5(1)=5\); após o\(1\) segundo, o feixe de se moveu a\(5\) pés do local em frente ao carro da polícia.
Acesse esses recursos on-line para obter instruções e práticas adicionais com gráficos de outras funções trigonométricas.
Equações-chave
| Função tangente deslocada, comprimida e/ou esticada | \(y=A \tan(Bx−C)+D\) |
| Função secante deslocada, comprimida e/ou esticada | \(y=A \sec(Bx−C)+D\) |
| Função cossecante deslocada, comprimida e/ou esticada | \(y=A \csc(Bx−C)+D\) |
| Função cotangente deslocada, comprimida e/ou esticada | \(y=A \cot(Bx−C)+D\) |
Conceitos-chave
- A função tangente tem período\(π\).
- \(f( x )=A\tan( Bx−C )+D\)é uma tangente com alongamento/compressão e deslocamento verticais e/ou horizontais. Veja exemplo\(\PageIndex{1}\)\(\PageIndex{2}\), exemplo e exemplo\(\PageIndex{3}\).
- A secante e a cossecante são funções periódicas com um período de\(2\pi\). \(f( x )=A\sec( Bx−C )+D\)fornece um gráfico de função secante deslocada, comprimida e/ou esticada. Veja o exemplo\(\PageIndex{4}\) e o exemplo\(\PageIndex{5}\).
- \(f( x )=A\csc( Bx−C )+D\)fornece um gráfico da função cossecante deslocada, comprimida e/ou esticada. Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- A função cotangente tem assíntotas menstruais\(\pi\) e verticais em\(0,±\pi,±2\pi\),...
- A faixa de cotangente é\(( −∞,∞ )\), e a função está diminuindo em cada ponto de sua faixa.
- A cotangente é zero em\(±\dfrac{\pi}{2},±\dfrac{3\pi}{2}\),...
- \(f(x)=A\cot(Bx−C)+D\)é uma cotangente com alongamento/compressão e deslocamento verticais e/ou horizontais. Veja o exemplo\(\PageIndex{8}\) e o exemplo\(\PageIndex{9}\).
- Cenários do mundo real podem ser resolvidos usando gráficos de funções trigonométricas. Veja o exemplo\(\PageIndex{10}\).


