6.3: Funções trigonométricas inversas

Objetivos de

• Entenda e use as funções inversas de seno, cosseno e tangente.
• Encontre o valor exato das expressões que envolvem as funções inversas de seno, cosseno e tangente.
• Use uma calculadora para avaliar funções trigonométricas inversas.
• Encontre valores exatos de funções compostas com funções trigonométricas inversas.

Para qualquer triângulo reto, dado um outro ângulo e o comprimento de um lado, podemos descobrir quais são os outros ângulos e lados. Mas e se recebermos apenas dois lados de um triângulo reto? Precisamos de um procedimento que nos leve de uma proporção de lados a um ângulo. É aqui que a noção de uma função inversa a uma trigonométrica entra em jogo. Nesta seção, exploraremos as funções trigonométricas inversas.

Entendendo e usando as funções inversa de seno, cosseno e tangente

Para usar funções trigonométricas inversas, precisamos entender que uma função trigonométrica inversa “desfaz” o que a função trigonométrica original “faz”, como é o caso de qualquer outra função e seu inverso. Em outras palavras, o domínio da função inversa é o intervalo da função original e vice-versa, conforme resumido na Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\)

Por exemplo, se\(f(x)=\sin\space x\), então escreveríamos\(f^{−1}(x)={\sin}^{−1}x\). Esteja ciente de que\({\sin}^{−1}x\) isso não significa\(\dfrac{1}{\sin\space x}\). Os exemplos a seguir ilustram as funções trigonométricas inversas:

• Desde\(\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}\) então\(\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)\).
• Desde\(\cos(\pi)=−1\) então\(\pi={\cos}^{−1}(−1)\).
• Desde\(\tan\left (\dfrac{\pi}{4}\right )=1\) então\(\dfrac{\pi}{4}={\tan}^{−1}(1)\).

Nas seções anteriores, avaliamos as funções trigonométricas em vários ângulos, mas às vezes precisamos saber qual ângulo produziria um valor específico de seno, cosseno ou tangente. Para isso, precisamos de funções inversas. Lembre-se de que, para uma função um-para-um, se\(f(a)=b\), então uma função inversa satisfaria\(f^{−1}(b)=a\).

Lembre-se de que as funções seno, cosseno e tangente não são funções individuais. O gráfico de cada função falharia no teste da linha horizontal. Na verdade, nenhuma função periódica pode ser individual porque cada saída em seu intervalo corresponde a pelo menos uma entrada em cada período e há um número infinito de períodos. Assim como acontece com outras funções que não são individuais, precisaremos restringir o domínio de cada função para gerar uma nova função que seja individual. Escolhemos um domínio para cada função que inclui o número 0. A figura\(\PageIndex{2}\) mostra o gráfico da função seno limitado a\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\) e o gráfico da função cosseno limitado\([ 0,\pi ]\) a.

Figura\(\PageIndex{2}\): (a) Função senoidal em um domínio restrito de\(\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]\); (b) Função cosseno em um domínio restrito de\([ 0,\pi ]\)

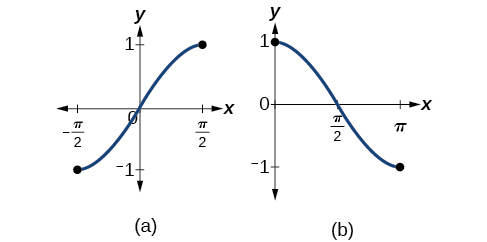
A figura\(\PageIndex{3}\) mostra o gráfico da função tangente limitado\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\) a.

Figura\(\PageIndex{3}\): Função tangente em um domínio restrito de\(\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\)

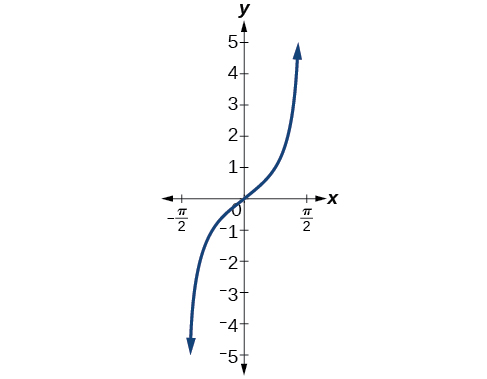
Essas escolhas convencionais para o domínio restrito são um tanto arbitrárias, mas têm características importantes e úteis. Cada domínio inclui a origem e alguns valores positivos e, o mais importante, cada um resulta em uma função individual que é invertível. A escolha convencional para o domínio restrito da função tangente também tem a propriedade útil de se estender de uma assíntota vertical para a próxima, em vez de ser dividida em duas partes por uma assíntota.

Nesses domínios restritos, podemos definir as funções trigonométricas inversas.

• A função senoidal inversa\(y={\sin}^{−1}x\) significa\(x=\sin\space y\). A função seno inverso às vezes é chamada de função arcosseno e notada\(\arcsin\space x\).

  \(y={\sin}^{−1}x\)tem domínio\([−1,1]\) e alcance\(\left[−\frac{\pi}{2},\frac{\pi}{2}\right]\)

• A função inversa do cosseno\(y={\cos}^{−1}x\) significa\(x=\cos\space y\). A função inversa do cosseno às vezes é chamada de função arco-cosseno e anotada\(\arccos\space x\).

  \(y={\cos}^{−1}x\)tem domínio\([−1,1]\) e alcance\([0,π]\)

• A função tangente inversa\(y={\tan}^{−1}x\) significa\(x=\tan\space y\). A função tangente inversa às vezes é chamada de função arco-tangente e notada\(\arctan\space x\).

  \(y={\tan}^{−1}x\)tem domínio\((−\infty,\infty)\) e alcance\(\left(−\frac{\pi}{2},\frac{\pi}{2}\right)\)

Os gráficos das funções inversas são mostrados nas Figuras\(\PageIndex{4}\) -\(\PageIndex{6}\). Observe que a saída de cada uma dessas funções inversas é um número, um ângulo em radianos. Vemos que\({\sin}^{−1}x\) tem domínio\([ −1,1 ]\) e alcance\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\),\({\cos}^{−1}x\) tem domínio\([ −1,1 ]\) e alcance\([0,\pi]\) e\({\tan}^{−1}x\) tem domínio de todos os números e intervalos reais\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\). Para encontrar o domínio e o intervalo das funções trigonométricas inversas, alterne o domínio e o alcance das funções originais. Cada gráfico da função trigonométrica inversa é um reflexo do gráfico da função original sobre a linha\(y=x\).

Figura\(\PageIndex{4}\): A função seno e a função seno inverso (ou arcosseno)

Figura\(\PageIndex{5}\): A função cosseno e a função inversa do cosseno (ou arco-cosseno)

Figura\(\PageIndex{6}\): A função tangente e a função tangente inversa (ou arco-tangente)

RELAÇÕES PARA FUNÇÕES INVERSAS DE SENO, COSSENO E TANGENTE

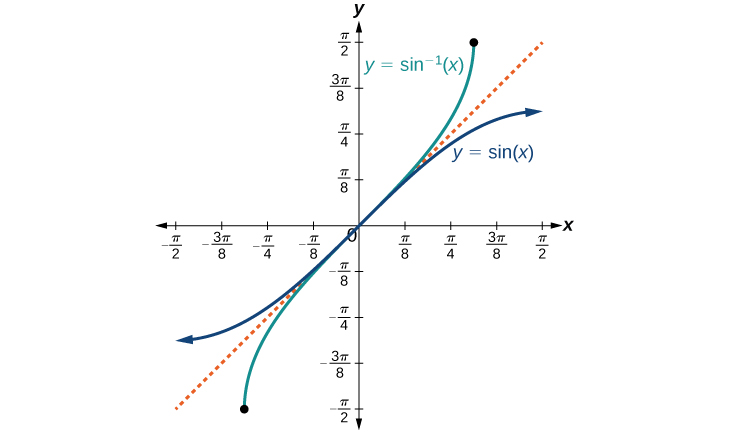
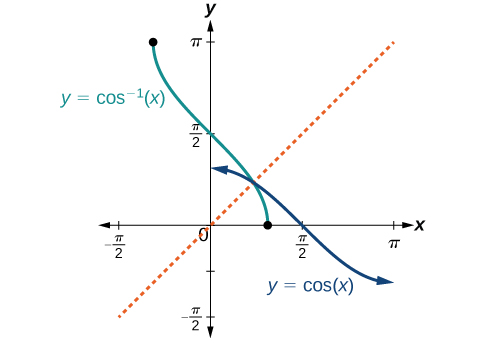
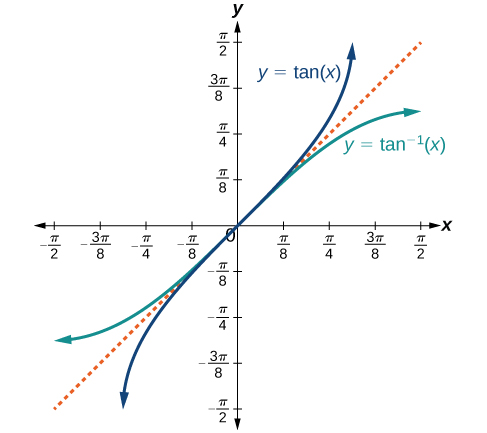
Para ângulos no intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), se\(\sin y=x\), então\({\sin}^{−1}x=y\).

Para ângulos no intervalo\([ 0,\pi ]\), se\(\cos y=x\), então\({\cos}^{−1}x=y\).

Para ângulos no intervalo\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )\), se\(\tan y=x\), então\({\tan}^{−1}x=y\).

Exemplo\(\PageIndex{1}\): Writing a Relation for an Inverse Function

Dado\(\sin\left(\dfrac{5\pi}{12}\right)≈0.96593\), escreva uma relação envolvendo o seno inverso.

Solução

Use a relação para o seno inverso. Se\(\sin y=x\), então\({\sin}^{−1}x=y\).

Nesse problema\(x=0.96593\),\(y=\dfrac{5\pi}{12}\) e.

\({\sin}^{−1}(0.96593)≈\dfrac{5\pi}{12}\)

Exercício\(\PageIndex{1}\)

Dado\(\cos(0.5)≈0.8776\), escreva uma relação envolvendo o cosseno inverso.

Resposta

\(\arccos(0.8776)≈0.5\)

Encontrando o valor exato de expressões envolvendo as funções inversa de seno, cosseno e tangente

Agora que podemos identificar funções inversas, aprenderemos a avaliá-las. Para a maioria dos valores em seus domínios, devemos avaliar as funções trigonométricas inversas usando uma calculadora, interpolando a partir de uma tabela ou usando alguma outra técnica numérica. Assim como fizemos com as funções trigonométricas originais, podemos fornecer valores exatos para as funções inversas quando estamos usando os ângulos especiais, especificamente\(\dfrac{\pi}{6}\) (30°),\(\dfrac{\pi}{4}\) (45°) e\(\dfrac{\pi}{3}\) (60°), e suas reflexões em outros quadrantes.

Dado um valor de entrada “especial”, avalie uma função trigonométrica inversa.

1. Encontre o ângulo\(x\) para o qual a função trigonométrica original tem uma saída igual à entrada dada para a função trigonométrica inversa.
2. Se não\(x\) estiver na faixa definida do inverso, encontre outro ângulo\(y\) que esteja na faixa definida e tenha o mesmo seno, cosseno ou tangente que\(x\), dependendo de qual corresponde à função inversa dada.

Exemplo\(\PageIndex{2}\): Evaluating Inverse Trigonometric Functions for Special Input Values

Avalie cada uma das seguintes opções.

1. \({\sin}^{−1}\left(\dfrac{1}{2}\right)\)
2. \({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)\)
3. \({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)\)
4. \({\tan}^{−1}(1)\)

Solução

1. Avaliar\({\sin}^{−1}\left(\dfrac{1}{2}\right)\) é o mesmo que determinar o ângulo que teria um valor senoidal de\(\dfrac{1}{2}\). Em outras palavras, qual ângulo\(x\) satisfaria\(\sin(x)=\dfrac{1}{2}\)? Existem vários valores que satisfazem essa relação, como\(\dfrac{\pi}{6}\) e\(\dfrac{5\pi}{6}\), mas sabemos que precisamos do ângulo no intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), então a resposta será\({\sin}^{−1}\left (\dfrac{1}{2}\right)=\dfrac{\pi}{6}\). Lembre-se de que o inverso é uma função, portanto, para cada entrada, obteremos exatamente uma saída.
2. Para avaliar\({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)\), sabemos disso\(\dfrac{5\pi}{4}\) e\(\dfrac{7\pi}{4}\) ambos têm um valor senoidal de\(-\dfrac{\sqrt{2}}{2}\), mas nenhum deles está no intervalo\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\). Para isso, precisamos do ângulo negativo coterminal com\(\dfrac{7\pi}{4}\):\({\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\pi}{4}\).
3. Para avaliar\({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)\), estamos procurando um ângulo no intervalo\([ 0,\pi ]\) com um valor de cosseno de\(-\dfrac{\sqrt{3}}{2}\). O ângulo que satisfaz isso é\({\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)=\dfrac{5\pi}{6}\).
4. Avaliando\({\tan}^{−1}(1)\), estamos procurando um ângulo no intervalo\(\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\) com um valor tangente de\(1\). O ângulo correto é\({\tan}^{−1}(1)=\dfrac{\pi}{4}\).

Exercício\(\PageIndex{2}\)

Avalie cada uma das seguintes opções.

1. \({\sin}^{−1}(−1)\)
2. \({\tan}^{−1}(−1)\)
3. \({\cos}^{−1}(−1)\)
4. \({\cos}^{−1}\left(\dfrac{1}{2}\right)\)

Responda a

\(-\dfrac{\pi}{2}\)

Resposta b

\(-\dfrac{\pi}{4}\)

Resposta c

\(\pi\)

Resposta d

\(\dfrac{\pi}{3}\)

Usando uma calculadora para avaliar funções trigonométricas inversas

Para avaliar funções trigonométricas inversas que não envolvem os ângulos especiais discutidos anteriormente, precisaremos usar uma calculadora ou outro tipo de tecnologia. A maioria das calculadoras científicas e aplicativos de emulação de calculadoras tem teclas ou botões específicos para as funções inversa de seno, cosseno e tangente. Eles podem ser rotulados, por exemplo, SIN-1, ARCSIN ou ASIN.

No capítulo anterior, trabalhamos com trigonometria em um triângulo reto para resolver os lados de um triângulo dado um lado e um ângulo adicional. Usando as funções trigonométricas inversas, podemos resolver os ângulos de um triângulo reto dados dois lados e podemos usar uma calculadora para encontrar os valores em várias casas decimais.

Nesses exemplos e exercícios, as respostas serão interpretadas como ângulos e usaremos\(\theta\) como variável independente. O valor exibido na calculadora pode estar em graus ou radianos, portanto, certifique-se de definir o modo apropriado para o aplicativo.

Exemplo\(\PageIndex{3}\): Evaluating the Inverse Sine on a Calculator

Avalie\({\sin}^{−1}(0.97)\) usando uma calculadora.

Solução

Como a saída da função inversa é um ângulo, a calculadora nos fornecerá um valor de grau se estiver no modo grau e um valor em radianos se estiver no modo radiano. As calculadoras também usam as mesmas restrições de domínio nos ângulos que estamos usando.

No modo radiano,\({\sin}^{−1}(0.97)≈1.3252\). No modo de graduação,\({\sin}^{−1}(0.97)≈75.93°\). Observe que, no cálculo e além, usaremos radianos em quase todos os casos.

Exercício\(\PageIndex{3}\)

Avalie\({\cos}^{−1}(−0.4)\) usando uma calculadora.

Resposta

\(1.9823\)ou\(113.578^{\circ}\)

Dados os dois lados de um triângulo reto, como o mostrado na Figura 8.4.7, encontre um ângulo.

Figura\(\PageIndex{7}\)

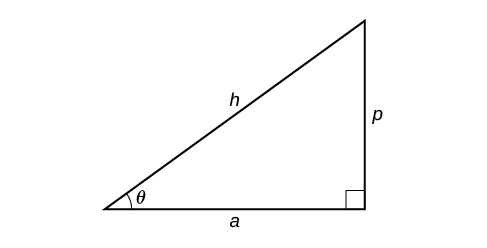
1. Se um determinado lado for a hipotenusa de comprimento\(h\) e o lado de comprimento\(a\) adjacente ao ângulo desejado for fornecido, use a equação\(\theta={\cos}^{−1}\left(\dfrac{a}{h}\right)\).
2. Se um determinado lado for a hipotenusa de comprimento\(h\) e o lado de comprimento\(p\) oposto ao ângulo desejado for fornecido, use a equação\(\theta={\sin}^{−1}\left(\dfrac{p}{h}\right)\).
3. Se as duas pernas (os lados adjacentes ao ângulo reto) forem fornecidas, use a equação\(\theta={\tan}^{−1}\left(\dfrac{p}{a}\right)\).

Exemplo\(\PageIndex{4}\): Applying the Inverse Cosine to a Right Triangle

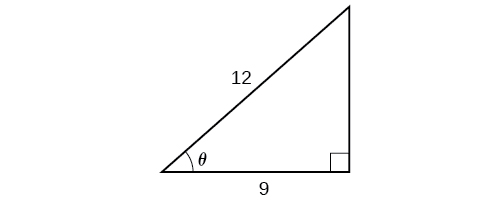
Resolva o triângulo na Figura\(\PageIndex{8}\) para o ângulo\(\theta\).

Figura\(\PageIndex{8}\)

Solução

Como conhecemos a hipotenusa e o lado adjacente ao ângulo, faz sentido usarmos a função cosseno.

\[\begin{align*} \cos \theta&= \dfrac{9}{12}\\ \theta&= {\cos}^{-1}\left(\dfrac{9}{12}\right)\qquad \text{Apply definition of the inverse}\\ \theta&\approx 0.7227\qquad \text{or about } 41.4096^{\circ} \text{ Evaluate} \end{align*}\]

Exercício\(\PageIndex{4}\)

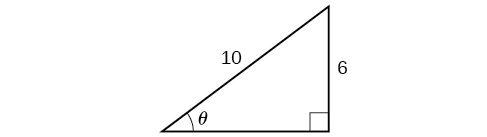
Resolva o triângulo na Figura\(\PageIndex{9}\) para o ângulo\(\theta\).

Figura\(\PageIndex{9}\)

Resposta

\({\sin}^{−1}(0.6)=36.87°=0.6435\)radianos

Encontrando valores exatos de funções compostas com funções trigonométricas inversas

Há momentos em que precisamos compor uma função trigonométrica com uma função trigonométrica inversa. Nesses casos, geralmente podemos encontrar valores exatos para as expressões resultantes sem recorrer a uma calculadora. Mesmo quando a entrada para a função composta é uma variável ou uma expressão, muitas vezes podemos encontrar uma expressão para a saída. Para ajudar a resolver casos diferentes,\(f(x)\)\(g(x)\) sejam duas funções trigonométricas diferentes pertencentes ao conjunto {\(\sin(x)\),\(\cos(x)\),\(\tan(x)\)}\(f^{-1}(y)\) e\(g^{-1}(y)\) sejam suas inversas.

Avaliando composições do formulário\(f(f^{-1}(y))\) e\(f^{-1}(f(x))\)

Para qualquer função trigonométrica,\(f(f^{-1}(y))=y\) para todos\(y\) no domínio adequado para a função dada. Isso decorre da definição do inverso e do fato de que a faixa de\(f\) foi definida como idêntica ao domínio de\(f^{−1}\). No entanto, precisamos ter um pouco mais de cuidado com as expressões do formulário\(f^{-1}(f(x))\).

COMPOSIÇÕES DE UMA FUNÇÃO TRIGONOMÉTRICA E SEU INVERSO

\[\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}\]

PERGUNTAS E RESPOSTAS

É correto isso\({\sin}^{−1}(\sin x)=x\)?

Não. Essa equação está correta se x pertence ao domínio restrito\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), mas o seno é definido para todos os valores reais de entrada e,\(x\) fora do intervalo restrito, a equação não está correta porque seu inverso sempre retorna um valor em\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\). A situação é semelhante para cosseno e tangente e seus inversos. Por exemplo,\({\sin}^{−1}\left(\sin\left(\dfrac{3\pi}{4}\right)\right)=\dfrac{\pi}{4}\).

Dada uma expressão do formulário\(f^{-1}(f(\theta))\) where \(f(\theta)=\sin \theta\), \(\cos \theta\), or \(\tan \theta\), evaluate.

1. Se\(\theta\) estiver no domínio restrito de\(f\), então\(f^{−1}(f(\theta))=\theta\).
2. Caso contrário, encontre um ângulo\(\phi\) dentro do domínio restrito de tal forma que\(f(\phi)=f(\theta)\). Então\(f^{−1}(f(\theta))=\phi\).

Exemplo\(\PageIndex{5}\): Using Inverse Trigonometric Functions

Avalie o seguinte:

1. \({\sin}^{−1}\left (\sin \left(\dfrac{\pi}{3}\right )\right )\)
2. \({\sin}^{−1}\left (\sin \left(\dfrac{2\pi}{3}\right )\right )\)
3. \({\cos}^{−1}\left (\cos \left (\dfrac{2\pi}{3}\right )\right )\)
4. \({\cos}^{−1}\left (\cos \left (−\dfrac{\pi}{3}\right )\right )\)

Solução

1. \(\dfrac{\pi}{3}\)está dentro\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), então\({\sin}^{−1}\left(\sin\left(\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}\).
2. \(\dfrac{2\pi}{3}\)não está em\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), mas\(sin\left(\dfrac{2\pi}{3}\right)=sin\left(\dfrac{\pi}{3}\right)\), então\({\sin}^{−1}\left(\sin\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{\pi}{3}\).
3. \(\dfrac{2\pi}{3}\)está dentro\([ 0,\pi ]\), então\({\cos}^{−1}\left(\cos\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{2\pi}{3}\).
4. \(-\dfrac{\pi}{3}\)não está presente\([ 0,\pi ]\), mas\(\cos\left(−\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{3}\right)\) porque o cosseno é uma função uniforme. \(\dfrac{\pi}{3}\)está dentro\([ 0,\pi ]\), então\({\cos}^{−1}\left(\cos\left(−\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}\).

Exercício\(\PageIndex{5}\)

Avalie\({\tan}^{−1}\left(\tan\left(\dfrac{\pi}{8}\right)\right)\)\({\tan}^{−1}\left(\tan\left(\dfrac{11\pi}{9}\right)\right)\) e.

Resposta

\(\dfrac{\pi}{8}\);\(\dfrac{2\pi}{9}\)

Avaliando as composições do formulário\(f^{-1}(g(x))\)

Agora que podemos compor uma função trigonométrica com seu inverso, podemos explorar como calcular a composição de uma função trigonométrica e o inverso de outra função trigonométrica. Começaremos com as composições do formulário\(f^{-1}(g(x))\). Para valores especiais de\(x\), podemos calcular exatamente a função interna e, em seguida, a função externa inversa. No entanto, podemos encontrar uma abordagem mais geral considerando a relação entre os dois ângulos agudos de um triângulo reto onde um está\(\theta\), tornando o outro\(\dfrac{\pi}{2}−\theta\). Considere o seno e o cosseno de cada ângulo do triângulo reto na Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): Triângulo reto ilustrando as relações de cofunção

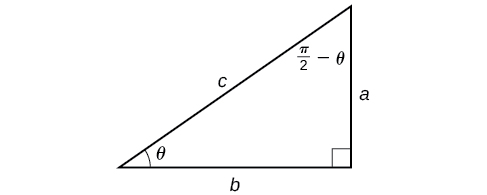
Porque\(\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)\), nós temos\({\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta\) isso\(0≤\theta≤\pi\). Se não\(\theta\) estiver nesse domínio, precisamos encontrar outro ângulo que tenha o mesmo cosseno\(\theta\) e pertença ao domínio restrito; então subtraímos esse ângulo de\(\dfrac{\pi}{2}\) .Similarmente\(\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)\), então\({\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta\) se\(−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}\). Essas são apenas as relações função-co-função apresentadas de outra forma.

Funções dadas do formulário\({\sin}^{−1}(\cos x)\) and \({\cos}^{−1}(\sin x)\), evaluate them.

1. Se\(x\) está dentro\([ 0,\pi ]\), então\({\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x\).
2. Se não\(x\) estiver dentro\([ 0,\pi ]\), então encontre outro ângulo\(y\) para que\(\cos y=\cos x\).\([ 0,\pi ]\)

   \[{\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y\]

3. Se\(x\) está dentro\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), então\({\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x\).
4. Se não\(x\) estiver dentro\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\), então encontre outro ângulo\(y\) para que\(\sin y=\sin x\).\(\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]\)

   \[{\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y\]

Exemplo\(\PageIndex{6}\): Evaluating the Composition of an Inverse Sine with a Cosine

Avalie\({\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)\)

1. por avaliação direta.
2. pelo método descrito anteriormente.

Solução

1. Aqui, podemos avaliar diretamente o interior da composição. \[\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}\]Agora, podemos calcular a função inversa como fizemos anteriormente. \[{\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}\]
2. Nós temos\(x=\dfrac{13\pi}{6}\)\(y=\dfrac{\pi}{6}\), e\[\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}\]

Exercício\(\PageIndex{6}\)

Avalie\({\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )\).

Resposta

\(\dfrac{3\pi}{4}\)

Avaliando as composições do formulário\(f(g^{−1}(x))\)

Para avaliar composições da forma\(f(g^{−1}(x))\), onde\(f\) e\(g\) são quaisquer duas das funções seno, cosseno ou tangente e\(x\) é qualquer entrada no domínio de\(g^{−1}\), temos fórmulas exatas, como\(\sin({\cos}^{−1}x)=\sqrt{1−x^2}\). Quando precisamos usá-las, podemos derivar essas fórmulas usando as relações trigonométricas entre os ângulos e lados de um triângulo reto, juntamente com o uso da relação de Pitágoras entre os comprimentos dos lados. Podemos usar a identidade pitagórica,\({\sin}^2 x+{\cos}^2 x=1\), para resolver uma quando dada a outra. Também podemos usar as funções trigonométricas inversas para encontrar composições envolvendo expressões algébricas.

Exemplo\(\PageIndex{7}\): Evaluating the Composition of a Sine with an Inverse Cosine

Encontre um valor exato para\(\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)\).

Solução

Começando pelo interior, podemos dizer que existe algum ângulo como esse\(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\), o que significa\(\cos \theta=\dfrac{4}{5}\), e estamos procurando\(\sin \theta\). Podemos usar a identidade pitagórica para fazer isso.

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}\]

Como\(\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )\) está no quadrante I,\(\sin \theta\) deve ser positivo, então a solução é\(35\). Veja a Figura\(\PageIndex{11}\).

Figura\(\PageIndex{11}\): Triângulo reto ilustrando que se\(\cos \theta=\dfrac{4}{5}\), então\(\sin \theta=\dfrac{3}{5}\)

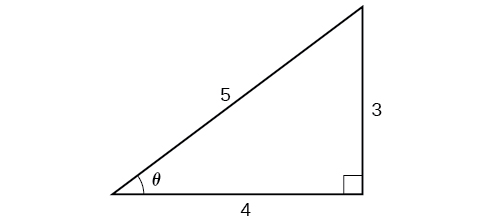
Sabemos que o cosseno inverso sempre fornece um ângulo no intervalo\([ 0,\pi ]\), então sabemos que o seno desse ângulo deve ser positivo; portanto\(\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}\).

Exercício\(\PageIndex{7}\)

Avalie\(\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )\).

Resposta

\(\frac{12}{13}\)

Exemplo\(\PageIndex{8}\): Evaluating the Composition of a Sine with an Inverse Tangent

Encontre um valor exato para\(\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)\).

Solução

Embora possamos usar uma técnica semelhante à do Exemplo\(\PageIndex{6}\), demonstraremos uma técnica diferente aqui. De dentro, sabemos que existe um ângulo como esse\(\tan \theta=\dfrac{7}{4}\). Podemos imaginar isso como os lados opostos e adjacentes em um triângulo reto, conforme mostrado na Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\): Um triângulo reto com dois lados conhecidos

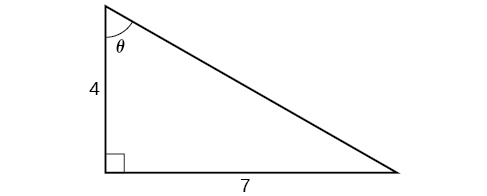
Usando o Teorema de Pitágoras, podemos encontrar a hipotenusa desse triângulo.

\ [\ begin {align*}
4^2+7^2&= {hipotenusa} ^2\\
hypotenuse&=\ sqrt {65}
\\ text {Agora, podemos calcular o seno do ângulo como o lado oposto dividido pela hipotenusa.} \\
\ sin\ theta&=\ dfrac {7} {\ sqrt {65}}\\
\ text {Isso nos dá a composição desejada.} \\
\ sin\ left ({\ tan} ^ {-1}\ left (\ dfrac {7} {4}\ right)\ right) &=\ sin\ theta\\
&=\ dfrac {7} {\ sqrt {65}}\\
&=\ dfrac {7\ sqrt {65}} {65}
\ end {align*}\]

Exercício\(\PageIndex{8}\)

Avalie\(\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)\).

Resposta

\(\dfrac{4\sqrt{2}}{9}\)

Exemplo\(\PageIndex{9}\): Finding the Cosine of the Inverse Sine of an Algebraic Expression

Encontre uma expressão simplificada\(\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)\) para for\(−3≤x≤3\).

Solução

Sabemos que existe um ângulo\(\theta\) como esse\(\sin \theta=\dfrac{x}{3}\).

\[\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}\]

Como sabemos que o seno inverso deve fornecer um ângulo no intervalo\([ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]\), podemos deduzir que o cosseno desse ângulo deve ser positivo.

\(cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}\)

Exercício\(\PageIndex{9}\)

Encontre uma expressão simplificada para\(\sin({\tan}^{−1}(4x))\) for \(−\dfrac{1}{4}≤x≤\dfrac{1}{4}\).

Resposta

\(\dfrac{4x}{\sqrt{16x^2+1}}\)

Mídia

Acesse este recurso on-line para obter instruções e práticas adicionais com funções trigonométricas inversas.

• Avalie expressões envolvendo funções trigonométricas inversas

Visite este site para obter mais perguntas práticas do Learningpod.

Conceitos-chave

• Uma função inversa é aquela que “desfaz” outra função. O domínio de uma função inversa é o intervalo da função original e o intervalo de uma função inversa é o domínio da função original.
• Como as funções trigonométricas não são individuais em seus domínios naturais, as funções trigonométricas inversas são definidas para domínios restritos.
• Para qualquer função trigonométrica\(f(x)\), if\(x=f^{−1}(y)\), then\(f(x)=y\). No entanto,\(f(x)=y\) só implica\(x=f^{−1}(y)\) se\(x\) estiver no domínio restrito de\(f\). Veja o exemplo\(\PageIndex{1}\).
• Ângulos especiais são as saídas de funções trigonométricas inversas para valores de entrada especiais; por exemplo,\(\frac{\pi}{4}={\tan}^{−1}(1)\)\(\frac{\pi}{6}={\sin}^{−1}(\frac{1}{2})\) e. Consulte Exemplo\(\PageIndex{2}\).
• Uma calculadora retornará um ângulo dentro do domínio restrito da função trigonométrica original. Veja o exemplo\(\PageIndex{3}\).
• As funções inversas nos permitem encontrar um ângulo quando dados os dois lados de um triângulo reto. Veja o exemplo\(\PageIndex{4}\).
• Na composição da função, se a função interna for uma função trigonométrica inversa, então há expressões exatas; por exemplo,\(\sin({\cos}^{−1}(x))=\sqrt{1−x^2}\). Veja o exemplo\(\PageIndex{5}\).
• Se a função interna for uma função trigonométrica, as únicas combinações possíveis são\({\sin}^{−1}(\cos x)=\frac{\pi}{2}−x\) se\(0≤x≤\pi\) e\({\cos}^{−1}(\sin x)=\frac{\pi}{2}−x\) se\(−\frac{\pi}{2}≤x≤\frac{\pi}{2}\). Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
• Ao avaliar a composição de uma função trigonométrica com uma função trigonométrica inversa, desenhe um triângulo de referência para ajudar a determinar a proporção de lados que representa a saída da função trigonométrica. Veja o exemplo\(\PageIndex{8}\).
• Ao avaliar a composição de uma função trigonométrica com uma função trigonométrica inversa, você pode usar identidades trigonométricas para ajudar a determinar a proporção dos lados. Veja o exemplo\(\PageIndex{9}\).