6.1: Gráficos das funções seno e cosseno
- Page ID
- 189179
- Variações gráficas de\(y=\sin( x )\)\(y=\cos( x )\) e.
- Use mudanças de fase das curvas seno e cosseno.
A luz branca, como a luz do sol, não é realmente branca. Em vez disso, é uma composição de todas as cores do arco-íris na forma de ondas. As cores individuais só podem ser vistas quando a luz branca passa por um prisma óptico que separa as ondas de acordo com seus comprimentos de onda para formar um arco-íris.

As ondas de luz podem ser representadas graficamente pela função seno. No capítulo sobre Funções trigonométricas, examinamos funções trigonométricas, como a função seno. Nesta seção, vamos interpretar e criar gráficos das funções seno e cosseno.
Representação gráfica de funções senoidais e cossenos
Lembre-se de que as funções seno e cosseno relacionam valores de números reais às\(y\) coordenadas\(x\) - e -de um ponto no círculo unitário. Então, como eles se parecem em um gráfico em um plano coordenado? Vamos começar com a função seno. Podemos criar uma tabela de valores e usá-los para esboçar um gráfico. A tabela\(\PageIndex{1}\) lista alguns dos valores da função seno em um círculo unitário.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\sin(x)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) |
Traçar os pontos da tabela e continuar ao longo do eixo x dá a forma da função seno. Veja a Figura\(\PageIndex{2}\).
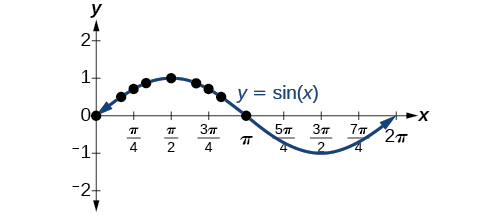
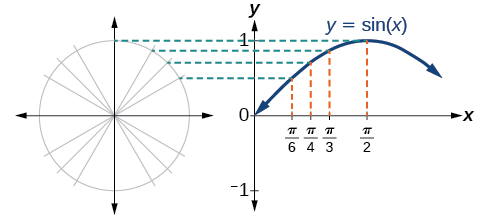
Observe como os valores do seno são positivos entre\(0\) e\(\pi\), que correspondem aos valores da função seno nos quadrantes I e II no círculo unitário, e os valores do seno são negativos entre\(\pi\) e\(2\pi\), que correspondem aos valores da função seno nos quadrantes III e IV no círculo unitário. Veja a Figura\(\PageIndex{3}\).
Agora, vamos dar uma olhada semelhante na função do cosseno. Novamente, podemos criar uma tabela de valores e usá-los para esboçar um gráfico. A tabela\(\PageIndex{2}\) lista alguns dos valores da função cosseno em um círculo unitário.
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(\cos(x)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) | \(0\) | \(-\dfrac{1}{2}\) | \(-\dfrac{\sqrt{2}}{2}\) | \(-\dfrac{\sqrt{3}}{2}\) | \(-1\) |
Assim como na função seno, podemos traçar pontos para criar um gráfico da função cosseno, como na Figura\(\PageIndex{4}\).
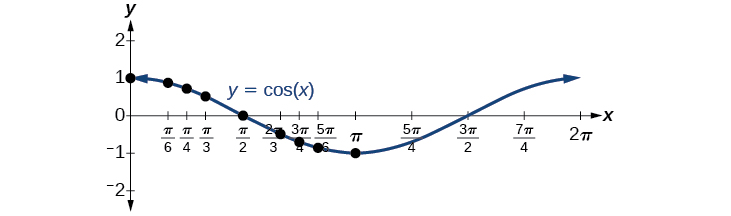
Como podemos calcular o seno e o cosseno de qualquer número real, essas duas funções são definidas para todos os números reais. Ao pensar nos valores de seno e cosseno como coordenadas de pontos em um círculo unitário, fica claro que o intervalo de ambas as funções deve ser o intervalo\([ −1,1 ]\).
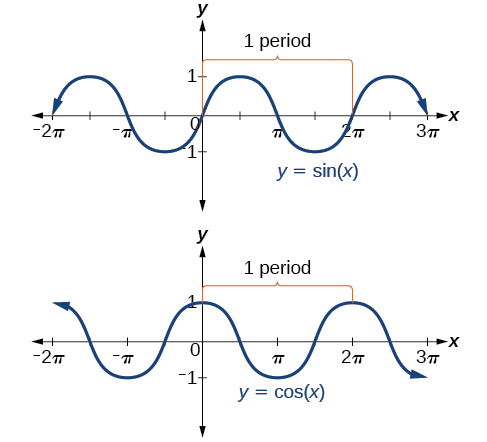
Em ambos os gráficos, a forma do gráfico se repete depois\(2\pi\), o que significa que as funções são periódicas com um período de\(2\pi\). Uma função periódica é uma função para a qual um deslocamento horizontal específico\(P\),, resulta em uma função igual à função original:\(f(x+P)=f(x)\) para todos os valores de\(x\) no domínio de\(f\). Quando isso ocorre, chamamos a menor mudança horizontal desse tipo com\(P>0\) o período da função. A figura\(\PageIndex{5}\) mostra vários períodos das funções seno e cosseno.
Analisar novamente as funções seno e cosseno em um domínio centrado no\(y\) eixo -ajuda a revelar simetrias. Como podemos ver na Figura\(\PageIndex{6}\), a função seno é simétrica em relação à origem. Lembre-se de As Outras Funções Trigonométricas que determinamos a partir do círculo unitário que a função seno é uma função ímpar porque\(\sin(−x)=−\sin\space x\). Agora podemos ver claramente essa propriedade no gráfico.
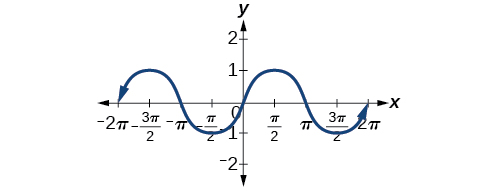
A figura\(\PageIndex{7}\) mostra que a função cosseno é simétrica em relação ao\(y\) eixo y. Novamente, determinamos que a função cosseno é uma função par. Agora podemos ver no gráfico que\(\cos(−x)=\cos\space x\).
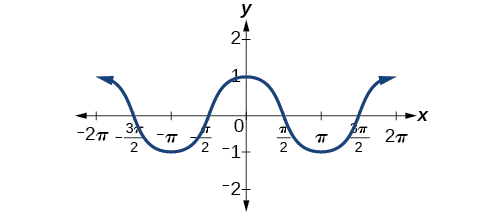
As funções seno e cosseno têm várias características distintas:
- São funções periódicas com um período de\(2\pi\).
- O domínio de cada função é\((−\infty,\infty)\) e o intervalo é\([ −1,1 ]\).
- O gráfico de\(y=\sin\space x\) é simétrico em relação à origem, porque é uma função ímpar.
- O gráfico de\(y=\cos\space x\) é simétrico em relação ao\(y\) eixo deles, porque é uma função uniforme.
Investigando funções sinusoidais
Como podemos ver, as funções seno e cosseno têm um período e um intervalo regulares. Se observarmos ondas oceânicas ou ondulações em um lago, veremos que elas se assemelham às funções seno ou cosseno. No entanto, eles não são necessariamente idênticos. Alguns são mais altos ou mais longos do que outros. Uma função que tem a mesma forma geral de uma função seno ou cosseno é conhecida como função senoidal. As formas gerais de funções senoidais são
\[y=A\sin(Bx−C)+D\]
e
\[y=A\cos(Bx−C)+D\]
Determinando o período das funções sinusoidais
Observando as formas das funções senoidais, podemos ver que elas são transformações das funções seno e cosseno. Podemos usar o que sabemos sobre transformações para determinar o período.
Na fórmula geral,\(B\) está relacionado ao período de\(P=\dfrac{2\pi}{|B|}\). Se\(|B|>1\), então o período é menor que\(2\pi\) e a função sofre uma compressão horizontal, enquanto se\(| B |<1\), então o período é maior que\(2\pi\) e a função sofre um alongamento horizontal. Por exemplo,\(f(x)=\sin(x)\),\(B=1\), então o período é\(2\pi\), o que nós sabíamos. Se\(f(x)=\sin(2x)\), então\(B=2\), o período é\(\pi\) e o gráfico é compactado. Se\(f(x)=\sin\left(\dfrac{x}{2}\right)\), então\(B=\dfrac{1}{2}\), o período é\(4\pi\) e o gráfico é esticado. Observe na Figura\(\PageIndex{8}\) como o período está indiretamente relacionado\(|B|\) a.
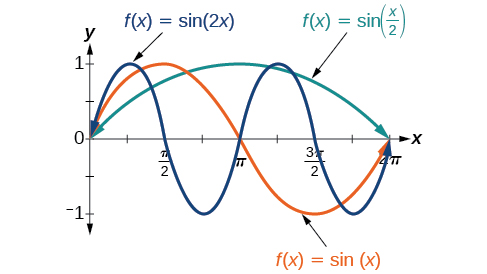
Se deixarmos\(C=0\) e\(D=0\) na forma geral equações das funções seno e cosseno, obtemos as formas
- \(y=A\sin(Bx)\)
- \(y=A\cos(Bx)\)
O período é\(\dfrac{2\pi}{|B|}\).
Determine o período da função\(f(x)=\sin\left(\dfrac{\pi}{6}x\right)\).
Solução
Vamos começar comparando a equação com a forma geral\(y=A\sin(Bx)\).
Na equação dada\(B=\dfrac{\pi}{6}\), então o período será
\[ \begin{align*} P&=\dfrac{2\pi}{|B|} \\[4pt] &=\dfrac{2\pi}{\dfrac{\pi}{6}} \\ &=2\pi ⋅ \dfrac{6}{\pi} \\[4pt] &=12 \end{align*}\]
Determine o período da função\(g(x)=\cos(\frac{x}{3})\).
- Resposta
-
\(6\pi\)
Determinando a amplitude
Voltando à fórmula geral de uma função senoidal, analisamos como a variável\(B\) se relaciona com o período. Agora, vamos voltar para a variável para que\(A\) possamos analisar como ela está relacionada à amplitude ou à maior distância do repouso. \(A\)representa o fator de estiramento vertical e seu valor absoluto\(|A|\) é a amplitude. Os máximos locais serão uma distância\(|A|\) acima da linha média vertical do gráfico, que é a linha\(x=D\); porque\(D=0\) nesse caso, a linha média é o eixo x. Os mínimos locais serão a mesma distância abaixo da linha média. Se\(| A |>1\), a função está esticada. Por exemplo, a amplitude de\(f(x)=4 sin x\) é o dobro da amplitude de
\(f(x)=2\sin x\)
Se\(| A |<1\), a função está comprimida. A figura\(\PageIndex{9}\) compara várias funções senoidais com diferentes amplitudes.
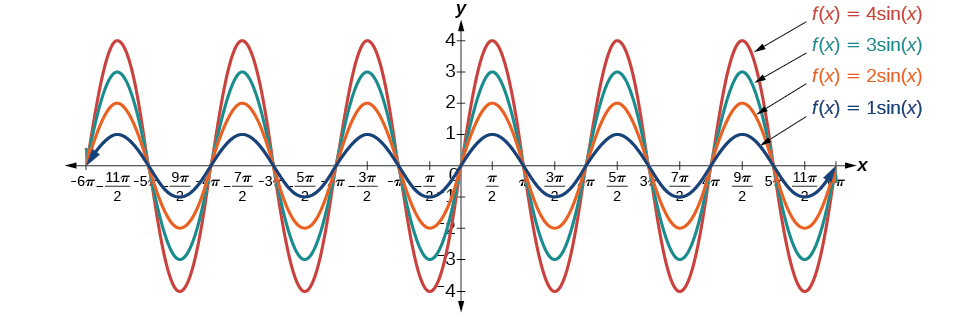
Se deixarmos\(C=0\) e\(D=0\) na forma geral equações das funções seno e cosseno, obtemos as formas
\[\begin{align} y=A\sin(Bx)\text { and } y=A\cos(Bx) \end{align}\]
A amplitude é\(A\), e a altura vertical da linha média é\(|A|\). Além disso, observe no exemplo que
\[|A| = amplitude = \dfrac{1}{2}∣maximum − minimum|\]
Qual é a amplitude da função senoidal\(f(x)=−4\sin(x)\)? A função está esticada ou comprimida verticalmente?
Solução
Vamos começar comparando a função com a forma simplificada\(y=A\sin(Bx)\).
Na função dada,\(A=−4\), então a amplitude é\(| A |=| −4 |=4\). A função está ampliada.
Análise
O valor negativo de\(A\) resulta em uma reflexão sobre o\(x\) eixo -da função seno, conforme mostrado na Figura\(\PageIndex{10}\).
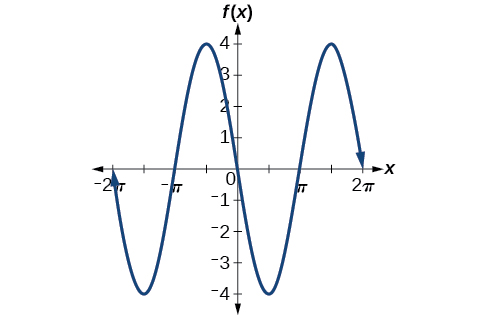
Qual é a amplitude da função senoidal\(f(x)=\frac{1}{2}\sin(x)\)? A função está esticada ou comprimida verticalmente?
- Responda
-
\(\frac{1}{2}\)comprimido
Analisando gráficos de variações de\(y = \sin\space x\) e\(y = \cos\space x\)
Agora que entendemos como\(A\) e nos\(B\) relacionamos com a equação de forma geral para as funções seno e cosseno, exploraremos as variáveis\(C\)\(D\) e. Lembre-se da forma geral:
\[y=A\sin(Bx-C)+D\qquad \text{ and } \qquad y=A\cos(Bx-C)+D\]
ou
\[y=A\sin\left (B\left (x-\dfrac{C}{B} \right ) \right )+D \qquad \text{ and } \qquad y=A\cos\left (B\left (x-\dfrac{C}{B} \right ) \right )+D\]
O valor\(\frac{C}{B}\) de uma função senoidal é chamado de mudança de fase ou deslocamento horizontal da função básica de seno ou cosseno. Se\(C>0\), o gráfico muda para a direita. Se\(C<0\), o gráfico muda para a esquerda. Quanto maior o valor de\(| C |\), mais o gráfico é deslocado. A figura\(\PageIndex{11}\) mostra que o gráfico de\(f(x)=\sin(x−\pi)\) deslocamentos para a direita em\(\pi\) unidades, o que é mais do que vemos no gráfico de\(f(x)=\sin\left(x−\frac{\pi}{4}\right)\), que se desloca para a direita em\(\frac{\pi}{4}\) unidades.
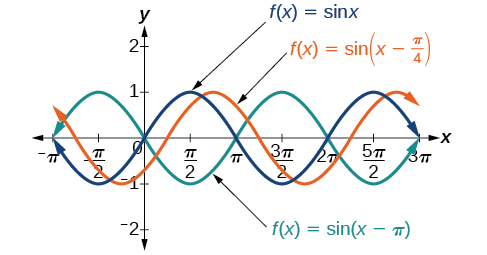
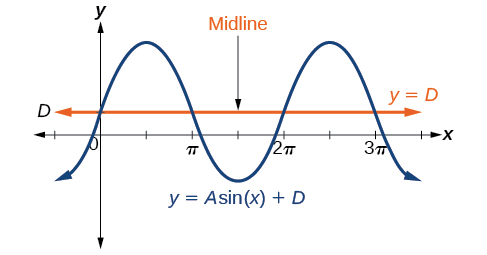
Enquanto\(C\) se relaciona com o deslocamento horizontal,\(D\) indica o deslocamento vertical da linha média na fórmula geral para uma função senoidal. Veja a Figura\(\PageIndex{12}\). A função\(y=\cos(x)+D\) tem sua linha média em\(y=D\).
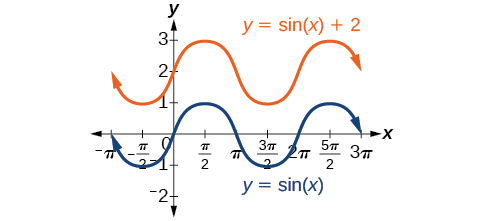
Qualquer valor\(D\) diferente de zero desloca o gráfico para cima ou para baixo. A figura\(\PageIndex{13}\) se compara\(f(x)=\sin x\) com\(f(x)=\sin x+2\), que é deslocada\(2\) unidades para cima em um gráfico.
Dada uma equação na forma\(f(x)=A \sin (Bx−C)+D\) ou\(f(x)=A \cos (Bx−C)+D\),\(\frac{C}{D}\) é a mudança de fase e\(D\) é a mudança vertical.
Determine a direção e a magnitude da mudança de fase para\(f(x)=\sin\left(x+\frac{\pi}{6}\right)−2\).
Solução
Vamos começar comparando a equação com a forma geral\(y=A\sin(Bx−C)+D\).
Na equação dada, observe que\(B=1\)\(C=−\frac{\pi}{6}\) e. Portanto, a mudança de fase é
\[\begin{align*} \dfrac{C}{B}&= -\frac{\frac{\pi}{6}}{1}\\ &= -\frac{\pi}{6} \end{align*}\]
ou\(\frac{\pi}{6}\) unidades à esquerda.
Análise
Devemos prestar atenção ao sinal na equação da forma geral de uma função senoidal. A equação mostra um sinal de menos antes\(C\). Portanto,\(f(x)=\sin(x+\frac{\pi}{6})−2\) pode ser reescrito como\(f(x)=\sin\left(x−\left(−\frac{\pi}{6}\right)\right)−2\). Se o valor de\(C\) for negativo, a mudança será para a esquerda.
Determine a direção e a magnitude da mudança de fase para\(f(x)=3\cos\left(x−\frac{\pi}{2}\right)\).
- Responda
-
\(\frac{\pi}{2}\); certo
Determine a direção e a magnitude do deslocamento vertical para\(f(x)=\cos(x)−3\).
Solução
Vamos começar comparando a equação com a forma geral\(y=A\cos(Bx−C)+D\).
Na equação dada,\(D=−3\) então a mudança é de\(3\) unidades para baixo.
Determine a direção e a magnitude do deslocamento vertical para\(f(x)=3\sin(x)+2\).
- Responda
-
\(2\)unidades acima
- Determine a amplitude como\(| A |\).
- Determine o período como\(P=\frac{2\pi}{| B |}\).
- Determine a mudança de fase como\(\frac{C}{B}\).
- Determine a linha média como\(y=D\).
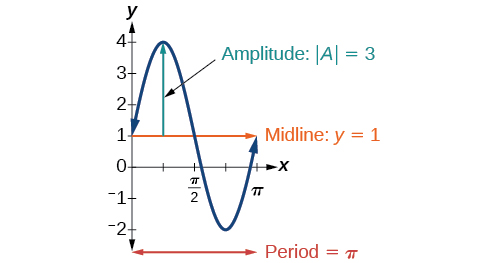
Determine a linha média, a amplitude, o período e a mudança de fase da função\(y=3\sin (2x)+1\).
Solução
Vamos começar comparando a equação com a forma geral\(y=A\sin (Bx−C)+D\).
\(A=3\), então a amplitude é\(| A |=3\).
Em seguida\(B=2\), então o período é\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{2}=\pi\).
Não há nenhuma constante adicionada dentro dos parênteses, então\(C=0\) e a mudança de fase é\(\dfrac{C}{B}=\dfrac{0}{2}=0\).
Finalmente,\(D=1\), então a linha média é\(y=1\).
Análise
Inspecionando o gráfico, podemos determinar se o período é\(\pi\), a linha média é\(y=1\) e a amplitude é\(3\). Veja a Figura\(\PageIndex{14}\).
Determine a linha média, a amplitude, o período e a mudança de fase da função\(y=\frac{1}{2}\cos \left(\frac{x}{3}−\frac{\pi}{3}\right)\).
- Responda
-
linha média:\(y=0\); amplitude:\(| A |=\frac{1}{2}\); período:\(P=\frac{2\pi}{| B |}=6π\); mudança de fase:\(\frac{C}{B}=\pi\)
Determine a fórmula para a função cosseno na Figura\(\PageIndex{15}\).
![Um gráfico de -0,5 cos (x) +0,5. O gráfico tem uma amplitude de 0,5. O gráfico tem um período de 2pi. O gráfico tem um intervalo de [0, 1]. O gráfico também é refletido sobre o eixo x da função principal cos (x).](https://math.libretexts.org/@api/deki/files/6903/CNX_Precalc_Figure_06_01_015.jpg)
Solução
Para determinar a equação, precisamos identificar cada valor na forma geral de uma função senoidal.
\(y=A\sin (Bx−C)+D\)
\(y=A\cos (Bx−C)+D\)
O gráfico pode representar uma função senoidal ou cosseno que é deslocada e/ou refletida. Quando\(x=0\), o gráfico tem um ponto extremo,\((0,0)\). Como a função cosseno tem um ponto extremo para\(x=0\), vamos escrever nossa equação em termos de uma função cosseno.
Vamos começar com a linha média. Podemos ver que o gráfico sobe e desce a uma distância igual acima e abaixo\(y=0.5\). Esse valor, que é a linha média, está\(D\) na equação, então\(D=0.5\).
A maior distância acima e abaixo da linha média é a amplitude. Os máximos são\(0.5\) unidades acima da linha média e os mínimos são\(0.5\) unidades abaixo da linha média. Então\(| A |=0.5\). Outra forma de determinar a amplitude é reconhecendo que a diferença entre a altura dos máximos e mínimos locais é\(1\), portanto\(| A |=\frac{1}{2}=0.5\). Além disso, o gráfico é refletido sobre o\(x\) eixo -, de modo que\(A=−0.5\).
Portanto, o gráfico não está esticado ou comprimido horizontalmente\(B=1\); e o gráfico não é deslocado horizontalmente, portanto\(C=0\).
Juntando tudo isso,
\(g(x)=−0.5\cos (x)+0.5\)
Determine a fórmula para a função seno na Figura\(\PageIndex{16}\).
![Um gráfico de sin (x) +2. Período de 2pi, amplitude de 1 e faixa de [1, 3].](https://math.libretexts.org/@api/deki/files/6904/CNX_Precalc_Figure_06_01_016.jpg)
- Responda
-
\(f(x)=\sin(x)+2\)
Determine a equação para a função senoidal na Figura\(\PageIndex{17}\).
![Um gráfico de 3cos (pi/3x-pi/3) -2. O gráfico tem amplitude de 3, período de 6, intervalo de [-5,1].](https://math.libretexts.org/@api/deki/files/6905/CNX_Precalc_Figure_06_01_017.jpg)
Solução
Com o valor mais alto em\(1\) e o menor valor em\(−5\), a linha média estará a meio caminho entre em\(−2\). Então\(D=−2\).
A distância da linha média até o valor mais alto ou mais baixo fornece uma amplitude de\(| A |=3\).
O período do gráfico é\(6\), que pode ser medido do pico em\(x=1\) até o próximo pico em\(x=7\), ou da distância entre os pontos mais baixos. Portanto,\(P=\dfrac{2\pi}{| B |}=6\). Usando o valor positivo para\(B\), descobrimos que
\[\begin{align*} B&=\dfrac{2\pi}{P}\\ &=\dfrac{2\pi}{6}\\ &=\dfrac{\pi}{3} \end{align*}\]
Até agora, nossa equação é\(y=3\sin\left(\dfrac{\pi}{3}x−C\right)−2\) ou\(y=3\cos\left(\dfrac{\pi}{3}x−C\right)−2\) .Para a forma e a mudança, temos mais de uma opção. Poderíamos escrever isso como qualquer um dos seguintes:
- um cosseno deslocado para a direita
- um cosseno negativo deslocado para a esquerda
- um seno deslocado para a esquerda
- um seno negativo se deslocou para a direita
Embora qualquer um deles esteja correto, os deslocamentos de cosseno são mais fáceis de trabalhar do que os deslocamentos senoidais nesse caso porque envolvem valores inteiros. Então nossa função se torna
\[\begin{align*} y&=3\cos \left (\frac{\pi}{3}x-\dfrac{\pi}{3} \right )-2 \qquad \text{or} \\ y&=-3\cos \left (\dfrac{\pi}{3}x+\dfrac{2\pi}{3} \right )-2 \end{align*}\]
Novamente, essas funções são equivalentes, então ambas produzem o mesmo gráfico.
Escreva uma fórmula para a função representada graficamente na Figura\(\PageIndex{18}\).
![Um gráfico de 4sin ((pi/5) x-pi/5) +4. O gráfico tem período de 10, amplitude de 4, intervalo de [0,8].](https://math.libretexts.org/@api/deki/files/6906/CNX_Precalc_Figure_06_01_018n.jpg)
- Responda
-
duas possibilidades:\(y=4\sin\left(\dfrac{\pi}{5}x−\dfrac{\pi}{5}\right)+4\) ou\(y=−4\sin\left(\dfrac{\pi}{5}x+\dfrac{4\pi}{5}\right)+4\)
Representação gráfica de variações de\(y = \sin\space x\) e\(y = \cos\space x\)
Ao longo desta seção, aprendemos sobre os tipos de variações das funções seno e cosseno e usamos essas informações para escrever equações a partir de gráficos. Agora podemos usar as mesmas informações para criar gráficos a partir de equações.
Em vez de focar nas equações de forma geral
\(y=A\sin(Bx-C)+D \text{ and } y=A\cos(Bx-C)+D\)
vamos deixar\(C=0\)\(D=0\) e trabalhar com uma forma simplificada das equações nos exemplos a seguir.
- Identifique a amplitude,\(| A |\).
- Identifique o período,\(P=\dfrac{2\pi}{| B |}\).
- Comece na origem, com a função aumentando para a direita se\(A\) for positivo ou diminuindo se\(A\) for negativo.
- Em\(x=\dfrac{\pi}{2| B |}\) há um máximo local para\(A>0\) ou um mínimo para\(A<0\), com\(y=A\).
- A curva retorna ao eixo x em\(x=\dfrac{\pi}{| B |}\).
- Há um mínimo local para\(A>0\) (máximo para\(A<0\)) em\(x=\dfrac{3\pi}{2| B |}\) com\(y=–A\).
- A curva retorna novamente para o eixo x em\(x=\dfrac{\pi}{2| B |}\).
Esboce um gráfico de\(f(x)=−2\sin\left(\dfrac{\pi x}{2}\right)\).
Solução
Vamos começar comparando a equação com o formulário\(y=A\sin(Bx)\).
- Etapa 1. Podemos ver pela equação que\(A=−2\), então a amplitude é 2.
\(|A|=2 \)
- Etapa 2. A equação mostra que\(B=\dfrac{\pi}{2}\), então o período é
\[\begin{align*} P&=\dfrac{2\pi}{\dfrac{\pi}{2}}\\ &=2\pi \cdot \dfrac{2}{\pi}\\ &=4 \end{align*}\]
- Etapa 3. Como\(A\) é negativo, o gráfico desce à medida que nos movemos para a direita da origem.
- Etapa 4. Os\(x\) interceptos -estão no início de um período\(x=0\), os pontos médios horizontais estão em\(x=2\) e no final de um período em\(x=4\).
Os quartos de pontos incluem o mínimo em\(x=1\) e o máximo em\(x=3\). Um mínimo local ocorrerá\(2\) unidades abaixo da linha média, em\(x=1\), e um máximo local ocorrerá em\(2\) unidades acima da linha média, em\(x=3\). A figura\(\PageIndex{19}\) mostra o gráfico da função.
![Um gráfico de -2sin ((pi/2) x). O gráfico tem alcance de [-2,2], período de 4 e amplitude de 2.](https://math.libretexts.org/@api/deki/files/6907/CNX_Precalc_Figure_06_01_019.jpg)
Esboce um gráfico de\( g(x)=−0.8\cos(2x)\). Determine a linha média, a amplitude, o período e a mudança de fase.
- Responda
-
![Um gráfico de -0,8 cos (2x). O gráfico tem alcance de [-0,8, 0,8], período de pi, amplitude de 0,8 e é refletido sobre o eixo x em comparação com sua função principal cos (x).](https://math.libretexts.org/@api/deki/files/6908/CNX_Precalc_Figure_06_01_020.jpg)
Figura\(\PageIndex{20}\) linha média:\(y=0\); amplitude:\(| A |=0.8\); período:\(P=\dfrac{2\pi}{| B |}=\pi\); mudança de fase:\(\dfrac{C}{B}=0\) ou nenhuma
- Expresse a função na forma geral\(y=A\sin(Bx−C)+D\) ou\(y=A\cos(Bx−C)+D\).
- Identifique a amplitude,\(| A |\).
- Identifique o período,\(P=\dfrac{2\pi}{| B |}\).
- Identifique a mudança de fase,\(\dfrac{C}{B}\).
- Desenhe o gráfico de\(f(x)=A\sin(Bx)\) deslocado para a direita ou esquerda em\(\dfrac{C}{B}\) e para cima ou para baixo em\(D\).
Esboce um gráfico de\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\).
Solução
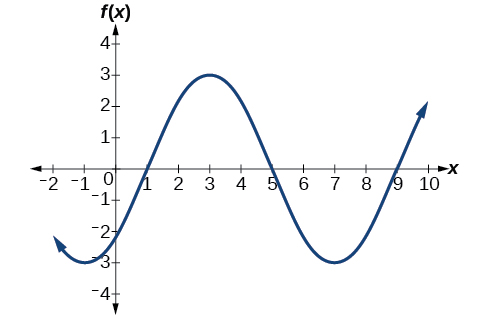
- Etapa 1. A função já está escrita na forma geral:\(f(x)=3\sin\left(\dfrac{\pi}{4x}−\dfrac{\pi}{4}\right)\) .Este gráfico terá a forma de uma função senoidal, começando na linha média e aumentando para a direita.
- Etapa 2. \(| A |=| 3 |=3\). A amplitude é\(3\).
- Etapa 3. Desde então\(| B |=| \dfrac{\pi}{4} |=\dfrac{\pi}{4}\), determinamos o período da seguinte forma.
\[\begin{align*} P&=\dfrac{2\pi}{|B|}\\ &=\dfrac{2\pi}{\dfrac{\pi}{4}}\\ &=2\pi \cdot \dfrac{4}{\pi}\\ &=8 \end{align*}\]
O período é\(8\).
- Etapa 4. Desde então\(C=\dfrac{\pi}{4}\), a mudança de fase é
\[\dfrac{C}{B}=\dfrac{\dfrac{\pi}{4}}{\dfrac{\pi}{4}}=1\].
A mudança de fase é\(1\) unitária.
- Etapa 5. A figura\(\PageIndex{21}\) mostra o gráfico da função.
Desenhe um gráfico de\(g(x)=−2\cos\left(\dfrac{\pi}{3}x+\dfrac{\pi}{6}\right)\). Determine a linha média, a amplitude, o período e a mudança de fase.
- Responda
-
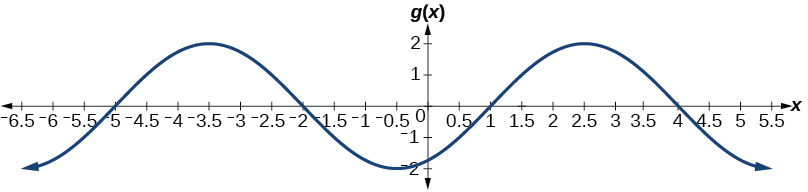
Figura\(\PageIndex{22}\) linha média:\(y=0\); amplitude:\(| A |=2\); período:\(P=\dfrac{2\pi}{| B |}=6\); mudança de fase:\(\dfrac{C}{B}=−\dfrac{1}{2}\)
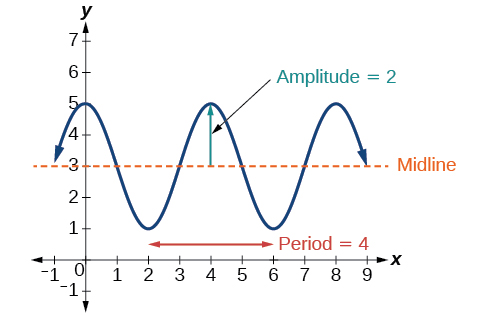
Dado\(y=−2cos\left(\dfrac{\pi}{2}x+\pi\right)+3\), determine a amplitude, o período, a mudança de fase e a mudança horizontal. Em seguida, faça um gráfico da função.
Solução
Comece comparando a equação com a forma geral.
\(y=A\cos(Bx−C)+D\)
- Etapa 1. A função já está escrita em formato geral.
- Etapa 2. Desde então\(A=−2\), a amplitude é\(| A |=2\).
- Etapa 3. \(| B |=\dfrac{\pi}{2}\), então o período é\(P=\dfrac{2\pi}{| B |}=\dfrac{2\pi}{\dfrac{pi}{2}}=2\pi⋅\dfrac{2}{\pi}=4\). O período é 4.
- Etapa 4. \(C=−\pi\), então calculamos a mudança de fase como\(\dfrac{C}{B}=−\dfrac{\pi}{\dfrac{\pi}{2}}=−\pi⋅\dfrac{2}{\pi}=−2\). A mudança de fase é\(−2\).
- Etapa 5. \(D=3\), então a linha média é\(y=3\) e o deslocamento vertical está para cima\(3\).
Como\(A\) é negativo, o gráfico da função cosseno foi refletido sobre o\(x\) eixo y.
A figura\(\PageIndex{23}\) mostra um ciclo do gráfico da função.
Usando transformações das funções seno e cosseno
Podemos usar as transformações das funções seno e cosseno em várias aplicações. Conforme mencionado no início do capítulo, o movimento circular pode ser modelado usando a função seno ou cosseno.
Um ponto gira em torno de um círculo de raio\(3\) centrado na origem. Esboce um gráfico da\(y\) coordenada -do ponto em função do ângulo de rotação.
Solução
Lembre-se de que, para um ponto em um círculo de raio\(r\), a\(y\) coordenada -do ponto é\(y=r \sin(x)\), então, neste caso, obtemos a equação\(y(x)=3 \sin(x)\). A constante\(3\) causa um alongamento vertical dos\(y\) valores -da função por um fator de\(3\), que podemos ver no gráfico da Figura\(\PageIndex{24}\).
![Um gráfico de 3sin (x). O gráfico tem período de 2pi, amplitude de 3 e alcance de [-3,3].](https://math.libretexts.org/@api/deki/files/6912/CNX_Precalc_Figure_06_01_023.jpg)
Análise
Observe que o período da função ainda é\(2\pi\); à medida que viajamos ao redor do círculo, retornamos ao ponto\((3,0)\) de\(x=2\pi,4\pi,6\pi,\)... Como as saídas do gráfico agora oscilarão entre\(–3\) e\(3\), a amplitude da onda senoidal é\(3\).
Qual é a amplitude da função\(f(x)=7\cos(x)\)? Esboce um gráfico dessa função.
- Responda
-
![Um gráfico de 7cos (x). O gráfico tem amplitude de 7, período de 2pi e alcance de [-7,7].](https://math.libretexts.org/@api/deki/files/6913/CNX_Precalc_Figure_06_01_024.jpg)
Figura\(\PageIndex{25}\)
Um círculo com raio\(3\) ft é montado com o centro\(4\) pés fora do solo. O ponto mais próximo do solo é rotulado\(P\), conforme mostrado na Figura\(\PageIndex{26}\). Esboce um gráfico da altura acima do solo do ponto à\(P\) medida que o círculo é girado; em seguida, encontre uma função que forneça a altura em termos do ângulo de rotação.
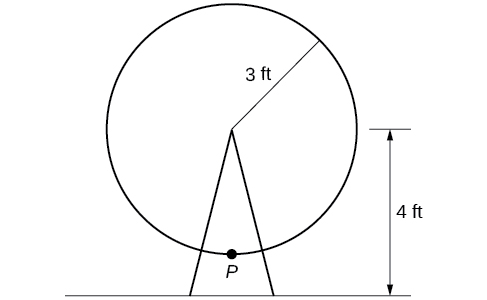
Solução
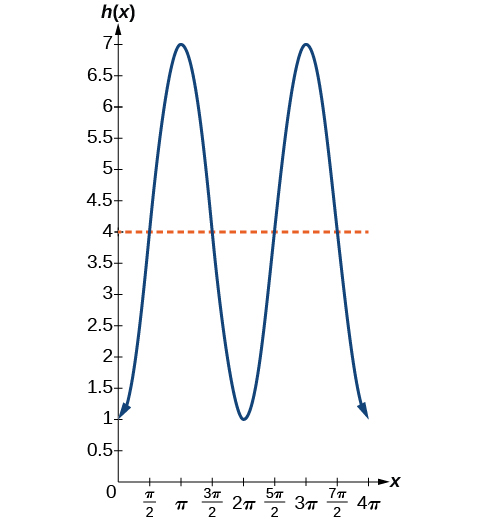
Esboçando a altura, notamos que ela começará\(1\) pés acima do solo, depois aumentará até\(7\) pés acima do solo e continuará a oscilar\(3\) pés acima e abaixo do valor central de\(4\) pés, conforme mostrado na Figura\(\PageIndex{27}\).
Embora pudéssemos usar uma transformação da função seno ou cosseno, começamos procurando características que tornariam uma função mais fácil de usar do que a outra. Vamos usar uma função de cosseno porque ela começa com o valor mais alto ou mais baixo, enquanto uma função seno começa no valor médio. Um cosseno padrão começa no valor mais alto, e esse gráfico começa no valor mais baixo, então precisamos incorporar uma reflexão vertical.
Segundo, vemos que o gráfico oscila\(3\) acima e abaixo do centro, enquanto um cosseno básico tem uma amplitude de\(1\), então esse gráfico foi esticado verticalmente\(3\), como no último exemplo.
Finalmente, para mover o centro do círculo até uma altura de\(4\), o gráfico foi deslocado verticalmente\(4\). Juntando essas transformações, descobrimos que
\(y=−3\cos(x)+4\)
Um peso é preso a uma mola que é então pendurada em uma placa, conforme mostrado na Figura\(\PageIndex{28}\). À medida que a mola oscila para cima e para baixo, a posição\(y\) do peso\(–1\) em relação à prancha varia de dentro. (no momento\(x=0\)) para\(–7\) entrar. (no momento\(x=π\)) abaixo do tabuleiro. Suponha que a posição de\(y\) seja dada como uma função senoidal de\(x\). Esboce um gráfico da função e, em seguida, encontre uma função de cosseno que forneça a posição\(y\) em termos de\(x\).
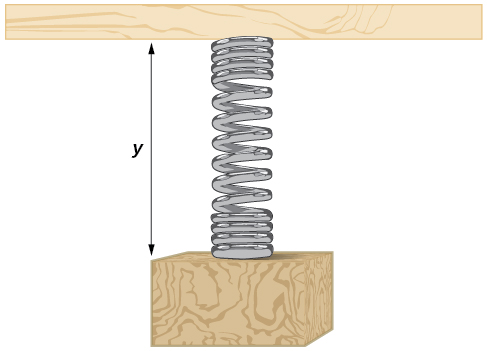
- Responda
-
\(y=3\cos(x)−4\)
![Um gráfico de cosseno com intervalo [-1, -7]. O período é de 2 pi. Máximos locais em (0, -1), (2pi, -1) e (4pi, -1). Mínimos locais em (pi, -7) e (3pi, -7).](https://math.libretexts.org/@api/deki/files/6917/CNX_Precalc_Figure_06_01_027.jpg)
Figura\(\PageIndex{29}\)
A London Eye é uma enorme roda gigante com um diâmetro de\(135\) metros (\(443\)pés). Ele completa uma rotação a cada\(30\) minuto. Os pilotos embarcam de uma plataforma\(2\) metros acima do solo. Expresse a altura do ciclista acima do solo em função do tempo em minutos.
Solução
Com um diâmetro de\(135\) m, a roda tem um raio de\(67.5\) m. A altura oscilará com a amplitude\(67.5\) m acima e abaixo do centro.
Os passageiros embarcam\(2\) m acima do nível do solo, então o centro da roda deve estar localizado\(67.5+2=69.5\) m acima do nível do solo. A linha média da oscilação estará em\(69.5\) m.
A roda leva\(30\) minutos para completar a\(1\) rotação, então a altura oscilará com um período de\(30\) minutos.
Por fim, como o piloto embarca no ponto mais baixo, a altura começará no menor valor e aumentará, seguindo a forma de uma curva de cosseno refletida verticalmente.
- Amplitude:\(67.5\), então\(A=67.5\)
- Linha média:\(69.5\), então\(D=69.5\)
- Período:\(30\), então\(B=\dfrac{2\pi}{30}=\dfrac{\pi}{15}\)
- Forma:\(−\cos(t)\)
Uma equação para a altura do ciclista seria
\(y=−67.5\cos\left(\dfrac{\pi}{15}t\right)+69.5\)
onde\(t\) está em minutos e\(y\) é medido em metros.
Acesse esses recursos on-line para obter instruções e práticas adicionais com gráficos das funções do seno e do cosseno.
- Amplitude e período de seno e cosseno
- Traduções de Sine and Cosine
- Representação gráfica de transformações senoidais e cossenos
- Representação gráfica da função seno
Equações-chave
| Funções sinusoidais |
\(f(x)=A\sin(Bx−C)+D\) \(f(x)=A\cos(Bx−C)+D\) |
Conceitos-chave
- As funções periódicas se repetem após um determinado valor. O menor valor desse tipo é o período. As funções básicas do seno e do cosseno têm um período de\(2\pi\).
- A função\(\sin x\) é ímpar, então seu gráfico é simétrico em relação à origem. A função\(\cos x\) é uniforme, então seu gráfico é simétrico em relação ao eixo y.
- O gráfico de uma função senoidal tem a mesma forma geral de uma função seno ou cosseno.
- Na fórmula geral para uma função senoidal, o período é\(P=\dfrac{2\pi}{| B |}\). Veja o exemplo\(\PageIndex{1}\).
- Na fórmula geral para uma função senoidal,\( | A |\) representa a amplitude. Se\(| A |>1\), a função é esticada, enquanto se\(| A |<1\), a função é comprimida. Veja o exemplo\(\PageIndex{2}\).
- O valor\(\dfrac{C}{B}\) na fórmula geral para uma função senoidal indica a mudança de fase. Veja o exemplo\(\PageIndex{3}\).
- O valor\(D\) na fórmula geral para uma função senoidal indica o deslocamento vertical da linha média. Veja o exemplo\(\PageIndex{4}\).
- Combinações de variações das funções senoidais podem ser detectadas a partir de uma equação. Veja o exemplo\(\PageIndex{5}\).
- A equação para uma função senoidal pode ser determinada a partir de um gráfico. Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- Uma função pode ser representada graficamente identificando sua amplitude e período. Veja o exemplo\(\PageIndex{8}\) e o exemplo\(\PageIndex{9}\).
- Uma função também pode ser representada graficamente identificando sua amplitude, período, mudança de fase e deslocamento horizontal. Veja o exemplo\(\PageIndex{10}\).
- As funções sinusoidais podem ser usadas para resolver problemas do mundo real. Veja exemplo\(\PageIndex{11}\)\(\PageIndex{12}\), exemplo e exemplo\(\PageIndex{13}\).


