Home
Idioma Portugues
Pré-cálculo (OpenStax)
13: Funções trigonométricas
13.2: Círculo unitário - Funções de seno e cosseno

13.2: Círculo unitário - Funções de seno e cosseno

Last updated
Save as PDF

Page ID: 189234

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Encontre valores de função para o seno e o cosseno de 30° ou$(\frac{\pi}{6})$ ,45° ou$(\frac{\pi}{4})$, e 60° ou$(\frac{\pi}{3})$.
Identifique o domínio e o intervalo das funções seno e cosseno.
Encontre ângulos de referência.
Use ângulos de referência para avaliar funções trigonométricas.

Procurando por uma emoção? Em seguida, considere um passeio na Singapore Flyer, a roda gigante mais alta do mundo. Localizada em Cingapura, a roda gigante atinge uma altura de 541 pés — pouco mais de um décimo de milha! Descrita como uma roda de observação, os ciclistas desfrutam de vistas espetaculares enquanto viajam do solo até o pico e descem novamente em um padrão repetido. Nesta seção, examinaremos esse tipo de movimento giratório em torno de um círculo. Para fazer isso, precisamos definir primeiro o tipo de círculo e depois colocar esse círculo em um sistema de coordenadas. Em seguida, podemos discutir o movimento circular em termos dos pares de coordenadas.

Foto de uma roda gigante. — Figura$\PageIndex{1}$: O Singapore Flyer é a roda gigante mais alta do mundo. (crédito: “Vibin JK” /Flickr)

Encontrando valores de função para o seno e o cosseno

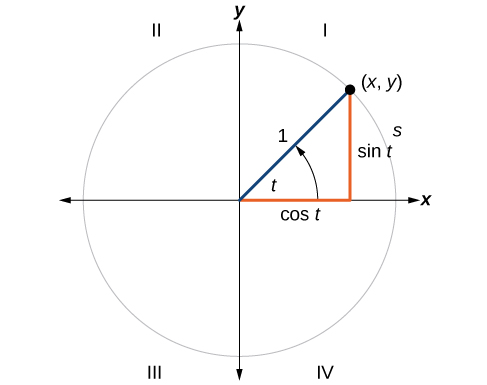
Para definir nossas funções trigonométricas, começamos desenhando um círculo unitário, um círculo centrado na origem com raio 1, conforme mostrado na Figura$\PageIndex{2}$. O ângulo (em radianos) que$t$ intercepta forma um arco de comprimento$s$. Usando a fórmula$s=rt$, e sabendo disso$r=1$, vemos isso para um círculo unitário,$s=t$.

Lembre-se de que os eixos x e y dividem o plano coordenado em quatro quartos chamados quadrantes. Rotulamos esses quadrantes para imitar a direção que um ângulo positivo varreria. Os quatro quadrantes são rotulados como I, II, III e IV.

Para qualquer ângulo,$t,$ podemos rotular a interseção do lado do terminal e do círculo unitário por suas coordenadas,$(x,y)$. As coordenadas$x$ e$y$ serão as saídas das funções trigonométricas$f(t)= \cos t$ e$ f(t)= \sin t$, respectivamente. Isso significa$x= \cos t$$y= \sin t$ e.

Gráfico de um círculo com ângulo t, raio de 1 e um arco criado pelo ângulo com comprimento s. O lado terminal do ângulo cruza o círculo no ponto (x, y). — Figura$\PageIndex{2}$: Círculo unitário em que o ângulo central é$t$ radianos

CÍRCULO UNI

Um círculo unitário tem um centro em$(0,0)$ e um raio$1$. Em um círculo unitário, o comprimento do arco interceptado é igual à medida radiana do ângulo central$1$.

$(x,y)$Seja o ponto final no círculo unitário de um arco de comprimento de arco$s$. As$(x,y)$ coordenadas desse ponto podem ser descritas como funções do ângulo.

Definindo funções de seno e cosseno

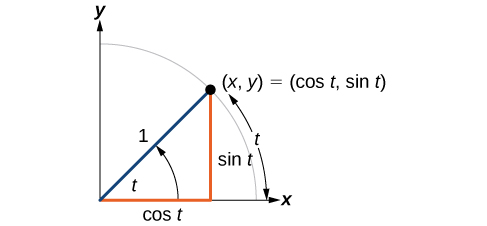
Agora que temos nosso círculo unitário rotulado, podemos aprender como as$(x,y)$ coordenadas se relacionam com o comprimento e o ângulo do arco. A função seno relaciona um número real$t$ com a coordenada y do ponto em que o ângulo correspondente intercepta o círculo unitário. Mais precisamente, o seno de um ângulo$t$ é igual ao valor y da extremidade no círculo unitário de um arco de comprimento$t$. Na Figura$\PageIndex{3}$, o seno é igual$y$ a. Como todas as funções, a função seno tem uma entrada e uma saída. Sua entrada é a medida do ângulo; sua saída é a coordenada y do ponto correspondente no círculo unitário.

A função cosseno de um ângulo$t$ é igual ao valor x da extremidade no círculo unitário de um arco de comprimento$t$. Na Figura$\PageIndex{1}$, o cosseno é igual a x.

Ilustração de um ângulo t, com comprimento do lado terminal igual a 1 e um arco criado por ângulo com comprimento t. O lado terminal do ângulo cruza o círculo no ponto (x, y), que é equivalente a (cos t, sin t). — Figura$\PageIndex{3}$

Como se entende que seno e cosseno são funções, nem sempre precisamos escrevê-los com parênteses:$\sin t$ é o mesmo$\sin (t)$ e$\cos t$ é o mesmo que$\cos (t)$. Da mesma forma,$\cos ^2 t$ é uma notação abreviada comumente usada para$( \cos (t))^2$. Esteja ciente de que muitas calculadoras e computadores não reconhecem a notação abreviada. Em caso de dúvida, use os parênteses extras ao inserir cálculos em uma calculadora ou computador.

FUNÇÕES DE SENO E COSSENO

Se$t$ for um número real e um ponto$(x,y)$ no círculo unitário corresponder a um ângulo de$t$, então

\[ \begin{align} \cos t & = x \\ \sin t & = y \end{align}\]

COMO: Dado um ponto$P(x,y)$ on the unit circle corresponding to an angle of $ t$, find the sine and cosine

O seno de$t$ é igual à coordenada y do ponto$P: \sin t=y$.
O cosseno de$t$ é igual à coordenada x do ponto$P: \cos t=x$.

Exemplo$\PageIndex{1}$: Finding Function Values for Sine and Cosine

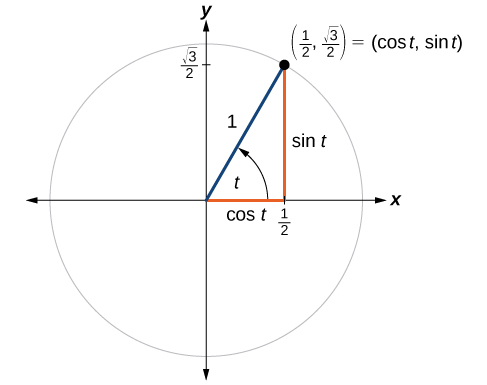
Ponto$P$ é um ponto no círculo unitário correspondente a um ângulo de$t$, conforme mostrado na Figura$\PageIndex{4}$. Encontre$\cos (t)$$\sin (t)$ e.

Gráfico de um círculo com ângulo t, raio de 1 e um lado terminal que cruza o círculo no ponto (1/2, raiz quadrada de 3 sobre 2). — Figura$\PageIndex{4}$

Solução

Sabemos que$\cos t $ é a coordenada x do ponto correspondente no círculo unitário e$\sin t$ é a coordenada y do ponto correspondente no círculo unitário. Então:

\[\begin{align} x & = \cos t= \frac{1}{2} \\ y & = \sin t= \frac{\sqrt{3}}{2} \end{align}\]

Exercício$\PageIndex{1}$:

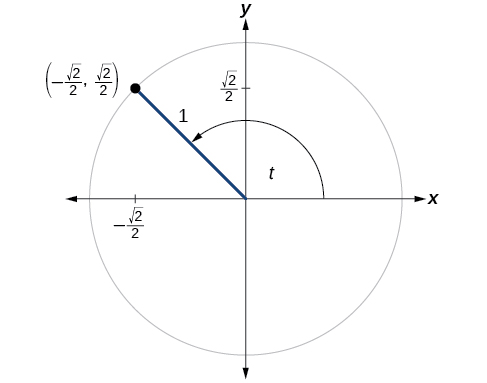
Um certo ângulo$t$ corresponde a um ponto no círculo unitário$(−\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$, conforme mostrado na Figura$\PageIndex{5}$. Encontre$\cos t$$\sin t$ e.

Gráfico de um círculo com ângulo t, raio de 1 e um lado terminal que cruza o círculo no ponto (raiz quadrada negativa de 2 sobre 2, raiz quadrada de 2 sobre 2). — Figura$\PageIndex{5$

Solução

\[\cos (t)=−\frac{ \sqrt{2} }{2}, \sin (t)=\frac {\sqrt{2}}{2} \]

Encontrando senos e cossenos de ângulos em um eixo

Para ângulos quadrantrais, o ponto correspondente no círculo unitário cai no eixo x ou y. Nesse caso, podemos calcular facilmente o cosseno e o seno a partir dos valores de$x$$y$ e.

Exemplo$\PageIndex{2}$: Calculating Sines and Cosines along an Axis

Encontre$\cos (90°)$ e$\sin (90°).$

Solução

Mover-se$90°$ no sentido anti-horário ao redor do círculo unitário a partir do eixo x positivo nos leva ao topo do círculo, onde estão as$(x,y)$ coordenadas (0, 1), conforme mostrado na Figura$\PageIndex{6}$.

Gráfico de um círculo com ângulo t, raio de 1 e um lado terminal que cruza o círculo no ponto (0,1). — Figura$\PageIndex{6}$

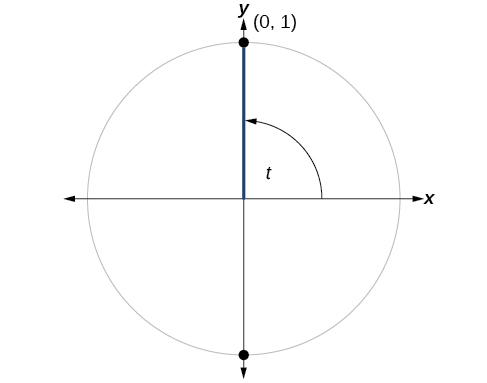
Usando nossas definições de cosseno e seno,

\[\begin{align} x & \cos t = \cos (90°) = 0 \\ y & \sin t = \sin (90°) = 1 \end{align}\]

O cosseno de 90° é 0; o seno de 90° é 1.

Exercício$\PageIndex{2}$

Encontre o cosseno e o seno do ângulo$π$.

Solução

$\cos (π)=−1, \sin (π)=0$

A identidade pitagórica

Agora que podemos definir seno e cosseno, aprenderemos como eles se relacionam entre si e com o círculo unitário. Lembre-se de que a equação para o círculo unitário é$x^2+y^2=1$. Porque$x= \cos t$ e$y=\sin t$, podemos substituir$ x$ e$y$ obter$\cos ^2 t+ \sin ^2 t=1.$ Essa equação,$ \cos ^2 t+ \sin ^2 t=1,$ é conhecida como Identidade Pitagórica. Veja a Figura$\PageIndex{7}$.

Gráfico de um ângulo t, com um ponto (x, y) no círculo unitário. E a equação mostrando a equivalência de 1, x^2 + y^2 e cos^2 t + sin^2 t. — Figura$\PageIndex{7}$

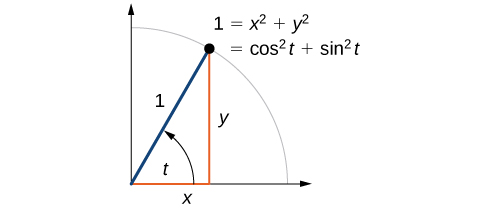
Podemos usar a identidade pitagórica para encontrar o cosseno de um ângulo se conhecermos o seno, ou vice-versa. No entanto, como a equação produz duas soluções, precisamos de conhecimento adicional do ângulo para escolher a solução com o sinal correto. Se soubermos o quadrante onde está o ângulo, podemos escolher facilmente a solução correta.

IDENTIDADE PITAGÓRICA

A identidade pitagórica afirma que, para qualquer número real$t$,

\[ \cos^2 t+ \sin^2 t=1\]

como: Dado o seno de algum ângulo t e sua localização no quadrante, encontre o cosseno de t

Substitua o valor conhecido de$\sin (t)$ na identidade pitagórica.
Resolver para$ \cos (t)$.
Escolha a solução com o sinal apropriado para os valores de x no quadrante em que t t está localizado.

Exemplo$\PageIndex{3}$: Finding a Cosine from a Sine or a Sine from a Cosine

Se$\sin (t)=\frac{3}{7}$ e$t$ estiver no segundo quadrante, encontre$ \cos (t)$.

Solução

Se derrubarmos uma linha vertical do ponto no círculo unitário correspondente a$t$, criaremos um triângulo reto, a partir do qual podemos ver que a identidade de Pitágoras é simplesmente um caso do Teorema de Pitágoras. Veja a Figura$\PageIndex{8}$.

Gráfico de um círculo unitário com um ângulo que cruza o círculo em um ponto com a coordenada y igual a 3/7. — Figura$\PageIndex{8}$

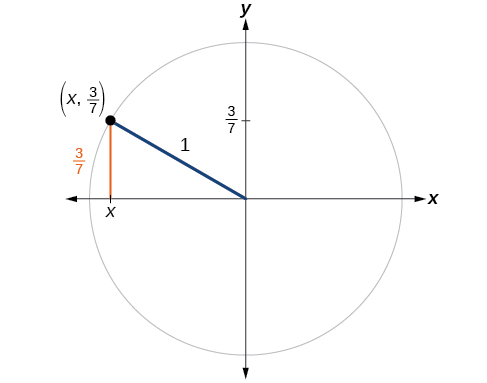
Substituindo o valor conhecido de seno na identidade pitagórica,

\[\begin{align*} \cos ^2 (t)+ \sin ^2(t) &=1 \\ \cos ^2(t)+\dfrac{9}{49} &=1 \\ \cos ^2(t) & = \dfrac{40}{49} \\ \cos (t)=± \sqrt{\dfrac{40}{49}}=±\dfrac{\sqrt{40}}{7}=±\dfrac{2\sqrt{10}}{7} \end{align*}\]

Como o ângulo está no segundo quadrante, sabemos que o valor x é um número real negativo, então o cosseno também é negativo. Então

\[ \cos (t)=−\dfrac{2\sqrt{10}}{7} \nonumber \]

Exercício$\PageIndex{3}$

Se$\cos (t)=\frac{24}{25}$ e tt estiver no quarto quadrante, encontre$ \sin (t)$.

Solução

$\sin (t)=−\frac{7}{25}$

Encontrando senos e cossenos de ângulos especiais

Já aprendemos algumas propriedades dos ângulos especiais, como a conversão de radianos em graus. Também podemos calcular senos e cossenos dos ângulos especiais usando a identidade pitagórica e nosso conhecimento sobre triângulos.

Encontrando senos e cossenos de ângulos de 45°

Primeiro, veremos os ângulos de$45°$ ou$\frac{π}{4}$, conforme mostrado na Figura$\PageIndex{9}$. Um$45°–45°–90°$ triângulo é um triângulo isósceles, então as coordenadas x e y do ponto correspondente no círculo são as mesmas. Como os valores x e y são os mesmos, os valores de seno e cosseno também serão iguais.

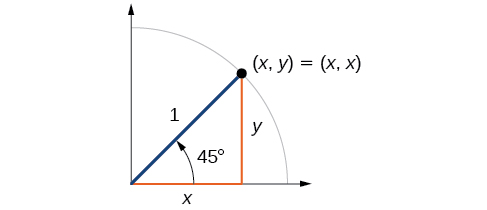
Gráfico de ângulo de 45 graus inscrito em um círculo com raio de 1. Equivalência entre os pontos (x, y) e (x, x) mostrados. — Figura$\PageIndex{9}$

Em$t=\frac{π}{4}$, que é de 45 graus, o raio do círculo unitário divide o primeiro ângulo quadrantal. Isso significa que o raio está ao longo da linha$y=x$. Um círculo unitário tem um raio igual a 1. Então, o triângulo reto formado abaixo da linha$y=x$ tem lados$x$$y (y=x),$ e um raio = 1. Veja a Figura$\PageIndex{10}$.

Gráfico de círculo com ângulo pi/4 inscrito e raio de 1. — Figura$\PageIndex{10}$

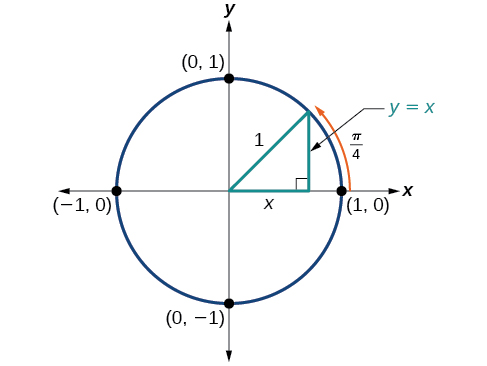
Do Teorema de Pitágoras, obtemos

\[x^2+y^2=1\]

Substituindo$y=x$, obtemos

\[x^2+x^2=1\]

Combinando termos semelhantes que obtemos

\[2x^2=1\]

E resolvendo para$x$, obtemos

\[\begin{align} x^2 &=\dfrac{1}{2} \\ x &=±\dfrac{1}{sqrt{2}} \end{align}\]

No quadrante I,$x=\frac{1}{\sqrt{2}}$.

Em$t=\frac{π}{4}$ ou 45 graus,

\[\begin{align} (x,y) & =(x,x)=(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}) \\ x &= \dfrac{1}{\sqrt{2}},y=\dfrac{1}{\sqrt{2}} \\ \cos t &= \dfrac{1}{\sqrt{2}}, \sin t=\dfrac{1}{\sqrt{2}} \end{align}\]

Se então racionalizarmos os denominadores, obtemos

\[ \begin{align} \cos t &= \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{2}}{\sqrt{2}} \\ &= \dfrac{\sqrt{2}}{2} \\ \sin t &= \dfrac{1}{\sqrt{2}} \dfrac{\sqrt{2}}{\sqrt{2}} \\ &=\dfrac{\sqrt{2}}{2} \end{align}\]

Portanto, as$(x,y)$ coordenadas de um ponto em um círculo de raio$1$ em um ângulo de$45°$ são$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$.

Encontrando senos e cossenos de ângulos de 30° e 60°

Em seguida, encontraremos o cosseno e o seno em um ângulo de$30°$, ou$\frac{π}{6}$. Primeiro, desenharemos um triângulo dentro de um círculo com um lado em um ângulo de$30°$ e outro em um ângulo de$−30°$, conforme mostrado na Figura$\PageIndex{11}$. Se os dois triângulos retos resultantes forem combinados em um triângulo grande, observe que todos os três ângulos desse triângulo maior serão$60°$, conforme mostrado na Figura$\PageIndex{12}$.

Gráfico de um círculo com ângulo de 30 graus e ângulo negativo de 30 graus inscrito para formar um triângulo. — Figura$\PageIndex{11}$

Imagem de dois triângulos 30/60/90 consecutivos. Etiqueta para hipotenusa r e lado y. — Figura$\PageIndex{12}$

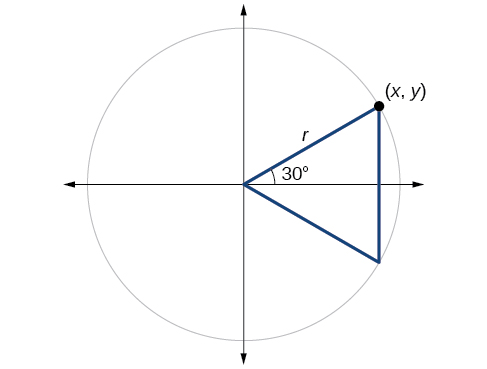
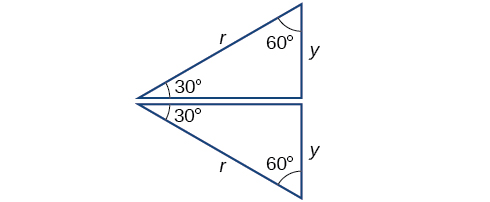
Como todos os ângulos são iguais, os lados também são iguais. A linha vertical tem comprimento e$2y$, como os lados são todos iguais, também podemos concluir que$r=2y$ ou$y=\frac{1}{2}r$. Uma vez que$ \sin t=y$,

\[ \sin (\dfrac{π}{6})=\dfrac{1}{2} \]

E já que$r=1$ em nosso círculo unitário,

\[\begin{align} \sin (\dfrac{π}{6}) & = \dfrac{1}{2}(1) \\ &= \dfrac{1}{2} \end{align}\]

Usando a identidade pitagórica, podemos encontrar o valor do cosseno.

\begin{array}{l} 2 \frac{π}{6} + {pecado}^{2} (\frac{π}{6}) = 1 \\ 2 (\frac{π}{6}) + {(\frac{1}{2})}^{2} = 1 \\ 2 (\frac{π}{6}) = \frac{3}{4} & Use a propriedade raiz quadrada . \\ (\frac{π}{6}) = \frac{\pm \sqrt{3}}{\pm \sqrt{4}} = \frac{\sqrt{3}}{2} & Desde y é positivo, escolha a raiz positiva . \end{array}

As$(x,y)$ coordenadas para o ponto em um círculo de raio$1$ em um ângulo de$30°$ são$(\frac{\sqrt{3}}{2},\frac{1}{2})$. Em$t=\frac{π}{3}$ (60°), o raio do círculo unitário, 1, serve como hipotenusa de um triângulo reto de 30-60-90 graus,$BAD,$ conforme mostrado na Figura$\PageIndex{13}$. $A$O ângulo tem medida de 60°. 60°. No ponto,$B,$ desenhamos um ângulo$ABC$ com a medida de$ 60°$. Sabemos que os ângulos em um triângulo somam$180°$, então a medida do ângulo também$C$ é$60°$. Agora temos um triângulo equilátero. Como cada lado do triângulo equilátero$ABC$ tem o mesmo comprimento e sabemos que um lado é o raio do círculo unitário, todos os lados devem ter comprimento 1.

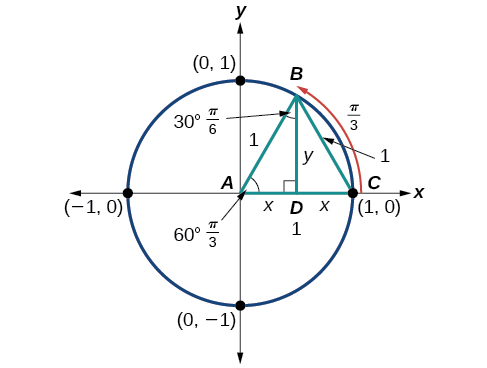
Gráfico de círculo com um triângulo isósceles inscrito que foi dividido ao meio. O triângulo resultante tem um raio de 1 e uma altura de y. Cada uma das duas bases dos triângulos tem um comprimento de x. — Figura$\PageIndex{13}$

A medida do ângulo$ABD$ é de 30°. Então, se for duplo, o ângulo$ABC$ é de 60°. $BD$é a bissetriz perpendicular de$AC$, então ela corta$AC$ ao meio. Isso significa que$AD$ é$12$ o raio, ou$12.$ Observe que$AD$ é a coordenada x do ponto$B$, que está na interseção do ângulo de 60° com o círculo unitário. Isso nos dá um triângulo$BAD$ com hipotenusa de 1 e lado$x$ de comprimento$\frac{1}{2}$.

Do Teorema de Pitágoras, obtemos

\[x^2+y^2=1\]

Substituindo$x=\frac{1}{2}$, obtemos

\[(\dfrac{1}{2})^2+y^2=1\]

Resolvendo para$y$, obtemos

\[\begin{align} \dfrac{1}{4}+y^2 &=1 \\ y^2 &=1−\dfrac{1}{4} \\ y^2 &= \dfrac{3}{4} \\ y &=± \dfrac{\sqrt{3}}{2} \end{align}\]

Como$t=\frac{π}{3}$ tem o lado terminal no quadrante I onde a coordenada y é positiva$y=\frac{\sqrt{3}}{2}$, escolhemos o valor positivo.

Em$t=\frac{π}{3}$ (60°), as$(x,y)$ coordenadas para o ponto em um círculo de raio$1$ em um ângulo de$60°$ são$(\frac{1}{2},\frac{\sqrt{3}}{2})$, então podemos encontrar o seno e o cosseno.

\begin{array}{l} (x, y) = (\frac{1}{2}, \frac{\sqrt{3}}{2}) \\ x = \frac{1}{2}, y = \frac{\sqrt{3}}{2} \\ t = \frac{1}{2}, pecado t = \frac{\sqrt{3}}{2} \end{array}

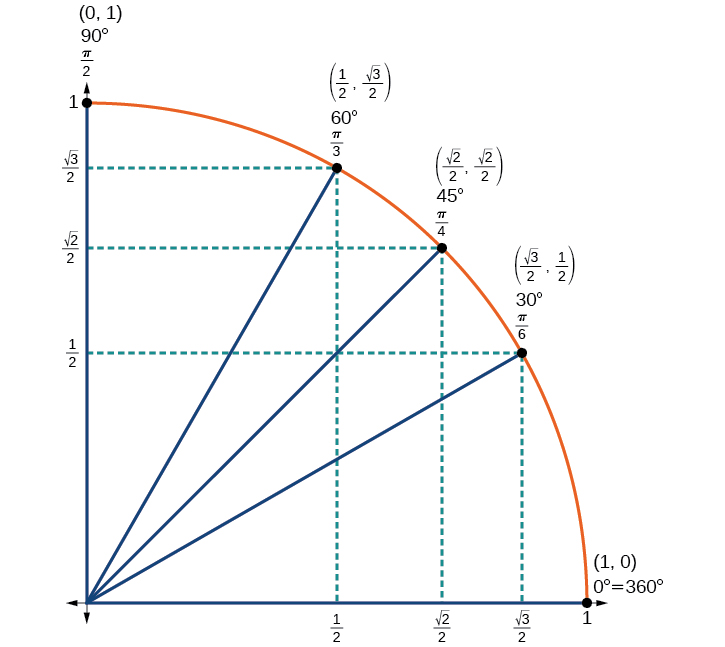
Agora encontramos os valores de cosseno e seno para todos os ângulos mais comumente encontrados no primeiro quadrante do círculo unitário. A tabela$\PageIndex{1}$ resume esses valores.

Tabela$\PageIndex{1}$
Ângulo	0	$\frac{π}{6}$, ou 30	$\frac{π}{4}$, ou 45°	$\frac{π}{3}$, ou 60°	$\frac{π}{2}$, ou 90°
Cosseno	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
Seno	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1

A figura$\PageIndex{14}$ mostra os ângulos comuns no primeiro quadrante do círculo unitário.

Gráfico de um quarto de círculo com ângulos de 0, 30, 45, 60 e 90 graus inscritos. Equivalência de ângulos em radianos mostrada. Os pontos ao longo do círculo estão marcados. — Figura$\PageIndex{14}$

Usando uma calculadora para encontrar seno e cosseno

Para encontrar o cosseno e o seno de ângulos diferentes dos ângulos especiais, recorremos a um computador ou calculadora. Esteja ciente: a maioria das calculadoras pode ser configurada no modo “grau” ou “radiano”, que informa à calculadora as unidades do valor de entrada. Quando avaliamos$ \cos (30)$ em nossa calculadora, ela o avaliará como o cosseno de 30 graus se a calculadora estiver no modo de graus ou o cosseno de 30 radianos se a calculadora estiver no modo radiano.

Como: Dado um ângulo em radianos, use uma calculadora gráfica para encontrar o cosseno

Se a calculadora tiver o modo de graus e o modo radiano, configure-a para o modo radiano.
Pressione a tecla COS.
Insira o valor radiano do ângulo e pressione a tecla de fechar parênteses “)”.
Pressione ENTER.

Exemplo$\PageIndex{4}$: Using a Graphing Calculator to Find Sine and Cosine

Avalie$ \cos (\frac{5π}{3})$ usando uma calculadora gráfica ou um computador.

Solução

Digite as seguintes teclas:

$\mathrm{COS( 5 × π ÷ 3 ) ENTER}$

\[ \cos (\dfrac{5π}{3})=0.5 \nonumber\]

Análise

Podemos encontrar o cosseno ou seno de um ângulo em graus diretamente em uma calculadora com o modo de graus. Para calculadoras ou softwares que usam apenas o modo radiano, podemos encontrar o sinal de$20°$, por exemplo, incluindo o fator de conversão em radianos como parte da entrada:

\[\mathrm{SIN( 20 × π ÷ 180 ) ENTER} \nonumber\]

Exercício$\PageIndex{4}$

Avalie$\sin (\frac{π}{3})$.

Solução

aproximadamente 0,866025403

Identificando o domínio e o intervalo das funções seno e cosseno

Agora que podemos encontrar o seno e o cosseno de um ângulo, precisamos discutir seus domínios e intervalos. Quais são os domínios das funções seno e cosseno? Ou seja, quais são os menores e maiores números que podem ser entradas das funções? Como ângulos menores que 0 e ângulos maiores que 2π 2π ainda podem ser representados graficamente no círculo unitário e têm valores reais de$x, y$$r$, e não há limite inferior ou superior para os ângulos que podem ser inseridos nas funções seno e cosseno. A entrada para as funções seno e cosseno é a rotação do eixo x positivo, e isso pode ser qualquer número real.

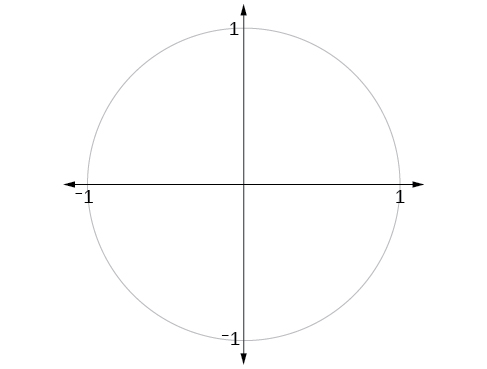
Quais são os intervalos das funções seno e cosseno? Quais são os menores e maiores valores possíveis para sua produção? Podemos ver as respostas examinando o círculo unitário, conforme mostrado na Figura$\PageIndex{15}$. Os limites da coordenada x são$ [−1,1]$. Os limites da coordenada y também são$[−1,1]$. Portanto, o alcance das funções seno e cosseno é$[−1,1]$.

Gráfico do círculo unitário. — Figura$\PageIndex{15}$

Encontrando ângulos de referência

Discutimos como encontrar o seno e o cosseno para ângulos no primeiro quadrante, mas e se nosso ângulo estiver em outro quadrante? Para qualquer ângulo dado no primeiro quadrante, há um ângulo no segundo quadrante com o mesmo valor senoidal. Como o valor do seno é a coordenada y no círculo unitário, o outro ângulo com o mesmo seno compartilhará o mesmo valor y, mas terá o valor x oposto. Portanto, seu valor de cosseno será o oposto do valor do cosseno do primeiro ângulo.

Da mesma forma, haverá um ângulo no quarto quadrante com o mesmo cosseno do ângulo original. O ângulo com o mesmo cosseno compartilhará o mesmo valor x, mas terá o valor y oposto. Portanto, seu valor senoidal será o oposto do valor seno do ângulo original.

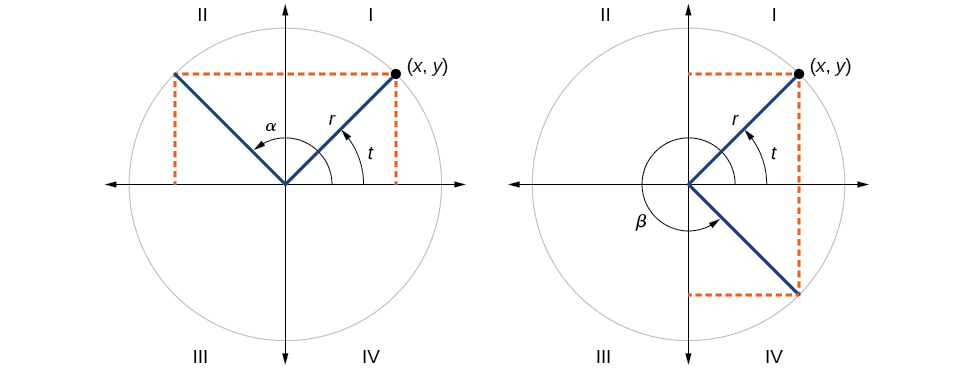
Conforme mostrado na Figura$\PageIndex{16}$, o ângulo$α$ tem o mesmo valor senoidal do ângulo$t$; os valores do cosseno são opostos. O ângulo$β$ tem o mesmo valor de cosseno que o ângulo$t$; os valores do seno são opostos.

\begin{array}{l} pecado (t) = pecado (α) & e & (t) = - (α) \\ pecado (t) = - pecado (β) & e & (t) = (β) \end{array}

Gráfico de dois círculos lado a lado. O primeiro gráfico tem círculo com ângulo t e ângulo alfa com raio r. Ângulo t tem seu lado terminal no Quadrante I, enquanto o ângulo alfa tem seu lado terminal no Quadrante II. O segundo gráfico tem círculo com ângulo t e ângulo beta inscrito com raio r. O ângulo t tem seu lado terminal no Quadrante I, enquanto o ângulo beta tem seu lado terminal no Quadrante IV. — Figura$\PageIndex{16}$

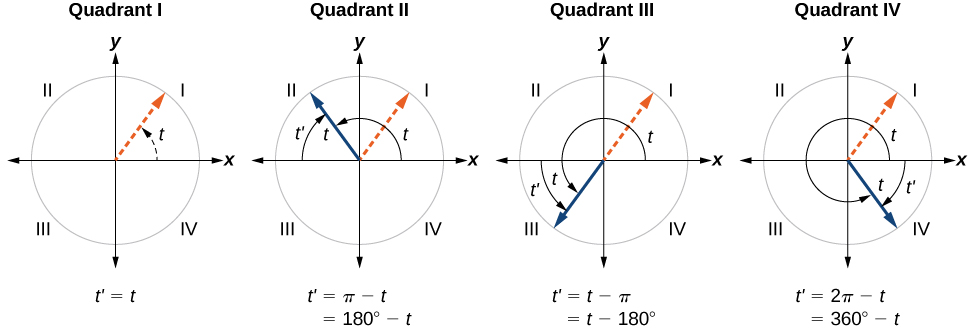
Lembre-se de que o ângulo de referência de um ângulo é o ângulo agudo$t$, formado pelo lado terminal do ângulo$t$ e pelo eixo horizontal. Um ângulo de referência é sempre um ângulo entre$0$ e$90°$, ou$0$ e$\frac{π}{2}$ radianos. Como podemos ver na Figura$\PageIndex{17}$, para qualquer ângulo nos quadrantes II, III ou IV, há um ângulo de referência no quadrante I.

Quatro gráficos lado a lado. O primeiro gráfico mostra um ângulo de t no quadrante 1 em sua posição normal. O segundo gráfico mostra um ângulo de t no quadrante 2 devido a uma rotação de pi menos t. O terceiro gráfico mostra um ângulo de t no quadrante 3 devido a uma rotação de t menos pi. O quarto gráfico mostra um ângulo de t no quadrante 4 devido a uma rotação de dois pi menos t. — Figura$\PageIndex{17}$

como: Dado um ângulo entre$0$ and $2π$, find its reference angle

Um ângulo no primeiro quadrante é seu próprio ângulo de referência.
Para um ângulo no segundo ou terceiro quadrante, o ângulo de referência é$|π−t|$ ou$|180°−t|$.
Para um ângulo no quarto quadrante, o ângulo de referência é$2π−t$ ou$360°−t.$
Se um ângulo for menor$0$ ou maior,$2π,$ adicione ou subtraia$2π$ quantas vezes forem necessárias para encontrar um ângulo equivalente entre$0$$2π$ e.

Exemplo$\PageIndex{5}$: Finding a Reference Angle

Encontre o ângulo de referência de$225°$ conforme mostrado na Figura$\PageIndex{18}$.

Gráfico de círculo com ângulo de 225 graus inscrito. — Figura$\PageIndex{18}$

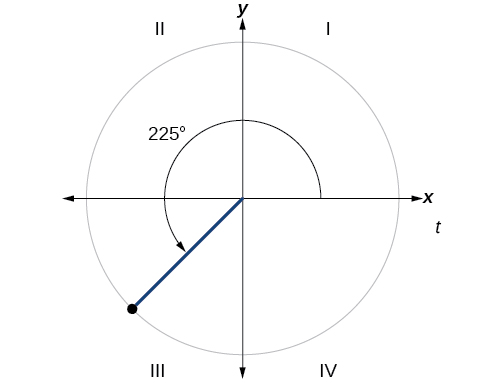
Solução

Como$ 225°$ está no terceiro quadrante, o ângulo de referência é

\[|(180°−225°)|=|−45°|=45°\]

Exercício$\PageIndex{5}$:

Encontre o ângulo de referência de$\frac{5π}{3}$.

Solução

$\frac{π}{3}$

Usando ângulos de referência

Agora, vamos reconsiderar a roda gigante apresentada no início desta seção. Suponha que um passageiro tire uma foto enquanto está parado a vinte pés acima do nível do solo. O piloto então gira três quartos do círculo. Qual é a nova elevação do ciclista? Para responder perguntas como essa, precisamos avaliar as funções seno ou cosseno em ângulos maiores que 90 graus ou em um ângulo negativo. Os ângulos de referência permitem avaliar funções trigonométricas para ângulos fora do primeiro quadrante. Eles também podem ser usados para encontrar$(x,y)$ coordenadas para esses ângulos. Usaremos o ângulo de referência do ângulo de rotação combinado com o quadrante em que se encontra o lado terminal do ângulo.

Usando ângulos de referência para avaliar funções trigonométricas

Podemos encontrar o cosseno e o seno de qualquer ângulo em qualquer quadrante se soubermos o cosseno ou seno de seu ângulo de referência. Os valores absolutos do cosseno e do seno de um ângulo são os mesmos do ângulo de referência. O sinal depende do quadrante do ângulo original. O cosseno será positivo ou negativo, dependendo do sinal dos valores de x nesse quadrante. O seno será positivo ou negativo, dependendo do sinal dos valores de y nesse quadrante.

USANDO ÂNGULOS DE REFERÊNCIA PARA ENCONTRAR COSSENO E SENO

Os ângulos têm cossenos e senos com o mesmo valor absoluto dos cossenos e senos de seus ângulos de referência. O sinal (positivo ou negativo) pode ser determinado a partir do quadrante do ângulo.

como: Dado um ângulo na posição padrão, encontre o ângulo de referência e o cosseno e o seno do ângulo original

Meça o ângulo entre o lado terminal do ângulo dado e o eixo horizontal. Esse é o ângulo de referência.
Determine os valores do cosseno e do seno do ângulo de referência.
Dê ao cosseno o mesmo sinal dos valores de x no quadrante do ângulo original.
Dê ao seno o mesmo sinal dos valores de y no quadrante do ângulo original.

Exemplo$\PageIndex{6}$: Using Reference Angles to Find Sine and Cosine

Usando um ângulo de referência, encontre o valor exato de$\cos (150°)$$ \sin (150°)$ e.
Usando o ângulo de referência, encontre$ \cos \frac{5π}{4}$$\sin \frac{5π}{4}$ e.

Solução

Isso nos diz que 150° tem os mesmos valores de seno e cosseno de 30°, exceto pelo sinal. Nós sabemos disso

Como 150° está no segundo quadrante, a coordenada x do ponto no círculo é negativa, então o valor do cosseno é negativo. A coordenada y é positiva, então o valor do seno é positivo. $(150°) = - \frac{\sqrt{3}}{2} e pecado (150°) = \frac{1}{2}$
$\frac{5π}{4}$está no terceiro quadrante. Seu ângulo de referência é$\frac{5π}{4}−π=\frac{π}{4}$. O cosseno e o seno de$\frac{π}{4}$ são ambos$\frac{sqrt{2}}{2}$. No terceiro quadrante, x x e y y são negativos, então:
\[\cos \dfrac{5π}{4}=−\dfrac{\sqrt{2}}{2} \;\; \text{and} \; \; \sin \dfrac{5π}{4}=−\dfrac{\sqrt{2}}{2}\]

Exercício$\PageIndex{6}$

Use o ângulo de referência de$315°$ para encontrar$ \cos (315°) $$\sin (315°)$ e.
Use o ângulo de referência de$−\frac{π}{6}$ para encontrar$ \cos (−\frac{π}{6})$$ \sin (−\frac{π}{6})$ e.

Solução

$ \cos (315°)= \frac{\sqrt{2}}{2}, \sin (315°)=\frac{–\sqrt{2}}{2}$

$\cos (−\frac{π}{6})=\frac{\sqrt{3}}{2}, \sin (−\frac{π}{6})=−\frac{1}{2} $

Usando ângulos de referência para encontrar coordenadas

Agora que aprendemos como encontrar os valores de cosseno e seno para ângulos especiais no primeiro quadrante, podemos usar simetria e ângulos de referência para preencher os valores de cosseno e seno para o resto dos ângulos especiais no círculo unitário. Eles são mostrados na Figura$\PageIndex{19}$. Reserve um tempo para aprender as$(x,y)$ coordenadas de todos os ângulos principais no primeiro quadrante.

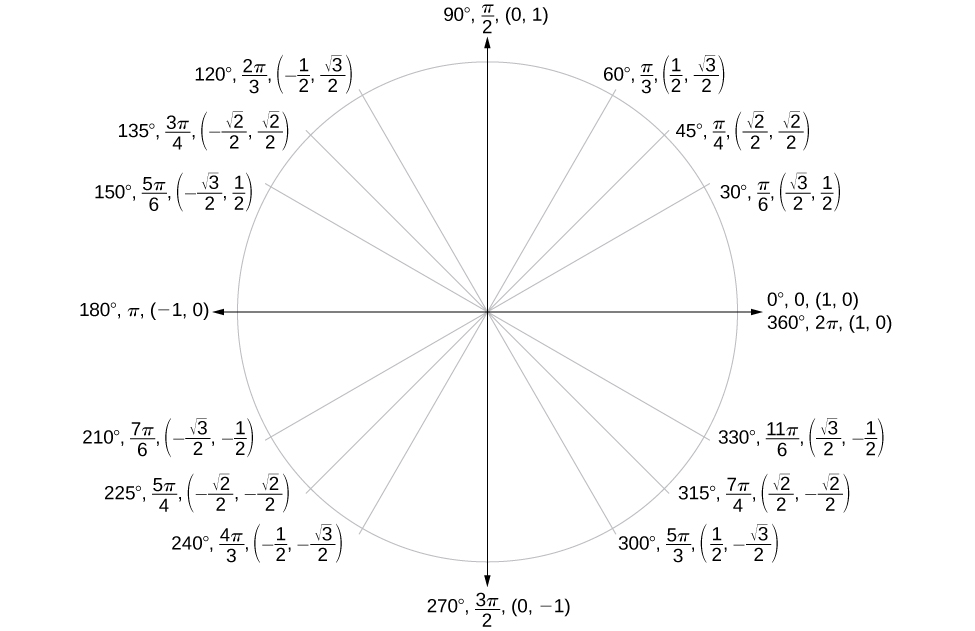
Gráfico do círculo unitário com ângulos em graus, ângulos em radianos e pontos ao longo do círculo inscrito. — Figura$\PageIndex{19}$: Ângulos e coordenadas especiais dos pontos correspondentes no círculo unitário

Além de aprender os valores para ângulos especiais, podemos usar ângulos de referência para encontrar$(x,y)$ coordenadas de qualquer ponto no círculo unitário, usando o que sabemos sobre ângulos de referência junto com as identidades

\[\begin{align*} x &= \cos t \\ y & = \sin t \end{align*}\]

Primeiro, encontramos o ângulo de referência correspondente ao ângulo dado. Em seguida, pegamos os valores de seno e cosseno do ângulo de referência e damos a eles os sinais correspondentes aos valores y e x do quadrante.

como: Dado o ângulo de um ponto em um círculo e o raio do círculo, encontre o$(x,y)$ coordinates of the point

Encontre o ângulo de referência medindo o menor ângulo em relação ao eixo x.
Encontre o cosseno e o seno do ângulo de referência.
Determine os sinais apropriados para$x$ e$y$ no quadrante fornecido.

Exemplo$\PageIndex{7}$: Using the Unit Circle to Find Coordinates

Encontre as coordenadas do ponto no círculo unitário em um ângulo de$\frac{7π}{6}$.

Solução

Sabemos que o ângulo$\frac{7π}{6}$ está no terceiro quadrante.

Primeiro, vamos encontrar o ângulo de referência medindo o ângulo em relação ao eixo x. Para encontrar o ângulo de referência de um ângulo cujo lado terminal está no quadrante III, encontramos a diferença do ângulo e π. π.

\[\dfrac{7π}{6}−π=\dfrac{π}{6}\]

A seguir, encontraremos o cosseno e o seno do ângulo de referência:

\[\cos (\dfrac{π}{6})=\dfrac{3}{2} \;\; \sin (\dfrac{π}{6})=\dfrac{1}{2}\]

Devemos determinar os sinais apropriados para x e y em um determinado quadrante. Como nosso ângulo original está no terceiro quadrante, onde x x e y y são negativos, tanto o cosseno quanto o seno são negativos.

\[\begin{align} \cos (\dfrac{7π}{6}) &=−\dfrac{\sqrt{3}}{2} \\ \sin (\dfrac{7π}{6}) & =−\dfrac{1}{2} \end{align}\]

Agora podemos calcular as$(x,y)$ coordenadas usando as identidades$x= \cos θ$$y= \sin θ$ e.

As coordenadas do ponto estão$(−\frac{\sqrt{3}}{2},−\frac{1}{2})$ no círculo unitário.

Exercício$\PageIndex{7}$:

Encontre as coordenadas do ponto no círculo unitário em um ângulo de$\frac{5π}{3}$.

Solução

$(\frac{1}{2},−\frac{\sqrt{3}}{2})$

meios de comunicação

Acesse esses recursos on-line para obter instruções e práticas adicionais com as funções seno e cosseno.

Equações-chave

Cosseno	$ \cos t=x$
Seno	$ \sin t=y$
Identidade pitagórica	$ \cos ^2 t+ \sin ^2 t=1$

Conceitos-chave

Encontrar os valores da função para o seno e o cosseno começa com o desenho de um círculo unitário, que está centrado na origem e tem um raio de 1 unidade.
Usando o círculo unitário, o seno de um ângulo$t$ é igual ao valor y do ponto final no círculo unitário de um arco de comprimento,$t$ enquanto o cosseno de um ângulo$t$ é igual ao valor x do ponto final. Veja o exemplo.
Os valores de seno e cosseno são determinados mais diretamente quando o ponto correspondente no círculo unitário cai em um eixo. Veja o exemplo.
Quando o seno ou cosseno é conhecido, podemos usar a identidade pitagórica para encontrar o outro. A identidade pitagórica também é útil para determinar os senos e cossenos de ângulos especiais. Veja o exemplo.
Calculadoras e softwares gráficos são úteis para encontrar senos e cossenos se o procedimento adequado para inserir informações for conhecido. Veja o exemplo.
O domínio das funções seno e cosseno são todos números reais.
O alcance das funções seno e cosseno é$[−1,1]$.
O seno e o cosseno de um ângulo têm o mesmo valor absoluto que o seno e o cosseno de seu ângulo de referência.
Os sinais do seno e do cosseno são determinados a partir dos valores x e y no quadrante do ângulo original.
O ângulo de referência de um ângulo é o ângulo de tamanho$t$, formado pelo lado terminal do ângulo$t$ e pelo eixo horizontal. Veja o exemplo.
Os ângulos de referência podem ser usados para encontrar o seno e o cosseno do ângulo original. Veja o exemplo.
Os ângulos de referência também podem ser usados para encontrar as coordenadas de um ponto em um círculo. Veja o exemplo.

Glossário

função cosseno: o valor x do ponto em um círculo unitário correspondente a um determinado ângulo

Identidade pitagórica: um corolário do Teorema de Pitágoras afirmando que o quadrado do cosseno de um determinado ângulo mais o quadrado do seno desse ângulo é igual a 1

função senoidal: o valor y do ponto em um círculo unitário correspondente a um determinado ângulo

círculo unitário: um círculo com um centro em$(0,0)$ e raio 1.

Ângulo	0	\(\frac{π}{6}\), ou 30	\(\frac{π}{4}\), ou 45°	\(\frac{π}{3}\), ou 60°	\(\frac{π}{2}\), ou 90°
Cosseno	1	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{1}{2}\)	0
Seno	0	\(\frac{1}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{3}}{2}\)	1

Cosseno	\( \cos t=x\)
Seno	\( \sin t=y\)
Identidade pitagórica	\( \cos ^2 t+ \sin ^2 t=1\)