13.1: Ângulos
- Page ID
- 189246
Objetivos de
- Desenhe ângulos na posição padrão.
- Converta entre graus e radianos.
- Encontre ângulos coterminais.
- Encontre o comprimento de um arco circular.
- Use a velocidade linear e angular para descrever o movimento em um caminho circular.
Um jogador de golfe balança para bater uma bola sobre uma armadilha de areia e para o green. Um piloto de avião manobra um avião em direção a uma pista estreita. Um estilista cria a última moda. O que todos eles têm em comum? Todos eles trabalham com ângulos, assim como todos nós em um momento ou outro. Às vezes, precisamos medir ângulos exatamente com instrumentos. Outras vezes, nós os estimamos ou os julgamos a olho nu. De qualquer forma, o ângulo adequado pode fazer a diferença entre o sucesso e o fracasso em muitos empreendimentos. Nesta seção, examinaremos as propriedades dos ângulos.
Desenhando ângulos na posição padrão
Definir corretamente um ângulo primeiro requer que definamos um raio. Um raio consiste em um ponto em uma linha e todos os pontos que se estendem em uma direção a partir desse ponto. O primeiro ponto é chamado de ponto final do raio. Podemos nos referir a um raio específico declarando seu ponto final e qualquer outro ponto nele. O raio na Figura\(\PageIndex{1}\) pode ser denominado raio EF ou em forma de símbolo\(\overrightarrow{EF}\).
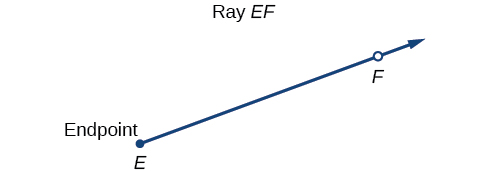
Um ângulo é a união de dois raios com um ponto final comum. O ponto final é chamado de vértice do ângulo e os dois raios são os lados do ângulo. O ângulo na Figura\(\PageIndex{2}\) é formado a partir de\(\overrightarrow{ED}\)\(\overrightarrow{EF}\) e. Os ângulos podem ser nomeados usando um ponto em cada raio e vértice, como ângulo DEF, ou em forma de símbolo\(∠DEF.\)
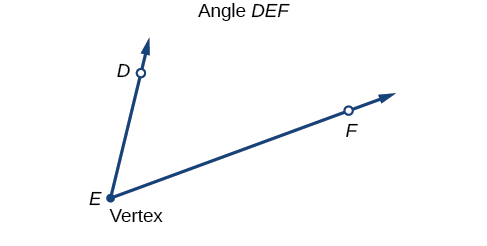
As letras gregas são frequentemente usadas como variáveis para a medida de um ângulo. A tabela\(\PageIndex{1}\) é uma lista de letras gregas comumente usadas para representar ângulos, e um ângulo de amostra é mostrado na Figura\(\PageIndex{3}\).
| \(θ\) | \(φ \text{ or }ϕ\) | \(α\) | \(β\) | \(γ\) |
| teta | phi | alfa | beta | gama |
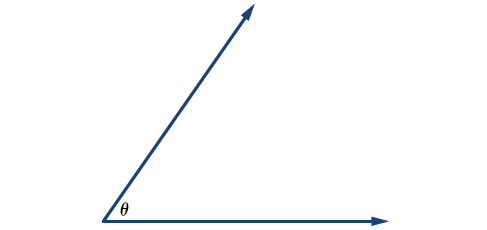
Figura \(\PageIndex{3}\): Ângulo teta, mostrado como\(∠θ\)
A criação de ângulos é um processo dinâmico. Começamos com dois raios deitados um sobre o outro. Deixamos um fixo no lugar e giramos o outro. O raio fixo é o lado inicial e o raio girado é o lado terminal. Para identificar os diferentes lados, indicamos a rotação com um pequeno arco e seta próximos ao vértice, como na Figura\(\PageIndex{4}\).
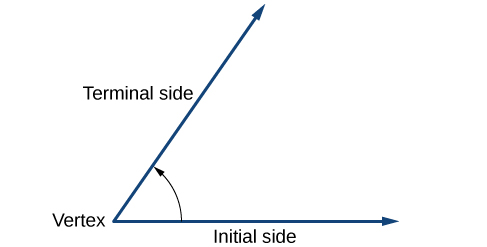
Conforme discutimos no início da seção, existem muitas aplicações para ângulos, mas para usá-los corretamente, precisamos ser capazes de medi-los. A medida de um ângulo é a quantidade de rotação do lado inicial para o lado terminal. Provavelmente, a unidade de medição de ângulo mais conhecida é o grau. Um grau é\(\frac{1}{360}\) de rotação circular, então uma rotação circular completa contém 360 graus. Um ângulo medido em graus deve sempre incluir a unidade “graus” após o número ou incluir o símbolo de grau°. Por exemplo, 90 graus = 90°.
Para formalizar nosso trabalho, começaremos desenhando ângulos em um plano de coordenadas x - y. Os ângulos podem ocorrer em qualquer posição no plano coordenado, mas para fins de comparação, a convenção é ilustrá-los na mesma posição sempre que possível. Um ângulo está na posição padrão se seu vértice estiver localizado na origem e seu lado inicial se estender ao longo do eixo x positivo. Veja a Figura\(\PageIndex{5}\).
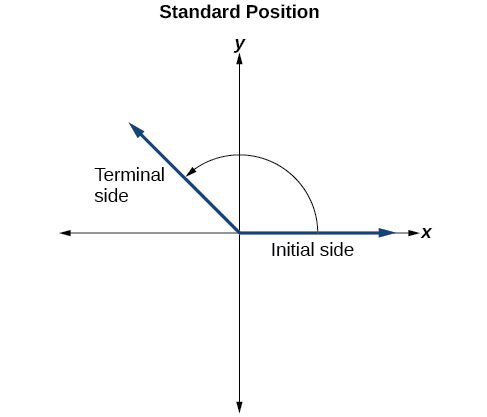
Se o ângulo for medido no sentido anti-horário do lado inicial para o lado terminal, o ângulo é considerado um ângulo positivo. Se o ângulo for medido no sentido horário, diz-se que o ângulo é negativo.
Desenhar um ângulo na posição padrão sempre começa da mesma maneira — desenhe o lado inicial ao longo do eixo x positivo. Para colocar o lado terminal do ângulo, devemos calcular a fração de uma rotação completa que o ângulo representa. Fazemos isso dividindo a medida do ângulo em graus por 360°. Por exemplo, para desenhar um ângulo de 90°, calculamos isso\(\frac{90°}{360°}=\frac{1}{4}\). Portanto, o lado do terminal estará a um quarto do círculo, movendo-se no sentido anti-horário a partir do eixo x positivo. Para desenhar um ângulo de 360°, calculamos isso\(\frac{360°}{360°}=1\). Portanto, o lado do terminal será 1 rotação completa ao redor do círculo, movendo-se no sentido anti-horário a partir do eixo x positivo. Nesse caso, o lado inicial e o lado terminal se sobrepõem. Veja a Figura\(\PageIndex{6}\).
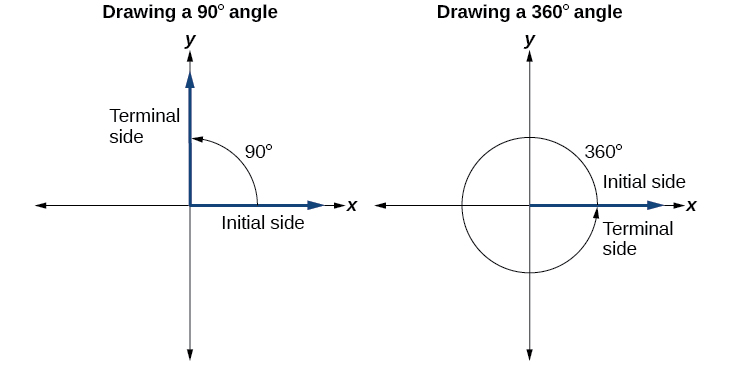
Como definimos um ângulo na posição padrão pelo lado inicial, temos um tipo especial de ângulo cujo lado terminal está em um eixo, um ângulo quadrantal. Esse tipo de ângulo pode ter uma medida de 0°, 90°, 180°, 270° ou 360°. Veja a Figura\(\PageIndex{7}\).
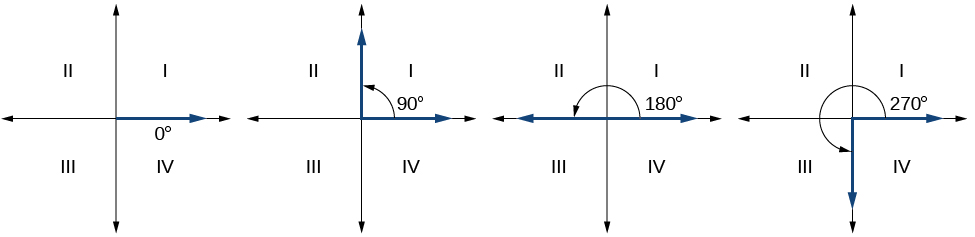
ÂNGULOS QUADRANTAIS
Ângulos quadrantais são ângulos na posição padrão cujo lado terminal está em um eixo, incluindo 0°, 90°, 180°, 270° ou 360°.
Dada a medida do ângulo em graus, desenhe o ângulo na posição padrão
- Expresse a medida do ângulo como uma fração de 360°.
- Reduza a fração para a forma mais simples.
- Desenhe um ângulo que contenha a mesma fração do círculo, começando no eixo x positivo e movendo-se no sentido anti-horário para ângulos positivos e no sentido horário para ângulos negativos.
Exemplo\(\PageIndex{1}\): Drawing an Angle in Standard Position Measured in Degrees
- Desenhe um ângulo de 30° na posição padrão.
- Desenhe um ângulo de −135° na posição padrão.
Solução
- Divida a medida do ângulo em 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]
Para reescrever a fração em uma fração mais familiar, podemos reconhecer que
\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]
Um duodécimo é igual a um terço de um quarto, portanto, dividindo um quarto de rotação em terços, podemos esboçar uma linha a 30°, como na Figura\(\PageIndex{8}\).
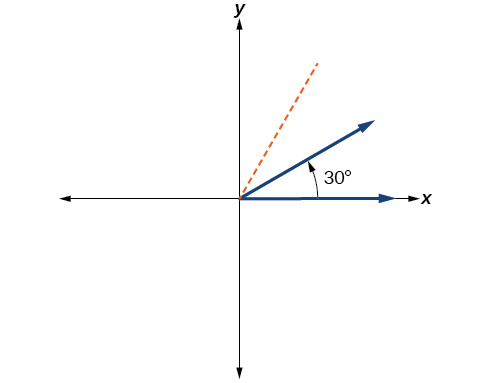
Figura\(\PageIndex{8}\) - Divida a medida do ângulo em 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]
Nesse caso, podemos reconhecer que
\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]
Menos três oitavos é uma vez e meia por quarto, então colocamos uma linha movendo-se no sentido horário um quarto inteiro e metade de outro quarto, como na Figura\(\PageIndex{9}\).
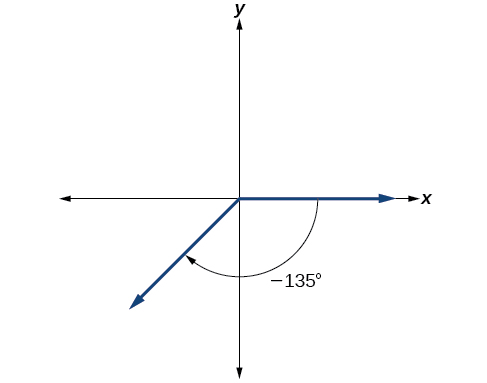
Figura\(\PageIndex{9}\)
\(\PageIndex{1}\):
Mostre um ângulo de 240° em um círculo na posição padrão.
Solução
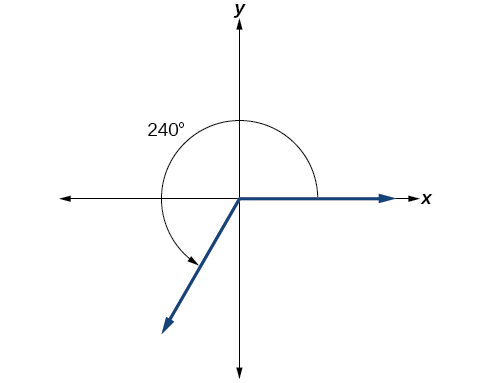
Conversão entre graus e radianos
Dividir um círculo em 360 partes é uma escolha arbitrária, embora crie a conhecida medição de graus. Podemos escolher outras formas de dividir um círculo. Para encontrar outra unidade, pense no processo de desenhar um círculo. Imagine que você pare antes que o círculo seja concluído. A parte que você desenhou é chamada de arco. Um arco pode ser uma parte de um círculo completo, um círculo completo ou mais de um círculo completo, representado por mais de uma rotação completa. O comprimento do arco ao redor de um círculo inteiro é chamado de circunferência desse círculo.
A circunferência de um círculo é\(C=2πr\). Se dividirmos os dois lados dessa equação por\(r\), criaremos a razão entre a circunferência e o raio, que é sempre\(2π\) independente do comprimento do raio. Portanto, a circunferência de qualquer círculo é\(2π≈6.28\) vezes o comprimento do raio. Isso significa que se pegássemos uma corda do tamanho do raio e a usássemos para medir comprimentos consecutivos ao redor da circunferência, haveria espaço para seis cordas completas e pouco mais de um quarto de sétimo, conforme mostrado na Figura\(\PageIndex{11}\).
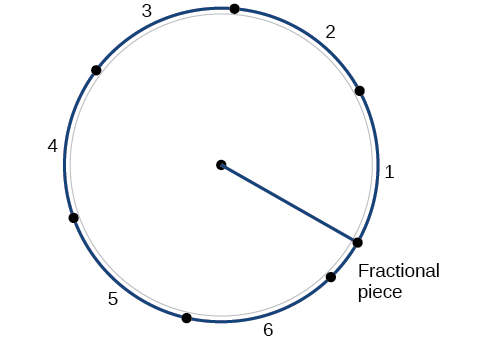
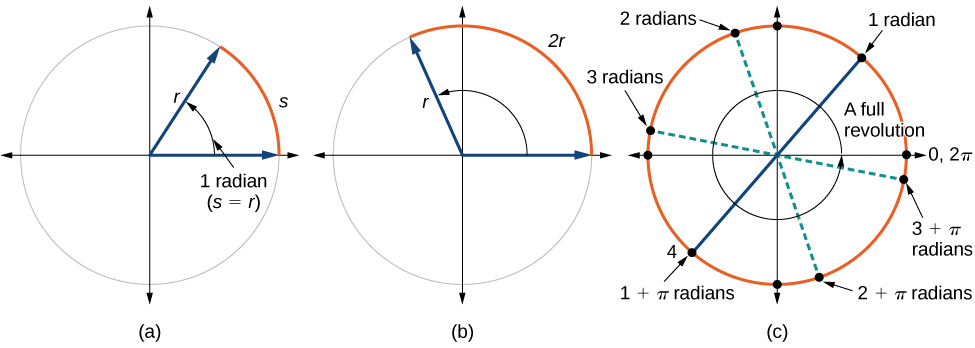
Isso nos leva à nossa nova medida de ângulo. Um radiano é a medida de um ângulo central de um círculo que intercepta um arco de comprimento igual ao raio desse círculo. Um ângulo central é um ângulo formado no centro de um círculo por dois raios. Como a circunferência total é igual a\(2π\) vezes o raio, uma rotação circular completa é\(2π\) radianos. Então
\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]
Veja a Figura\(\PageIndex{12}\). Observe que quando um ângulo é descrito sem uma unidade específica, ele se refere à medida em radianos. Por exemplo, uma medida de ângulo de 3 indica 3 radianos. Na verdade, a medida em radianos é adimensional, pois é o quociente de um comprimento (circunferência) dividido por um comprimento (raio) e as unidades de comprimento são canceladas.
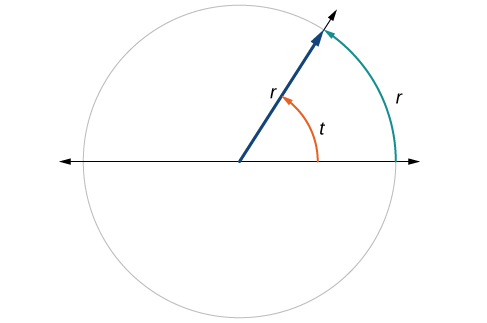
Relacionando comprimentos de arcos com raio
O comprimento do arco\(s\) é o comprimento da curva ao longo do arco. Assim como a circunferência total de um círculo sempre tem uma relação constante com o raio, o comprimento do arco produzido por qualquer ângulo também tem uma relação constante com o raio, independentemente do comprimento do raio.
Essa proporção, chamada de medida em radianos, é a mesma, independentemente do raio do círculo — depende somente do ângulo. Essa propriedade nos permite definir uma medida de qualquer ângulo como a razão entre o comprimento do arco s s e o raio\(r\). Veja a Figura\(\PageIndex{13}\).
\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]
Se\( s=r\), então\(θ=\frac{r}{r}= 1 \text{ radian.}\)
Para elaborar essa ideia, considere dois círculos, um com raio 2 e outro com raio 3. Lembre-se de que a circunferência de um círculo é\(C=2πr\), onde\(r\) está o raio. O círculo menor então tem circunferência\(2π(2)=4π\) e o maior tem circunferência\(2π(3)=6π\). Agora desenhamos um ângulo de 45° nos dois círculos, como na Figura\(\PageIndex{14}\).
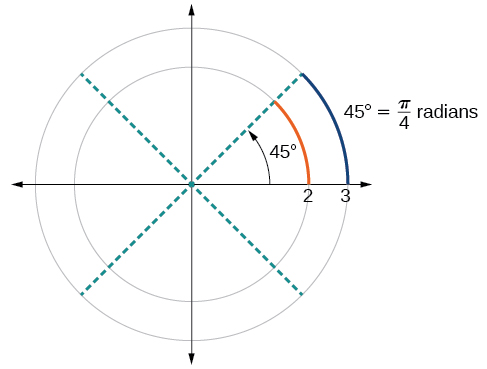
Observe o que acontece se encontrarmos a proporção do comprimento do arco dividida pelo raio da circunferência.
\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]
Como ambas as proporções são\(\frac{1}{4}π\), as medidas angulares de ambos os círculos são as mesmas, mesmo que o comprimento e o raio do arco sejam diferentes.
RADIANOS
Um radiano é a medida do ângulo central de um círculo de forma que o comprimento do arco entre o lado inicial e o lado terminal seja igual ao raio do círculo. Uma revolução completa (360°) é igual a\(2\pi\) radianos. Uma meia revolução (180°) é equivalente a\(\pi\) radianos.
A medida radiana de um ângulo é a razão entre o comprimento do arco subtendido pelo ângulo e o raio do círculo. Em outras palavras, se\(s\) é o comprimento de um arco de um círculo e\(r\) é o raio do círculo, então o ângulo central que contém esse arco mede\(\frac{s}{r}\) os radianos. Em um círculo de raio 1, a medida em radianos corresponde ao comprimento do arco.
Uma medida de 1 radiano parece ser de cerca de 60°. Isso está correto?
Sim. É aproximadamente 57,3°. Como \(2π\)os radianos são iguais a 360°, os\(1\) radianos são iguais\(\frac{360°}{2π}≈57.3°\).
Usando radianos
Como a medida em radianos é a proporção de dois comprimentos, é uma medida sem unidade. Por exemplo, na Figura\(\PageIndex{14}\), suponha que o raio fosse de 2 polegadas e a distância ao longo do arco também fosse de 2 polegadas. Quando calculamos a medida radiana do ângulo, as “polegadas” são canceladas e temos um resultado sem unidades. Portanto, não é necessário escrever o rótulo “radianos” após uma medida em radianos e, se virmos um ângulo que não esteja rotulado com “graus” ou com o símbolo do grau, podemos assumir que é uma medida em radianos.
Considerando o caso mais básico, o círculo unitário (um círculo com raio 1), sabemos que 1 rotação é igual a 360 graus, 360°. Também podemos rastrear uma rotação em torno de um círculo encontrando a circunferência\(C=2πr\),, e para o círculo unitário.\(C=2π.\) Essas duas maneiras diferentes de girar em torno de um círculo nos permitem converter graus em radianos.
\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]
Identificação de ângulos especiais medidos em radianos
Além de conhecer as medidas em graus e radianos de um quarto de revolução, meia revolução e revolução completa, existem outros ângulos frequentemente encontrados em uma revolução de um círculo com os quais devemos estar familiarizados. É comum encontrar múltiplos de 30, 45, 60 e 90 graus. Esses valores são mostrados na Figura\(\PageIndex{15}\). Memorizar esses ângulos será muito útil à medida que estudamos as propriedades associadas aos ângulos.
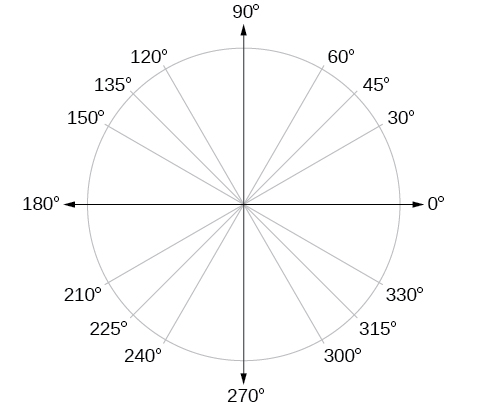
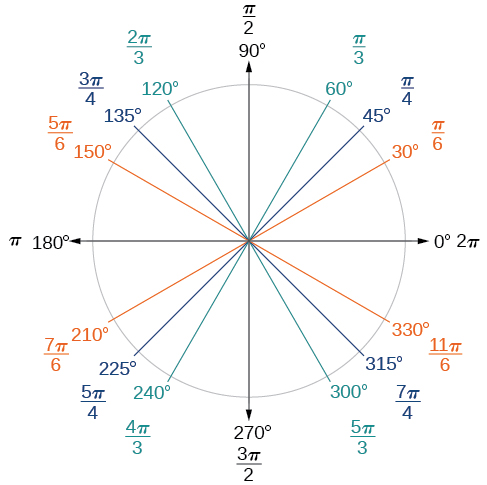
Agora, podemos listar os valores radianos correspondentes para as medidas comuns de um círculo correspondentes às listadas na Figura\(\PageIndex{15}\), que são mostradas na Figura\(\PageIndex{16}\). Certifique-se de que você pode verificar cada uma dessas medidas.
Exemplo\(\PageIndex{2}\): Finding a Radian Measure
Encontre a medida radiana de um terço de uma rotação completa.
Solução
Para qualquer círculo, o comprimento do arco ao longo dessa rotação seria um terço da circunferência. Nós sabemos disso
\[1 \text{ rotation}=2πr\]
Então,
\[\begin{align}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \end{align}\]
A medida em radianos seria o comprimento do arco dividido pelo raio.
\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]
\(\PageIndex{2}\)
Encontre a medida radiana de três quartos de uma rotação completa.
Solução
\[\dfrac{3π}{2}\]
Conversão entre radianos e graus
Como graus e radianos medem ângulos, precisamos ser capazes de converter entre eles. Podemos fazer isso facilmente usando uma proporção.
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Essa proporção mostra que a medida do ângulo\(θ\) em graus dividida por 180 é igual à medida do ângulo\(θ\) em radianos dividida por\(π.\) Ou, formulada de outra forma, graus é igual a 180, assim como radianos\(π\).
\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]
CONVERSÃO ENTRE RADIANOS E GRAUS
Para converter entre graus e radianos, use a proporção
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Exemplo\(\PageIndex{3}\): Converting Radians to Degrees
Converta cada medida radiana em graus.
- \(\frac{π}{6}\)
- 3
Solução
Como recebemos radianos e queremos graus, devemos estabelecer uma proporção e resolvê-la.
- Usamos a proporção, substituindo as informações fornecidas.
\[\begin{align}\dfrac{θ}{180} &=\dfrac{θ^R}{π} \\[2mm] \dfrac{θ}{180} & =\dfrac{\frac{π}{6}}{π} \\ θ & =\dfrac{180}{6} \\ θ & =30^∘ \end{align}\]
- Usamos a proporção, substituindo as informações fornecidas.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{θ}{180} &=\dfrac{3}{π} \\ θ &= \dfrac{3(180)}{π} \\ θ & ≈172^∘ \end{align}\]
\(\PageIndex{3}\)
Converta\(−\frac{3π}{4}\) radianos em graus.
Solução
−135°
Exemplo\(\PageIndex{4}\): Converting Degrees to Radians
Converta\(15\) graus em radianos.
Solução
Neste exemplo, começamos com graus e queremos radianos, então novamente configuramos uma proporção e a resolvemos, mas substituímos as informações fornecidas em uma parte diferente da proporção.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{15}{180} &=\dfrac{θ^R}{π} \\ \dfrac{15π}{180} & =θ^R \\ \dfrac{π}{12} & =θ^R \end{align}\]
Análise
Outra forma de pensar sobre esse problema é lembrando disso\(30^∘=\frac{π}{6}\). Porque\(15^∘=\frac{1}{2}(30^∘)\), podemos descobrir que\(\frac{1}{2}(\frac{π}{6})\) é\(\frac{π}{12}\).
\(\PageIndex{4}\)
Converta 126° em radianos.
Solução
\(\frac{7π}{10}\)
Encontrando ângulos coterminais
A conversão entre graus e radianos pode facilitar o trabalho com ângulos em algumas aplicações. Para outros aplicativos, talvez precisemos de outro tipo de conversão. É mais difícil trabalhar com ângulos negativos e ângulos maiores que uma rotação completa do que aqueles na faixa de 0° a 360° ou 0\(2π\) a. Seria conveniente substituir esses ângulos fora de alcance por um ângulo correspondente dentro do alcance de uma única revolução.
É possível que mais de um ângulo tenha o mesmo lado do terminal. Veja a Figura\(\PageIndex{17}\). O ângulo de 140° é um ângulo positivo, medido no sentido anti-horário. O ângulo de —220° é um ângulo negativo, medido no sentido horário. Mas os dois ângulos têm o mesmo lado terminal. Se dois ângulos na posição padrão tiverem o mesmo lado terminal, eles são ângulos coterminais. Todo ângulo maior que 360° ou menor que 0° é coterminal com um ângulo entre 0° e 360°, e geralmente é mais conveniente encontrar o ângulo coterminal dentro da faixa de 0° a 360° do que trabalhar com um ângulo que esteja fora dessa faixa.
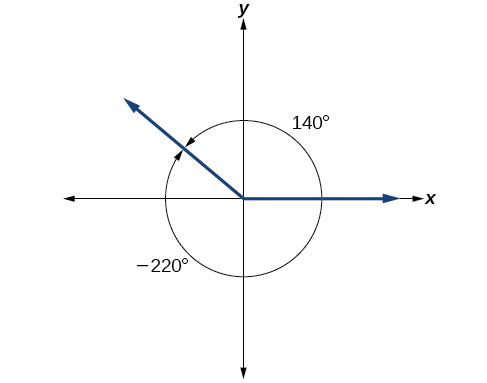
Qualquer ângulo tem infinitos ângulos coterminais porque cada vez que adicionamos 360° a esse ângulo — ou subtraímos 360° dele — o valor resultante tem um lado terminal no mesmo local. Por exemplo, 100° e 460° são coterminais por esse motivo, assim como −260°. Reconhecer que qualquer ângulo tem infinitos ângulos coterminais explica a forma repetitiva nos gráficos das funções trigonométricas.
O ângulo de referência de um ângulo é a medida do menor ângulo agudo positivo\(t\) formado pelo lado terminal do ângulo\(t\) e pelo eixo horizontal. Assim, os ângulos de referência positivos têm lados terminais que estão no primeiro quadrante e podem ser usados como modelos para ângulos em outros quadrantes. Veja a Figura\(\PageIndex{18}\) para exemplos de ângulos de referência para ângulos em diferentes quadrantes.
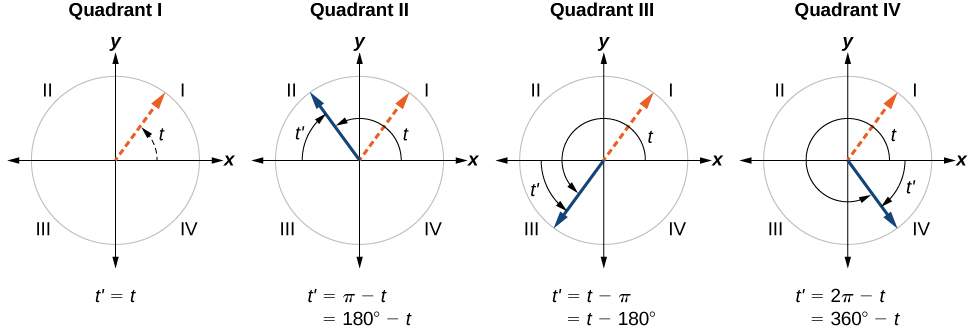
ÂNGULOS COTERMINAIS E DE REFERÊNCIA
- Os ângulos coterminais são dois ângulos na posição padrão que têm o mesmo lado terminal.
- O ângulo de referência de um ângulo é o tamanho do menor ângulo agudo\(t′\), formado pelo lado terminal do ângulo\(t\) e pelo eixo horizontal.
Dado um ângulo maior que 360°, encontre um ângulo coterminal entre 0° e 360°
- Subtraia 360° do ângulo fornecido.
- Se o resultado ainda for maior que 360°, subtraia 360° novamente até que o resultado fique entre 0° e 360°.
- O ângulo resultante é coterminal com o ângulo original.
Exemplo\(\PageIndex{5}\): Finding an Angle Coterminal with an Angle of Measure Greater Than 360°
Encontre o ângulo menos positivo θ que é coterminal com um ângulo medindo 800°, onde\(0°≤θ<360°\).
Solução
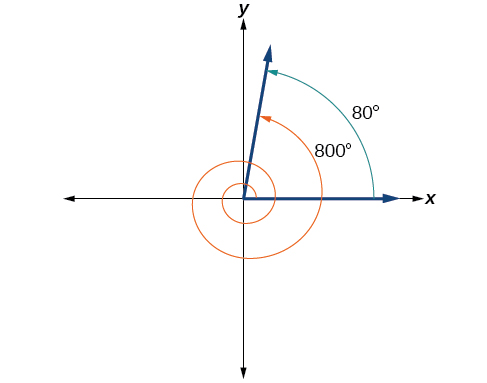
Um ângulo com medida de 800° é coterminal com um ângulo com medida 800 − 360 = 440°, mas 440° ainda é maior que 360°, então subtraímos 360° novamente para encontrar outro ângulo coterminal: 440 − 360 = 80°.
O ângulo\(θ=80°\) é coterminal com 800°. Em outras palavras, 800° é igual a 80° mais duas rotações completas, conforme mostrado na Figura\(\PageIndex{19}\).
\(\PageIndex{5}\)
Encontre um ângulo\(α\) que seja coterminal com um ângulo medindo 870°, onde\(0°≤α<360°\).
Solução
\(α=150°\)
Dado um ângulo com medida menor que 0°, encontre um ângulo coterminal com uma medida entre 0° e 360°.
- Adicione 360° ao ângulo fornecido.
- Se o resultado ainda for menor que 0°, adicione 360° novamente até que o resultado esteja entre 0° e 360°.
- O ângulo resultante é coterminal com o ângulo original.
Exemplo\(\PageIndex{6}\): Finding an Angle Coterminal with an Angle Measuring Less Than 0°
Mostre o ângulo com a medida −45° em um círculo e encontre um ângulo coterminal positivo α tal que 0° ≤ α < 360°.
Solução
Como 45° é metade de 90°, podemos começar no eixo horizontal positivo e medir a metade de um ângulo de 90° no sentido horário.
Como podemos encontrar ângulos coterminais adicionando ou subtraindo uma rotação completa de 360°, podemos encontrar um ângulo coterminal positivo aqui adicionando 360°:
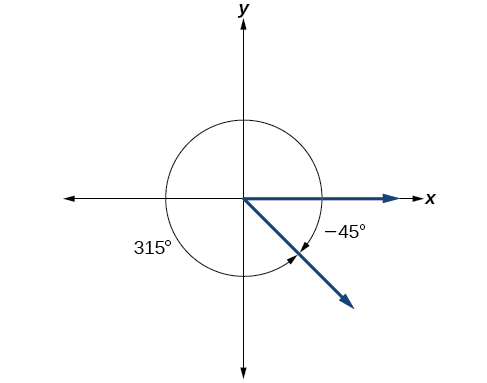
\[−45°+360°=315°\]
Podemos então mostrar o ângulo em um círculo, como na Figura\(\PageIndex{20}\).
\(\PageIndex{6}\)
Encontre um ângulo β que seja coterminal com um ângulo medindo −300° tal que\(0°≤β<360°\).
Solução
\(β=60°\)
Encontrando ângulos coterminais medidos em radianos
Podemos encontrar ângulos coterminais medidos em radianos da mesma forma que os encontramos usando graus. Em ambos os casos, encontramos ângulos coterminais adicionando ou subtraindo uma ou mais rotações completas.
Dado um ângulo maior que\(2\pi\), find a coterminal angle between 0 and \(2\pi\).
- Subtraia\(2π\) do ângulo dado.
- Se o resultado ainda for maior que\(2π\), subtraia\(2π\) novamente até que o resultado esteja entre\(0\)\(2π\) e.
- O ângulo resultante é coterminal com o ângulo original.
Exemplo\(\PageIndex{7}\): Finding Coterminal Angles Using Radians
Encontre um ângulo\(β\) que seja coterminal com\(\frac{19π}{4}\), onde\(0≤β<2π.\)
Solução
Ao trabalhar em graus, encontramos ângulos coterminais adicionando ou subtraindo 360 graus, uma rotação completa. Da mesma forma, em radianos, podemos encontrar ângulos coterminais adicionando ou subtraindo rotações completas de\(2π\) radianos:
\[\begin{align} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{4} \end{align}\]
O ângulo\(\frac{11π}{4}\) é coterminal, mas não menor que\(2π\), então subtraímos outra rotação:
\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \end{align}\]
O ângulo\(\frac{3π}{4}\) é coterminal com\(\frac{19π}{4}\), conforme mostrado na Figura\(\PageIndex{21}\).
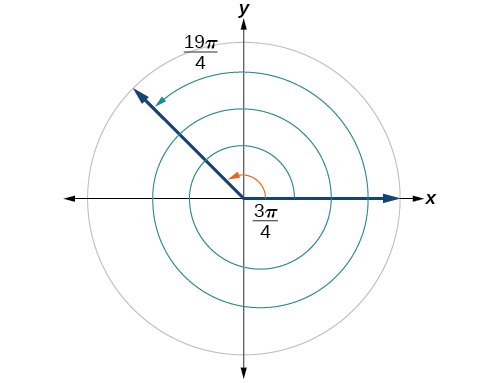
\(\PageIndex{7}\)
Encontre um ângulo de medida\(θ\) que seja coterminal com um ângulo de medida\(−\frac{17π}{6}\) onde\(0≤θ<2π.\)
Solução
\(\frac{7π}{6}\)
Determinando o comprimento de um arco
Lembre-se de que a medida radiana\(θ\) de um ângulo foi definida como a razão entre o comprimento\(s\) do arco de um arco circular e o raio\(r\) do círculo,\(θ=\frac{s}{r}\). A partir dessa relação, podemos encontrar o comprimento do arco ao longo de um círculo, dado um ângulo.
COMPRIMENTO DO ARCO EM UM CÍRCULO
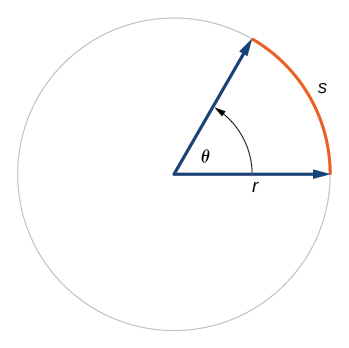
Em um círculo de raio r, o comprimento de um arco\(s\) subtendido por um ângulo com medida\(θ\) em radianos, mostrado na Figura\(\PageIndex{22}\), é
\[s=rθ\]
Dado um círculo de raio\(r,\) calculate the length \(s\) of the arc subtended by a given angle of measure \(θ\).
- Se necessário, converta\(θ\) em radianos.
- Multiplique o raio\(r\) pela medida radiana de\(θ:s=rθ\).
Exemplo\(\PageIndex{8}\): Finding the Length of an Arc
Suponha que a órbita de Mercúrio ao redor do sol seja um círculo perfeito. Mercúrio está a aproximadamente 36 milhões de milhas do sol.
- Em um dia terrestre, Mercúrio completa 0,0114 de sua revolução total. Quantas milhas ele viaja em um dia?
- Use sua resposta da parte (a) para determinar a medida radiana do movimento de Mercúrio em um dia terrestre.
Solução
- Vamos começar encontrando a circunferência da órbita de Mercúrio.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]
Como Mercúrio completa 0,0114 de sua revolução total em um dia terrestre, agora podemos encontrar a distância percorrida:
\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
- Agora, convertemos em radianos:
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]
\(\PageIndex{8}\)
Encontre o comprimento do arco ao longo de um círculo de raio de 10 unidades subtendido por um ângulo de 215°.
Solução
\[\dfrac{215π}{18}=37.525 \text{ units} \]
Encontrando a área de um setor de um círculo
Além do comprimento do arco, também podemos usar ângulos para encontrar a área de um setor de um círculo. Um setor é uma região de um círculo delimitada por dois raios e o arco interceptado, como uma fatia de pizza ou torta. Lembre-se de que a área de um círculo com raio\(r\) pode ser encontrada usando a fórmula\(A=πr^2\). Se os dois raios formarem um ângulo de\(θ\), medido em radianos, então\(\frac{θ}{2π}\) é a razão entre o ângulo medido e a medida de uma rotação completa e, portanto, também é a razão entre a área do setor e a área do círculo. Assim, a área de um setor é a fração\(\frac{θ}{2π}\) multiplicada pela área inteira. (Lembre-se sempre de que essa fórmula só se aplica se\(θ\) estiver em radianos.)
\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]
ÁREA DE UM SETOR
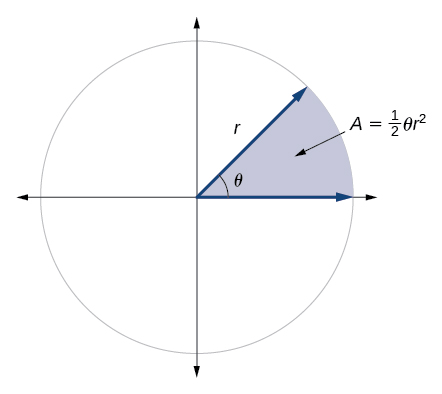
A área de um setor de um círculo com raio\(r\) subtendido por um ângulo\(θ\), medido em radianos, é
\[A=\dfrac{1}{2}θr^2\]
Veja a Figura\(\PageIndex{23}\).
Dado um círculo de raio\(r,\) find the area of a sector defined by a given angle \(θ.\)
- Se necessário, converta\(θ\) em radianos.
- Multiplique metade da medida radiana de\(θ\) pelo quadrado do raio\(r: A=\frac{1}{2}θr^2.\)
Exemplo\(\PageIndex{9}\): Finding the Area of a Sector
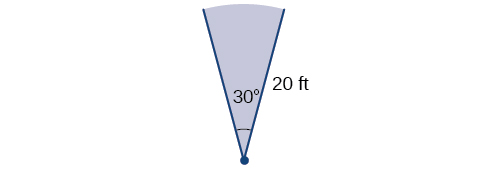
Um aspersor de gramado automático pulveriza uma distância de 20 pés enquanto gira 30 graus, conforme mostrado na Figura\(\PageIndex{24}\). Qual é a área do setor de gramíneas das águas do aspersor?
Solução
Primeiro, precisamos converter a medida do ângulo em radianos. Como 30 graus é um dos nossos ângulos especiais, já conhecemos a medida equivalente em radianos, mas também podemos converter:
\[\begin{align} \text{30 degrees} &=30⋅\frac{π}{180} \\ &=\frac{π}{6} \text{ radians} \end{align}\]
A área do setor é então
\[\begin{align} \text{Area} &= \dfrac{1}{2}(\dfrac{π}{6})(20)^2 \\ & ≈104.72 \end{align}\]
Então, a área é de cerca de\(\mathrm{104.72 \; ft^2}\).
\(\PageIndex{9}\)
Na irrigação por pivô central, um grande tubo de irrigação sobre rodas gira em torno de um ponto central. Um agricultor tem um sistema de pivô central com um raio de 400 metros. Se as restrições de água permitirem que ela regue apenas 150 mil metros quadrados por dia, qual ângulo ela deveria configurar o sistema para cobrir? Escreva a resposta em radianos com duas casas decimais.
Solução
1,88
Use a velocidade linear e angular para descrever o movimento em um caminho circular
Além de encontrar a área de um setor, podemos usar ângulos para descrever a velocidade de um objeto em movimento. Um objeto viajando em um caminho circular tem dois tipos de velocidade. A velocidade linear é a velocidade ao longo de um caminho reto e pode ser determinada pela distância que ela se move (seu deslocamento) em um determinado intervalo de tempo. Por exemplo, se uma roda com raio de 5 polegadas gira uma vez por segundo, um ponto na borda da roda se move a uma distância igual à circunferência, ou 10π polegadas, a cada segundo. Portanto, a velocidade linear do ponto está\(10π\) em. /s. A equação da velocidade linear é a seguinte, onde\(v\) é velocidade linear,\(s\) é deslocamento e\(t\) é tempo.
\[v=\dfrac{s}{t}\]
A velocidade angular resulta do movimento circular e pode ser determinada pelo ângulo pelo qual um ponto gira em um determinado intervalo de tempo. Em outras palavras, a velocidade angular é a rotação angular por unidade de tempo. Então, por exemplo, se uma engrenagem fizer uma rotação completa a cada 4 segundos, podemos calcular sua velocidade angular em\(\frac{360 \text{ degrees}}{4 \text{ seconds}}= \) 90 graus por segundo. A velocidade angular pode ser dada em radianos por segundo, rotações por minuto ou graus por hora, por exemplo. A equação da velocidade angular é a seguinte, onde\(ω\) (lida como ômega) é a velocidade angular,\(θ\) é o ângulo percorrido e\(t\) é o tempo.
\[ω=\dfrac{θ}{t}\]
Combinando a definição de velocidade angular com a equação do comprimento do arco\(s=rθ\), podemos encontrar uma relação entre velocidades angulares e lineares. A equação da velocidade angular pode ser resolvida\(θ\), dando\(θ=ωt.\) Substituindo isso na equação do comprimento do arco, obtém-se:
\[\begin{align}s &=rθ \\ &=rωt \end{align}\]
Substituindo isso na equação de velocidade linear, obtém-se:
\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]
VELOCIDADE ANGULAR E LINEAR
Conforme um ponto se move ao longo de um círculo de raio,\(r,\) sua velocidade angular\(ω\),, é a rotação angular\(θ\) por unidade de tempo,\(t\).
\[ω=\dfrac{θ}{t}\]
A velocidade linear. \(v\), do ponto pode ser encontrado como a distância percorrida, comprimento do arco\(s\), por unidade de tempo,\(t.\)
\[v=\frac{s}{t}\]
Quando a velocidade angular é medida em radianos por unidade de tempo, a velocidade linear e a velocidade angular são relacionadas pela equação
\[v=rω\]
Essa equação afirma que a velocidade angular em radianos\(ω\), representando a quantidade de rotação que ocorre em uma unidade de tempo, pode ser multiplicada pelo raio\(r\) para calcular o comprimento total do arco percorrido em uma unidade de tempo, que é a definição de velocidade linear.
Dada a quantidade de rotação angular e o tempo decorrido, calcule a velocidade angular
- Se necessário, converta a medida do ângulo em radianos.
- Divida o ângulo em radianos pelo número de unidades de tempo decorridas:\(ω=\frac{θ}{t}.\)
- A velocidade resultante será em radianos por unidade de tempo.
Exemplo\(\PageIndex{10}\): Finding Angular Speed
Uma roda d'água, mostrada na Figura\(\PageIndex{25}\), completa 1 rotação a cada 5 segundos. Determine a velocidade angular em radianos por segundo.
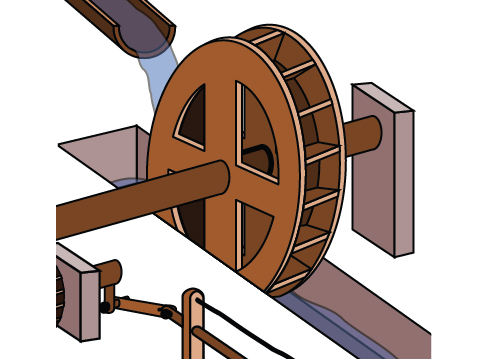
Solução
A roda completa 1 rotação ou passa por um ângulo de\(2π\) radianos em 5 segundos, então a velocidade angular seria\(ω=\frac{2π}{5}≈1.257\) radianos por segundo.
\(\PageIndex{10}\)
Um disco de vinil antigo é tocado em uma mesa giratória girando no sentido horário a uma taxa de 45 rotações por minuto. Determine a velocidade angular em radianos por segundo.
Solução
\(−\frac{3π}{2}\)rad/s
Dado o raio de um círculo, um ângulo de rotação e uma duração do tempo decorrido, determine a velocidade linear
- Converta a rotação total em radianos, se necessário.
- Divida a rotação total em radianos pelo tempo decorrido para encontrar a velocidade angular: aplique\(ω=\frac{θ}{t}\).
- Multiplique a velocidade angular pelo comprimento do raio para encontrar a velocidade linear, expressa em termos da unidade de comprimento usada para o raio e da unidade de tempo usada para o tempo decorrido: aplique\(v=rω\).
Exemplo\(\PageIndex{11}\): Finding a Linear Speed
Uma bicicleta tem rodas de 28 polegadas de diâmetro. Um tacômetro determina que as rodas estão girando a 180 RPM (rotações por minuto). Descubra a velocidade em que a bicicleta está percorrendo a estrada.
Solução
Aqui, temos uma velocidade angular e precisamos encontrar a velocidade linear correspondente, já que a velocidade linear da parte externa dos pneus é a velocidade com que a bicicleta percorre a estrada.
Começamos convertendo de rotações por minuto em radianos por minuto. Pode ser útil utilizar as unidades para fazer essa conversão:
\[\mathrm{180 \dfrac{\cancel{rotations}}{minute}⋅\dfrac{2π \; radians}{\cancel{rotation}}=360π\dfrac{radians}{minute}}\]
Usando a fórmula acima junto com o raio das rodas, podemos encontrar a velocidade linear:
\[\begin{align} v & =(14 \text{ inches})(360π \dfrac{\text{radians}}{\text{minute}}) \\ &=5040π \dfrac{\text{inches}}{\text{minute}} \end{align}\]
Lembre-se de que os radianos são uma medida sem unidades, portanto, não é necessário incluí-los. Medida sem unidade, portanto, não é necessário incluí-los.
Finalmente, podemos querer converter essa velocidade linear em uma medida mais familiar, como milhas por hora.
\[\mathrm{5040π\dfrac{\cancel{inches}}{\cancel{minute}}⋅\dfrac{1 \; \cancel{ feet}}{12 \; \cancel{ inches}}⋅\dfrac{1 \; \cancel{ mile}}{5280 \cancel{ feet}}⋅\dfrac{60 \cancel{ minutes}}{1 \; hour}≈14.99 \; miles \; per \; hour \; (mph)}\]
![]() \(\PageIndex{11}\)
\(\PageIndex{11}\)
Um satélite está girando ao redor da Terra a 0,25 radianos por hora a uma altitude de 242 km acima da Terra. Se o raio da Terra for de 6378 quilômetros, encontre a velocidade linear do satélite em quilômetros por hora.
Solução
1655 quilômetros por hora
Mídia
Acesse esses recursos on-line para obter instruções e práticas adicionais com ângulos, comprimento do arco e áreas de setores.
Equações-chave
| comprimento do arco | \(s=rθ\) |
| area of a sector | \(A=\frac{1}{2}θr^2\) |
| angular speed | \(ω=\frac{θ}{t}\) |
| linear speed | \(v=\frac{s}{t}\) |
| linear speed related to angular speed | \(v=rω\) |
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
- To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents. See Example.
- In addition to degrees, the measure of an angle can be described in radians. See Example.
- To convert between degrees and radians, use the proportion \(\frac{θ}{180}=\frac{θ^R}{π}\). See Example and Example.
- Two angles that have the same terminal side are called coterminal angles.
- We can find coterminal angles by adding or subtracting 360° or \(2π\). See Example and Example.
- Coterminal angles can be found using radians just as they are for degrees. See Example.
- The length of a circular arc is a fraction of the circumference of the entire circle. See Example.
- The area of sector is a fraction of the area of the entire circle. See Example.
- An object moving in a circular path has both linear and angular speed.
- The angular speed of an object traveling in a circular path is the measure of the angle through which it turns in a unit of time. See Example.
- The linear speed of an object traveling along a circular path is the distance it travels in a unit of time. See Example.
Glossary
- angle
- the union of two rays having a common endpoint
- angular speed
- the angle through which a rotating object travels in a unit of time
- arc length
- the length of the curve formed by an arc
- area of a sector
- area of a portion of a circle bordered by two radii and the intercepted arc; the fraction \(\frac{θ}{2π}\) multiplied by the area of the entire circle
- coterminal angles
- description of positive and negative angles in standard position sharing the same terminal side
- degree
- a unit of measure describing the size of an angle as one-360th of a full revolution of a circle
- initial side
- the side of an angle from which rotation begins
- linear speed
- the distance along a straight path a rotating object travels in a unit of time; determined by the arc length
- measure of an angle
- the amount of rotation from the initial side to the terminal side
- negative angle
- description of an angle measured clockwise from the positive x-axis
- positive angle
- description of an angle measured counterclockwise from the positive x-axis
- quadrantal angle
- an angle whose terminal side lies on an axis
- radian measure
- the ratio of the arc length formed by an angle divided by the radius of the circle
- radian
- the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle
- ray
- one point on a line and all points extending in one direction from that point; one side of an angle
- reference angle
- the measure of the acute angle formed by the terminal side of the angle and the horizontal axis
- standard position
- the position of an angle having the vertex at the origin and the initial side along the positive x-axis
- terminal side
- the side of an angle at which rotation ends
- vertex
- the common endpoint of two rays that form an angle


