Home
Idioma Portugues
Pré-cálculo (OpenStax)
12: Introdução ao cálculo
12.2: Encontrando limites - Propriedades dos limites

12.2: Encontrando limites - Propriedades dos limites

Last updated
Save as PDF

Page ID: 189247

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considere a função racional

\[f(x)=\dfrac{x^2−6x−7}{x−7} \nonumber \]

A função pode ser fatorada da seguinte forma:

\[f(x)=\dfrac{\cancel{(x−7)}(x+1)}{\cancel{x−7}} \nonumber \]

o que nos dá

\[f(x)=x+1,x≠7. \nonumber \]

Isso significa que a função$f(x)$ é a mesma que a função?$g(x)=x+1?$

A resposta é não. $f(x)$A função não tem$x=7$ em seu domínio, mas$g(x)$ sim. Graficamente, observamos que há um furo no gráfico de$f(x)$ at$x=7$, conforme mostrado na Figura, e nenhum buraco no gráfico de$g(x)$, conforme mostrado na Figura.

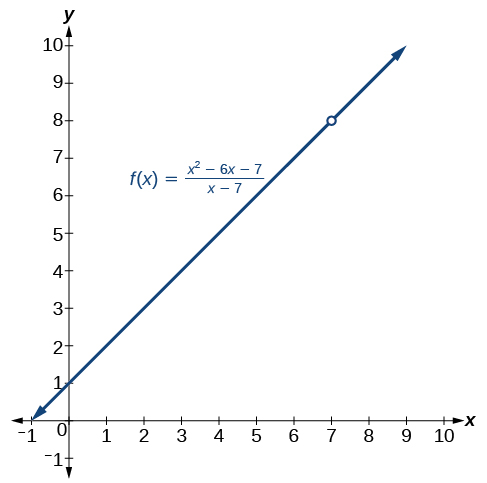
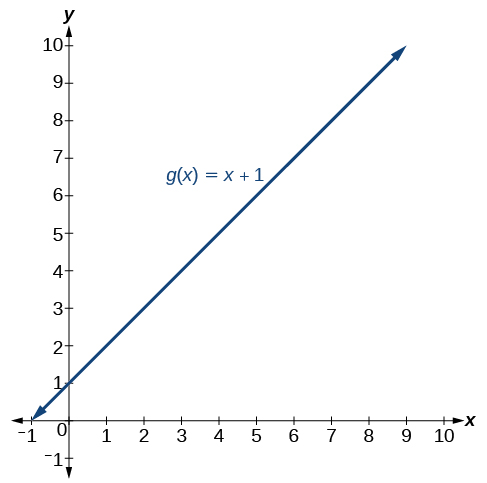
$CNX_Precalc_Figure_12_02_001.jpg$ $CNX_Precalc_Figure_12_02_002.jpg$

(esquerda) O gráfico da função$f$ contém uma quebra em$x=7$ e, portanto, não é contínuo em$x=7$. (Direita) O gráfico da função$g$ é contínuo.

Então, essas duas funções diferentes também têm limites diferentes quando$x$ se aproxima de 7? Não necessariamente. Lembre-se de que, ao determinar o limite de uma função à medida que se$x$ aproxima$a$, o que importa é se a saída se aproxima de um número real à medida que nos aproximamos$x=a$. A existência de um limite não depende do que acontece quando$x$ é igual$a$.

Veja novamente a Figura e a Figura. Observe que em ambos os gráficos, quando$x$ se aproxima de 7, os valores de saída se aproximam de 8. Isso significa

\[ \lim \limits_{x \to 7} f(x)= \lim \limits_{x \to 7} g(x). \nonumber \]

Lembre-se de que, ao determinar um limite, a preocupação é o que ocorre próximo$x=a$, não em$x=a$. Nesta seção, usaremos uma variedade de métodos, como reescrever funções por fatoração, para avaliar o limite. Esses métodos nos darão uma verificação formal do que anteriormente realizávamos por intuição.

Encontrando o limite de uma soma, uma diferença e um produto

Representar graficamente uma função ou explorar uma tabela de valores para determinar um limite pode ser complicado e demorado. Quando possível, é mais eficiente usar as propriedades dos limites, que é uma coleção de teoremas para encontrar limites.

Conhecer as propriedades dos limites nos permite calcular os limites diretamente. Podemos somar, subtrair, multiplicar e dividir os limites das funções como se estivéssemos realizando as operações nas próprias funções para encontrar o limite do resultado. Da mesma forma, podemos determinar o limite de uma função elevada a uma potência aumentando o limite para essa potência. Também podemos encontrar o limite da raiz de uma função tomando a raiz do limite. Usando essas operações em limites, podemos encontrar os limites de funções mais complexas encontrando os limites de suas funções de componentes mais simples.

propriedades dos limites

Seja$a, k, A,$ e$B$ represente números reais, e$f$ e$g$ seja funções, de tal forma que$\lim \limits_{x \to a} f(x)=A$ e$ \lim \limits_{x \to a}g(x)=B.$ Para limites que existem e são finitos, as propriedades dos limites estão resumidas na Tabela

Constante, k	$\lim \limits_{x \to a} k=k $
Vezes constantes de uma função	$\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA$
Soma das funções	$\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B$
Diferença de funções	$\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B$
Produto de funções	$ \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B$
Quociente de funções	$\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0$
Função elevada a um expoente	$\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n$, onde$n$ é um número inteiro positivo
n na raiz de uma função, onde n é um número inteiro positivo	$\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}$
Função polinomial	$ \lim \limits _{x \to a} p(x)=p(a)$

Exemplo$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Avalie\[\lim \limits _{x \to 3}(2x+5). \nonumber \]

Solução

\[\begin{align} \lim \limits _{x \to 3}(2x+5) &= \lim \limits _{x \to 3} (2x)+\lim \limits _{x \to 3}(5) && \text{Sum of functions property} \\ &=2 \lim \limits_{ x \to 3}(x)+\lim \limits _{x \to 3}(5) && \text{Constant times a function property} \\ &=2(3)+5 && \text{Evaluate} \\ &=11 \end{align} \nonumber \]

Exercício$\PageIndex{1}$:

Avalie o seguinte limite:\[\lim \limits_{x \to −12}(−2x+2). \nonumber \]

Solução

Encontrando o limite de um polinômio

Nem todas as funções ou seus limites envolvem simples adição, subtração ou multiplicação. Alguns podem incluir polinômios. Lembre-se de que um polinômio é uma expressão que consiste na soma de dois ou mais termos, cada um dos quais consiste em uma constante e uma variável elevada a uma potência integral não negativa. Para encontrar o limite de uma função polinomial, podemos encontrar os limites dos termos individuais da função e, em seguida, somá-los. Além disso, o limite de uma função polinomial como$x$ abordagens$a$ é equivalente a simplesmente avaliar a função para$a$.

como: Dada uma função contendo um polinômio, encontre seu limite

Use as propriedades dos limites para dividir o polinômio em termos individuais.
Encontre os limites dos termos individuais.
Adicione os limites.
Como alternativa, avalie a função para$a$.

Exemplo$\PageIndex{1}$: Evaluating the Limit of a Function Algebraically

Avalie\[ \lim \limits_{x \to 3}(5x ^2). \nonumber \]

Solução

\[\begin{align} \lim \limits_{x \to 3}(5x^2) &= 5 \lim \limits_{x \to 3}(x^2) && \text{Constant times a function property} \\ &=5(3^2) && \text{Function raised to an exponent property} \\&=45 \end{align} \nonumber \]

Exercício$\PageIndex{1}$:

Avalie\[ \lim \limits_{x \to 4} (x^3−5). \nonumber \]

Solução

Exemplo$\PageIndex{2}$: Evaluating the Limit of a Polynomial Algebraically

Avalie\[ \lim \limits_{x \to 5} (2x^3−3x+1). \nonumber \]

Solução

\[\begin{align} \lim \limits_{x \to 5}(2x^3−3x+1) &= \lim \limits_{x \to 5}(2x3)−\lim \limits_{x \to 5}(3x)+\lim \limits_{x \to 5} (1) && \text{Sum of functions}\\ &= 2 \lim \limits_{x \to 5}(x^3)−3 \lim \limits_{x \to 5}(x)+\lim \limits_{x \to 5}(1) && \text{Constant times a function} \\ &=2(5^3)−3(5)+1 && \text{Function raised to an exponent} \\ &=236 &&\text{Evaluate} \end{align} \nonumber \]

Exercício$\PageIndex{2}$:

Avalie o seguinte limite:\[\lim \limits_{x \to −1}(x^4−4x^3+5). \nonumber \]

Solução

Encontrando o limite de um poder ou de uma raiz

Quando um limite inclui uma potência ou uma raiz, precisamos de outra propriedade para nos ajudar a avaliá-la. O quadrado do limite de uma função é igual ao limite do quadrado da função; o mesmo vale para potências mais altas. Da mesma forma, a raiz quadrada do limite de uma função é igual ao limite da raiz quadrada da função; o mesmo vale para raízes mais altas.

Exemplo$\PageIndex{3}$: Evaluating a Limit of a Power

Avalie\[ \lim \limits_{x \to 2}(3x+1)^5. \nonumber \]

Solução

Tomaremos o limite da função quando$x$ se aproximar de 2 e elevaremos o resultado para a ^5ª potência.

\[\begin{align} \lim \limits_{x \to 2} (3x+1)^5 &= (\lim \limits_{x \to 2}(3x+1))^5 \\ &=(3(2)+1)^5 \\ &=7^5 \\ &=16,807 \end{align} \nonumber \]

Exercício$\PageIndex{3}$:

Avalie o seguinte limite:$ \lim \limits_{x \to −4}(10x+36)^3.$

Solução

−64

Perguntas e respostas: Se não pudermos aplicar diretamente as propriedades de um limite, por exemplo, em$\lim \limits_{x \to 2}(\frac{x^2+6x+8}{x−2})$, can we still determine the limit of the function as $x$ approaches $a$?

Sim. Algumas funções podem ser reorganizadas algebricamente para que se possa avaliar o limite de uma forma equivalente simplificada da função.

Encontrando o limite de um quociente

Encontrar o limite de uma função expresso como um quociente pode ser mais complicado. Muitas vezes precisamos reescrever a função algebricamente antes de aplicar as propriedades de um limite. Se o denominador for avaliado como 0 quando aplicamos as propriedades de um limite diretamente, devemos reescrever o quociente em uma forma diferente. Uma abordagem é escrever o quociente na forma fatorada e simplificar.

Exemplo$\PageIndex{4}$: Evaluating the Limit of a Quotient by Factoring

Avalie\[\lim \limits_{x \to 2} (\frac{x^2−6x+8}{x−2}). \nonumber \]

Solução

Considere sempre que possível e simplifique.

\[\begin{align} \lim \limits_{x \to 2} (\dfrac{x^2−6x+8}{x−2}) &= \lim \limits_{x \to 2}(\dfrac{(x−2)(x−4)}{x−2}) && \text{Factor the numerator.} \\ & = \lim \limits_{x \to 2}(\dfrac{\cancel{(x−2)}(x−4)}{\cancel{x−2}}) && \text{Cancel the common factors.} \\ &= \lim \limits_{x \to 2}(x−4) && \text{Evaluate.} \\ & =2−4=−2 \end{align} \nonumber \]

Análise

Quando o limite de uma função racional não pode ser avaliado diretamente, as formas fatoradas do numerador e do denominador podem ser simplificadas para um resultado que pode ser avaliado.

Observe, a função

\[f(x)=\dfrac{x^2−6x+8}{x−2} \nonumber \]

é equivalente à função

\[f(x)=x−4,x≠2. \nonumber \]

Observe que o limite existe mesmo que a função não esteja definida em$x = 2$.

Exercício$\PageIndex{4}$

Avalie o seguinte limite:\[\lim \limits_{x \to 7} \left( \dfrac{x^2−11x+28}{7−x} \right) . \nonumber \]

Solução

$−3$

Exemplo$\PageIndex{5}$: Evaluating the Limit of a Quotient by Finding the LCD

Avalie\[\lim \limits_{x \to 5} \left( \dfrac{\frac{1}{x}−\frac{1}{5}}{x−5} \right) . \nonumber \]

Solução

Encontre o LCD para os denominadores dos dois termos no numerador e converta as duas frações para ter o LCD como denominador.

Análise

Ao determinar o limite de uma função racional que tem termos adicionados ou subtraídos no numerador ou no denominador, o primeiro passo é encontrar o denominador comum dos termos somados ou subtraídos; em seguida, converta os dois termos para ter esse denominador ou simplificar a função racional multiplicando numerador e denominador pelo denominador menos comum. Em seguida, verifique se o numerador e o denominador resultantes têm algum fator comum.

Exercício$\PageIndex{5}$:

Avalie\[\lim \limits_{x \to −5} \left( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right). \nonumber \]

Solução

$−\frac{1}{50}$

como: Dado o limite de uma função contendo uma raiz, use um conjugado para avaliar

Se o quociente fornecido não estiver na$(\frac{0}{0})$ forma indeterminada, avalie diretamente.
Caso contrário, reescreva a soma (ou diferença) de dois quocientes como um único quociente, usando o menor denominador comum (LCD).
Se o numerador incluir uma raiz, racionalize o numerador; multiplique o numerador e o denominador pelo conjugado do numerador. Lembre-se de que$a±\sqrt{b}$ são conjugados.
Simplifique.
Avalie o limite resultante.

Exemplo$\PageIndex{6}$: Evaluating a Limit Containing a Root Using a Conjugate

Avalie\[ \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x} −5}{x} \right) . \nonumber \]

Solução

\[\begin{align} \lim \limits_{x \to 0} \left( \dfrac{\sqrt{25−x}−5}{x} \right) &= \lim \limits_{x \to 0} \left( \dfrac{(\sqrt{25−x}−5)}{x}⋅\frac{(\sqrt{25−x}+5)}{(\sqrt{25−x}+5)} \right) && \text{Multiply numerator and denominator by the conjugate.} \\ &= \lim \limits_{x \to 0} \left( \dfrac{(25−x)−25}{x(\sqrt{25−x}+5)} \right) && \text{Multiply: } (\sqrt{25−x} −5)⋅(\sqrt{25−x}+5)=(25−x)−25. \\ & = \lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(25−x+5)} \right) && \text{Combine like terms.} \\ & =\lim \limits_{x \to 0} \left( \dfrac{−\cancel{x}}{\cancel{x}(\sqrt{25−x}+5)} \right) && \text{Simplify }\dfrac{−x}{x}=−1. \\ & =\dfrac{−1}{\sqrt{25−0}+5} && \text{Evaluate.} \\ & =\dfrac{−1}{5+5}=−\dfrac{1}{10} \end{align} \nonumber \]

Análise

Ao determinar um limite de uma função com uma raiz como um dos dois termos em que não podemos calcular diretamente, pense em multiplicar o numerador e o denominador pelo conjugado dos termos.

Exercício$\PageIndex{6}$

Avalie o seguinte limite:$\lim \limits_{h \to 0} \left( \dfrac{\sqrt{16−h}−4}{h} \right) $.

Solução

$−\frac{1}{8}$

Exemplo$\PageIndex{7}$: Evaluating the Limit of a Quotient of a Function by Factoring

Avalie\[\lim \limits_{x \to 4} \left( \frac{4−x}{\sqrt{x−2}} \right). \nonumber \]

Solução

\[\begin{align} \lim \limits_{x \to 4} (\dfrac{4−x}{\sqrt{x}−2}) & = \lim \limits_{x \to 4} (\dfrac{(2+\sqrt{x})(2−x)}{\sqrt{x}−2}) && \text{Factor.} \\ &= \lim \limits_{x \to 4} ( \dfrac{(2+\sqrt{x})(\cancel{2−\sqrt{x}})}{−\cancel{(2−\sqrt{x})}}) && \text{Factor −1 out of the denominator. Simplify.} \\ & = \lim \limits_{x \to 4}−(2+x) && \text{Evaluate.} \\ &=−(2+ \sqrt{4}) \\ &=−4 \end{align} \nonumber \]

Análise

Multiplicar por um conjugado expandiria o numerador; em vez disso, procure fatores no numerador. Quatro é um quadrado perfeito para que o numerador esteja na forma

\[a^2−b^2 \nonumber \]

e pode ser considerado como

\[(a+b)(a−b). \nonumber \]

Exercício$\PageIndex{7}$

Avalie o seguinte limite:\[\lim \limits_{x \to 3} \left( \frac{x−3}{\sqrt{x}−\sqrt{3} }\right). \nonumber \]

Solução

$2\sqrt{3}$

como: Dado um quociente com valores absolutos, avalie seu limite

Tente fatorar ou encontrar o LCD.
Se o limite não puder ser encontrado, escolha vários valores próximos e em ambos os lados da entrada em que a função esteja indefinida.
Use a evidência numérica para estimar os limites em ambos os lados.

Exemplo$\PageIndex{8}$: Evaluating the Limit of a Quotient with Absolute Values

Avalie\[\lim \limits_{x \to 7} \frac{|x−7|}{x−7}. \nonumber \]

Solução

A função é indefinida em$x=7$, então vamos tentar valores próximos a 7 da esquerda e da direita.

Limite esquerdo:\[\frac{|6.9−7|}{6.9−7}=\frac{|6.99−7|}{6.99−7}=\frac{|6.999−7|}{6.999−7}=−1 \nonumber \]

Limite à direita:\[\frac{|7.1−7|}{7.1−7}=\frac{|7.01−7|}{7.01−7}=\frac{|7.001−7|}{7.001−7}=1 \nonumber \]

Como os limites esquerdo e direito não são iguais, não há limite.

Exercício$\PageIndex{8}$

Avalie\[ \lim \limits_{x \to 6^+} \frac{6−x}{| x−6 |}. \nonumber \]

Solução

Conceitos-chave

As propriedades dos limites podem ser usadas para realizar operações nos limites das funções, e não nas próprias funções. Veja o exemplo.
O limite de uma função polinomial pode ser encontrado encontrando a soma dos limites dos termos individuais. Veja o exemplo e o exemplo.
O limite de uma função que foi elevado a uma potência é igual à mesma potência do limite da função. Outro método é a substituição direta. Veja o exemplo.
O limite da raiz de uma função é igual à raiz correspondente do limite da função.
Uma forma de encontrar o limite de uma função expressa como um quociente é escrever o quociente na forma fatorada e simplificar. Veja o exemplo.
Outro método para encontrar o limite de uma fração complexa é encontrar o LCD. Veja o exemplo.
Um limite contendo uma função contendo uma raiz pode ser avaliado usando um conjugado. Veja o exemplo.
Os limites de algumas funções expressos como quocientes podem ser encontrados por fatoração. Veja o exemplo.
Uma forma de avaliar o limite de um quociente contendo valores absolutos é usando evidências numéricas. Configurá-lo por partes também pode ser útil. Veja o exemplo.

Glossário

propriedades dos limites: uma coleção de teoremas para encontrar limites de funções executando operações matemáticas nos limites

Constante, k	\(\lim \limits_{x \to a} k=k \)
Vezes constantes de uma função	\(\lim \limits_{x \to a} [k⋅f(x)]=k \lim \limits_{x \to a} f(x)=kA\)
Soma das funções	\(\lim \limits_{x \to a} [f(x)+g(x)]= \lim \limits_{x \to a}f(x)+ \lim \limits_{x to a} g(x)=A+B\)
Diferença de funções	\(\lim \limits_{x \to a} [f(x)−g(x)]= \lim \limits_{x \to a} f(x)− \lim \limits_{x \to a} g(x)=A−B\)
Produto de funções	\( \lim \limits _{x \to a}[f(x)⋅g(x)]= \lim \limits _{x \to a}f(x)⋅ \lim \limits_{x \to a} g(x)=A⋅B\)
Quociente de funções	\(\lim \limits _{x \to a} \frac{f(x)}{g(x)}= \frac{\lim \limits _{x \to a}f(x) }{\lim \limits _{x \to a}g(x)}=\frac{A}{B},B≠0\)
Função elevada a um expoente	\(\lim \limits _{x \to a}[f(x)]^n=[\lim \limits _{x \to ∞}f(x)]^n=A^n\), onde\(n\) é um número inteiro positivo
n na raiz de uma função, onde n é um número inteiro positivo	\(\lim \limits _{x \to a}f(x) \sqrt[n]{f(x)} = \sqrt[n]{ \lim \limits _{x \to a}[ f(x) ]}=\sqrt[n]{A}\)
Função polinomial	\( \lim \limits _{x \to a} p(x)=p(a)\)