12.3: Continuidade

Last updated
Save as PDF

Page ID: 189235

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

O Arizona é conhecido por seu calor seco. Em um determinado dia, a temperatura pode subir$118^∘F$ e cair apenas para um ritmo acelerado. A$95^∘F.$ figura$\PageIndex{1}$ mostra a função$T$, onde a saída de$T(x)$ é a temperatura em graus Fahrenheit e a entrada$x$ é a hora do dia, usando um relógio de 24 horas em um dia de verão específico.

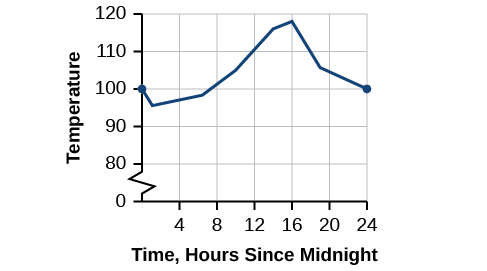
$CNX_Precalc_Figure_12_03_001.jpg$

Figura$\PageIndex{1}$: A temperatura em função do tempo forma uma função contínua.

Quando analisamos esse gráfico, notamos uma característica específica. Não há quebras no gráfico. Poderíamos traçar o gráfico sem pegar nosso lápis. Essa única observação nos diz muito sobre a função. Nesta seção, investigaremos funções com e sem interrupções.

Determinando se uma função é contínua em um número

Vamos considerar um exemplo específico de temperatura em termos de data e localização, como 27 de junho de 2013, em Phoenix, AZ. O gráfico na Figura$\PageIndex{1}$ indica que, às 2 da manhã, a temperatura era$96 ^∘F$. Por volta das 14h, a temperatura subiu para$116^∘F,$ e às 16h já era.$118 ^∘F.$ Em algum momento, entre 2h e 16h, a temperatura externa deve ter sido exatamente$110.5 ^∘ F$. De fato, qualquer temperatura entre$96 ^∘ F$ e$118 ^∘ F$ ocorreu em algum momento daquele dia. Isso significa que todos os números reais na saída entre$96 ^∘ F$ e$118 ^∘ F$ são gerados em algum ponto pela função de acordo com o teorema do valor intermediário,

Veja novamente a Figura$\PageIndex{1}$. Não há quebras no gráfico da função nesse período de 24 horas. Em nenhum momento a temperatura deixou de existir, nem houve um ponto em que a temperatura saltasse instantaneamente em vários graus. Uma função que não tem furos ou quebras em seu gráfico é conhecida como função contínua. A temperatura em função do tempo é um exemplo de função contínua.

Se a temperatura representa uma função contínua, que tipo de função não seria contínua? Considere um exemplo de dólares expressos em função das horas de estacionamento. Vamos criar a função$D$, onde$D(x)$ está a saída representando o custo em dólares para o$x$ número de horas de estacionamento (Figura$\PageIndex{2}$).

Suponha que uma garagem cobra $4,00 por hora ou fração de hora, com uma taxa máxima de $25 por dia. Estacione por duas horas e cinco minutos e a taxa é de $12. Estacione mais uma hora e a taxa é de $16. Nunca poderemos ser cobrados $13, $14 ou $15. Existem números reais entre 12 e 16 que a função nunca gera. Há quebras no gráfico da função para esse período de 24 horas, pontos em que o preço do estacionamento sobe instantaneamente em vários dólares.

Figura$\PageIndex{2}$: As taxas de estacionamento formam uma função descontínua.

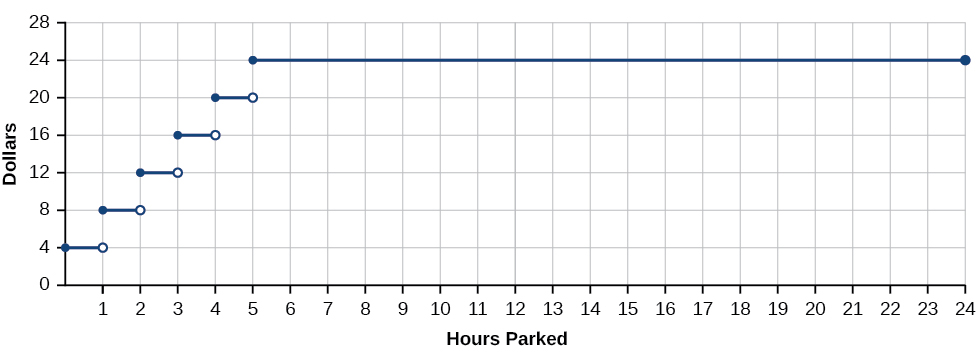
Uma função que permanece nivelada por um intervalo e depois salta instantaneamente para um valor mais alto é chamada de função gradual. Essa função é um exemplo.

Uma função que tem qualquer furo ou quebra em seu gráfico é conhecida como função descontínua. Uma função gradual, como taxas de estacionamento em função das horas estacionadas, é um exemplo de função descontínua.

Então, como podemos decidir se uma função é contínua em um determinado número? Podemos verificar três condições diferentes. Vamos usar a função$y=f(x)$ representada na Figura como exemplo.

Figure_12_03_003">A figura se aproxima$x=a$ da esquerda e da direita, a mesma coordenada y é abordada. Portanto, a Condição 2 está satisfeita. No entanto, ainda pode haver um buraco no gráfico em$x=a$.

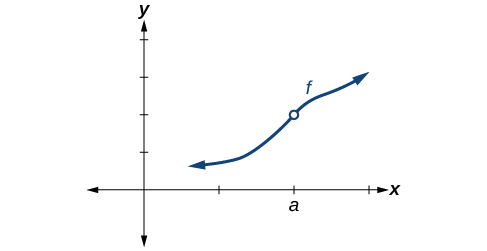
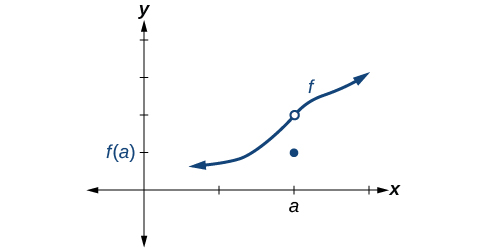
Condição 3 De acordo com a Condição 3, a coordenada y y correspondente em$x=a$ preenche o orifício no gráfico de$f$. Isso está escrito$\lim \limits_{x \to a} f(x)=f(a)$.

Satisfazer todas as três condições significa que a função é contínua. Todas as três condições são satisfeitas para a função representada na Figura, então a função é contínua como$x=a$.

Todas as três condições estão satisfeitas. A função é contínua em$x=a$.

Figura a Figura fornece vários exemplos de gráficos de funções que não são contínuas$x=a$ e a condição ou condições que falham.

A condição 2 está satisfeita. Ambas as condições 1 e 3 falham.

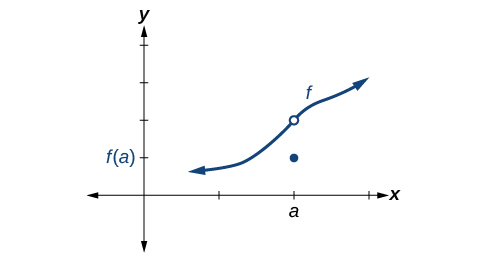
$CNX_Precalc_Figure_12_03_007.jpg$

Ambas as condições 1 e 2 estão satisfeitas. A condição 3 falha.

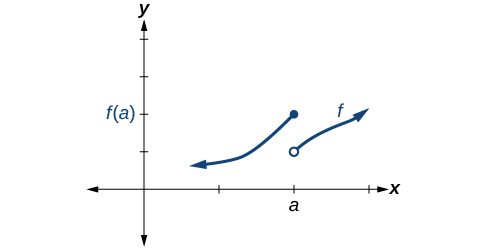
$CNX_Precalc_Figure_12_03_008.jpg$

A condição 1 está satisfeita. As condições 2 e 3 falham.

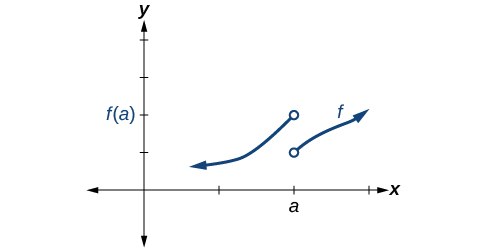
$CNX_Precalc_Figure_12_03_009.jpg$

Todas as condições 1, 2 e 3 falham.

Definição de continuidade

Uma função$f(x)$ é contínua$x=a$ desde que todas as três condições a seguir sejam verdadeiras:

Condição 1:$f(a)$ existe.
Condição 2:$\lim \limits_{x \to a} f(x)$ existe em$x=a$.
Condição 3:$\lim \limits_{x \to a} f(x)=f(a)$

Se uma função não$f(x)$ for contínua em$x=a$, a função será descontínua em$x=a$.

Identificando uma descontinuidade de salto

A descontinuidade pode ocorrer de maneiras diferentes. Vimos na seção anterior que uma função poderia ter um limite à esquerda e um limite à direita, mesmo que não fossem iguais. Se os limites esquerdo e direito existirem, mas forem diferentes, o gráfico “salta” para$x=a$. Diz-se que a função tem uma descontinuidade de salto.

Como exemplo, veja o gráfico da função$y=f(x)$ na Figura. Observe, à medida que$x$ se aproxima,$a$ como a saída se aproxima de valores diferentes da esquerda e da direita.

Gráfico de uma função com uma descontinuidade de salto.

DESCONTINUIDADE DO JUMP

Uma função$f(x)$ tem uma descontinuidade de salto$x=a$ se os limites esquerdo e direito existirem, mas não forem iguais:$ \lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

Identificando a descontinuidade removível

Algumas funções têm uma descontinuidade, mas é possível redefinir a função nesse ponto para torná-la contínua. Diz-se que esse tipo de função tem uma descontinuidade removível. Vamos ver a função$y=f(x)$ representada pelo gráfico na Figura. A função tem um limite. No entanto, há um buraco em$x=a$. O buraco pode ser preenchido estendendo o domínio para incluir a entrada$x=a$ e definindo a saída correspondente da função nesse valor como o limite da função em$x=a$.

Gráfico da função$f$ com uma descontinuidade removível em$x=a$.

descontinuidade removível

Uma função f (x) f (x) tem uma descontinuidade removível em$x=a$ se o limite$\lim \limits_{x \to a} f(x),$ existir, mas

$f(a)$não existe ou
$f(a)$, o valor da função at$x=a$ não é igual ao limite,$f(a)≠ \lim \limits_{x \to a} f(x)$.

Exemplo$\PageIndex{1}$: Identifying Discontinuities

Identifique todas as descontinuidades das seguintes funções como um salto ou uma descontinuidade removível.

$f(x)=\frac{x^2−2x−15}{x−5}$
\[ g(x)= \begin{cases} x+1, & x<2 \\ −x, & x≥2 \end{cases} \]

Observe que a função está definida em todos os lugares, exceto em$x=5$.
Portanto,$f(5)$ não existe, a Condição 2 não está satisfeita. Como a Condição 1 é satisfeita, o limite quando$x$ se aproxima de 5 é 8 e a Condição 2 não é satisfeita. Isso significa que há uma descontinuidade removível em$x=5$.
A condição 2 é satisfeita porque$g(2)=−2.$
Observe que a função é uma função por partes e, para cada peça, a função é definida em todos os lugares em seu domínio. Vamos examinar a Condição 1 determinando os limites esquerdo e direito à medida que$x$ se aproxima de 2.

Limite esquerdo:$\lim \limits_{x \to 2^−} (x+1)=2+1=3$. O limite esquerdo existe.

Limite à direita:$\lim \limits_{x \to 2^+} (−x)=−2$. O limite à direita existe. Mas

\[\lim \limits_{x \to 2^−} f(x)≠ \lim \limits_{x \to 2^+} f(x).\]

Portanto,$\lim \limits_{x \to 2} f(x)$ não existe e a Condição 2 falha: não há descontinuidade removível. No entanto, como os limites esquerdo e direito existem, mas não são iguais, as condições são satisfeitas para uma descontinuidade do salto em$x=2$.

Exercício$\PageIndex{1}$:

Identifique todas as descontinuidades das seguintes funções como um salto ou uma descontinuidade removível.

$f(x)=\frac{x^2−6x}{x−6}$
$g(x)= \begin{cases} \sqrt{x}, & 0≤x<4 \\ 2x, & x≥4 \end{cases} $

descontinuidade removível em$x=6$;
pule a descontinuidade em$x=4$

Reconhecendo funções contínuas e descontínuas de números reais

Muitas das funções que encontramos nos capítulos anteriores são contínuas em todos os lugares. Eles nunca têm um buraco e nunca saltam de um valor para o outro. Para todas essas funções, o limite de$f(x)$ as$x$ se aproxima de a é o mesmo que o valor de$f(x)$ quando$x=a$. Então$\lim \limits_{x \to a} f(x)=f(a)$. Existem algumas funções que são contínuas em todos os lugares e outras que são contínuas apenas quando são definidas em seu domínio porque não estão definidas para todos os números reais.

EXEMPLOS DE FUNÇÕES CONTÍNUAS

As seguintes funções são contínuas em todos os lugares:

Funções polinomiais	Ex:$f(x)=x^4−9x^2$
Funções exponenciais	Ex:$f(x)=4^{x+2}−5$
Funções senoidais	Ex:$f(x)=\sin (2x)−4$
Funções do cosseno	Ex:$f(x)=− \cos (x+\frac{π}{3})$

As funções a seguir são contínuas em todos os lugares em que estão definidas em seu domínio:

Funções logarítmicas	Ex:$f(x)=2 \ln (x), x>0$
Funções tangentes	Ex:$f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k$ é um número inteiro
Funções racionais	Ex:$f(x)=\frac{x^2−25}{x−7}, x≠7$

como fazer:dada uma função$f(x)$, determine if the function is continuous at $x=a$.

Condição de verificação 1:$f(a)$ existe.
Condição de verificação 2:$\lim \limits_{x \to a} f(x)$ existe em$x=a$.
Verifique a condição 3:$\lim \limits_{x \to a} f(x)=f(a).$
Se todas as três condições forem satisfeitas, a função será contínua em$x=a$. Se alguma das condições não for satisfeita, a função não será contínua em$x=a$.

Exemplo$\PageIndex{2}$: Determining Whether a Piecewise Function is Continuous at a Given Number

Determine se a função$f(x)= \begin{cases} 4x, & x≤3 \\ 8+x, & x>3 \end{cases}$ é contínua em

$x=3$
$x=\frac{8}{3}$

Para determinar se a função$f$ é contínua em,$x=a,$ determinaremos se as três condições de continuidade são satisfeitas em$x=a$.

Condição 1:$f(a)$ Existe?
\[\begin{align} f(3)=4(3)=12 \\ ⇒ \text{Condition 1 is satisfied.} \end{align} \]

Condição 2:$\lim \limits_{x \to 3} f(x)$ Existe?

À esquerda da$x=3, f(x)=4x;$ direita de$x=3, f(x)=8+x.$ Precisamos avaliar os limites esquerdo e direito à medida que$x$ se aproxima de 1.
- Limite esquerdo:$\lim \limits_{x \to 3^−} f(x)= \lim \limits_{x \to 3^−} 4(3)=12$
- Limite à direita:$\lim \limits_{x \to 3^+} f(x)= \lim \limits_{x \to 3^+}(8+x)=8+3=11$
Porque$\lim \limits_{x \to 1^−} f(x)≠ \lim \limits_{x \to 1^+} f(x), \lim \limits_{x \to 1} f(x)$ não existe.

\[⇒ \text{Condition 2 fails.}\]

Não há necessidade de prosseguir. A condição 2 falha em$x=3$. Se alguma das condições de continuidade não for satisfeita em$x=3$, a função não$f(x)$ será contínua em$x=3$.
$x=\frac{8}{3}$
Condição 1:$f(\frac{8}{3})$ Existe?

\[\begin{align} f(\frac{8}{3})=4(\frac{8}{3})=\frac{32}{3} \\ ⇒\text{Condition 1 is satisfied.} \end{align}\]

Condição 2:$\lim \limits_{x \to \frac{8}{3}} f(x)$ Existe?

À esquerda de$x=\frac{8}{3}$,$f(x)=4x$; à direita de$x=\frac{8}{3}, f(x)=8+x$. Precisamos avaliar os limites esquerdo e direito à medida que$x$ se aproximam$\frac{8}{3}$.
- Limite esquerdo:$\lim \limits_{x \to \frac{8}{3}^−} f(x)= \lim \limits_{x \to \frac{8}{3}^−} 4(\frac{8}{3})=\frac{32}{3}$
- Limite à direita:$\lim \limits_{x \to \frac{8}{3}^+} f(x)= \lim \limits_{x \to \frac{8}{3}^+} (8+x)=8+\frac{8}{3}=\frac{32}{3}$
Porque$\lim \limits_{x \to \frac{8}{3}} f(x)$ existe,

\[⇒ \text{Condition 2 is satisfied.}\]

Condição 3: É$f(\frac{8}{3})=\lim \limits_{x \to \frac{8}{3}} f(x)$?

\[\begin{align} f(\frac{32}{3})=\frac{32}{3}=\lim \limits_{x \to \frac{8}{3}} f(x) \\ ⇒ \text{Condition 3 is satisfied.} \end{align}\]

Como todas as três condições de continuidade são satisfeitas em$x=\frac{8}{3}$, a função$f(x)$ é contínua em$x=\frac{8}{3}$.

Exercício$\PageIndex{2}$:

Determine se a função$f(x)= \begin{cases} & \frac{1}{x}, && x≤2 \\ & 9x−11.5, && x>2 \end{cases}$ é contínua em$x=2$.

sim

Exemplo$\PageIndex{3}$: Determining Whether a Rational Function is Continuous at a Given Number

Determine se a função$f(x)=\frac{x^2−25}{x−5}$ é contínua em$x=5$.

Para determinar se a função$f$ é contínua em$x=5$, determinaremos se as três condições de continuidade são satisfeitas em$x=5$.

Condição 1:

\[\begin{align} f(5) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

Não há necessidade de prosseguir. A condição 2 falha em$x=5$. Se alguma das condições de continuidade não for satisfeita em$x=5$, a função f f não é contínua em$x=5$.

Análise

Veja a Figura. Observe que, para a Condição 2, temos

\[\begin{align} \lim \limits_{x \to 5} \dfrac{x^2−25}{x−5} &= \lim \limits_{x \to 3} \dfrac{\cancel{(x−5)}(x+5)}{\cancel{x−5}} \\ &= \lim \limits_{x \to 5}(x+5) \\ &=5+5=10 \\ &⇒ \text{Condition 2 is satisfied.} \end{align}\]

Em x=5, x=5, existe uma descontinuidade removível. Veja a Figura.

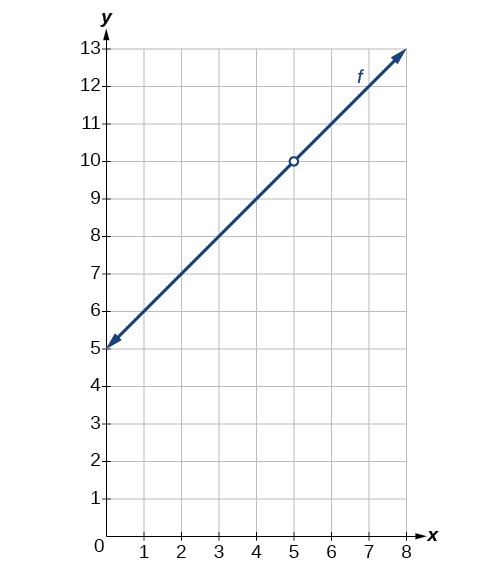
$CNX_Precalc_Figure_12_03_013.jpg$

Exercício$\PageIndex{3}$:

Determine se a função$f(x)=\frac{9−x^2}{x^2−3x}$ é contínua em$x=3$. Caso contrário, indique o tipo de descontinuidade.

Não, a função não é contínua em$x=3$. Existe uma descontinuidade removível em$x=3$.

Determinando os valores de entrada para os quais uma função é descontínua

Agora que podemos identificar funções contínuas, descontinuidades de salto e descontinuidades removíveis, examinaremos funções mais complexas para encontrar descontinuidades. Aqui, analisaremos uma função por partes para determinar se existe algum número real onde a função não é contínua. Uma função por partes pode ter descontinuidades nos pontos limite da função, bem como dentro das funções que a compõem.

Para determinar os números reais para os quais uma função por partes composta por funções polinomiais não é contínua, lembre-se de que as próprias funções polinomiais são contínuas no conjunto de números reais. Qualquer descontinuidade estaria nos pontos limite. Portanto, precisamos explorar as três condições de continuidade nos pontos limite da função por partes.

como: Dada uma função por partes, determine se ela é contínua nos pontos limite

Para cada ponto limite$a$ da função por partes, determine os limites esquerdo e direito como$x$ abordagens, bem$a, $ como o valor da função em$a$.
Verifique cada condição para cada valor para determinar se todas as três condições estão satisfeitas.
Determine se cada valor satisfaz a condição 1:$f(a)$ existe.
Determine se cada valor satisfaz a condição 2:$\lim \limits_{x \to a} f(x)$ existe.
Determine se cada valor satisfaz a condição 3:$\lim \limits_{x \to a} f(x)=f(a).$
Se todas as três condições forem satisfeitas, a função será contínua em$x=a$. Se alguma das condições falhar, a função não será contínua em$x=a$.

Exemplo$\PageIndex{4}$: Determining the Input Values for Which a Piecewise Function Is Discontinuous

Determine se a função f f é descontínua para qualquer número real.

\[fx= \begin{cases} x+1, &x<2 \\ 3, &2≤x<4 \\ x^2−11, & x≥4 \end{cases} \]

Análise

Veja a Figura. Em$x=4$, existe uma descontinuidade de salto. Observe que a função é contínua em$x=2$.

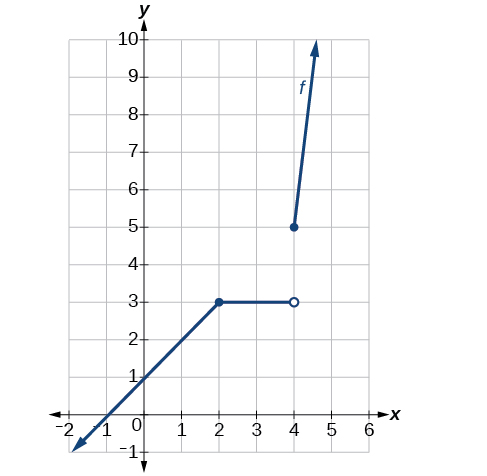
Gráfico de uma função por partes que tem disconuidade em (4, 3).

Exercício$\PageIndex{4}$:

Determine onde a função$f(x)= \begin{cases} \frac{πx}{4}, &x<2 \\ \frac{π}{x}, & 2≤x≤6 \\ 2πx, &x>6 \end{cases}$ é descontínua.

$x=6$

Determinando se uma função é contínua

Para determinar se uma função por partes é contínua ou descontínua, além de verificar os pontos limite, também devemos verificar se cada uma das funções que compõem a função por partes é contínua.

como: Dada uma função por partes, determine se ela é contínua.

Determine se cada função componente da função por partes é contínua. Se houver descontinuidades, elas ocorrem dentro do domínio em que a função do componente é aplicada?
Para cada ponto limite$x=a$ da função por partes, determine se cada uma das três condições é válida.

Exemplo$\PageIndex{5}$: Determining Whether a Piecewise Function Is Continuous

Determine se a função abaixo é contínua. Caso contrário, indique a localização e o tipo de cada descontinuidade.

\[fx= \begin{cases} \sin (x), &x<0 \\ x^3, & x>0 \end{cases}\]

As duas funções que compõem essa função por partes estão$f(x)=\sin (x)$ ativadas$x<0$ e$f(x)=x^3$ ativadas$x>0$. A função seno e todas as funções polinomiais são contínuas em todos os lugares. Quaisquer descontinuidades estariam no ponto limite,

Em$x=0$, vamos verificar as três condições de continuidade.

Condição 1:

\[ \begin{align} f(0) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

Como todas as três condições não são satisfeitas$x=0$, a função$f(x)$ é descontínua em$x=0$.

Análise

Veja a Figura. Existe uma descontinuidade removível em$x=0$;$\lim \limits_{x \to 0} f(x)=0$, portanto, o limite existe e é finito, mas$f(a)$ não existe.

A função tem descontinuidade removível em 0.

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com continuidade.

Conceitos-chave

Uma função contínua pode ser representada por um gráfico sem furos ou quebras.
Uma função cujo gráfico tem furos é uma função descontínua.
Uma função é contínua em um número específico se três condições forem atendidas:
- Condição 1:$f(a)$ existe.
- Condição 2:$\lim \limits_{x \to a} f(x)$ existe em$x=a$.
- Condição 3:$\lim \limits_{x \to a} f(x)=f(a)$.
Uma função tem uma descontinuidade de salto se os limites esquerdo e direito forem diferentes, fazendo com que o gráfico “salte”.
Uma função tem uma descontinuidade removível se puder ser redefinida em seu ponto descontínuo para torná-la contínua. Veja o exemplo.
Algumas funções, como funções polinomiais, são contínuas em todos os lugares. Outras funções, como funções logarítmicas, são contínuas em seu domínio. Veja o exemplo e o exemplo.
Para que uma função por partes seja contínua, cada peça deve ser contínua em sua parte do domínio e a função como um todo deve ser contínua nos limites. Veja o exemplo e o exemplo.

Glossário

função contínua: uma função que não tem furos ou quebras em seu gráfico

função descontínua: uma função que não é contínua em$x=a$

descontinuidade do salto: um ponto de descontinuidade em uma função$f(x)$ em$x=a$ que existem os limites esquerdo e direito, mas$\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

descontinuidade removível: um ponto de descontinuidade em uma função em$f(x)$ que a função é descontínua, mas pode ser redefinida para torná-la contínua

Funções polinomiais	Ex:\(f(x)=x^4−9x^2\)
Funções exponenciais	Ex:\(f(x)=4^{x+2}−5\)
Funções senoidais	Ex:\(f(x)=\sin (2x)−4\)
Funções do cosseno	Ex:\(f(x)=− \cos (x+\frac{π}{3})\)

Funções logarítmicas	Ex:\(f(x)=2 \ln (x), x>0\)
Funções tangentes	Ex:\(f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k\) é um número inteiro
Funções racionais	Ex:\(f(x)=\frac{x^2−25}{x−7}, x≠7\)