12.4: Derivativos
- Page ID
- 189256
O adolescente médio nos Estados Unidos abre uma porta de geladeira cerca de 25 vezes por dia. Supostamente, essa média aumentou em relação a 10 anos atrás, quando o adolescente médio abria a porta da geladeira 20 vezes por dia 1. Estima-se que a televisão esteja ligada em uma casa 6,75 horas por dia, enquanto os pais gastam cerca de 5,5 minutos por dia tendo uma conversa significativa com seus filhos. Essas médias também não são as mesmas de 10 anos atrás, quando a televisão estava ligada cerca de 6 horas por dia em uma casa típica, e os pais passavam 12 minutos por dia em uma conversa significativa com seus filhos. O que esses cenários têm em comum? As funções que os representam mudaram com o tempo. Nesta seção, consideraremos os métodos de computar essas mudanças ao longo do tempo.
Encontrando a taxa média de variação de uma função
As funções que descrevem os exemplos acima envolvem uma mudança ao longo do tempo. A mudança dividida pelo tempo é um exemplo de taxa. As taxas de variação nos exemplos anteriores são diferentes. Em outras palavras, alguns mudaram mais rápido do que outros. Se fôssemos representar graficamente as funções, poderíamos comparar as taxas determinando as inclinações dos gráficos.
Uma reta tangente a uma curva é uma linha que cruza a curva em apenas um único ponto, mas não a cruza lá. (A reta tangente pode cruzar a curva em outro ponto distante do ponto de interesse.) Se ampliarmos uma curva nesse ponto, a curva aparece linear e a inclinação da curva nesse ponto está próxima da inclinação da reta tangente nesse ponto.
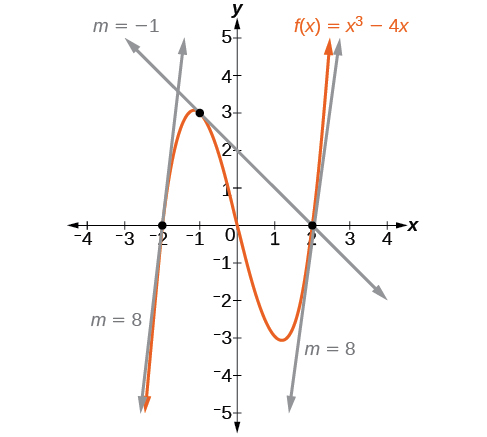
A figura\(\PageIndex{1}\) representa a função\(f(x)=x^3−4x\). Podemos ver a inclinação em vários pontos ao longo da curva.
- inclinação em\(x=−2\) é 8
- inclinação em\(x=−1\) é —1
- inclinação em\(x=2\) é 8
Vamos imaginar um ponto na curva da função\(f\) em,\(x=a\) conforme mostrado na Figura\(\PageIndex{1}\). As coordenadas do ponto são\((a,f(a))\). Conecte esse ponto com um segundo ponto na curva um pouco à direita\(x=a\), com um valor x aumentado em algum pequeno número real\(h\). As coordenadas desse segundo ponto são\((a+h,f(a+h))\) para algum valor positivo\(h\).
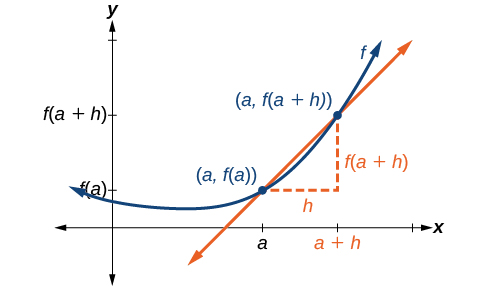
Podemos calcular a inclinação da linha conectando os dois pontos\((a,f(a))\) e\((a+h,f(a+h))\), chamada de linha secante, aplicando a fórmula da inclinação,
\[ \mathrm{slope = \dfrac{change \; in \; y}{change \; in \; x}} \]
Usamos a notação\(m_{sec}\) para representar a inclinação da linha secante conectando dois pontos.
\[\begin{align} m_{sec} &= \dfrac{f(a+h)−f(a)}{(a+h)−(a) } \\ &= \dfrac{f(a+h)−f(a)}{\cancel{a}+h−\cancel{a}} \end{align}\]
A inclinação\(m_{sec}\) é igual à taxa média de variação entre dois pontos\((a,f(a))\) e\((a+h,f(a+h)).\)
\[m_{sec}=\dfrac{f(a+h)−f(a)}{h}\]
A TAXA MÉDIA DE VARIAÇÃO ENTRE DOIS PONTOS EM UMA CURVA
A taxa média de variação (AROC) entre dois pontos\((a,f(a))\) e\((a+h,f(a+h))\) na curva de\(f\) é a inclinação da linha que liga os dois pontos e é dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Exemplo\(\PageIndex{1}\): Finding the Average Rate of Change
Encontre a taxa média de variação conectando os pontos\((2,−6)\)\((−1,5)\) e.
Solução
Sabemos que a taxa média de mudança conectando dois pontos pode ser dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Se um ponto for\((2,−6)\), ou\((2,f(2))\), então\(f(2)=−6.\)
O valor\(h\) é o deslocamento de\(2\) para\(−1\), que é igual a\(−1−2=−3.\)
Para o outro ponto,\(f(a+h)\) é a coordenada y em\(a+h\), que é mais\(2+(−3)\) ou\(−1,\) menos\(f(a+h)=f(−1)=5\).
\[\begin{align} \text{AROC} &= \dfrac{f(a+h)−f(a)}{h} \\ &=\dfrac{5−(−6)}{−3} \\&=\dfrac{11}{−3} \\ &=−\dfrac{11}{3} \end{align}\]
Exercício\(\PageIndex{1}\)
Encontre a taxa média de variação conectando os pontos\((−5,1.5)\) e\((−2.5,9)\)
Solução
3
Entendendo a taxa instantânea de mudança
Agora que podemos encontrar a taxa média de variação, suponha que façamos\(h\) na Figura\(\PageIndex{2}\) cada vez menor. Em seguida, se\(a+h\) aproximará\(a\) à medida\(h\) que fica menor, ficando cada vez mais perto de 0. Da mesma forma, o segundo ponto\((a+h,f(a+h))\) se aproximará do primeiro ponto,\((a,f(a))\). Como consequência, a linha de conexão entre os dois pontos, chamada linha secante, ficará cada vez mais perto de ser uma tangente à função at\(x=a\), e a inclinação da linha secante se aproximará cada vez mais da inclinação da tangente em\(x=a\) (Figura\(\PageIndex{3}\)).
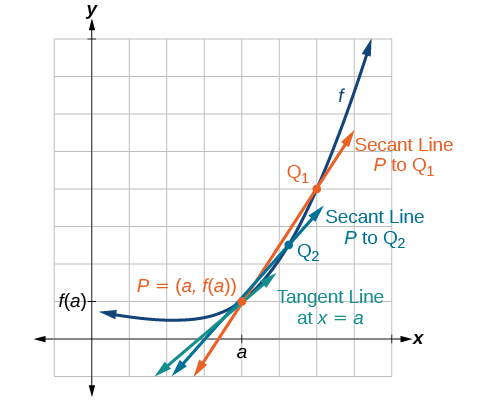
Como estamos procurando a inclinação da tangente em\(x=a\), podemos pensar na medida da inclinação da curva de uma função\(f\) em um determinado ponto como a taxa de variação em um determinado instante. Chamamos essa inclinação de taxa instantânea de mudança, ou a derivada da função em\(x=a.\) Ambos pode ser encontrada encontrando o limite da inclinação de uma linha conectando o ponto a\(x=a\) com um segundo ponto infinitesimalmente próximo ao longo da curva. Para uma função,\(f\) tanto a taxa instantânea de mudança da função quanto a derivada da função at\(x=a\) são escritas como\(f'(a),\) e podemos defini-las como um limite bilateral que tem o mesmo valor, seja abordado pela esquerda ou pela direita.
\[f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
A expressão pela qual o limite é encontrado é conhecida como quociente de diferença.
DEFINIÇÃO DE TAXA INSTANTÂNEA DE VARIAÇÃO E DERIVADA
A derivada, ou taxa instantânea de variação, de uma função\(f\) em\(x=a\), é dada por
\[ f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
A expressão\(\frac{f(a+h)−f(a)}{h}\) é chamada de quociente de diferença.
Usamos o quociente de diferença para avaliar o limite da taxa de variação da função à medida que\(h\) se aproxima de 0.
Derivadas: Interpretações e notação
A derivada de uma função pode ser interpretada de maneiras diferentes. Pode ser observado como o comportamento de um gráfico da função ou calculado como uma taxa numérica de variação da função.
- A derivada de uma função\(f(x)\) em um ponto\(x=a\) é a inclinação da reta tangente à curva\(f(x)\) em\(x=a\). A derivada de\(f(x)\) at\(x=a\) é escrita\(f′(a)\).
- A derivada\(f′(a)\) mede como a curva muda no ponto\((a,f(a))\).
- A derivada\(f′(a)\) pode ser considerada como a taxa instantânea de mudança da função\(f(x)\) em\(x=a\).
- Se uma função mede a distância em função do tempo, a derivada mede a velocidade instantânea no tempo\(t=a\).
NOTAÇÕES PARA A DERIVADA
A equação da derivada de uma função\(f(x)\) é escrita como\(y′=f′(x)\), onde\(y=f(x)\). A notação\(f′(x)\) é lida como “\(f\)primo de”\(x\). As notações alternativas para a derivada incluem o seguinte:
\[f′(x)=y′=\dfrac{dy}{dx}=\dfrac{df}{dx}=\dfrac{d}{dx} f(x)=Df(x)\]
A expressão agora\(f′(x)\) é uma função de\(x\); essa função fornece a inclinação da curva\(y=f(x)\) em qualquer valor de\(x\). A derivada de uma função\(f(x)\) em um ponto\(x=a\) é indicada\(f′(a)\).
como: Dada uma função\(f\), find the derivative by applying the definition of the derivative.
- Calcular\(f(a+h)\).
- Calcular\(f(a)\).
- Substitua e simplifique\(\frac{f(a+h)−f(a)}{h}\).
- Avalie o limite se ele existir:\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
Exemplo\(\PageIndex{1}\): Finding the Derivative of a Polynomial Function
Encontre a derivada da função\(f(x)=x^2−3x+5\) em\(x=a.\)
Solução
Nós temos:
\[ f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \;\;\;\;\;\;\;\; \text{Definition of a derivative}\]
Substituir\(f(a+h)=(a+h)^2−3(a+h)+5\) e\(f(a)=a^2−3a+5.\)
\[ \begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{(a+h)(a+h)−3(a+h)+5−(a^2−3a+5)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−3a−3h+5−a^2+3a−5}{h} && \text{Evaluate to remove parentheses.} \\ & = \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{3a}−3h+\cancel{5}−\cancel{a^2}+\cancel{3a}−\cancel{5}}{h} && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \dfrac{2ah+h^2−3h}{h} && \text{Factor out an }h. \\ & =2a+0−3 && \text{Evaluate the limit.} \\ &=2a−3 \end{align} \]
Exercício\(\PageIndex{1}\)
Encontre a derivada da função\(f(x)=3x^2+7x\) em\(x=a\)
Solução
\(f′(a)=6a+7\)
Encontrando derivadas de funções racionais
Para encontrar a derivada de uma função racional, às vezes simplificamos a expressão usando técnicas algébricas que já aprendemos.
Exemplo\(\PageIndex{1}\): Finding the Derivative of a Rational Function
Encontre a derivada da função\(f(x)=\dfrac{3+x}{2−x}\) em\(x=a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a})}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \\ &= \lim \limits_{h \to 0} \dfrac{(2−(a+h))(2−a)[ \frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a}) ]}{(2−(a+h))(2−a)(h)} && \text{Multiply numerator and denominator by } (2−(a+h))(2−a) \\ & =\lim \limits_{h \to 0}\dfrac{(\cancel{2−(a+h)})(2−a)(\frac{3+(a+h)}{\cancel{(2−(a+h))}})−(2−(a+h))\cancel{(2−a)}(\frac{3+a}{\cancel{2−a}})}{(2−(a+h))(2−a)(h)} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{6−3a+2a−a^2+2h−ah−6+3a+3h−2a+a^2+ah}{(2−(a+h))(2−a)(h)} && \text{Multiply} \\ &=\lim \limits_{h \to 0} \dfrac{5 \cancel{h}}{(2−(a+h))(2−a)(\cancel{h})} && \text{Combine like terms} \\ & = \lim \limits_{h \to 0} \dfrac{5}{(2−(a+h))(2−a)} && \text{Cancel like factors} \\ & =\dfrac{5}{(2−(a+0))(2−a)}=\dfrac{5}{(2−a)(2−a)}=\dfrac{5}{(2−a)^2} && \text{Evaluate the limit} \end{align}\]
Exercício\(\PageIndex{1}\):
Encontre a derivada da função\(f(x)=\frac{10x+11}{5x+4}\) em\(x=a\).
\[f′(a)=\dfrac{−15}{(5a+4)^2}\]
Encontrando derivadas de funções com raízes
Para encontrar derivadas de funções com raízes, usamos os métodos que aprendemos para encontrar limites de funções com raízes, incluindo a multiplicação por um conjugado.
Exemplo\(\PageIndex{1}\): Finding the Derivative of a Function with a Root
Encontre a derivada da função\(f(x)=4\sqrt{x}\) em\(x=36.\)
Nós temos
\[\begin{align} f′(a) &=\lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \end{align}\]
Multiplique o numerador e o denominador pelo conjugado:\(\frac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}}\).
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\bigg( \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} \bigg)⋅ \bigg(\dfrac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}} \bigg) \\ &=\lim \limits_{h \to 0} \bigg( \dfrac{16(a+h)−16a}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Multiply.} \\ &=\lim \limits_{ h \to 0} \bigg( \dfrac{\cancel{16a}+16h\cancel{−16a}}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Distribute and combine like terms.} \\ &= \lim \limits_{h \to 0}\bigg(\dfrac{16\cancel{h}}{\cancel{h}(4\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \bigg( \dfrac{16}{4\sqrt{a+h}+4\sqrt{a}} \bigg) && \text{Evaluate the limit by letting } h=0. \\ & =\dfrac{16}{8\sqrt{a}}=\dfrac{2}{\sqrt{a}} \\ f′(36) &= \dfrac{2}{\sqrt{36}} && \text{Evaluate the derivative at } x=36. \\ &=\dfrac{2}{6} \\ & =\dfrac{1}{3} \end{align}\]
Exercício\(\PageIndex{1}\):
Encontre a derivada da função\(f(x)=9\sqrt{x}\) em\(x=9.\)
\(\frac{3}{2}\)
Encontrando taxas de mudança instantâneas
Muitas aplicações da derivada envolvem determinar a taxa de variação em um determinado instante de uma função com a variável independente tempo, razão pela qual o termo instantâneo é usado. Considere a altura de uma bola lançada para cima com uma velocidade inicial de 64 pés por segundo, dada por\(s(t)=−16t^2+64t+6\), onde\(t\) é medida em segundos e\(s(t)\) é medida em pés. Sabemos que o caminho é o de uma parábola. A derivada nos dirá como a altura está mudando em um determinado momento. A altura da bola é mostrada na Figura em função do tempo. Em física, chamamos isso de “grafo s - t”.
Exemplo\(\PageIndex{1}\): Finding the Instantaneous Rate of Change
Usando a função acima\(s(t)=−16t^2+64t+6\),, qual é a velocidade instantânea da bola em 1 segundo e 3 segundos de seu voo?
A velocidade em\(t=1\) e\(t=3\) é a taxa instantânea de mudança de distância por tempo, ou velocidade. Observe que a altura inicial é de 6 pés. Para encontrar a velocidade instantânea, encontramos a derivada e a calculamos em\(t=1\) e\(t=3\):
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(t+h)^2+64(t+h)+6−(−16t^2+64t+6)}{h} && \text{Substitute } s(t+h) \text{ and } s(t). \\ &= \lim \limits_{h \to 0} \dfrac{−16t^2−32ht−h^2+64t+64h+6+16t^2−64t−6}{h} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{−32ht−h^2+64h}{h} && \text{Simplify.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(−32t−h+64)}{\cancel{h}} && \text{Factor the numerator.} \\ & =\lim \limits_{h \to 0}−32t−h+64 && \text{ Cancel out the common factor} h. \\ s′(t) &=−32t+64 && \text{Evaluate the limit by letting} h=0. \end{align}\]
Para qualquer valor de\(t\), nos\(s′(t)\) diz a velocidade nesse valor de\(t\).
Avalie\(t=1\)\(t=3\) e.
\[\begin{align}s′(1) &=−32(1)+64=32 \\ s′(3) &=−32(3)+64=−32 \end{align}\]
A velocidade da bola após 1 segundo é de 32 pés por segundo, enquanto ela está subindo.
A velocidade da bola após 3 segundos é de −32 pés por segundo, já que ela está descendo.
Exercício\(\PageIndex{1}\):
A posição da bola é dada por\(s(t)=−16t^2+64t+6.\) Qual é a velocidade de 2 segundos de voo?
0
Usando gráficos para encontrar taxas de mudança instantâneas
Podemos estimar uma taxa instantânea de mudança em\(x=a\) observando a inclinação da curva da função\(f(x)\) em\(x=a\). Fazemos isso desenhando uma linha tangente à função at\(x=a\) e encontrando sua inclinação.
como: Dado um gráfico de uma função\(f( x )\), find the instantaneous rate of change of the function at \(x=a\).
- Localize\(x=a\) no gráfico da função\(f(x)\).
- Desenhe uma reta tangente, uma linha que passa\(x=a\) em\(a\) nenhum outro ponto dessa seção da curva. Estenda a linha o suficiente para calcular sua inclinação como
\[\dfrac{\text{change in }y}{\text{change in }x.}\]
Exemplo\(\PageIndex{1}\): Estimating the Derivative at a Point on the Graph of a Function
A partir do gráfico da função\(y=f(x)\) apresentado na Figura, estime cada um dos seguintes:
\(f(0) ; f(2) ; f'(0) ; f'(2)\)
Para encontrar o valor funcional\(f(a)\), encontre a coordenada y em\(x=a\).
Para encontrar a derivada em,\(x=a, f′(a),\) desenhe uma reta tangente em\(x=a,\) e estime a inclinação dessa reta tangente. Veja a Figura.
- \(f(0)\)é a coordenada y em\(x=0\). O ponto tem coordenadas\((0,1)\), portanto\(f(0)=1\).
- \(f(2)\)é a coordenada y em\(x=2\). O ponto tem coordenadas\((2,1)\), portanto\(f(2)=1\).
- \(f′(0)\)é encontrado estimando a inclinação da reta tangente à curva em\(x=0\). A linha tangente à curva em\(x=0\) aparece na horizontal. As linhas horizontais têm uma inclinação de 0, portanto\(f′(0)=0\).
- \(f′(2)\)é encontrado estimando a inclinação da reta tangente à curva em\(x=2\). Observe o caminho da reta tangente à curva em\(x=2\). À medida que o\(x\) valor move uma unidade para a direita, o\(y\) valor sobe quatro unidades até outro ponto na linha. Assim, a inclinação é 4, então\(f′(2)=4\).
Exercício\(\PageIndex{1}\):
Usando o gráfico da função\(f(x)=x^3−3x\) mostrado na Figura, estime:\(f(1), f′(1), f(0)\),\(f′(0)\) e.
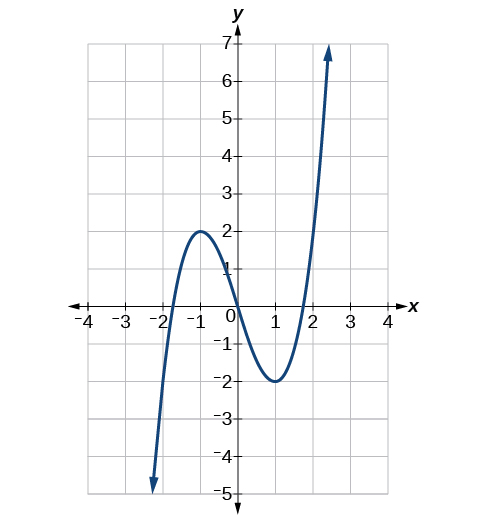
−2, −2,0, 0, −3
Usando taxas instantâneas de mudança para resolver problemas do mundo real
Outra forma de interpretar uma taxa instantânea de mudança em\(x=a\) é observar a função em um contexto do mundo real. A unidade para a derivada de uma função\(f(x)\) é
\[\dfrac{\text{output units}}{\text{input unit}}\]
Essa unidade mostra por quantas unidades a saída muda para cada mudança de entrada de uma unidade. A taxa instantânea de variação em um determinado instante mostra a mesma coisa: as unidades de variação de saída por mudança de entrada de uma unidade.
Um exemplo de taxa de variação instantânea é um custo marginal. Por exemplo, suponha que o custo de produção de uma empresa para produzir\(x\) itens seja dado\(C(x)\) em milhares de dólares. A função derivada nos diz como o custo está mudando para qualquer valor de\(x\) no domínio da função. Em outras palavras,\(C′(x)\) é interpretado como um custo marginal, o custo adicional em milhares de dólares de produzir mais um item quando\(x\) os itens foram produzidos. Por exemplo,\(C′(11)\) é o custo adicional aproximado em milhares de dólares da produção do 12º item após 11 itens terem sido produzidos. \(C′(11)=2.50\)significa que, quando 11 itens forem produzidos, produzir o 12º item aumentaria o custo total em aproximadamente $2.500,00.
Exemplo\(\PageIndex{1}\): Finding a Marginal Cost
O custo em dólares da produção de\(x\) laptops em dólares é\(f(x)=x^2−100x.\) No ponto em que 200 computadores foram produzidos, qual é o custo aproximado de produzir a 201 unidade?
Se\(f(x)=x^2−100x\) descreve o custo de produção de\(x\) computadores,\(f′(x)\) descreverá o custo marginal. Precisamos encontrar a derivada. Para fins de cálculo da derivada, podemos usar as seguintes funções:
\[\begin{align} f(a+b) &=(x+h)^2−100(x+h) \\ f(a) &=a ^2−100a \end{align}\]
\[\begin{align} f′(x) &=\dfrac{f(a+h)−f(a)}{h} && \text{Formula for a derivative} \\ &=\dfrac{(x+h)^2−100(x+h)−(x^2−100x)}{h} \\ \text{Substitute }f(a+h) \text{ and }f(a). \\ & =\dfrac{x^2+2xh+h^2−100x−100h−x^2+100x}{h} && \text{Multiply polynomials, distribute.} \\ &= \text{2xh+h^2−100h}{h} && \text{Collect like terms.} \\ &=\dfrac{\cancel{h}(2x+h−100)}{\cancel{h}} && \text{Factor and cancel like terms.} \\ &=2x+h−100 && \text{Simplify.} \\ &=2x−100 && \text{Evaluate when }h=0. \\ f′(x) &=2x−100 && \text{Formula for marginal cost} \\ f′(200) &=2(200)−100=300 && \text{Evaluate for 200 units.} \end{align}\]
O custo marginal de produção da 201 unidade será de aproximadamente $300.
Exemplo\(\PageIndex{1}\):Interpreting a Derivative in Context
Um carro sai de um cruzamento. A distância percorrida em milhas é dada pela função\( f(t)\), onde\(t\) representa horas. Explique as seguintes notações:
\(f(0)=0 f′(1)=60 f(1)=70 f(2.5)=150\)
Primeiro, precisamos avaliar a função\(f(t)\) e a derivada da função\(f′(t)\) e distinguir entre as duas. Quando avaliamos a função\(f(t)\), estamos encontrando a distância percorrida pelo carro em\(t\) horas. Quando avaliamos a derivada f (t), f (t), estamos encontrando a velocidade do carro após\(t\) horas.
- \(f(0)=0\)significa que em zero horas, o carro percorreu zero milhas.
- \(f′(1)=60\)significa que uma hora após o início da viagem, o carro está viajando 60 milhas por hora.
- \(f(1)=70\)significa que após uma hora de viagem, o carro viajou 70 milhas. Em algum momento durante a primeira hora, então, o carro deve ter viajado mais rápido do que estava na marca de 1 hora.
- \(f(2.5)=150\)significa que duas horas e trinta minutos após o início da viagem, o carro viajou 150 milhas.
Exercício\(\PageIndex{1}\)
Um corredor corre por uma estrada reta leste-oeste. A função\(f(t)\) indica quantos metros a leste do ponto de partida ela está após\(t\) alguns segundos. Interprete cada um dos itens a seguir no que se refere ao corredor.
\(f(0)=0 ; f(10)=150 ; f′(10)=15 ; f′(20)=−10 ; f(40)=−100\)
- Depois de zero segundos, ela viajou 0 pés.
- Depois de 10 segundos, ela viajou 150 pés para o leste.
- Depois de 10 segundos, ela está se movendo para o leste a uma taxa de 15 pés/seg.
- Depois de 20 segundos, ela está se movendo para o oeste a uma taxa de 10 pés/seg.
- Depois de 40 segundos, ela está 100 pés a oeste de seu ponto de partida.
Encontrando pontos em que a derivada de uma função não existe
Para entender onde a derivada de uma função não existe, precisamos lembrar o que normalmente acontece quando uma função\(f(x)\) tem uma derivada em\(x=a\). Suponha que usemos um utilitário gráfico para ampliar\(x=a\). Se a função\(f(x)\) for diferenciável, ou seja, se for uma função que pode ser diferenciada, quanto mais se aproxima o zoom, mais próximo o gráfico se aproxima de uma linha reta. Essa característica é chamada de linearidade.
Veja o gráfico na Figura. Quanto mais aproximamos o zoom do ponto, mais linear a curva aparece.
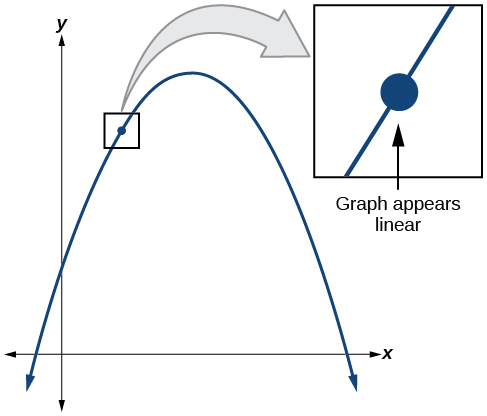
Gráfico da função\(f(x)=| x |\), com eixo x de —0,1 a 0,1 e eixo y de —0,1 a 0,1.
Quais são as características de um gráfico que não é diferenciável em um ponto? Aqui estão alguns exemplos em que a função não\(f(x)\) é diferenciável em\(x=a\).
Na Figura, vemos o gráfico de
\[f(x)=\begin{cases} x^2, &&x≤2 \\ 8−x, &&x>2.\end{cases} .\]
Observe que, à medida que\(x\) se aproxima de 2 pela esquerda, o limite esquerdo pode ser observado como 4, enquanto quando\(x\) se aproxima de 2 da direita, o limite direito pode ser observado como 6. Vemos que tem uma descontinuidade em\(x=2\).
O gráfico de\(f(x)\) tem uma descontinuidade em\(x=2\).
Na Figura, vemos o gráfico de\(f(x)=|x|\). Vemos que o gráfico tem um ponto angular em\(x=0\).
O gráfico de\(f(x)=| x |\) tem um ponto angular em\(x=0\).
Na Figura, vemos que o gráfico de\(f(x)=x^{\frac{2}{3}}\) tem uma cúspide em\(x=0\). Uma cúspide tem uma característica única. Afastando-se da cúspide, os limites esquerdo e direito se aproximam do infinito ou do infinito negativo. Observe que as linhas tangentes à medida que\(x\) se aproximam de 0 da esquerda e da direita parecem ficar cada vez mais íngremes, mas uma tem uma inclinação negativa e a outra tem uma inclinação positiva.
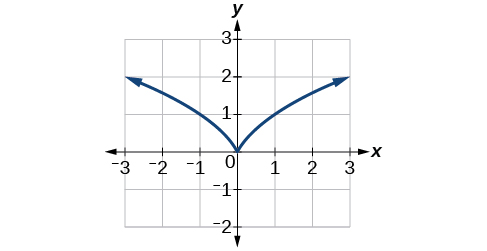
O gráfico de\(f(x)=x^\frac{2}{3}\) tem uma cúspide em\(x=0\).
Na Figura, vemos que o gráfico de\(f(x)=x^{frac{1}{3}}\) tem uma tangente vertical em\(x=0\). Lembre-se de que as tangentes verticais são linhas verticais, então, onde existe uma tangente vertical, a inclinação da linha é indefinida. É por isso que a derivada, que mede a inclinação, não existe lá.

O gráfico de\(f(x)=x^\frac{1}{3}\) tem uma tangente vertical em\(x=0\).
diferenciabilidade
Uma função\(f(x)\) é diferenciável\(x=a\) se a derivada existir em\(x=a\), o que significa que ela\(f′(a)\) existe.
Há quatro casos em que uma função não\(f(x)\) é diferenciável em um determinado ponto\(x=a\).
- Quando há uma descontinuidade em\(x=a\).
- Quando há um ponto angular em\(x=a\).
- Quando há uma cúspide em\(x=a\).
- Qualquer outro momento em que haja uma tangente vertical em\(x=a\).
Exemplo\(\PageIndex{1}\): Determining Where a Function Is Continuous and Differentiable from a Graph
Usando a Figura, determine onde a função está
- contínuo
- descontínuo
- diferenciável
- não diferenciável
Nos pontos em que o gráfico é descontínuo ou não é diferenciável, indique o porquê.
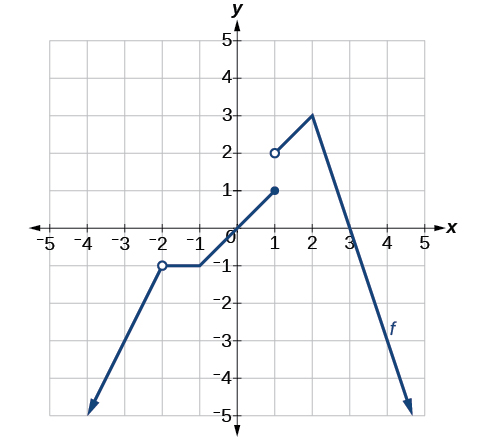
Três intervalos em que a função é contínua
O gráfico de é diferenciável em\((−∞,−2)∪(−2,−1)∪(−1,1)∪(1,2)∪(2,∞)\). O gráfico de não\(f(x)\) é diferenciável\(x=−2\) porque é um ponto de descontinuidade, em\(x=−1\) por causa de um canto agudo, em\(x=1\) porque é um ponto de descontinuidade e em\(x=2\) por causa de um canto agudo. Veja a Figura.
Cinco intervalos em que a função é diferenciável
Exercício\(\PageIndex{1}\):
Determine onde a função\(y=f(x)\) mostrada na Figura é contínua e diferenciável do gráfico.
O gráfico de\(f\) é contínuo em\((−∞,1)∪(1,3)∪(3,∞).\) O gráfico de f f é descontínuo em\(x=1\)\(x=3\) e. O gráfico de\(f\) é diferenciável em\((−∞,1)∪(1,3)∪(3,∞)\). O gráfico de não\(f\) é diferenciável em\(x=1\)\(x=3\) e.
Encontrando uma equação de uma reta tangente ao gráfico de uma função
A equação de uma reta tangente a uma curva da função\(f(x)\) at\(x=a\) é derivada da forma de inclinação pontual de uma linha,\(y=m(x−x_1)+y_1\). A inclinação da reta é a inclinação da curva em\(x=a\) e, portanto, é igual\(f′(a),\) à derivada de\(f(x)\) at\(x=a.\) O par de coordenadas do ponto na linha at\(x=a\) é\((a,f(a))\).
Se substituirmos na forma ponto-inclinação, temos
A equação da reta tangente é
\[y=f'(a)(x−a)+f(a)\]
F
A equação de uma reta tangente à curva de uma função\(f\) em um ponto\(x=a\) é
\[y=f'(a)(x−a)+f(a)\]
como: Dada uma função\(f\), find the equation of a line tangent to the function at \(x=a\).
- Encontre a derivada de\(f(x)\) at\(x=a\) usando\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}.\)
- Avalie a função em\(x=a\). Isso é\(f(a)\).
- Substitua\((a,f(a))\) e\(f′(a)\) entre\(y=f'(a)(x−a)+f(a)\).
- Escreva a equação da reta tangente no formulário\(y=mx+b\).
Exemplo\(\PageIndex{1}\): Finding the Equation of a Line Tangent to a Function at a Point
Encontre a equação de uma reta tangente à curva\(f(x)=x^2−4x\) em\(x=3.\)
Usando:
\[f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Substituir\(f(a+h)=(a+h)^2−4(a+h)\) e\(f(a)=a^2−4a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\dfrac{(a+h)(a+h)−4(a+h)−(a2−4a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−4a−4h−a^2+4a}{h} && \text{Remove parentheses.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{4a}−4h−\cancel{a^2}+\cancel{4a}}{h} && \text{Combine like terms.} \\ &= \lim \limits_{h \to 0} \dfrac{2ah+h^2−4h}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(2a+h−4)}{h} && \text{Factor out }h. \\ &=2a+0−4 \\ f′(a)&=2a−4 && \text{Evaluate the limit.} \\ f′(3)&=2(3)−4=2 \end{align}\]
Equação da reta tangente em\(x=3\):
\[\begin{align} y &= f'(a)(x−a)+f(a) \\ y &=f'(3)(x−3)+f(3) \\ y &=2(x−3)+(−3) \\ y &=2x−9 \end{align}\]
Análise
Podemos usar um utilitário gráfico para representar graficamente a função e a reta tangente. Ao fazer isso, podemos observar o ponto de tangência\(x=3\) conforme mostrado na Figura.
O gráfico confirma o ponto de tangência em\(x=3\).
Exercício\(\PageIndex{1}\):
Encontre a equação de uma reta tangente à curva da função\(f(x)=5x^2−x+4\) em\(x=2\).
\(y=19x−16\)
Encontrando a velocidade instantânea de uma partícula
Se uma função mede a posição versus o tempo, a derivada mede o deslocamento em relação ao tempo ou a velocidade do objeto. Uma mudança na velocidade ou direção em relação a uma mudança no tempo é conhecida como velocidade. A velocidade em um determinado instante é conhecida como velocidade instantânea.
Ao tentar encontrar a velocidade ou a velocidade de um objeto em um determinado instante, parece que encontramos uma contradição. Normalmente definimos velocidade como a distância percorrida dividida pelo tempo decorrido. Mas em um instante, nenhuma distância é percorrida e nenhum tempo passa. Como dividiremos zero por zero? O uso de um derivado resolve esse problema. Uma derivada nos permite dizer que, mesmo que a velocidade do objeto esteja mudando constantemente, ela tem uma certa velocidade em um determinado instante. Isso significa que se o objeto viajasse na velocidade exata por uma unidade de tempo, ele percorreria a distância especificada.
VELOCIDADE INSTANTÂNEA
Deixe a função\(s(t)\) representar a posição de um objeto no momento\(t.\) A velocidade instantânea ou a velocidade do objeto no momento\(t=a\) é dada por
\[s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h}\]
Exemplo\(\PageIndex{1}\): Finding the Instantaneous Velocity
Uma bola é lançada para cima a partir de uma altura de 200 pés com uma velocidade inicial de 36 pés/seg. Se a altura da bola em pés após\(t\) segundos for dada pela\(s(t)=−16t^2+36t+200,\) determinação da velocidade instantânea da bola em\( t=2\).
Primeiro, precisamos encontrar a derivada\(s′(t)\). Em seguida, avaliamos a derivada em\(t=2\), usando\(s(a+h)=−16(a+h)^2+36(a+h)+200\) e\(s(a)=−16a^2+36a+200.\)
\[\begin{align} s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16(a+h)^2+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(a^2+2ah+h^2)+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16a^2−32ah−16h^2+36a+36h+200+16a^2−36a−200}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{−16a^2}−32ah−16h^2+\cancel{36a}+36h+\cancel{200}+\cancel{16a^2}−\cancel{36a}−\cancel{200}}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−32ah−16h^2+36h}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{h}(−32a−16h+36)}{\cancel{h}} \\ &= \lim \limits_{h \to 0}(−32a−16h+36) \\&=−32a−16⋅0+36 \\ s′(a) &=−32a+36 \\ s′(2) &=−32(2)+36 \\ & =−28 \end{align}\]
Análise
Esse resultado significa que, em\(t=2\) segundos, a bola está caindo a uma taxa de 28 pés/seg.
Exercício\(\PageIndex{1}\):
Um foguete de fogos de artifício é lançado para cima de um poço 12 pés abaixo do solo a uma velocidade de 60 pés/seg. Sua altura em pés após\(t\) segundos é dada por\(s=−16t^2+60t−12.\) Qual é sua velocidade instantânea após 4 segundos?
—68 pés/seg, ele está caindo de volta para a Terra a uma taxa de 68 pés/s.
Acesse esses recursos on-line para obter instruções e práticas adicionais com derivados.
Visite este site para obter mais perguntas práticas do Learningpod.
Equações chave
| taxa média de variação | \(\text{AROC}=\frac{f(a+h)−f(a)}{h}\) |
| derivada de uma função | \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\) |
Conceitos chave
- A inclinação da linha secante conectando dois pontos é a taxa média de variação da função entre esses pontos. Veja o exemplo.
- A derivada, ou taxa instantânea de mudança, é uma medida da inclinação da curva de uma função em um determinado ponto, ou da inclinação da reta tangente à curva nesse ponto. Veja exemplo, exemplo e exemplo.
- O quociente de diferença é o quociente na fórmula para a taxa de variação instantânea:
\(\frac{f(a+h)−f(a)}{h}\)
- Taxas instantâneas de mudança podem ser usadas para encontrar soluções para muitos problemas do mundo real. Veja o exemplo.
- A taxa instantânea de mudança pode ser encontrada observando a inclinação de uma função em um ponto em um gráfico desenhando uma linha tangente à função nesse ponto. Veja o exemplo.
- As taxas instantâneas de mudança podem ser interpretadas para descrever situações do mundo real. Veja o exemplo e o exemplo.
- Algumas funções não são diferenciáveis em um ponto ou pontos. Veja o exemplo.
- A forma de inclinação pontual de uma linha pode ser usada para encontrar a equação de uma reta tangente à curva de uma função. Veja o exemplo.
- A velocidade é uma mudança na posição em relação ao tempo. A velocidade instantânea descreve a velocidade de um objeto em um determinado instante. A velocidade média descreve a velocidade mantida em um intervalo de tempo.
- O uso da derivada torna possível calcular a velocidade instantânea, mesmo que não haja tempo decorrido. Veja o exemplo.
Seção Exercícios
Verbal
Como a inclinação de uma função linear é semelhante à derivada?
A inclinação de uma função linear permanece a mesma. A derivada de uma função geral varia de acordo com\(x\). Tanto a inclinação de uma linha quanto a derivada em um ponto medem a taxa de mudança da função.
Qual é a diferença entre a taxa média de mudança de uma função no intervalo\([ x,x+h ]\) e a derivada da função em\(x\)?
Um carro percorreu 110 milhas durante o período das 14h às 16h. Qual foi a velocidade média do carro? Exatamente às 14h30, a velocidade do carro registrou exatamente 62 milhas por hora. Qual é outro nome para a velocidade do carro às 14h30? Por que essa velocidade difere da velocidade média?
A velocidade média é de 55 milhas por hora. A velocidade instantânea às 14h30 é de 62 milhas por hora. A velocidade instantânea mede a velocidade do carro em um instante de tempo, enquanto a velocidade média fornece a velocidade do carro em um intervalo.
Explique o conceito da inclinação de uma curva em um ponto\(x\).
Suponha que a água esteja fluindo para um tanque a uma taxa média de 45 galões por minuto. Traduza essa afirmação para a linguagem da matemática.
A taxa média de variação da quantidade de água no tanque é de 45 galões por minuto. Se\(f(x)\) for a função que fornece a quantidade de água no tanque a qualquer momento\(t\), então a taxa média de variação\(f(x)\) entre\(t=a\) e\(t=b\) é\(f(a)+45(b−a).\)
Algébrico
Para os exercícios a seguir, use a definição de derivada\(\lim \limits_{h to 0} \frac{f(x+h)−f(x)}{h}\) para calcular a derivada de cada função.
\(f(x)=3x−4\)
\(f(x)=−2x+1\)
\(f′(x)=−2\)
\(f(x)=x^2−2x+1\)
\ (f (x) =2x^2+x−3
\(f′(x)=4x+1\)
\(f(x)=2x^2+5\)
\(f(x)=\frac{−1}{x−2}\)
\(f′(x)=\frac{1}{(x−2)^2}\)
\(f(x)=\frac{2+x}{1−x}\)
\(f(x)=\frac{5−2x}{3+2x}\)
\(\frac{−16(}{3+2x)^2}\)
\(f(x)=\sqrt{1+3x}\)
\(f(x)=3x^3−x^2+2x+5\)
\(f′(x)=9x^2−2x+2\)
\(f(x)=5\)
\(f(x)=5π\)
\(f′(x)=0\)
Para os exercícios a seguir, encontre a taxa média de variação entre os dois pontos.
\((−2,0)\)e\((−4,5)\)
\((4,−3)\)e\((−2,−1)\)
\(−\frac{1}{3}\)
\((0,5)\)e\((6,5)\)
\((7,−2)\)e\((7,10)\)
indefinida
Para as seguintes funções polinomiais, encontre as derivadas.
\(f(x)=x^3+1\)
\(f(x)=−3x^2−7x=6\)
\(f′(x)=−6x−7\)
\(f(x)=7x^2\)
\(f(x)=3x^3+2x^2+x−26\)
\(f′(x)=9x^2+4x+1\)
Para as funções a seguir, encontre a equação da reta tangente à curva\(x\) no ponto dado da curva.
\(f(x)=2x^2−3x \;\;\; x=3\)
\(f(x)=x^3+1 \;\;\;\; x=2\)
\(y=12x−15\)
\(f(x)=\sqrt{x} \;\;\;\; x=9\)
Para o exercício a seguir, descubra de\(k\) forma que a linha dada seja tangente ao gráfico da função.
\(f(x)=x^2−kx, \;\;\; y=4x−9\)
\(k=−10\)ou\(k=2\)
Gráfica
Para os exercícios a seguir, considere o gráfico da função\(f\) e determine onde a função é contínua/descontínua e diferenciável/não diferenciável.
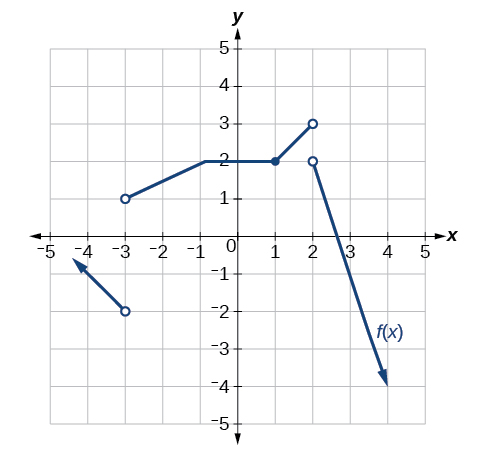
Descontínuo em\(x=−2\)\(x=0\) e. Não é diferenciável em —2, 0, 2.
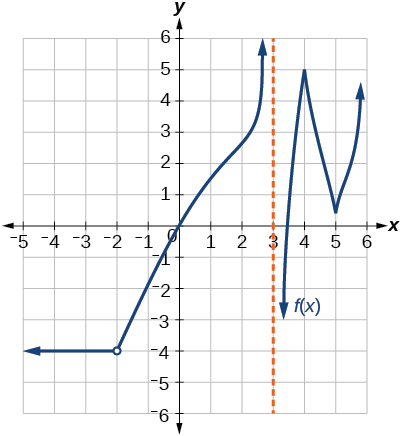
Descontínuo em\(x=5\). Não diferenciável em -4, —2, 0, 1, 3, 4, 5.
Para os exercícios a seguir, use Figura para estimar a função em um determinado valor de\(x\) ou a derivada em um determinado valor de\(x\), conforme indicado.
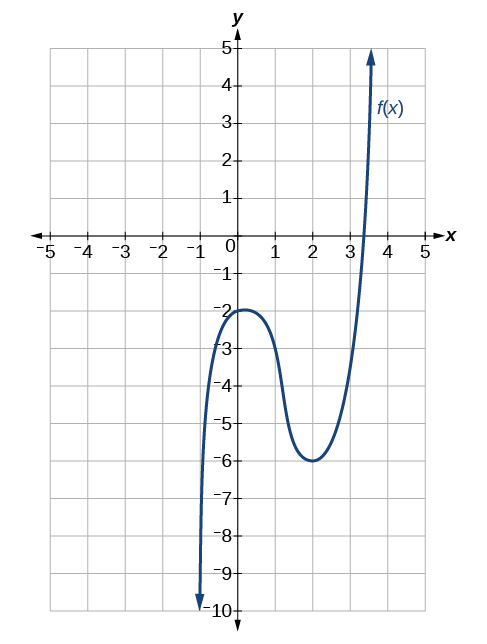
\(f(−1)\)
\(f(0)\)
\(f(0)=−2\)
\(f(1)\)
\(f(2)\)
\ (f (2) =−6f (2) =−6
\(f(3)\)
\(f′(−1)\)
\(f′(−1)=9\)
\(f′(0)\)
\(f′(1)\)
\(f′(1)=−3\)
\(f′(2)\)
\(f′(3)\)
\(f′(3)=9\)
Esboce a função com base nas informações abaixo:
\(f′(x)=2x, f(2)=4\)
Tecnologia
Avalie numericamente a derivada. Explore o comportamento do gráfico de\(f(x)=x^2\) around\(x=1\) representando graficamente a função nos seguintes domínios:\([ 0.9,1.1 ], [ 0.99,1.01 ], [ 0.999,1.001 ],\)\([0.9999, 1.0001]\) e. Podemos usar o recurso em nossa calculadora que define automaticamente Ymin e Ymax para os valores Xmin e Xmax que predefinimos. (Em algumas das calculadoras gráficas mais usadas, esse recurso pode ser chamado de ZOOM FIT ou ZOOM AUTO). Ao examinar os valores do intervalo correspondente para esta janela de visualização, aproxime como a curva muda, ou\(x=1,\) seja, aproxime a derivada em\(x=1.\)
As respostas variam. A inclinação da reta tangente próxima\(x=1\) é 2.
Aplicativos do mundo real
Para os exercícios a seguir, explique a notação em palavras. O volume\(f(t)\) de um tanque de gasolina, em galões,\(t\) minutos depois do meio dia.
\(f(0)=600\)
\(f'(30)=−20\)
Às 12h30, a taxa de variação do número de galões no tanque é de —20 galões por minuto. Ou seja, o tanque está perdendo 20 galões por minuto.
\(f(30)=0\)
\(f'(200)=30\)
200 minutos após o meio-dia, o volume de galões no tanque está mudando à taxa de 30 galões por minuto.
\(f(240)=500\)
Para os exercícios a seguir, explique as funções em palavras. A altura,\(s\), de um projétil após\(t\) segundos é dada por\(s(t)=−16t^2+80t.\)
\(s(2)=96\)
A altura do projétil após 2 segundos é de 96 pés.
\(s'(2)=16\)
\(s(3)=96\)
A altura do projétil em\(t=3\) segundos é de 96 pés.
\(s'(3)=−16\)
\(s(0)=0,s(5)=0.\)
A altura do projétil é zero\(t=0\) e novamente em\(t=5\). Em outras palavras, o projétil começa no chão e cai na Terra novamente após 5 segundos.
Para os exercícios a seguir, o volume\(V\) de uma esfera em relação ao seu raio\(r\) é dado por\(V=\frac{4}{3}πr^3.\)
Encontre a taxa média de variação da\(V\) medida que\(r\) muda de 1 cm para 2 cm.
Determine a taxa de variação instantânea de\(V\) quando r = 3 cm. r = 3 cm.
\(36π\)
Para os exercícios a seguir, a receita gerada pela venda de\(x\) itens é fornecida por\(R(x)=2x^2+10x\).
Encontre a variação média da função de receita conforme\(x\) as mudanças de\(x=10\) para\(x=20\).
Encontre\(R'(10)\) e interprete.
$50,00 por unidade, que é a taxa instantânea de variação da receita quando exatamente 10 unidades são vendidas.
Encontre\(R'(15)\) e interprete. Compare\(R'(15)\)\(R'(10),\) e explique a diferença.
Para os exercícios a seguir, o custo de produção de\(x\) celulares é descrito pela função\(C(x)=x^2−4x+1000.\)
Encontre a taxa média de variação no custo total à medida que\(x\) muda de\(x=10\) para\(x=15.\)
$21 por unidade
Encontre o custo marginal aproximado, quando 15 celulares tiverem sido produzidos, de produzir o 16º celular.
Encontre o custo marginal aproximado, quando 20 celulares tiverem sido produzidos, de produzir o 21º celular.
$36
Extensão
Para os exercícios a seguir, use a definição da derivada em um ponto\(x=a\),\(\lim \limits_{x \to a}\frac{f(x)−f(a)}{x−a},\) para encontrar a derivada das funções.
\(f(x)=\frac{1}{x^2}\)
\(f(x)=5x^2−x+4\)
\(f'(x)=10a−1\)
\(f(x)=−x^2+4x+7\)
\(f(x)=\frac{−4}{3−x^2}\)
\(\frac{4}{(3−x)^2}\)
Exercícios de revisão de
Encontrando limites: uma abordagem numérica e gráfica
Para os exercícios a seguir, use a Figura.
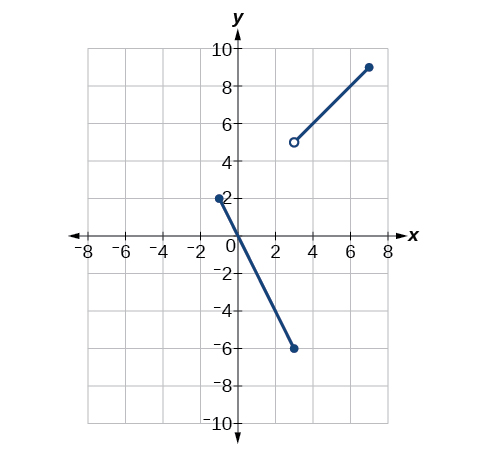
\(\lim \limits_{x \to −1^+}f(x)\)
2
\(\lim \limits_{x \to −1^−}f(x)\)
\(\lim \limits_{x \to −1} f(x)\)
não existe
\(\lim \limits_{x \to 3}f(x)\)
Em quais valores de a função\(x\) é descontínua? Qual condição de continuidade é violada?
Descontínuo em\(x=−1\) (\(\lim \limits_{x \to a} f(x)\)não existe),\(x=3\) (pule a descontinuidade) e\(x=7\) ((\ lim\ limits_ {x\ to a} f (x)\) não existe).
Usando a tabela, estime\(\lim \limits_{x \to 0}f(x).\)
| \(x\) | \(F(x)\) |
| −0,1 | 2.875 |
| −0,01 | 2,92 |
| −0,001 | 2.998 |
| 0 | Indefinido |
| 0,001 | 2.9987 |
| 0,01 | 2.865 |
| 0.1 | 2,78 145 |
| 0,15 | 2.678 |
3
Para os exercícios a seguir, com o uso de um utilitário gráfico, use evidências numéricas ou gráficas para determinar os limites esquerdo e direito da função dada como\(x\) abordagens\(a\). Se a função tiver limite à medida que\(x\) se aproxima\(a\), indique-o. Caso contrário, discuta por que não há limite.
\(f(x)=\begin{cases} | x |−1, && \text{if }x≠1 \\ x^3, \text{if }x=1 \end{cases} a=1\)
\(f(x)=\begin{cases} \frac{1}{x+1}, && \text{if }x=−2 \\ (x+1)^2, && \text{if }x≠−2 \end{cases} a=−2\)
\(\lim \limits_{x \to −2} f(x)=1\)
\(f(x)= \begin{cases} \sqrt{x+3} && \text{if } x < 1 \\ −\sqrt[3]{x} && \text{if }x>1 \end{cases} a=1\)
Encontrando limites: propriedades dos limites
Para os exercícios a seguir, encontre os limites se\(\lim \limits_{x \to c} f(x)=−3\)\(\lim \limits_{x \to c} g(x)=5\) e.
\(\lim \limits_{x \to c} (f(x)+g(x))\)
2
\(\lim \limits_{x \to c} \frac{f(x)}{g(x)}\)
\(\lim \limits_{x to c}(f(x)⋅g(x))\)
\(−15\)
\(\lim \limits_{x \to 0^+}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
\(\lim \limits_{x \to 0^-}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
3
\(\lim \limits_{x \to 3^+}(3x−〚x〛)\)
Para os exercícios a seguir, avalie os limites usando técnicas algébricas.
\(\lim \limits_{h \to 0}(\frac{(h+6)^2−36}{h})\)
12
\(\lim \limits_{x \to 25}(\frac{x^2−625}{\sqrt{x}−5)}\)
\(\lim \limits_{x \to 1}(\frac{−x^2−9x}{x})\)
−10
\(\lim \limits_{x \to 4}\frac{7−\sqrt{12x+1}}{x−4}\)
\(\lim \limits_{x \to −3}(\frac{\frac{1}{3}+\frac{1}{x}}{3+x})\)
\(−\frac{1}{9}\)
Continuidade
Para os exercícios a seguir, use evidências numéricas para determinar se o limite existe em\(x=a\). Caso contrário, descreva o comportamento do gráfico da função em\(x=a\).
\(f(x)=\frac{−2}{x−4}; a=4\)
\(f(x)=\frac{−2}{(x−4)^2}; a=4\)
Em\(x=4\), a função tem uma assíntota vertical.
\(f(x)=\frac{−x}{x^2−x−6}; a=3\)
\(f(x)=\frac{6x^2+23x+20}{4x^2−25}; a=−\frac{5}{2}\)
descontinuidade removível em\(a=−\frac{5}{2}\)
\(f(x)=\frac{\sqrt{x}−3}{9−x}; a=9\)
Para os exercícios a seguir, determine onde a função dada\(f(x)\) é contínua. Onde não é contínuo, indique quais condições falham e classifique quaisquer descontinuidades.
\(f(x)=x^2−2x−15\)
contínuo ligado\((−∞,∞)\)
\(f(x)=\frac{x^2−2x−15}{x−5}\)
\(f(x)=\frac{x^2−2x}{x^2−4x+4}\)
a descontinuidade removível em não\(x=2. f(2)\) está definida, mas existem limites.
\(f(x)=\frac{x^3−125}{2x^2−12x+10}\)
\(f(x)=\frac{x^2−\frac{1}{x}}{2−x}\)
descontinuidade em\(x=0\)\(x=2\) e. Ambos\(f(0)\) e não\(f(2)\) estão definidos.
\(f(x)=\frac{x+2}{x^2−3x−10}\)
\(f(x)=\frac{x+2}{x^3+8}\)
a descontinuidade removível em não\(x=–2. f(–2)\) está definida.
Derivados
Para os exercícios a seguir, encontre a taxa média de variação\(\frac{f(x+h)−f(x)}{h}\).
\(f(x)=3x+2\)
\(f(x)=5\)
0
\(f(x)=\frac{1}{x+1}\)
\(f(x)= \ln (x)\)
\(\frac{\ln (x+h)− \ln (x)}{h}\)
\(f(x)=e^{2x}\)
Para os exercícios a seguir, encontre a derivada da função.
\(f(x)=4x−6\)
\(=4\)
\(f(x)=5x^2−3x\)
Encontre a equação da reta tangente ao gráfico de\(f(x)\) no\(x\) valor indicado.
\(f(x)=−x^3+4x; x=2.\)
\(y=−8x+16\)
Para os exercícios a seguir, com a ajuda de um utilitário gráfico, explique por que a função não é diferenciável em todos os lugares em seu domínio. Especifique os pontos em que a função não é diferenciável.
\(f(x)=\frac{x}{| x |}\)
Dado que o volume de um cone circular reto é\(V=\frac{1}{3}πr^2h\) e que um determinado cone tem uma altura fixa de 9 cm e comprimento de raio variável, determine a taxa instantânea de mudança de volume em relação ao comprimento do raio quando o raio é de 2 cm. Dê uma resposta exata em termos de\(π\)
\(12π\)
Teste prático
Para os exercícios a seguir, use o gráfico de\(f\) na Figura.
\(f(1)\)
3
\(\lim \limits_{x \to −1^+}f(x)\)
\(\lim \limits_{x \to −1^-}f(x)\)
0
\(\lim \limits_{x \to −1}f(x)\)
\(\lim \limits_{x \to −2}f(x)\)
\(−1\)
Em quais valores de\(x\) é\(f\) descontínuo? Qual propriedade de continuidade é violada?
Para os exercícios a seguir, com o uso de um utilitário gráfico, use evidências numéricas ou gráficas para determinar os limites esquerdo e direito da função dada como\(x\) abordagens\(a\). Se a função tiver um limite à medida que\(x\) se aproxima\(a\), indique-o. Caso contrário, discuta por que não há limite
\(f(x)=\begin{cases} \frac{1}{x}−3, && \text{if }x≤2 \\ x^3+1, && \text{if } x>2 \end{cases} a=2\)
\(\lim \limits_{x \to 2^−} f(x)=−\frac{5}{2}a\)e,\(\lim \limits_{x \to 2^+} f(x)=9\) portanto, o limite da função quando\(x\) se aproxima de 2 não existe.
\(f(x)=\begin{cases} x^3+1, && \text{if }x<1 \\ 3x^2−1, && \text{if } x=1 \\ −\sqrt{x+3}+4, && \text{if } x>1 \end{cases} a=1\)
Para os exercícios a seguir, avalie cada limite usando técnicas algébricas.
\(\lim \limits_{x \to −5}(\frac{\frac{1}{5}+\frac{1}{x}}{10+2x})\)
\(−\frac{1}{50}\)
\(\lim \limits_{h \to 0} (\frac{\sqrt{h^2+25}−5}{h^2})\)
\(\lim \limits_{h \to 0} (\frac{1}{h}−\frac{1}{h^2+h})\)
1
Para os exercícios a seguir, determine se a função dada\(f\) é contínua ou não. Se for contínuo, mostre o porquê. Se não for contínuo, indique quais condições falham.
\(f(x)=\sqrt{x^2−4}\)
\(f(x)=\frac{x^3−4x^2−9x+36}{x^3−3x^2+2x−6}\)
descontinuidade removível em\(x=3\)
Para os exercícios a seguir, use a definição de uma derivada para encontrar a derivada da função dada em\(x=a\).
\(f(x)=\frac{3}{5+2x}\)
\(f(x)=\frac{3}{\sqrt{x}}\)
\(f'(x)=−\frac{3}{2a^{\frac{3}{2}}}\)
\(f(x)=2x^2+9x\)
descontínuo em —2,0, não diferenciável em —2,0, 2.
Para os exercícios a seguir, com a ajuda de um utilitário gráfico, explique por que a função não é diferenciável em todos os lugares em seu domínio. Especifique os pontos em que a função não é diferenciável.
\(f(x)=| x−2 |−| x+2 |\)
\(f(x)=\frac{2}{1+e^{\frac{2}{x}}}\)
não diferenciável em\(x=0\) (sem limite)
Para os exercícios a seguir, explique a notação em palavras quando a altura de um projétil em pés\(s\),, é uma função do tempo t t em segundos após o lançamento e é dada pela função\(s(t)\).
\(s(0)\)
\(s(2)\)
a altura do projétil em\(t=2\) segundos
\(s'(2)\)
\(\frac{s(2)−s(1)}{2−1}\)
a velocidade média de\(t=1\) até\(t=2\)
\(s(t)=0\)
Para os exercícios a seguir, use a tecnologia para avaliar o limite.
\(\lim \limits_{x \to 0} \frac{\sin (x)}{3x}\)
\(\frac{1}{3}\)
\(\lim \limits_{x \to 0} \frac{\tan ^2 (x)}{2x}\)
\(\lim \limits_{x \to 0}\frac{\sin (x)(1−\cos (x))}{2x^2}\)
0
Avalie o limite manualmente.
\(\lim \limits_{x \to 1}f(x), \text{where } f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Em que valor (es) de a função abaixo\(x\) é descontínua?
\(f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Para os exercícios a seguir, considere a função cujo gráfico aparece na Figura.
Encontre a taxa média de variação da função de\(x=1\) para\(x=3\).
2
Encontre todos os valores de\(x\) at which\(f'(x)=0\).
\(x=1\)
Encontre todos os valores de\(x\) at que\(f'(x)\) não existam.
Encontre uma equação da reta tangente ao gráfico\(f\) do ponto indicado:\(f(x)=3x^2−2x−6, x=−2\)
\(y=−14x−18\)
Para os exercícios a seguir, use a função\(f(x)=x(1−x)^{\frac{2}{5}}\).
Faça um gráfico da função\(f(x)=x(1−x)^{\frac{2}{5}}\) inserindo\(f(x)=x((1−x)^2)^{\frac{1}{5}}\) e depois inserindo\(f(x)=x((1−x)^{\frac{1}{5}})^2\).
Explore o comportamento do gráfico de\(f(x)\) cerca\(x=1\) representando graficamente a função nos seguintes domínios, [0,9, 1,1], [0,99, 1,01], [0,999, 1,001] e [0,9999, 1,0001]. Use essas informações para determinar se a função parece ser diferenciável em\(x=1\).
O gráfico não é diferenciável em\(x=1\) (cúspide).
Para os exercícios a seguir, encontre a derivada de cada uma das funções usando a definição:\(\lim \limits_{h \to 0} \frac{f(x+h)−f(x)}{h}\)
\(f(x)=2x−8\)
\(f(x)=4x^2−7\)
\(f′(x)=8x\)
\(f(x)=x−\frac{1}{2}x^2\)
\(f(x)=\frac{1}{x+2}\)
\(f'(x)=−\frac{1}{(2+x)^2}\)
\(f(x)=\frac{3}{x−1}\)
\(f(x)=−x^3+1\)
\(f′(x)=−3^x2\)
\(f(x)=x^2+x^3\)
\(f(x)=\sqrt{x−1}\)
\(f'(x)=\frac{1}{2\sqrt{x−1}}\)
Notas de pé
- 1 www.csun.edu/science/health/d... tv&health.html Fonte fornecida.
Glossário
- taxa média de variação
- a inclinação da linha que liga os dois pontos\((a,f(a))\) e\((a+h,f(a+h))\) na curva de\(f(x)\); é dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}.\]
- derivado
- a inclinação de uma função em um determinado ponto; denotada\(f′(a)\), em um ponto em\(x=a\) que está\(f′(a)=\lim \limits_{h \to 0}\frac{f(a+h)−f(a)}{h}\), desde que o limite exista.
- diferenciável
- uma função\(f(x)\) para a qual a derivada existe em\(x=a.\) Em outras palavras, se f′( a) f′f (a) existir.
- taxa instantânea de mudança
- a inclinação de uma função em um determinado ponto;\(x=a\) nela é dada por\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
- velocidade instantânea
- a mudança na velocidade ou direção em um determinado instante; uma função\(s(t)\) representa a posição de um objeto no tempo\(t\), e a velocidade ou velocidade instantânea do objeto no momento\(t=a\) é dada por\(s′(a)=\lim \limits_{h \to 0}\frac{s(a+h)−s(a)}{h}\).
- linha secante
- uma linha que cruza dois pontos em uma curva
- linha tangente
- uma linha que cruza uma curva em um único ponto


