11.7: Probabilidade
- Page ID
- 189190
- Construa modelos de probabilidade.
- Calcule probabilidades de resultados igualmente prováveis.
- Calcule as probabilidades da união de dois eventos.
- Use a regra do complemento para encontrar probabilidades.
- Calcule a probabilidade usando a teoria da contagem.
Os residentes do sudeste dos Estados Unidos estão muito familiarizados com os gráficos, conhecidos como modelos de espaguete, como o da Figura\(\PageIndex{1}\). Eles combinam uma coleção de dados meteorológicos para prever a trajetória mais provável de um furacão. Cada linha colorida representa um caminho possível. O grupo de linhas onduladas pode começar a se assemelhar a fios de espaguete, daí o nome. Nesta seção, investigaremos métodos para fazer esses tipos de previsões.
Figura\(\PageIndex{1}\): Um exemplo de “modelo de espaguete”, que pode ser usado para prever possíveis caminhos de uma tempestade tropical. 1
Construindo modelos de probabilidade
Suponha que rolemos um cubo numérico de seis lados. Rolar um cubo numérico é um exemplo de experimento ou atividade com um resultado observável. Os números no cubo são resultados possíveis, ou resultados, desse experimento. O conjunto de todos os resultados possíveis de um experimento é chamado de espaço amostral do experimento. O espaço amostral para este experimento é\(\{1,2,3,4,5,6 \}\). Um evento é qualquer subconjunto de um espaço amostral.
A probabilidade de um evento é conhecida como probabilidade. A probabilidade de um evento pp é um número que sempre satisfaz\(0≤p≤1\), onde\(0\) indica um evento impossível e\(1\) indica um determinado evento. Um modelo de probabilidade é uma descrição matemática de um experimento listando todos os resultados possíveis e suas probabilidades associadas. Por exemplo, se houver uma\(1\%\) chance de ganhar um sorteio e uma\(99\%\) chance de perder o sorteio, um modelo de probabilidade seria muito parecido com a Tabela\(\PageIndex{1}\).
| Resultado | Probabilidade |
|---|---|
| Ganhando o sorteio | 1% |
| Perder o sorteio | 99% |
A soma das probabilidades listadas em um modelo de probabilidade deve ser igual a\(1\), ou\(100\%\).
- Identifique cada resultado.
- Determine o número total de resultados possíveis.
- Compare cada resultado com o número total de resultados possíveis.
Construa um modelo de probabilidade para rolar um dado único e justo, com o evento sendo o número mostrado no dado.
Solução
Comece fazendo uma lista de todos os resultados possíveis para o experimento. Os resultados possíveis são os números que podem ser acumulados:\(1\)\(2\)\(3\),\(4\),\(5\),,\(6\) e. Há seis resultados possíveis que compõem o espaço amostral.
Atribua probabilidades a cada resultado no espaço amostral determinando uma razão entre o resultado e o número de resultados possíveis. Há um de cada um dos seis números no cubo, e não há razão para pensar que alguma face em particular tenha mais probabilidade de aparecer do que qualquer outra, então a probabilidade de rolar qualquer número é\(16\).
| Resultado | Rolo de 1 | Rolo de 2 | Rolo de 3 | Rolo de 4 | Rolo de 5 | Rolo de 6 |
|---|---|---|---|---|---|---|
| Probabilidade | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Não. As probabilidades podem ser expressas como frações, decimais ou porcentagens. A probabilidade deve ser sempre um número entre\(0\) e\(1\), inclusive de\(0\)\(1\) e.
Calculando probabilidades de resultados igualmente prováveis
\(S\)Seja um espaço de amostra para um experimento. Ao investigar a probabilidade, um evento é qualquer subconjunto de\(S\). Quando os resultados de um experimento são todos igualmente prováveis, podemos encontrar a probabilidade de um evento dividindo o número de resultados no evento pelo número total de resultados em\(S\). Suponha que um cubo numérico seja lançado e estejamos interessados em encontrar a probabilidade do evento “rolar um número menor ou igual a 4”. Existem 4 resultados possíveis no evento e 6 resultados possíveis em\(S\), então a probabilidade do evento é\(\dfrac{4}{6}=\dfrac{2}{3}\).
A probabilidade de um evento\(E\) em um experimento com espaço amostral\(S\) com resultados igualmente prováveis é dada por
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\)é um subconjunto de\(S\), então é sempre verdade que\(0≤P(E)≤1\).
Um cubo numérico é rolado. Encontre a probabilidade de rolar um número ímpar.
Solução
O evento “rolando um número ímpar” contém três resultados. Há resultados\(6\) igualmente prováveis no espaço amostral. Divida para encontrar a probabilidade do evento.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Um cubo numérico é rolado. Encontre a probabilidade de rolar um número maior que\(2\).
- Resposta
-
\(\dfrac{2}{3}\)
Calculando a probabilidade da união de dois eventos
Muitas vezes estamos interessados em descobrir a probabilidade de que um dos vários eventos ocorra. Suponha que estejamos jogando um jogo de cartas e ganharemos se a próxima carta sorteada for um coração ou um rei. Estaríamos interessados em descobrir a probabilidade da próxima carta ser um coração ou um rei. A união de dois eventos\(E\) e\(F\), escrito\(E\cup F\), é o evento que ocorre se um ou ambos os eventos ocorrerem.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Suponha que o spinner na Figura\(\PageIndex{2}\) esteja girado. Queremos encontrar a probabilidade de girar laranja ou girar uma\(b\).
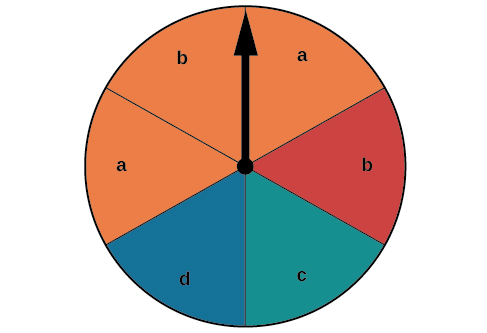
Figura\(\PageIndex{2}\): Um gráfico circular com seis opções.
Há um total de\(6\) seções, e\(3\) delas são laranja. Portanto, a probabilidade de girar laranja é\(\dfrac{3}{6}=\dfrac{1}{2}\). Há um total de\(6\) seções, e\(2\) delas têm uma\(b\). Portanto, a probabilidade de girar a\(b\) é\(\dfrac{2}{6}=\dfrac{1}{3}\). Se somarmos essas duas probabilidades, estaríamos contando o setor que é laranja e\(b\) duas vezes. Para encontrar a probabilidade de girar uma laranja ou uma\(b\), precisamos subtrair a probabilidade de que o setor seja laranja e tenha um\(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
A probabilidade de girar laranja ou a\(b\) é\(\dfrac{2}{3}\).
A probabilidade da união de dois eventos\(E\) e\(F\) (escrito\(E\cup F\)) é igual à soma da probabilidade de\(E\) e da probabilidade de\(F\) menos a probabilidade de\(E\)\(F\) ocorrer juntos (o que é chamado de interseção de\(E\) \(F\)e é escrito como\(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Uma carta é retirada de um baralho padrão. Encontre a probabilidade de desenhar um coração ou um\(7\).
Solução
Um baralho padrão contém um número igual de corações, diamantes, paus e espadas. Portanto, a probabilidade de desenhar um coração é\(\dfrac{1}{4}\). Há quatro\(7s\) em um baralho padrão e um total de\(52\) cartas. Portanto, a probabilidade de desenhar um\(7\) é\(\dfrac{1}{13}\).
A única carta no baralho que é ao mesmo tempo um coração e um\(7\) é a\(7\) de copas, então a probabilidade de tirar um coração e um\(7\) é\(\dfrac{1}{52}\). Substitua\(P(H)=\dfrac{1}{4}\)\(P(7)=\dfrac{1}{13}\), e\(P(H\cap 7)=\dfrac{1}{52}\) na fórmula.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
A probabilidade de desenhar um coração ou um\(7\) é\(\dfrac{4}{13}\).
Uma carta é retirada de um baralho padrão. Encontre a probabilidade de tirar um cartão vermelho ou um ás.
- Resposta
-
\(\dfrac{7}{13}\)
Calculando a probabilidade de eventos mutuamente exclusivos
Suponha que o spinner na Figura\(\PageIndex{2}\) seja girado novamente, mas desta vez estamos interessados na probabilidade de girar uma laranja ou uma\(d\). Não há setores que sejam alaranjados e contenham um\(d\), então esses dois eventos não têm resultados em comum. Diz-se que os eventos são eventos mutuamente exclusivos quando não têm resultados em comum. Como não há sobreposição, não há nada para subtrair, então a fórmula geral é
\[P(E\cap F)=P(E)+P(F)\]
Observe que, com eventos mutuamente exclusivos, a interseção de\(E\) e\(F\) é o conjunto vazio. A probabilidade de girar uma laranja é\(\dfrac{3}{6}=\dfrac{1}{2}\) e a probabilidade de girar um\(d\) é\(\dfrac{1}{6}\). Podemos encontrar a probabilidade de girar uma laranja ou\(d\) simplesmente somando as duas probabilidades.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
A probabilidade de girar uma laranja ou um\(d\) é\(\dfrac{2}{3}\).
A probabilidade da união de dois eventos mutuamente exclusivos\(E\) e\(F\) é dada por
\[P(E\cap F)=P(E)+P(F)\]
- Determine o número total de resultados do primeiro evento.
- Encontre a probabilidade do primeiro evento.
- Determine o número total de resultados para o segundo evento.
- Encontre a probabilidade do segundo evento.
- Adicione as probabilidades.
Uma carta é retirada de um baralho padrão. Encontre a probabilidade de desenhar um coração ou uma pá.
Solução
Os eventos “desenhar um coração” e “desenhar uma pá” são mutuamente exclusivos porque não podem ocorrer ao mesmo tempo. A probabilidade de desenhar um coração é\(\dfrac{1}{4}\), e a probabilidade de desenhar uma pá também\(\dfrac{1}{4}\), então a probabilidade de desenhar um coração ou uma pá é
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
Uma carta é retirada de um baralho padrão. Encontre a probabilidade de desenhar um ás ou um rei.
- Resposta
-
\(\dfrac{2}{13}\)
Usando a regra do complemento para calcular probabilidades
Discutimos como calcular a probabilidade de um evento acontecer. Às vezes, estamos interessados em descobrir a probabilidade de um evento não acontecer. O complemento de um evento\(E\), denotado\(E′\), é o conjunto de resultados no espaço amostral que não estão em\(E\). Por exemplo, suponha que estejamos interessados na probabilidade de um cavalo perder uma corrida. Se o evento\(W\) é o cavalo vencendo a corrida, então o complemento do evento\(W\) é o cavalo perdendo a corrida.
Para encontrar a probabilidade de o cavalo perder a corrida, precisamos usar o fato de que a soma de todas as probabilidades em um modelo de probabilidade deve ser\(1\).
\[P(E′)=1−P(E)\]
A probabilidade de o cavalo ganhar somada à probabilidade de o cavalo perder deve ser igual\(1\) a. Portanto, se a probabilidade de o cavalo ganhar a corrida é\(\dfrac{1}{9}\), a probabilidade de o cavalo perder a corrida é simplesmente
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
A probabilidade de que o complemento de um evento ocorra é dada por
\[P(E′)=1−P(E)\]
Dois cubos numéricos de seis lados são enrolados.
- Determine a probabilidade de que a soma dos números obtidos seja menor ou igual\(3\) a.
- Encontre a probabilidade de que a soma dos números obtidos seja maior que\(3\).
Solução
O primeiro passo é identificar o espaço amostral, que consiste em todos os resultados possíveis. Existem dois cubos numéricos e cada cubo numérico tem seis resultados possíveis. Usando o Princípio de Multiplicação, descobrimos que existem\(6×6\) ou\(36\) totalizam resultados possíveis. Então, por exemplo,\(1-1\) representa um\(1\) rolo em cada cubo numérico.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- Precisamos contar o número de maneiras de obter uma soma igual\(3\) ou inferior. Isso incluiria os seguintes resultados:\(1-1\)\(1-2\),,\(2-1\) e. Portanto, existem apenas três maneiras de obter uma soma igual\(3\) ou inferior. A probabilidade é
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- Em vez de listar todas as possibilidades, podemos usar a Regra do Complemento. Como já encontramos a probabilidade do complemento desse evento, podemos simplesmente subtrair essa probabilidade de\(1\) para encontrar a probabilidade de que a soma dos números obtidos seja maior que\(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Dois cubos numéricos são lançados. Use a Regra do Complemento para encontrar a probabilidade de que a soma seja menor que\(10\).
- Resposta
-
\(\dfrac{5}{6}\)
Computando probabilidade usando a teoria da contagem
Muitos problemas de probabilidade interessantes envolvem a contagem de princípios, permutações e combinações. Nesses problemas, usaremos permutações e combinações para encontrar o número de elementos em eventos e espaços de amostra. Esses problemas podem ser complicados, mas podem ser facilitados dividindo-os em problemas de contagem menores.
Suponha, por exemplo, que uma loja tenha telefones\(8\) celulares e que\(3\) esses estejam com defeito. Talvez queiramos descobrir a probabilidade de um casal que compra\(2\) telefones receber\(2\) telefones que não estão com defeito. Para resolver esse problema, precisamos calcular todas as formas de selecionar\(2\) telefones que não estão com defeito, bem como todas as formas de selecionar\(2\) telefones. Existem\(5\) telefones que não estão com defeito, então existem\(C(5,2)\) maneiras de selecionar\(2\) telefones que não estão com defeito. Existem\(8\) telefones, então existem\(C(8,2)\) maneiras de selecionar\(2\) telefones. A probabilidade de selecionar\(2\) telefones que não estejam com defeito é:
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Uma criança seleciona aleatoriamente\(5\) brinquedos de uma lixeira contendo\(3\) coelhos,\(5\) cachorros e\(6\) ursos.
- Encontre a probabilidade de que apenas ursos sejam escolhidos.
- Descubra a probabilidade de que\(2\) ursos e\(3\) cães sejam escolhidos.
- Encontre a probabilidade de que pelo menos\(2\) cães sejam escolhidos.
Solução
- Precisamos contar o número de maneiras de escolher apenas ursos e o número total de maneiras possíveis de selecionar\(5\) brinquedos. Existem\(6\) ursos, então existem\(C(6,5)\) maneiras de escolher\(5\) ursos. Existem\(14\) brinquedos, então existem\(C(14,5)\) maneiras de escolher qualquer\(5\) brinquedo.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- Precisamos contar o número de maneiras de escolher\(2\) ursos e\(3\) cães e o número total de maneiras possíveis de selecionar\(5\) brinquedos. Existem\(6\) ursos, então existem\(C(6,2)\) maneiras de escolher\(2\) ursos. Existem\(5\) cachorros, então existem\(C(5,3)\) maneiras de escolher\(3\) cães. Como estamos escolhendo ursos e cães ao mesmo tempo, usaremos o Princípio de Multiplicação. Existem\(C(6,2)⋅C(5,3)\) maneiras de escolher\(2\) ursos e\(3\) cachorros. Podemos usar esse resultado para encontrar a probabilidade.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- Geralmente, é mais fácil resolver “pelo menos” problemas usando a Regra do Complemento. Começaremos descobrindo a probabilidade de que menos\(2\) cães sejam escolhidos. Se menos de\(2\) cães forem escolhidos, nenhum cachorro poderá ser escolhido ou\(1\) um cachorro poderá ser escolhido.
Quando nenhum cachorro é escolhido, todos os\(5\) brinquedos vêm de\(9\) brinquedos que não são cães. Existem\(C(9,5)\) maneiras de escolher\(9\) brinquedos que não sejam cachorros. Como existem\(14\) brinquedos, existem\(C(14,5)\) maneiras de escolher os\(5\) brinquedos de todos os brinquedos.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
Se o\(1\) cão for escolhido, os\(4\) brinquedos devem vir dos\(9\) brinquedos que não são cães e\(1\) devem vir dos\(5\) cães. Como estamos escolhendo cães e outros brinquedos ao mesmo tempo, usaremos o Princípio de Multiplicação. Existem\(C(5,1)⋅C(9,4)\) maneiras de escolher\(1\) cães e\(1\) outros brinquedos.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Como esses eventos não ocorreriam juntos e, portanto, são mutuamente exclusivos, adicionamos as probabilidades para encontrar a probabilidade de que menos\(2\) cães sejam escolhidos.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
Em seguida, subtraímos essa probabilidade de\(1\) para encontrar a probabilidade de que pelo menos\(2\) cães sejam escolhidos.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
Uma criança seleciona aleatoriamente\(3\) gumballs de um recipiente com chicletes\(4\) roxos,\(8\) amarelos e\(2\) verdes.
- Determine a probabilidade de que todos os\(3\) chicletes selecionados sejam roxos.
- Encontre a probabilidade de que nenhum chiclete amarelo seja selecionado.
- Encontre a probabilidade de que pelo menos um chiclete\(1\) amarelo seja selecionado.
- Resposta
-
\(\dfrac{1}{91}\)
- Resposta
-
\(\dfrac{5}{91}\)
- Resposta
-
\(\dfrac{86}{91}\)
Acesse esses recursos on-line para obter instruções adicionais e praticar com probabilidade.
Visite este site para obter mais perguntas práticas do Learningpod.
Equações-chave
| probabilidade de um evento com resultados igualmente prováveis | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| probabilidade da união de dois eventos | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| probabilidade da união de eventos mutuamente exclusivos | \(P(E\cup F)=P(E)+P(F)\) |
| probabilidade do complemento de um evento | \(P(E')=1−P(E)\) |
Conceitos-chave
- Probabilidade é sempre um número entre\(0\) e\(1\), onde\(0\) significa que um evento é impossível e\(1\) significa que um evento é certo.
- As probabilidades em um modelo de probabilidade devem somar\(1\) a. Veja o exemplo\(\PageIndex{1}\).
- Quando os resultados de um experimento são todos igualmente prováveis, podemos encontrar a probabilidade de um evento dividindo o número de resultados no evento pelo número total de resultados no espaço amostral do experimento. Veja o exemplo\(\PageIndex{2}\).
- Para encontrar a probabilidade da união de dois eventos, adicionamos as probabilidades dos dois eventos e subtraímos a probabilidade de que ambos os eventos ocorram simultaneamente. Veja o exemplo\(\PageIndex{3}\).
- Para encontrar a probabilidade da união de dois eventos mutuamente exclusivos, adicionamos as probabilidades de cada um dos eventos. Veja o exemplo\(\PageIndex{4}\).
- A probabilidade do complemento de um evento é a diferença entre\(1\) e a probabilidade de que o evento ocorra. Veja o exemplo\(\PageIndex{5}\).
- Em alguns problemas de probabilidade, precisamos usar permutações e combinações para encontrar o número de elementos em eventos e espaços de amostra. Veja o exemplo\(\PageIndex{6}\).


