11.1: Sequências e suas notações
- Page ID
- 189191
- Escreva os termos de uma sequência definida por uma fórmula explícita.
- Escreva os termos de uma sequência definida por uma fórmula recursiva.
- Use notação fatorial.
Uma empresa de videogames lança uma nova e empolgante campanha publicitária. Eles preveem que o número de visitas on-line ao seu site, ou visitas, dobrará a cada dia. O modelo que eles estão usando mostra\(2\) o primeiro dia,\(4\) chega ao segundo dia,\(8\) chega ao terceiro dia e assim por diante (Tabela\(\PageIndex{1}\)).
| Dia | 1 | 2 | 3 | 4 | 5 | ... |
|---|---|---|---|---|---|---|
| Sucessos | 2 | 4 | 8 | 16 | 32 | ... |
Se o modelo deles continuar, quantos acessos haverá no final do mês? Para responder a essa pergunta, primeiro precisamos saber como determinar uma lista de números escritos em uma ordem específica. Nesta seção, exploraremos esses tipos de listas ordenadas.
Escrevendo os termos de uma sequência definida por uma fórmula explícita
Uma forma de descrever uma lista ordenada de números é como uma sequência. Uma sequência é uma função cujo domínio é um subconjunto dos números de contagem. A sequência estabelecida pelo número de acessos no site é
\(\{ 2,4,8,16,32,…\}\)
As reticências (...) indicam que a sequência continua indefinidamente. Cada número na sequência é chamado de termo. Os primeiros cinco termos dessa sequência são\(2\)\(4\),\(8\)\(16\),,\(32\) e.
Listar todos os termos de uma sequência pode ser complicado. Por exemplo, encontrar o número de acessos no site no final do mês exigiria a listagem de tantos\(31\) termos quanto os termos. Uma forma mais eficiente de determinar um termo específico é escrever uma fórmula para definir a sequência.
Um tipo de fórmula é uma fórmula explícita, que define os termos de uma sequência usando sua posição na sequência. Fórmulas explícitas são úteis se quisermos encontrar um termo específico de uma sequência sem encontrar todos os termos anteriores. Podemos usar a fórmula para encontrar o enésimo termo da sequência, onde nn é qualquer número positivo. Em nosso exemplo, cada número na sequência é o dobro do número anterior, então podemos usar potências de 2 para escrever uma fórmula para o enésimo termo.

O primeiro termo da sequência é\(2^1=2\), o segundo termo é\(2^2=4\), o terceiro termo é\(2^3=8\) e assim por diante. O enésimo termo da sequência pode ser encontrado elevando 2 à enésima potência. Uma fórmula explícita para uma sequência é nomeada por uma letra minúscula\(a\)\(b\),,\(c\)... com o subscrito\(n\). A fórmula explícita para essa sequência é
\(a_n=2^n\)
Agora que temos uma fórmula para o enésimo termo da sequência, podemos responder à pergunta feita no início desta seção. Fomos convidados a encontrar o número de acessos no final do mês, que levaremos em 31 dias. Para encontrar o número de acessos no último dia do mês, precisamos encontrar o 31º termo da sequência. Substituiremos 31 por\(n\) na fórmula.
\[ \begin{align*} a_{31}=2^{31} \\ [5pt] &=2,147,483,648 \end{align*}\]
Se a tendência de duplicação continuar, a empresa\(2,147,483,648\) receberá resultados no último dia do mês. Isso é mais de um\(2.1\) bilhão de acessos! O grande número provavelmente é um pouco irreal porque não leva em conta o interesse do consumidor e a concorrência. No entanto, isso dá à empresa um ponto de partida para considerar as decisões de negócios.
Outra forma de representar a sequência é usando uma tabela. Os primeiros cinco termos da sequência e o enésimo termo da sequência são mostrados na Tabela\(\PageIndex{2}\).
| \(n\) | 1 | 2 | 3 | 4 | 5 | \(n\) |
|---|---|---|---|---|---|---|
| \(n^{th}\)termo da sequência,\(a_n\) | 2 | 4 | 8 | 16 | 32 | \(2^n\) |
A representação gráfica fornece uma representação visual da sequência como um conjunto de pontos distintos. Podemos ver no gráfico da Figura\(\PageIndex{1}\) que o número de acertos está aumentando a uma taxa exponencial. Essa sequência específica forma uma função exponencial.
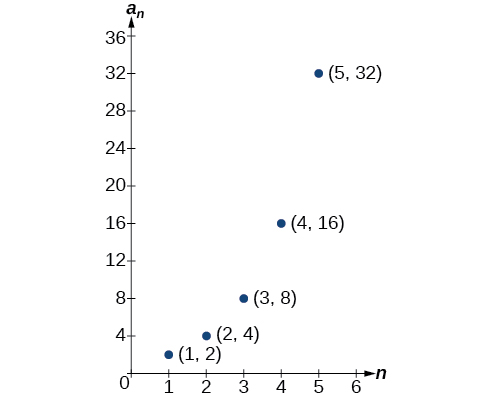
Figura\(\PageIndex{1}\)
Por fim, podemos escrever essa sequência específica como
\(\{2,4,8,16,32,…,2^n,…\}\)
Uma sequência que continua indefinidamente é chamada de sequência infinita. O domínio de uma sequência infinita é o conjunto de números contados. Se considerarmos apenas os primeiros\(10\) termos da sequência, poderíamos escrever
\(\{2,4,8,16,32,…,2^n,…,1024\}\)
Essa sequência é chamada de sequência finita porque não continua indefinidamente.
Uma sequência é uma função cujo domínio é o conjunto de números inteiros positivos. Uma sequência finita é uma sequência cujo domínio consiste somente nos primeiros números inteiros\(n\) positivos. Os números em uma sequência são chamados de termos. A variável\(a\) com um número subscrito é usada para representar os termos em uma sequência e para indicar a posição do termo na sequência.
\[a_1,a_2,a_3,…,a_n,…\]
Chamamos\(a_1\) o primeiro termo da sequência,\(a_2\) o segundo termo da sequência,\(a_3\) o terceiro termo da sequência e assim por diante. O termo\(a_n\) é chamado de enésimo termo da sequência ou termo geral da sequência. Uma fórmula explícita define o enésimo termo de uma sequência usando a posição do termo. Uma sequência que continua indefinidamente é uma sequência infinita.
Não. Em certos problemas, pode ser útil definir o termo inicial como\(a_0\) em vez de\(a_1\). Nesses problemas, o domínio da função inclui\(0\).
- Substitua cada valor de\(n\) na fórmula. Comece\(n=1\) para encontrar o primeiro termo,\(a_1\).
- Para encontrar o segundo termo\(a_2\), use\(n=2\).
- Continue da mesma maneira até identificar todos os termos nn.
Escreva os primeiros cinco termos da sequência definida pela fórmula explícita\(a_n=−3n+8\).
Solução
\(n=1\)Substitua na fórmula. Repita com valores\(2\) até\(5\) for\(n\).
\(\begin{array}{ll} n=1 & a_1=−3(1)+8=5 \\ n=2 & a_2=−3(2)+8=2 \\ n=3 & a_3=−3(3)+8=−1 \\ n=4 & a_4=−3(4)+8=−4 \\ n=5 & a_5=−3(5)+8=−7 \end{array}\)
Os primeiros cinco termos são\(\{5,2,−1,−4,−7\}\).
Análise
Os valores da sequência podem ser listados em uma tabela. Uma tabela, como Tabela\(\PageIndex{3}\), é uma forma conveniente de inserir a função em um utilitário gráfico.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(a_n\) | 5 | 2 | —1 | —4 | —7 |
Um gráfico pode ser feito a partir dessa tabela de valores. A partir do gráfico na Figura\(\PageIndex{2}\), podemos ver que essa sequência representa uma função linear, mas observe que o gráfico não é contínuo porque o domínio está apenas sobre os números inteiros positivos.

Figura\(\PageIndex{2}\)
Escreva os primeiros cinco termos da sequência definida pela fórmula explícita\(t_n=5n−4\).
- Resposta
-
Os primeiros cinco termos são\(\{1,6, 11, 16, 21\}\).
Investigando sequências alternadas
Às vezes, as sequências têm termos que são alternativos. Na verdade, os termos podem realmente se alternar em signos. As etapas para encontrar os termos da sequência são as mesmas como se os sinais não se alternassem. No entanto, os termos resultantes não mostrarão aumento ou diminuição como\(n\) aumentos. Vamos dar uma olhada na sequência a seguir.
\(\{2,−4,6,−8\}\)
Observe que o primeiro termo é maior que o segundo termo, o segundo termo é menor que o terceiro termo e o terceiro termo é maior que o quarto termo. Essa tendência continua para sempre. Não reorganize os termos em ordem numérica para interpretar a sequência.
- Substitua cada valor de nn na fórmula. Comece\(n=1\) para encontrar o primeiro termo,\(a_1\). O sinal do termo é dado pelo\({(−1)}^n\) na fórmula explícita.
- Para encontrar o segundo termo\(a_2\), use\(n=2\).
- Continue da mesma maneira até identificar todos os\(n\) termos.
Escreva os primeiros cinco termos da sequência.
\(a_n=\dfrac{{(−1)}^nn^2}{n+1}\)
Solução
Substitua\(n=1\)\(n=2\),, e assim por diante na fórmula.
\(\begin{array}{ll} n=1 & a_1=\dfrac{{(−1)}^12^2}{1+1}=−\dfrac{1}{2} \\ n=2 & a_2=\dfrac{{(−1)}^22^2}{2+1}=\dfrac{4}{3} \\ n=3 & a_3=\dfrac{{(−1)}^33^2}{3+1}=−\dfrac{9}{4} \\ n=4 & a_4=\dfrac{{(−1)}^44^2}{4+1}=\dfrac{16}{5} \\ n=5 & a_5=\dfrac{{(−1)}^55^2}{5+1}=−\dfrac{25}{6} \end{array}\)
Os primeiros cinco termos são\(\{−12,43,−94,165,−256\}\).
Análise
O gráfico dessa função, mostrado na Figura\(\PageIndex{3}\), parece diferente dos que vimos anteriormente nesta seção porque os termos da sequência alternam entre valores positivos e negativos.

Figura\(\PageIndex{3}\)
Sim, o poder pode ser\(n\),\(n+1\)\(n−1\), e assim por diante, mas qualquer poder estranho resultará em um termo negativo, e qualquer poder par resultará em um termo positivo.
Escreva os primeiros cinco termos da sequência:
\(a_n=\dfrac{4n}{{(−2)}^n}\)
- Resposta
-
Os primeiros cinco termos são\(\{−2, 2, −32, 1, −58\}\).
Investigando fórmulas explícitas por partes
Aprendemos que sequências são funções cujo domínio está acima dos números inteiros positivos. Isso vale para outros tipos de funções, incluindo algumas funções por partes. Lembre-se de que uma função por partes é uma função definida por várias subseções. Uma fórmula diferente pode representar cada subseção individual.
- Identifique a fórmula à qual\(n=1\) se aplica.
- Para encontrar o primeiro termo\(a_1\), use\(n=1\) na fórmula apropriada.
- Identifique a fórmula à qual\(n=2\) se aplica.
- Para encontrar o segundo termo\(a_2\), use\(n=2\) na fórmula apropriada.
- Continue da mesma maneira até identificar todos os\(n\) termos.
Escreva os primeiros seis termos da sequência.
\(a_n=\begin{cases}n^2\space \text{if n is not divisible by } 3\\\dfrac{n}{3} \text{if n is divisible by } 3\end{cases}\)
Solução
Substitua\(n=1\)\(n=2\),, e assim por diante na fórmula apropriada. Use\(n^2\) quando não\(n\) for múltiplo de\(3\). Use\(n^3\) quando\(n\) for múltiplo de\(3\).
\(\begin{array}{ll} a_1=1^2=1 & 1 \text{ is not a multiple of }3. \text{ Use } n^2. \\ a_2=2^2=4 & 2 \text{ is not a multiple of }3 \text{ . Use }n^2. \\ a_3=\dfrac{3}{3}=1 & 3 \text{ is a multiple of }3 \text{. Use }\dfrac{n}{3}. \\ a_4=4^2=16 & 4 \text{ is not a multiple of }3. \text{ Use }n^2. \\ a_5=5^2=25 & 5 \text{ is not a multiple of } 3. \text{Use }n^2. \\ a_6=\dfrac{6}{3}=2 & 6 \text{ is a multiple of }3. \text{Use }\dfrac{n}{3} \end{array}\)
Os primeiros seis termos são\(\{1, 4, 1, 16, 25, 2\}\).
Análise
Cada terceiro ponto no gráfico mostrado na Figura\(\PageIndex{4}\) se destaca dos dois pontos próximos. Isso ocorre porque a sequência foi definida por uma função por partes.
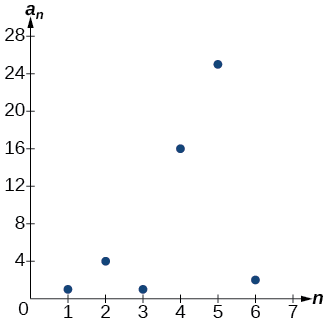
Figura\(\PageIndex{4}\)
Escreva os primeiros seis termos da sequência.
\(a_n=\begin{cases}2n^3 \text{ if } n\text{ is odd} \\ \dfrac{5n}{2} \text{ if } n \text{ is even}\end{cases}\)
- Resposta
-
Os primeiros seis termos são\(\{2, 5, 54, 10, 250, 15\}\).
Encontrando uma fórmula explícita
Até agora, recebemos a fórmula explícita e pedimos que encontrássemos vários termos da sequência. Às vezes, a fórmula explícita para o enésimo termo de uma sequência não é fornecida. Em vez disso, recebemos vários termos da sequência. Quando isso acontece, podemos trabalhar ao contrário para encontrar uma fórmula explícita dos primeiros termos de uma sequência. A chave para encontrar uma fórmula explícita é procurar um padrão nos termos. Lembre-se de que o padrão pode envolver termos alternados, fórmulas para numeradores, fórmulas para denominadores, expoentes ou bases.
- Procure um padrão entre os termos.
- Se os termos forem frações, procure um padrão separado entre os numeradores e denominadores.
- Procure um padrão entre os sinais dos termos.
- Escreva uma fórmula para\(a_n\) em termos de\(n\). Teste sua fórmula para\(n=1\)\(n=2\),\(n=3\) e.
Escreva uma fórmula explícita para o enésimo termo de cada sequência.
- \(\{−\dfrac{2}{11}, \dfrac{3}{13}, −\dfrac{4}{15}, \dfrac{5}{17}, −\dfrac{6}{19},…\}\)
- \(\{−\dfrac{2}{25}, −\dfrac{2}{125}, −\dfrac{2}{625}, −\dfrac{2}{3,125}, −\dfrac{2}{15,625},…\}\)
- \(\{e^4,e^5,e^6,e^7,e^8,…\}\)
Solução
Procure o padrão em cada sequência.
- Os termos alternam entre positivo e negativo. Podemos usar\({(−1)}^n\) para alternar os termos. O numerador pode ser representado por\(n+1\). O denominador pode ser representado por\(2n+9\).
\(a_n=\dfrac{{(−1)}^n(n+1)}{2n+9}\)
- Os termos são todos negativos.
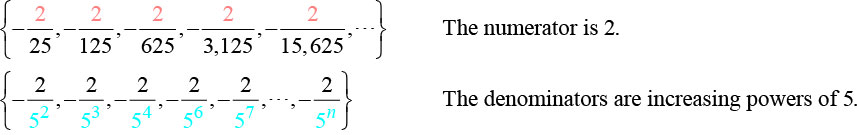
Então, sabemos que a fração é negativa, o numerador é\(2\) e o denominador pode ser representado por\(5n+1\).
\(a_n=−\dfrac{2}{5^{n+1}}\)
- Os termos são poderes de\(e\). Pois\(n=1\), o primeiro termo é\(e^4\) assim que o expoente deve ser\(n+3\).
\(a_n=e^{n+3}\)
Escreva uma fórmula explícita para o enésimo termo da sequência.
\(\{9,−81,729,−6,561,59,049,…\}\)
- Resposta
-
\(a_n={(−1)}^{n+1}9^n\)
Escreva uma fórmula explícita para o enésimo termo da sequência.
\(\{−34,−98,−2712,−8116,−24320,...\}\)
- Resposta
-
\(a_n=−\dfrac{3^n}{4n}\)
Escreva uma fórmula explícita para o enésimo termo da sequência.
\(\left \{ \dfrac{1}{e^2}, \dfrac{1}{e}, 1, e, e^2,... \right \}\)
- Resposta
-
\(a_n=e^{n−3}\)
Escrevendo os termos de uma sequência definida por uma fórmula recursiva
As sequências ocorrem naturalmente nos padrões de crescimento de conchas de nautilus, pinhas, galhos de árvores e muitas outras estruturas naturais. Podemos ver a sequência no arranjo de folhas ou galhos, o número de pétalas de uma flor ou o padrão das câmaras em uma concha de nautilus. Seu crescimento segue a sequência de Fibonacci, uma sequência famosa na qual cada termo pode ser encontrado adicionando os dois termos anteriores. Os números na sequência são\(1, 1, 2, 3, 5, 8, 13, 21, 34,….\) Outros exemplos do mundo natural que exibem a sequência de Fibonacci são o Calla Lily, que tem apenas uma pétala, a Susan de olhos pretos com\(13\) pétalas, e diferentes variedades de margaridas que podem ter\(21\) ou\(34\) pétalas.
Cada termo da sequência de Fibonacci depende dos termos que vêm antes dela. A sequência de Fibonacci não pode ser escrita facilmente usando uma fórmula explícita. Em vez disso, descrevemos a sequência usando uma fórmula recursiva, uma fórmula que define os termos de uma sequência usando termos anteriores.
Uma fórmula recursiva sempre tem duas partes: o valor de um termo inicial (ou termos) e uma equação definida\(a_n\) em termos de termos anteriores. Por exemplo, suponha que saibamos o seguinte:
\[\begin{align*} a_1 &= 3 \\ a_n &= 2a_{n−1}−1 , \text{ for }n≥2 \end{align*}\]
Podemos encontrar os termos subsequentes da sequência usando o primeiro termo.
\[\begin{align*} a_1 &= 3 \\ a_2 &= 2a_1−1=2(3)−1=5 \\ a_3 &= 2a_2−1=2(5)−1=9 \\ a_4 &= 2a_3−1=2(9)−1=17 \end{align*}\]
Portanto, os primeiros quatro termos da sequência são\(\{3, 5, 9, 17\}\).
A fórmula recursiva para a sequência de Fibonacci afirma os dois primeiros termos e define cada termo sucessivo como a soma dos dois termos anteriores.
\[\begin{align*}a_1 &= 1 \\ a_2 &= 1 \\ a_n &= a_{n−1}+a_{n−2} \text{, for }n≥3 \end{align*}\]
Para encontrar o décimo termo da sequência, por exemplo, precisaríamos adicionar o oitavo e o nono termos. Fomos informados anteriormente que o oitavo e o nono mandatos são\(21\) e\(34\), então
\(a_{10}=a_9+a_8=34+21=55\)
Uma fórmula recursiva é uma fórmula que define cada termo de uma sequência usando termos anteriores. As fórmulas recursivas devem sempre indicar o termo inicial, ou termos, da sequência.
Não. A sequência de Fibonacci define cada termo usando os dois termos anteriores, mas muitas fórmulas recursivas definem cada termo usando apenas um termo anterior. Essas sequências precisam apenas do primeiro termo para serem definidas.
- Identifique o termo inicial\(a_1\),, que é dado como parte da fórmula. Esse é o primeiro termo.
- Para encontrar o segundo termo,\(a_2\), substitua o termo inicial na fórmula para\(a_{n−1}\). Resolver.
- Para encontrar o terceiro termo\(a_3\), substitua o segundo termo na fórmula. Resolver.
- Repita até que você tenha resolvido o enésimo termo.
Escreva os primeiros cinco termos da sequência definida pela fórmula recursiva.
\[\begin{align*}a_1 &= 9 \\ a_n &= 3a_{n−1}−20 , \text{ for }n≥2 \end{align*}\]
Solução
O primeiro termo é dado na fórmula. Para cada termo subsequente,\(a_n−1\) substituímos pelo valor do termo anterior.
\(\begin{array}{ll} n=1 & a_1=9 \\ n=2 & a_2=3a_1−20=3(9)−20=27−20=7 \\ n=3 & a_3=3a_2−20=3(7)−20=21−20=1 \\ n=4 & a_4=3a_3−20=3(1)−20=3−20=−17 \\ n=5 & a_5=3a_4−20=3(−17)−20=−51−20=−71 \end{array}\)
Os primeiros cinco termos são\(\{9, 7, 1, –17, –71\}\). Veja a Figura\(\PageIndex{5}\).
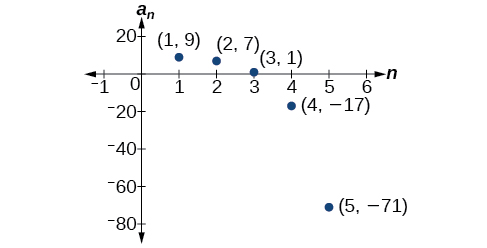
Figura\(\PageIndex{5}\)
Escreva os primeiros cinco termos da sequência definida pela fórmula recursiva.
\[\begin{align*} a_1 &= 2 \\ a_n &= 2a_{n−1}+1 , \text{ for }n≥2 \end{align*}\]
- Resposta
-
\(\{2, 5, 11, 23, 47\}\)
- Identifique o termo inicial\(a_1\),, que é dado como parte da fórmula.
- Identifique o segundo termo\(a_2\),, que é dado como parte da fórmula.
- Para encontrar o terceiro termo, substitua o termo inicial e o segundo termo na fórmula. Avalie.
- Repita até que você tenha avaliado o enésimo termo.
Escreva os primeiros seis termos da sequência definida pela fórmula recursiva.
\[\begin{align*} a_1 &=1 \\ a_2 &= 2 \\ a_n &= 3a_{n−1}+4a_{n−2} , \text{ for }n≥3 \end{align*}\]
Solução
Os dois primeiros termos são fornecidos. Para cada termo subsequente, substituímos\(a_{n−1}\) e\(a_{n−2}\) pelos valores dos dois termos anteriores.
\(\begin{array}{ll} n=3 & a_3=3a_2+4a_1=3(2)+4(1)=10 \\ n=4 & a_4=3a_3+4a_2=3(10)+4(2)=38 \\ n=5 & a_5=3a_4+4a_3=3(38)+4(10)=154 \\ n=6 & a_6=3a_5+4a_4=3(154)+4(38)=614 \end{array}\)
Os primeiros seis termos são\(\{1,2,10,38,154,614\}\). Veja a Figura\(\PageIndex{6}\).
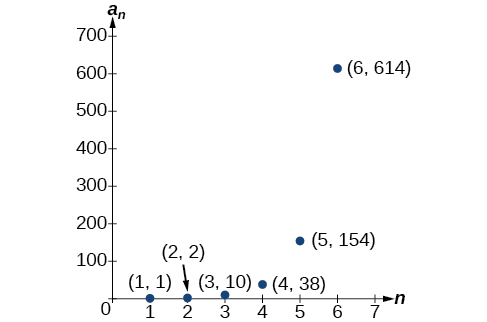
Figura\(\PageIndex{6}\)
Escreva os primeiros\(8\) termos da sequência definida pela fórmula recursiva.
\[\begin{align*}a_1 &= 0 \\ a_2 &= 1 \\ a_3 &= 1 \\ a_n &= \dfrac{a_{n−1}}{a_{n−2}}+a_{n−3} , \text{ for }n≥4 \end{align*}\]
- Resposta
-
\(\left \{0, 1, 1, 1, 2, 3, 52, 176 \right \}\).
Usando notação fatorial
As fórmulas para algumas sequências incluem produtos de números inteiros positivos consecutivos. \(n\)fatorial, escrito como\(n!\), é o produto dos números inteiros positivos\(1\) de\(n\) a. Por exemplo,
\[\begin{align*}4! &= 4⋅3⋅2⋅1=24 \\ 5! &= 5⋅4⋅3⋅2⋅1=120 \end{align*}\]
Um exemplo de fórmula contendo um fatorial é\(a_n=(n+1)!\). O sexto termo da sequência pode ser encontrado substituindo\(6\) por\(n\).
\(a_6=(6+1)!=7!=7·6·5·4·3·2·1=5040\)
O fatorial de qualquer número inteiro\(n\) é. Portanto, também\(n(n−1)!\) podemos pensar em\(5⋅4!\).\(5!\)
\(n\)fatorial é uma operação matemática que pode ser definida usando uma fórmula recursiva. O fatorial de\(n\), denotado\(n!\), é definido para um inteiro positivo\(n\) como:
\[\begin{align} 0! &= 1 \\ 1! &= 1 \\ n! &= n(n−1)(n−2)⋯(2)(1), \text{ for }n≥2 \end{align}\]
O caso especial\(0!\) é definido como\(0!=1\).
Não. Os fatoriais aumentam muito rapidamente — mais rápido do que até mesmo as funções exponenciais! Quando a saída ficar muito grande para a calculadora, ela não poderá calcular o fatorial.
Escreva os primeiros cinco termos da sequência definida pela fórmula explícita\(a_n=\dfrac{5n}{(n+2)!}\).
Solução
Substitua\(n=1\)\(n=2\),, e assim por diante na fórmula.
\(\begin{array}{ll} n=1 & a_1=\dfrac{5(1)}{(1+2)!}=\dfrac{5}{3!}=\dfrac{5}{3·2·1}=\dfrac{5}{6} \\ n=2 & a_2=\dfrac{5(2)}{(2+2)!}=\dfrac{10}{4!}=\dfrac{10}{4·3·2·1}=\dfrac{5}{12} \\ n=3 & a_3=\dfrac{5(3)}{(3+2)!}=\dfrac{15}{5!}=\dfrac{15}{5·4·3·2·1}=\dfrac{1}{8} \\ n=4 & a_4=\dfrac{5(4)}{(4+2)!}=\dfrac{20}{6!}=\dfrac{20}{6·5·4·3·2·1}=\dfrac{1}{36} \\ n=5 & a_5=\dfrac{5(5)}{(5+2)!}=\dfrac{25}{7!}=\dfrac{25}{7·6·5·4·3·2·1}=\dfrac{5}{1,008} \end{array}\)
Os primeiros cinco termos são\(\left \{\dfrac{5}{6}, \dfrac{5}{12}, \dfrac{1}{8}, \dfrac{1}{36}, \dfrac{5}{1,008} \right \}\).
Análise
A figura\(\PageIndex{7}\) mostra o gráfico da sequência. Observe que, como os fatoriais crescem muito rapidamente, a presença do termo fatorial no denominador faz com que o denominador se torne muito maior do que o numerador à medida que nn aumenta. Isso significa que o quociente fica menor e, como mostra o gráfico dos termos, os termos estão diminuindo e se aproximando de zero.
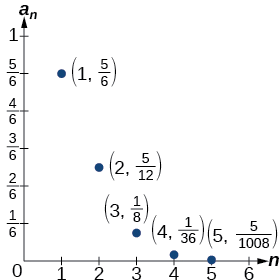
Figura\(\PageIndex{7}\)
Escreva os primeiros cinco termos da sequência definida pela fórmula explícita\(a_n=\dfrac{(n+1)!}{2n}\).
- Resposta
-
Os primeiros cinco termos são\(\left \{1, \dfrac{3}{2}, 4, 15, 72 \right \}\).
Acesse este recurso on-line para obter instruções e práticas adicionais com sequências.
Equações-chave
| Fórmula para um fatorial |
\(0!=1\) \(1!=1\) \(n!=n(n−1)(n−2)⋯(2)(1)\), para\(n≥2\) |
Conceitos-chave
- Uma sequência é uma lista de números, chamados termos, escritos em uma ordem específica.
- As fórmulas explícitas definem cada termo de uma sequência usando a posição do termo. Veja exemplo\(\PageIndex{1}\)\(\PageIndex{2}\), exemplo e exemplo\(\PageIndex{3}\).
- Uma fórmula explícita para o décimo enésimo termo de uma sequência pode ser escrita analisando o padrão de vários termos. Veja o exemplo\(\PageIndex{4}\).
- As fórmulas recursivas definem cada termo de uma sequência usando termos anteriores.
- As fórmulas recursivas devem indicar o termo inicial, ou termos, de uma sequência.
- Um conjunto de termos pode ser escrito usando uma fórmula recursiva. Veja o exemplo\(\PageIndex{5}\) e o exemplo\(\PageIndex{6}\).
- Um fatorial é uma operação matemática que pode ser definida recursivamente.
- O fatorial de\(n\) é o produto de todos os números inteiros\(1\) de\(n\) a. Veja o exemplo\(\PageIndex{7}\).


